思维导图在整体性教学中的应用实践
⦿ 江苏省靖江市第一高级中学 闻 君
数学是一门逻辑性较强的学科,但受学生认知水平、思维能力等因素的影响,这些逻辑连贯的数学知识可能分散于不同的章节中,因此数学教学要注重整体性.在日常教学中,教师应从整体视角出发,有意识地引导学生将相似或相关的知识联系起来,构建前后一致、逻辑连贯的知识体系,提高灵活应用知识解决问题的能力.如何开展整体性教学一直是高中数学教学的重要课题.笔者认为,在课堂教学中融入思维导图,有利于整体性教学的开展.笔者以“数列的前n项和”为例,谈谈具体的心得体会,请指正.
1 教学实录
1.1 巧借思维导图,促进知识整体把握
师:回顾数列相关知识,对于数列我们经历了怎样的学习历程?
生1:从一般数列出发,到等差数列、等比数列,再回到一般数列.
师:很好,这里面蕴含了一般与特殊的数学思想方法.我们可以从哪几个角度研究一般数列呢?
生2:数列的通项及其前n项和.
师:对于通项,是如何研究的?(学生一时不知如何回答.)
师:结合实例想一想,我们是如何研究数列通项问题的?(教师用PPT给出数列让学生观察、思考.)
(1)已知a1=2,an+1-an=2n+1(n∈N*),求数列{an}的通项公式.
(2)已知{an}满足a1=1,an+1=2an+1,求这个数列的通项公式an.
学生独立求解,教师展示学生的解题过程(略).
师:对于问题(1),你是如何想到用累加法求解的呢?
生3:发现该递推关系与等差数列的定义类似,所以解题时联想到等差数列通项的推导方法,利用累加法得到了答案.
师:很好.对于问题(2),你们有什么想说的吗?
生4:将递推关系变形得an+1+1=2(an+1),又an+1=2≠0,所以问题可以转化为等比数列{an+1}的通项问题.
师:很好.结合已有经验和具体实例说说,求一般数列通项的核心思想是什么?
生5:在求一般数列的通项时,或类比等差、等比数列通项的推导方法,或将其转化为等差、等比数列.
学生回答问题后,教师带领学生进一步回顾研究一般数列的基本内容和基本思想方法,然后给出如图1所示的思维导图.
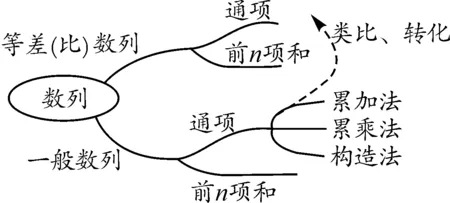
图1
师:总结得非常好!对于一般数列的通项,我们可以用“类比”与“转化”的思想来研究,那么对于一般数列的前n项和,是否也能用这两种思想来研究呢?
1.2 巧借思维导图,提高学生实践能力
师:为了检验“类比”与“转化”是否通用,我们看一个具体实例.(教师用PPT出示例题.)
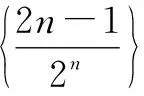
问题给出后,教师让学生独立求解,教师巡视,很多学生无从下手.
师:数列的通项是什么?

师:该数列通项有何特征?
生6:它是等差数列通项与等比数列通项之积.
师:结合这一发现,你有什么想法?
生7:感觉也可以像研究一般数列的通项一样,借助研究等差、等比数列前n项和的方法来研究它.
师:不错的思路,大家试一试,看看有什么发现.
(教师继续让学生独立思考.)
生8:直接转化是不行的,因为例1的通项无法转化为等差、等比数列的通项.
生9:我从类比的角度出发,先与等差数列相类比,发现应用倒序相加法不能解决问题,其他方法还没有来得及尝试.
师:分析得非常有道理.大家不妨用错位相减法试一试,看看你有什么发现?
在教师的启发和指导下,学生利用错位相减法得到该数列的前n项和.教师投影展示生10的解答过程:

师:根据这一发现,你能得到一般结论吗?
生11:若一般数列的通项形如anbn,其中{an}是等差数列,{bn}是等比数列,则求一般数列的前n项和时,可以使用错位相减法.
师:很好,这样通过与等比数列求和相类比,得到了这个一般数列的求和方法.
师:若通项是等差数列与等比数列对应项和的形式,则只需分别计算等差、等比数列的前n项和,然后将二者相加得到结果,我们称该方法为分组求和法.
这样从学生已有经验出发,学生理解并掌握一般数列求和的方法后,教师提供时间让学生反思回顾,并通过师生互动交流得到如图2所示的思维导图,以此借助思维导图加深对基本思想方法的理解,增强学生解题信心.

图2
1.3 巧借思维导图,培养学生整体意识
师:本节课我们主要研究了哪些内容?你有哪些收获?请用思维导图归纳总结相关内容.
教师预留时间让学生反思回顾,然后尝试利用思维导图进行归纳总结,学生得到草图后,教师鼓励学生进行组内交流,以此通过生生合作逐步完善个体的认知结构.教师展示各组的交流结果后,又对其作进一步优化,从而得到如图3所示的思维导图.
2 教后反思
周知,数学知识之间存在着千丝万缕的联系,若教学中不能通过有效的方式将这些知识联系起来,那么将很容易出现遗忘的情况.这样学生在面对一些综合性的题目时往往会感觉无从下手,直接影响解题效果.思维导图在整合知识、帮助记忆、发散思维等方面发挥着重要作用,因此教学中应充分发挥思维导图的优势,将知识、思想方法等有效地联系起来,让学生逐步形成整体观,提高学习效率.
在本课教学中,教师从学生已经掌握的一般数列的通项入手,通过问题的解决引导学生提炼转化和类比思想方法.在此基础上,教师巧妙地设计问题,引导学生将研究一般数列通项的思想方法迁移至一般数列求和的推导中,实现由等差、等比数列求和到一般数列求和的推广,充分展示各知识点之间的联系,逐步培养学生整体意识.另外,在各个教学环节中,教师引导学生用思维导图进行归纳总结,帮助学生生成数列的知识体系.相信在思维导图的指引下,学生在研究一般数列的问题时,可以快速找到思考方向,形成解题策略,提升解题信心.
总之,在整体性教学中,教师要适时地引入思维导图,有意识地指导学生利用思维导图将相关的知识联系起来,帮助学生更好地理解知识,形成完善的知识体系,提高分析问题和解决问题的能力.

