基于深度强化学习的通信动态抗干扰决策模型

陈帅明

摘要：随着通信技术发展，频谱资源有限，抗干扰能力不足，已广泛影响通信质量和可靠性。为提升通信可靠性，将强化学习与VHF动态抗干扰决策相结合，综合考虑通信信道切换和发射功率控制。提出基于深度强化学习算法的VHF动态抗干扰决策模型，使用仿真分析验证强化学习决策模型的有效性。实验结果表明，深度强化学习决策模型的抗干扰性能、收敛速度均优于传统的强化学习算法，具有较高的吞吐量和较低的功耗。

关键词：深度强化学习；VHF；动态抗干扰；决策模型

中图分类号：TP3    文献标识码：A

文章编号：1009-3044（2024）09-0089-04

开放科学（资源服务）标识码（OSID）

0  引言

随着通信技术发展，民航、应急通信等领域VHF（Very High Frequency，VHF）无线通信系统抗干扰要求更加严格。GWON Y等基于强化Q学习技术提出了最佳信道访问策略[1]。SLIMENI F在认知无线网络场景中提出基于策略同步Q学习的信道分配策略[2]。HANAWAL M K等提出的零和博弈研究了跳频和传输速率控制，但只分析了反应式扫频干扰方式，对多种干扰环境并不适用[3]。同时，这些算法都只是利用信道切换来规避干扰，频繁切换信道会增加系统成本，并不能带来整体性能的提升。

对此，提出基于深度强化学习（Deep Reinforcement Learning，DRL）的VHF动态抗干扰决策模型，在多用户场景下同时进行信道选择和功率分配，将问题建模为Stackelberg博弈过程，既考虑通信信道的访问与发射功率控制，又考虑快速适应环境变化的算法收敛速度。

1  问题分析与建模

1.1  系统模型

VHF无线通信环境中，发射机向接收机发送信号，成功接收后接收机发回ACK。发射控制在发射机侧，代理感知频谱，指导发射机选择通信频率和通信功率，并根据接收ACK和频谱调整通信决策。

在时间t，发射机发射的信号功率为[pt，pt∈Ps，Ps]为发射机功率设置数值集合[card（Ps）=n]，假设发射机的中心频率为[ft，ft∈Fs，Fs]为发射机中心频率设置数值集合[card（Fs）=m]。设置发射信号中频带宽为[bs]，假设在时间t，干扰信号频带为[bj]，干扰信号频率的中心频率为[fjt]，干扰信号的功率谱密度[Jt（f）]。发射机至接收机的信道增益为[gs]，干扰信道至发射机的信道增益为[gj]，且环境噪声的功率谱密度为[n（f）]。那么接收机所感知到的信噪比可以表示为：

[β（ft，pt）=gsptft-bs2ft+bs2（n（f）+gj（f-fjt））]  （1）

设[βth]为信号成功传输的门限值，那么表述成功通信功能的表达式为：

[u（ft，pt）=1   β（ft，pt≥βth）0   β（ft，pt<βth）]    （2）

因此，如果[u（ft，pt）=1]，接收机会向发射机发回ACK信号。对于归一化的数据吞吐量，用一次迭代表示N次通信，可以计算出归一化的数据吞吐量为：

[U=n=1n=Nu（fn，pn）N]    （3）

其中[fn]为时刻n选择的频率，[pn]为时刻n选择的功率。那么归一化的能量消耗V就可以表示为：

[V=n=1n=NpnNph]     （4）

其中[ph]为功率集合[Ps]的最大功率。那么每个信号E使用的归一化功率可以表示为：

[E=UV]       （5）

1.2  问题模型

算法的优化目标是确保在每次通信中，发射机能够选择正确的通信信道，并达到最小的能耗。优化目标为：

[θ=min（β（f，p）），  s.t.β（f，p）≥βth]  （6）

将在无线环境中选择通信中心频率和功率的优化问题建模为一个由4元组[（S，A，R，P）]描述的马尔可夫决策过程（Markov decision process，MDP） [4]。在时间t的代理感应频谱为[St∈S]，T是用来决定频率和通信功率的时间段[at∈A]。在信号发送以后，我们得到了带有奖励信息[rt∈R]的ACK确认信息。用P作为过渡概率，当T足够大时，可证明该抗干扰决策过程是一个马尔可夫决策过程，该过程中的转移矩阵可定义为：

[P（ST+1|ST，ST-1，...，ST-∞）]

[=P（sT+1，sT，...，st-T+2|sT，sT-1，...，sT-∞）]

[=P（st+1|st，st-1，...，st-∞）]        （7）

假設只需用限制历史信息来预测下一时刻的状态，且需求小于K。这意味着在决定[at]确认之后，[St+1]独立于[Sk，Sk-1，...，Sk-∞]，抗干扰决定已经确认，因此传输矩阵可以写为：

[P（St+1|St，St-1，...，St-∞，at）]

[=P（st+1|st-T+1，at）]

[=P（St+1|St，at）]      （8）

因此，该过程是一个马尔可夫决策过程（MDP） ，使用深度强化学习（DRL） 算法来处理MDP中的最优信道和功率决策问题。

2  基于深度强化学习决策模型构建

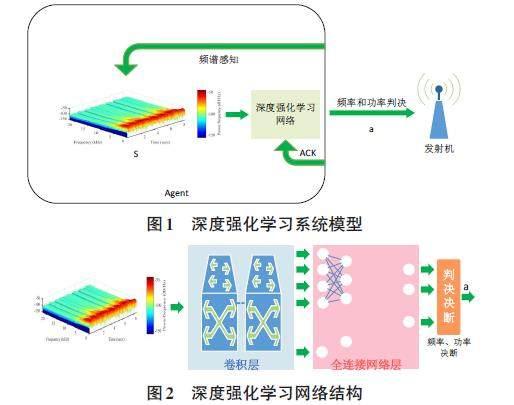
DRL结合了深度学习的特征来提取特征和强化学习来处理未知环境下的任务，需要考虑环境中的多元变量[5]，如图1和图2所示。

DRL网络的输入信息是S，称为频谱瀑布。S通过信号能量在以[?f]的频率为间隔感知[St]的过程中产生，即[st=st，f0，st，f0+?f，...st，f]，对应到[?t]时间为[St=St，St-?t，...，St-T]，其中[f0]是信号能量检测的起始频率，f是感知过程的结束频率，T是频谱瀑布的时间长度，[St，f0]的计算过程如下：

[St，f0=10logf0f0+?f（gsU（f）+gjJ（f）+n（f））df）] （9）

由于S是时域叠加频域叠加能量域的三维信息，所以状态空间很大。在深度强化学习网络的设计中，使用卷积层提取频谱中的信息，利用全连接网络对提取的频谱信息进行合成。DRL网络的输出由信道频率和功率联合决定，网络设计结构如图3所示。

DRL网络的输出是传输功率和传输信道[at=（ft，pt），at∈A]共同的传输动作，其中A包含的动作数量为[n×m]，因为集合[（Ps）=n]，集合[（Fs）=m]，如图3中所示。接收机以ACK信号的形式送回通信决断[at]的反馈[rt]，[rt]的计算过程如下：

[r（at）=u（ft，pt）×（1-c（pt-plph-pl））] （10）

其中[ph]是集合[Ps]中的最大值，[ph=supPs]，[pl]是集合[Ps]中的最小值，[pl=infPs]。[c∈（0，1）]是一个决策因子。各个动作对应的目标函数定义为：

[η=（r（a）+λmaxQ（S'，a';θi-1））] （11）

其中[Q（S'，a';θi-1）]是DRL的网络函数，λ是学习率，S'是执行a之后的下一状态，[θi-1]是第i-1次迭代中的网络权重。根据定义的目标函数，损耗函数可定义为：

[L（θi）=[Q（S，a;θi）-ηi]2] （12）

基于最小化损失函数L，用梯度下降算法优化网络权值θ。重放存储器是用来保存训练数据的数据集，并且重放存储器M的大小为m。M中存储的数据满足先进先出（FIFO） 的原理。例如，在DRL的第k次迭代中，[M=ek，ek-1，...，ek-m+1]，而[ek=（Sk，ak，ηk，Sk+1）].最终，在算法1中呈现出了提出的学习算法。需要注意的是，i不同于t。t是运行算法的时间，但i是更新DRL网络的迭代次数。

3  仿真分析验证

3.1  模拟仿真结果和分析

在模拟仿真中，发射机、接收机和干扰机都是在100MHz～110MHz的频谱环境中。其中发射机以100kHz的间隔每1ms进行一次全波段感知，每5ms发送一次信号。发射功率分别选择30dbm、35dbm、40dbm，发射机的信号带宽为2MHz。中心频率[f∈101，103，105，107，109]，这意味着发射机具有[3×5=15]组动作。发射机的解调阈值为10db。对于代理机，决策因子设置为c=0.4，学习速率λ=0.2，代理机每1ms执行一次全频带感知。通道增益[gj=0.01，gs=0.01]。干扰信号和传输信号都是提升的余弦波形和偏离因子[η=0.4]。一次迭代的N是100。几个模拟中考虑干扰模式：

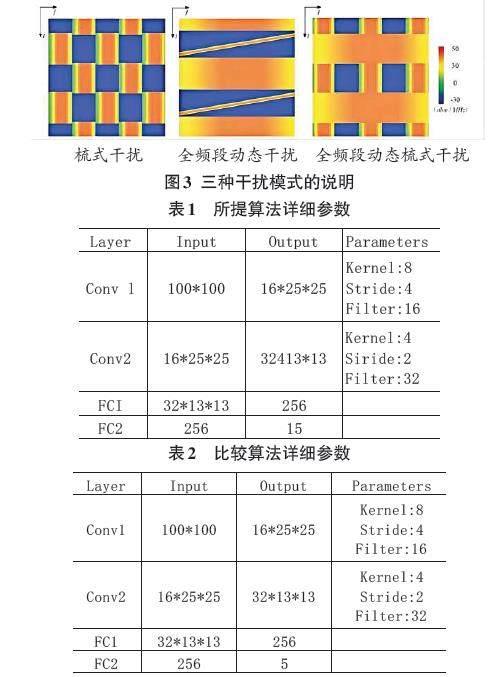
1） 动态梳状干扰：干扰信号中心频率从101MHz、105MHz、109MHz至103MHz、107MHz。干扰频带为2MHz，干扰功率为40dbm。

2） 扫描、全波段动态干扰：每25 ms重复发生全波段干扰。这个扫描速度为0.4GHz/s，干扰功率为50dbm。

3） 梳式和全频段动态干扰：干扰方式从梳式干扰（干扰信号中心频率为101MHz、105MHz、109MHz）到每25ms全频段干扰，干扰功率为50dbm。

在图4中，结果表明在传输用户的大功率信号时，干扰信号完全可以忽略。因此，高功率方案可以达到最大吞吐量，但能耗也是最高的。所提出和比较的算法需要训练来提高吞吐量。可以看出，该算法经过40次迭代后，可达到最大吞吐量的95%。从图5中可以看出，该算法可以在40次迭代中降低接近最低点的能量成本。在图6中虽然总是有一个频率可以避免干扰信号，但该算法可以正确地选择低功率频率，保持功率以低成本运行，如在40次迭代后保持低功率方案。

4  结束语

根据研究，深度强化学习在动态抗干扰系统中具有优势，能够自动学习并调整策略，实时调整系统的抗干扰策略，通过与环境的交互，不断尝试不同的策略，并通过奖励信号来评估策略的好坏。

本文研究了抗干扰通信中的功率和通信频率的优化问题，将该问题表述为马尔可夫决策过程（MDP） ，提出了基于深度强化学习（DRL） 的抗干扰算法决策模型，该算法可以同时切换频率和功率。仿真结果表明，该算法在降低能耗的同时，实现了高吞吐量。

参考文献：

[1] GWON Y，DASTANGOO S，FOSSA C，et al.Competing Mobile Network Game：embracing antijamming and jamming strategies with reinforcement learning[C]//2013 IEEE Conference on Communications and Network Security （CNS）.October 14-16，2013.National Harbor，MD，USA.IEEE，2013：28-36.

[2] SLIMENI F，SCHEERS B，CHTOUROU Z，et al.Jamming mitigation in cognitive radio networks using a modified Q-learning algorithm[C]//2015 International Conference on Military Communications and Information Systems （ICMCIS）.May 18-19，2015.Cracow，Poland.IEEE，2015：1-7.

[3] HANAWAL M K，ABDEL-RAHMAN M J，KRUNZ M.Joint adaptation of frequency hopping and transmission rate for anti-jamming wireless systems[J].IEEE Transactions on Mobile Computing，2016，15（9）：2247-2259.

[4] 李芳，熊俊，趙肖迪，等.基于快速强化学习的无线通信干扰规避策略[J].电子与信息学报，2022，44（11）：3842-3849.

[5] 郭振焱.复杂对抗环境下的通信抗干扰策略生成方法[D].成都：电子科技大学，2022.

【通联编辑：朱宝贵】