多态场景下考虑出行链重构的电动汽车多目标协同优化调度

朱永胜，孙 贤，谢晓峰，丁同奎，巫付专，史志鹏

（1.中原工学院电子信息学院，河南省郑州市 450007；2.国网郑州供电公司，河南省郑州市 450052）

0 引言

近年来，随着中国电动汽车（electric vehicle，EV）保有量的迅速上升，EV 集群作为分布式储能资源，削峰填谷和节能减排的能力逐渐增强［1-4］。但是，用户充电选择上的主观性导致了EV 的时空负荷具有较大的突变性，并对原有的充放电调度计划造成破坏［5］。因此，尽可能充分考虑EV 充放电调度过程中的用户主观性，已经成为了亟待解决的问题。

目前的研究工作主要以EV 确定的出行行为作为基础进行充放电调度。文献［6-10］模拟常态下EV 负荷需求的时空分布，得到EV 参与能量互动的稳定时长，并设定不同调度目标对EV 进行充放电调度。文献［11］建立了出行修正模型，描述EV 受用户主观性的影响，行驶状态中的目的地和入网时间改变的过程。文献［12］提出随机停靠模型，模拟EV 在出行过程中的自主停靠行为，增加了EV 入网时间的不确定性。上述文献仅考虑EV 在充电前的不确定性，忽略了用户主观性对EV 充放电过程的影响。

文献［13］采用鲁棒优化方法，优化某时段内由于EV 异常进入或离开负荷聚合商所造成的异常功率波动，确保每辆EV 的充电安全。该文献并未考虑到用户实际的出行需求，仅提供了异常功率波动的解决方案。文献［14］基于EV 行驶路径的不确定性，建立了EV 在不同使用场景下的自适应充放电策略。文献［15］对每个充电时段进行两阶段分析，预测未来时段内不确定的充电需求。文献［16］通过信息间隙决策理论讨论了EV 接入负荷聚合商时刻的不确定性。文献［14-16］虽然考虑到EV 使用的不确定性，但仍然基于确定的负荷需求区间对EV的充放电进行预测及调度。文献［17］虽然提出了EV 在某置信水平下的负荷区间预测方法，但没有进一步讨论EV 的充电过程在任意时刻均可中断的可能性，以及特殊时段内用户对充电功率的最低要求。

文献［18-20］讨论了极端条件下EV 参与负荷恢复的过程。文献［18-19］讨论了以应急发电车辆为供电主体，向区域电网进行供电，但并未充分发掘EV 作为分布式储能资源的潜力。文献［20］讨论了在极端供电状态下，EV 集群作为不可中断电源向区域电网负荷供电的潜力，但忽略了用户的出行需求。文献［21-22］将EV 集群在不同时段视为容量不同的储能单元，以此消纳各时段多余的电力供给，但忽略了EV 集群可突变的储能潜力。

综上所述，目前对常态下EV 的不确定性研究集中在以负荷聚合商为调度主体，考虑EV 负荷区间的不确定性，或者将EV 个体视为具有最短充电时长的能量互动单元，对EV 个体进行充放电调度。未充分考虑常态下，由于用户主观性导致的充放电调度计划的异常中断、用户对充放电功率的实际需求以及用户出行链的改变对后续充放电调度计划的影响。当极端状态发生时，对极端状态下的研究工作仅考虑极端状态前EV 的出行模型，EV 通常被视为储能资源稳定的能量供给和消纳单元，未充分考虑用户本身的出行需求。

据此，本文提出多态场景下考虑用户出行链重构的EV 电力调度策略。首先，模拟用户自身充电意愿对充电选择的影响，提出用户充电意愿模型；然后，提出出行链重构模型，模拟用户在突发事件影响下出行链改变的过程；其次，提出多态场景下储能站协同EV 的调度策略；最后，综合以上模型，以用户经济性和负荷需求稳定性为目标，构建日前、实时双阶段调度模型，对EV 进行充放电调度。通过区域电网进行仿真，验证了所提模型的有效性。

1 EV 出行行为模型

1.1 EV 分类

考虑到用户充电需求差异，本文将EV 分为3 类:1）刚性EV，此类EV 以当前节点的最大充电功率进行充电，不参与调度；2）慢充EV，此类EV 是参与充放电调度的主体，并以不大于节点的最大慢充功率进行充电，本文假设该类EV 在停驻时会与充电桩相连［23］；3）快充EV，进行充放电调度时，需要首先满足用户的出行需求。

任意一辆EV 的状态可以用一维矩阵表示:

式中:D为表示EV 是否参与调度的0-1 变量，值为0、1 分别表示不参与调度和参与调度；G为EV 充放电类型，值为-1、1、2 和3 分别表示维持原有的充放电计划、调度计划改变、以最大慢充功率充电和以最大快充功率充电；Cn，t为第n辆EV 在t时 段的充放电标识，处于放电状态时，放电标识C为1、充电标识C为0，而处于充电状态 时C为1、C为0，其余 状 态 时C和C均为0；Sn，t为 第n辆EV 在t时段的电量；Tin、Tout分别为EV 的入网时段、离网时段；Eh为二进制数，值为1 和0 分别表示出行链重构事件发生和不发生；Ec为出行链重构事件类型；Et为出行链重构事件发生的实际时刻；i和U分别表示第几次出行和总的出行次数；S为第n辆EV 的里程焦虑值；L为EV 第i次出行中路段节点的有序集合，L={LS，LM，LD，LF}，其中，LS、LM、LD和LF分别为当前所在节点、中间节点、原出行链目的地节点和距离最近的快充站节点。

1.2 出行链重构事件

EV 处于行驶状态中发生出行链重构事件时，需要对该段行程的目的地和行驶路径进行调整。EV 处于停驻状态时，本文提出4 种出行链重构事件模拟出行链重构对停驻阶段的影响，如图1 所示。

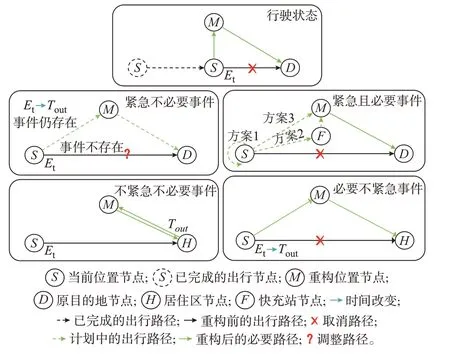
图1 出行链重构事件示意图Fig.1 Schematic diagram of trip chain reconstruction events

本文对停驻状态下的EV 出行链重构事件分类如下:1）紧急且必要事件，往往时效性较短，但重要性较强，需要用户即刻处理；2）紧急不必要事件，时效性较短，重要性较低，用户需要抉择是否进行处理；3）必要不紧急事件，时效性较长，对用户来讲重要性较强，本文设定用户选择在原出行链的基础上，以最短出行距离完成该事件；4）不紧急不必要事件，时效性较长，本文设定用户回家之后再处理。

1.3 EV 出行链模型

本文采用交通节点和配电网节点一一对应的方式刻画路-网耦合关系图，如附录A 图A1、图A2 和表A1 所示。本文依据文献［24］的出行链理论以及NHTS2017 数据［25］，构建EV 时空分布模型，如附录A 图A3 所 示。

EV 在不同区域停驻时长具有不同形式的分布函数，本文将城市区域划分为三大类:居民区（H）、工作区（W）和商业区域（O）。

居民区（H）停驻时长为:

工作区（W）停驻时长为:

商业区（O）停驻时长为:

式中:T为当前时刻；ΔTP为T时刻EV 进行停驻的停驻时长。

通过式（5）描述气温对电池的影响。

式 中:Ht为t时 段 的 气 温；Qn，t和QO，n，t分 别 为 第n辆EV 在t时段的实际电池容量和电池原本容量。通过Dijkstra 算法以最短用时规划行驶路径。

1.4 EV 用户充电意愿模型

当EV 电量低于里程焦虑值时，EV 用户会选择立即前往充电［26-29］；当EV 电量高于里程焦虑值但低于充电意愿阈值时，用户会衡量能否到达该行驶阶段的目的地，如附录A 图A4 所示。

当用户判断该电量能够抵达该行驶阶段的目的地时，用户会下调充电意愿阈值并继续行驶。当用户判断不能到达目的地时，则选择距当前位置节点最近的充电节点进行充电。

式 中:KLS，LD，n为 第n辆EV 在 当 前 位 置 节 点LS距 本段路程的终点LD的距离；α为第n辆EV 在该路段出行过程中的充电意愿系数；Ki，n为第n辆EV 在第i次出行中的路径长度；Sax，n为第n辆EV 用户的原始 充 电 意 愿；S为 第n辆EV 用 户 调 整 之 后 的 充电意愿阈值。

2 EV 出行链重构

EV 发生出行链重构事件，并且EV 按照重构后的出行链行驶时，EV 的出行链应当得到如下调整:

式 中:Un为 第n辆EV 总 的 出 行 次 数；Pn，Et～96和Et～96分别为EV 在Et到第96 个时段出行链重构前后 的 功 率；Scon、S′con分 别 为EV 在Et到 第96 个 时 段出 行链重构前、后的路程约束；Eu，un，h为判断是否出行 的 变 量，Eu，un，h为0 时 表 示 不 出 行，为1 时 表 示 出行。

2.1 行驶状态

当EV 行驶过程中发生出行链重构事件时，需要对EV 出行的目的地和路径进行调整:

式 中:LD，i为 第i次 出 行 中 原 来 的 目 的 地；ΔTLS，LD表示从LS到LD所消耗的时间；vˉ为平均速度；δ为交通拥堵系数，如附录A 表A2 所示表示向上取整。

2.2 停驻状态

2.2.1 紧急且必要事件

这类事件时效性短、重要性强，需要用户迅速前往目的地。因此，需要EV 的电量能够满足接下来的行程或能够到达距离目的地最近的充电站。本文设计了3 种充电方案，力求在此类事件发生的情况下，保证用户能在最短时间内到达目的地。下文将此类事件命名为事件1。

1）EV 在当前所在地LS以最大慢充功率充电，使得EV 在出发时的电量大于LS到LM的行程消耗量S与LM到LD的 行 程 消 耗 量S之 和，再 出发至出行链重构事件发生位置LM，最后到达原定出行链目的地LD。

2）EV 在当前所在地LS前往距离最近的快充站节点LF进行快充，并使得充电结束后的电量大于LF到LM的 行 程 消 耗 量S与S之 和，再 出 发 至LM，最后到达LD。

3）用户的电量能够到达LM，并且在该目的地的停驻阶段以最大慢充功率充电时，其再次出发的电量能够满足S。

在事件1 中，需要用户能够在最短时间内到达目的地，本文设定该类事件发生后忽略用户充电意愿阈值。当该类事件发生时，EV 的状态为:

式中:Scon的下标表示发生出行链重构事件前，满足该 段 路 程 电 量 约 束 的 起 止 节 点；Tu，n，1、Tu，n，2和Tu，n，3为3 种充电方案到达LM的时间；P为第n辆EV 的充放电功率，上标c 和d 分别为充电和放电标识，上标s和f 分别为慢充和快充标识，上标max 为最大功率标识；Pc，max，fn和Pc，max，sn分别为第n辆EV 在当前节点的最大快充功率和最大慢充功率；Sn，Et为第n辆EV在Et时段的电量；Tout和Tin的数字下标为该次事件的入网和离网次数；表示向下取整；S′n，Tout表示出行链重构后，第n辆EV 在离网时间Tout之后的行程约 束；ΔTLS，LF，LM表 示 从LS到LF再 到LM所 消 耗 的时间。

当用户完成紧急且必要事件后，用户的充电意愿和里程焦虑对EV 充放电调度的影响应当重新纳入考虑范围。

2.2.2 紧急不必要事件

紧急不必要事件对用户的影响通常较小。例如，用户偶然得知某超市在某时段内打折等，用户综合考虑成本和收益后决定是否出行。

本文设定此类事件发生后，用户需要判断在该停驻时段结束并到达目的地时，该事件是否仍然存在，如果存在则在该停驻时段结束后立即出行；如果该事件不存在，但用户选择在当前所在节点立即出发，并且抵达LM后该事件仍然存在，则用户选择对充放电计划调整后完成该事件；如果都不满足则仍然按照原出行链进行出行过程。下文将此类事件命名为事件2。

式 中:TEu，un为 该 事 件 的 持 续 时 间；max为 第n辆EV在当前节点的最大充电功率，其中，Tout，1同式（12）。

2.2.3 必要不紧急事件和不紧急不必要事件

必要不紧急事件对用户重要性较强，但是实施时间可以自由确定，如约会、团建和健身等，用户在这类事件发生时会选择在回家之前，以最短行程距离完成该事件。因此，对Et之后所有时段的充放电调度计划进行调整:

不紧急不必要事件对用户日间的生活和工作影响很小。例如，临时起意的夜间旅行、夜间临时值班等，用户会在回家之后再决定是否出门。

式中:TLH～96为用户回家后至24:00 的任意时刻。

当必要不紧急事件和不紧急不必要事件发生时，EV 服从优化调度。在优化调度过程中EV 除一般约束条件外，不存在某时段内强制性的充电功率限制，并且执行两种事件的具体时间通常距当前时刻较远，经过优化后对负荷需求影响较小。因此，下文将这两种事件统称为事件3，并一同分析。

3 多态能源系统框架

本文采用火电机组、风电机组、储能站和EV 分布式能源共同组成能源系统。其中，火电机组、风电机组作为常规供电单元［30］。常态下，通过对EV 的充放电调度实现削峰填谷，储能站作为储能设备协同EV 参与能量互动［31］；极端状态下，储能站和EV应当承担起供电或消纳任务:

1）作为断电状态下的后备能源。当常规供电单元因不可抗力而无法正常供电时，储能站作为应急供电单元协同EV 向一级负荷和二级负荷供电。

2）作为极端状态下的消纳单元。由于风电等新能源机组发电的不确定性，储能站和EV 作为容量可观的负荷消纳端，能够消耗多余的电量。

为此，本文设置储能站常态下的上限临界值为80%，剩余容量作为消纳负荷容量，设置储能站常态下的下限临界值为20%，作为备用能源。

常态下，当储能站在t时段存储的电量高于上限临界值时，则在t+1 时段需要由储能站作为供电主体，风电机组出力由电转气设备消纳。

当储能站在t时段存储的电量低于上限临界值并高于下限临界值时，则在t+1 时段由风电机组、储能站和火电机组共同参与供电。

当储能站在t时段的存储的电量低于下限临界值时，则在t+1 时段中储能站不参与供电，仅由风电机组和火电机组供电，风电机组产生的多余电力优先由储能站存储。能源系统框架图如附录A 图A5 所示。

各机组在常态条件下的出力如下。

1）储能站机组:

式 中:Ps，t为t时 段 内 储 能 站 的 出 力；Ss，t为t时 段 内 储能站的电量；M为储能站容量上限；Pw，t为t时段内风电机组出力；Po，t为优化之后t时段的负荷需求；Pb，t为t时 段 的 基 础 负 荷；Pcn，t和Pdn，t分 别 为 第n辆EV在t时段的充电功率和放电功率；N为EV 总数。

2）火电机组用于补足风力和储能站发电未满足的负荷需求:

式 中:Pf，t为t时 段 内 火 电 机 组 出 力。

4 日前-实时EV 调度模型

基于附录A 图A6 所示的调度框架，针对配电网和EV 进行多目标协同优化调度。本文综合考虑EV 里程需求、用户成本和电网安全等因素，以充分发挥EV 充放电潜力为导向，实现负荷需求的削峰填谷，增强电力系统稳定性。

4.1 日前-实时调度模型架构

4.1.1 目标函数

1）日前阶段

本文假设在日前阶段不发生出行链重构事件，以负荷需求波动最小和用户总成本最低为目标，对EV 进行充放电调度，构建日前阶段的多目标函数为:

式中:F为日前阶段的日负荷方差，用来表示配电网系统的负荷波动情况，F值越大表明负荷波动越明显，F值越小表明负荷变化越平稳；Pav为日平均负荷；F为日前阶段用户充放电总成本；和分别为t时段的充电电价和放电收益；θ为电池损耗费用；ΔTc为充电时长；ΔTd为放电时长。

2）实时阶段

由于充放电功率影响的无前溯性［32］，在实时阶段，只对出行链重构事件发生时段Et及之后的时段进行充放电调度优化。目标函数为:

式中:F为实时阶段的日负荷方差；F为实时阶段用户充放电总成本。

3）多目标函数处理

将日前阶段和实时阶段的日负荷方差和用户总充放电成本加权求和，得到两个阶段的评价函数:

式中:ω1、ω2、ω3和ω4为权重因子；FBD和FAD分别为日前阶段和实时阶段的评价函数。

4）极端状态下的评价函数:

式中:P为极端状态下t时段中可调度的EV 功率总 量；P为 第n辆EV 在t时 段 的 最 大 放 电 功 率；R为EV 在极端事件中的状态，值为1 表示消纳状态，值为2 表示供电状态。本文假设在极端状态下，EV 只保证一天最低的行程容量，仅考虑用户本身的里程焦虑值。

4.1.2 约束条件

1）EV 功率约束

EV 的充放电行为应在停驻阶段，同时EV 的充放电行为不能同时发生:

式中:上标min 和max 分别为最小和最大功率标识。

2）电池荷电状态约束

EV 电量受电池容量约束，因此，经过Δt时段之后，EV 电池的电荷状态约束为:

式中:Δtn，t为第n辆EV 在t时段的充放电时长。

3）EV 行程约束

EV 在充电结束后的电量能够满足之后的行程:

式 中:S为 第n辆EV 下 一 次 行 程 的 最 低 电 量，出 行链事件发生之后，该值需要进行立即调整；为 下一段充电的开始时段。式（50）描述了第n辆EV 的电量Sn，Tin，n经过Tin，n至Tout，n时段的充放电 过 程后，其电量应当满足行程约束并高于充电意愿值。

4）EV 充放电状态约束

EV 的运动状态和充放电状态不能同时发生，同时，EV 的充放电时间段不能超出该辆EV 的停驻时段，即

式中:T′out，n，t为出行链事件影响下的实际离网时间。

5）功率平衡

多态能源系统应当满足供需平衡:

6）充电意愿约束

用户的里程焦虑值应不大于用户的充电意愿:

式中:S为用户的里程焦虑阈值。

7）节点功率平衡

区域能源系统中整体电力负荷需求为该时段所有配电网充电负荷需求之和:

式中:Na为区域节点总数，a为节点编号；Pa，t表示配电网节点a在t时段的负荷需求。

4.2 模型求解

本文提出的日前-实时两阶段调度模型求解流程图如图2 所示。

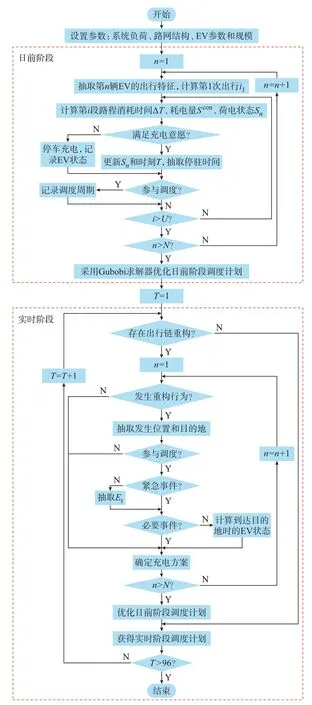
图2 模型的求解流程图Fig.2 Flow chart of model solution

5 案例分析

5.1 系统数据描述

以某城市区域的典型日负荷曲线为例进行仿真分析。采用峰时段、谷时段和平时段电价数据，具体数据详见附录A 表A3，共有45 条道路和26 个节点。

根据文献［33-34］，本文以在该区域内的50 辆EV 为例进行研究，EV 参数详见附录A 表A4。考虑到EV 负荷转移问题，将EV 的初始电量设置期望为8、方差为1 的正态分布。设置调度周期为24 h，以15 min 为时段间隔，划分为96 个时段，EV 接受充放电调度的周期为15 min。本文设置出行链重构事件发生的概率为100%，事件1、事件2 和事件3 发生的概率分别为25%、25%和50%。

5.2 不同场景的调度分析

本文研究5 种场景对调度结果的影响，结果如表1 所示。本文设基础负荷的日负荷方差为10 242.00。

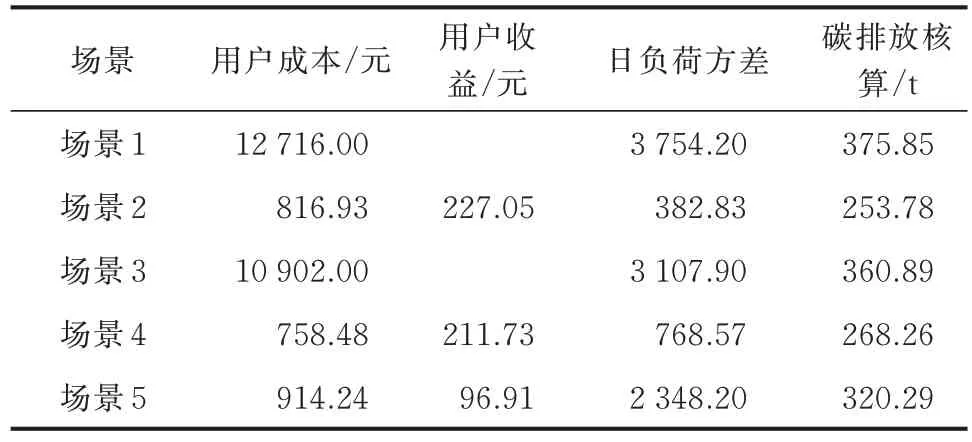
表1 不同场景下的调度结果Table 1 Dispatch results in different scenarios

场景1:所有EV 均不参与调度且不发生出行链重构事件。

场景2:所有EV 均参与调度但不发生出行链重构事件。

场景3:所有EV 均不参与调度但发生出行链重构事件。

场景4:所有EV 均参与调度且发生出行链重构事件。

场景5:EV 调度参与率为50%，且所有EV 均发生出行链重构事件。

图3 描述了不同场景下，EV 充放电对负荷需求的影响。通过5 个场景之间的对比可以看出，当EV参与充放电调度时，日负荷方差均会降低，总充放电成本也会减少。因此，EV 与电网稳定有效的互动有利于电网和用户双赢。

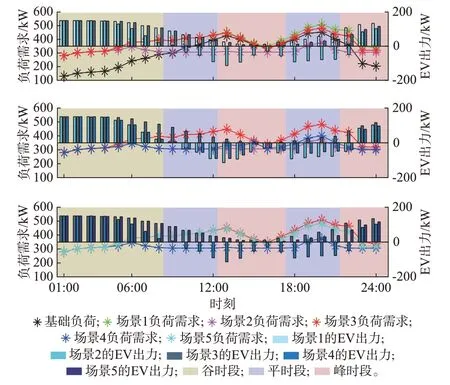
图3 不同场景下的总负荷和EV 出力Fig.3 Total load and EV output in different scenarios

场景3 的日负荷方差比场景1 的日负荷方差小646.36，充放电总成本降低1 814 元。这是因为当用户不参与调度时，直接影响日负荷方差和充电成本的因素是EV 接入电网的时间。因此，出行链重构事件发生后，用户接入电网的总时长减少，充放电总成本和日负荷方差降低。而且，当所有EV 均不参与调度时，由于出行链重构事件造成充电EV 数量下降，导致了负荷总需求的下降，引起了碳排放总量下降了15.04 t。

场景2 比场景1 日负荷方差减少了3 371.4，充放电总成本少12 126.12 元，场景4 比场景3 的日负荷方差降低了2 339.33，充放电总成本降低了10 355.25 元，比场景2 的日负荷方差增加了385.744，充放电总成本增加了43.13 元。对比结果表明，当用户参与调度时有利于电力系统的稳定和取得更低的成本。同时，EV 出行链重构事件会对既定调度计划产生破坏，增加负荷需求波动，不利于电力系统的稳定运行。随着负荷需求的增加，场景4 比场景2 的碳排放总量增加14.48 t。

场景4 出行链重构前后EV 的功率和负荷需求变化见附录B 图B1 和图B2。场景5 的日负荷方差相比较于场景3 的日负荷方差减少了759.641 4，场景4 的日负荷方差相比较于场景5 的日负荷方差减少了1 579.7。场景5 的充放电总成本相比较于场景3 减少了10 084.67 元，场景4 的充放电总成本相比较于场景5 减少了270.58 元，碳排放总量依次减少40.6 t、52.03 t。这说明EV 积极参与电力调度有利于提升电力系统稳定性和安全性，减少用户成本和碳排放。

5.3 事件类型敏感度分析

不同的事件类型对充放电计划的影响不同。事件1 的紧急性和重要性，会造成当前时段EV 立即离网或EV 以最大功率充电的行为。事件2 会在Et时段发生最大功率充电，并影响之后的调度计划。事件3 仅需调整Et之后时段的调度安排。本文设计了敏感度系数，如式（57）所示，体现不同事件在场景3、场景4 和场景5 中对充放电调度的影响，结果如表2 所示。

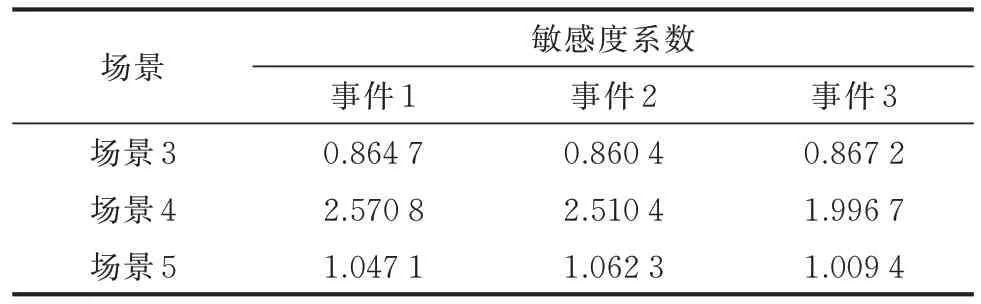
表2 各场景对不同事件的敏感度系数Table 2 Sensitivity coefficients of each scenario for different events

表2 计算了各场景对不同事件的敏感度系数的平均值，部分数据详见附录B 表B1。对比可见，用户参与度越低，3 种事件影响越小。当EV 不参与调度时，由于出行链重构会破坏之前的充电行为，产生了削峰现象，故敏感度系数小于1。当用户参与度超过50%时，对日前调度计划的重构导致敏感度系数大于1。

附录B 图B3 比较了同一辆EV 在3 种事件下的功率变化。通过对比图B3 和表2 可见，事件1 对调度计划的影响较大。这是因为事件1 导致EV 的充放电功率立即发生改变，而其余2 种事件均对之后时段进行调整，通过长时段的优化减少了事件造成的影响。

5.4 调度策略分析

5.4.1 调度目标分析

当充放电调度主体不同时，EV 的充放电调度策略也不尽相同，造成的影响也有差异。由表3 可见，不同的调度策略会导致不同的调度结果。

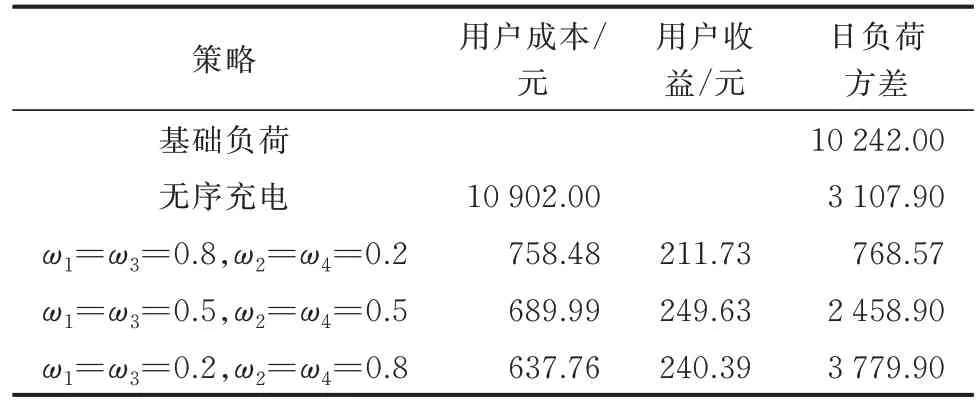
表3 不同调度策略EV 成本、收益和日负荷方差Table 3 EV costs, benefits, and daily load square deviation under different dispatch strategies

随着优化调度主体从电网逐渐转化到用户的过程中，日负荷方差依次增加1 690.33 和1 321，用户总成本依次下降106.39 元和42.99 元。从表3 可以看出，当以用户成本为优化主体时，相比于无序充电，用户总成本下降了10 504.63 元，但是日负荷方差相比于无序充电，增加了672。而以电网为优化调度主体时，相比于无序充电，日负荷方差下降了2 339.33。

5.4.2 调度规模分析

EV 集群的规模大小决定了单位时间内的调度潜力。因此，不同规模的EV 集群会有不同的调度结果，具体结果如表4 和图4 所示。

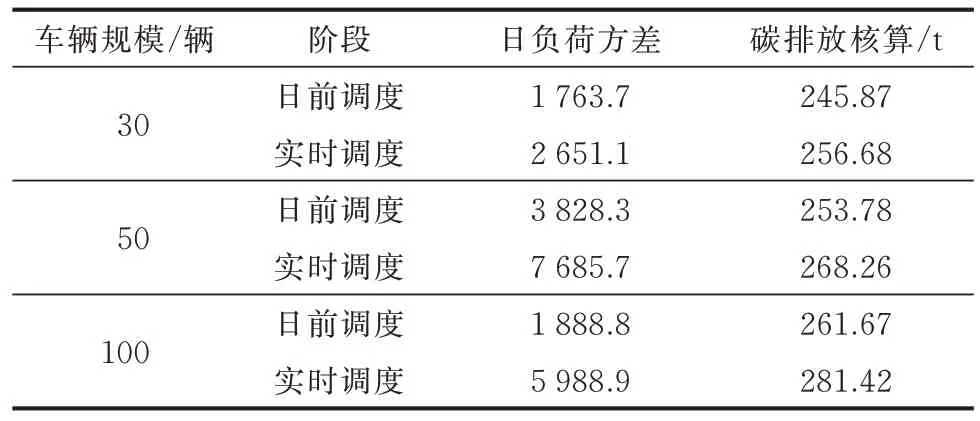
表4 不同车辆规模优化调度结果Table 4 Optimal dispatch results for different vehicle numbers

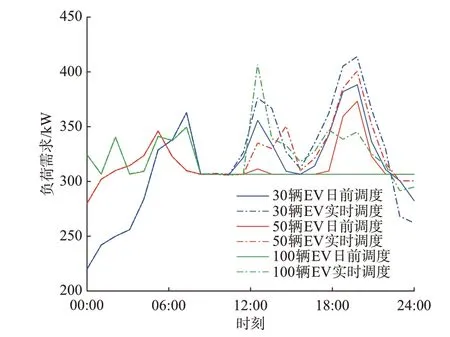
图4 不同车辆规模的负荷需求Fig.4 Load demand of different vehicle numbers

从表4 可以看出，随着EV 规模的逐渐上升，日前阶段的日负荷方差依次减少了1 380.87 和193.95，碳排放依次增加了7.91 t 和7.89 t；实时阶段的日负荷方差依次减少了1 882.53 和169.68，碳排放依次增加了11.58 t 和13.16 t。因此，EV 集群规模的扩大有利于负荷需求的稳定，但是负荷需求和碳排放总量也会随之增加。

同时，从表4 和图4 可以看出，随着车辆规模的上升，出行链重构事件也会增大对既定调度计划的破坏，增大负荷需求的波动。

5.4.3 用户参与度分析

本文提出EV 参与负荷需求总量λt来衡量EV与电网之间的能量互动，如式（58）所示。

由表5 和图3 的结果可见，随着EV 参与度的不断上升，EV 参与负荷需求总量也在上升，负荷需求曲线受优化调度影响，日负荷方差逐渐降低，负荷需求总量降低，碳排放总量随之减少。

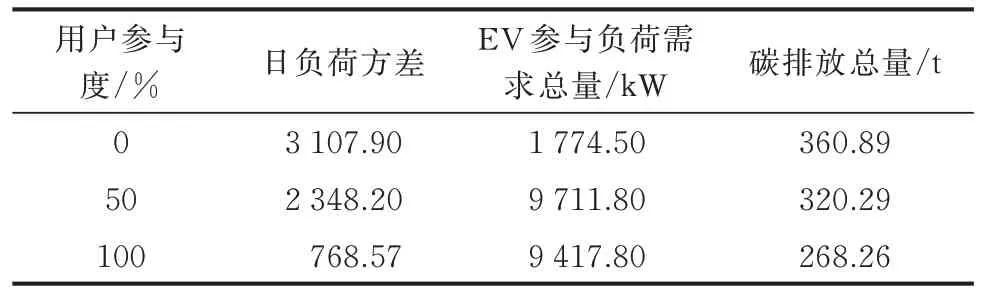
表5 不同用户参与度分析Table 5 Analysis of different user engagement levels

5.5 极端条件下EV 参与调度分析

5.5.1 主要供电机组瘫痪

在供电机组瘫痪的状态下，需要迅速且持久地向一级负荷和二级负荷供电。因此，分析3 种场景在各个时段的供电时长和平均负荷下的供电时长，结果如图5 和表6 所示。

表6 供电机组瘫痪时的平均供电时长Table 6 Average power supply duration when power supply unit is paralyzed

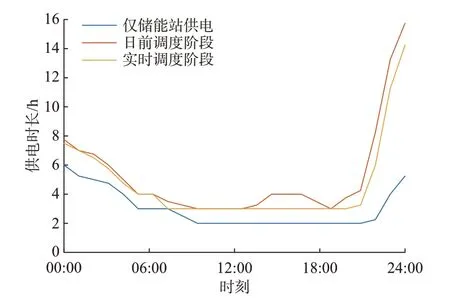
图5 各时段中备用能源的最长供电时长Fig.5 Longest power supply duration of backup energy in each time period

本文仅讨论了储能站储能处于下限临界值的供电时长。由图5 和表6 对比可以看出，在有EV 参与出力的场景下，供电时长有所增加，储能站协同EV在日前调度阶段和实时调度阶段的供电场景，相比较于仅储能站参与供电的场景，供电时长分别增加了135 min 和103 min。

由于EV 出行链的重构事件减少了EV 参与能量互动的时间，EV 在不发生重构事件的供电时长整体高于EV 发生重构事件时的供电时长。从图5可以看出，21:00 之后EV 参与供电的供电时长远高于仅储能供电的供电时长。这是由于21:00 之后，大量EV 返回居民区结束出行，增加了调度资源。

5.5.2 突发性供电增多

由于可再生能源具有突变性，本文仅讨论了储能站的储能处于上限临界值时，与EV 共同参与负荷消纳的情况。附录B 图B4 展示了各个时段可消纳负荷总量，表7 说明了平均消纳负荷总量。

表7 平均负荷消纳量Table 7 Average load consumption

对比储能站协同EV 在日前调度阶段和实时调度阶段的消纳场景可见，相比于仅储能站参与供电的场景，平均负荷消纳总量增加了117.84 kW·h 和101.09 kW·h。这一结果说明了EV 作为分布式储能资源，能够增加需求侧的负荷消纳能力。

附录B 图B4 描述了由于出行链重构事件，导致可调度EV 总量的减少，造成EV 参与能量互动时长的减少，引起各个时段可消纳负荷总量的降低。

5.6 不同风电规模分析

本文仅讨论常态下风电机组的余电通过储能站存储或弃风方式消纳。由图6 可见，随着风电规模的增加，火电机组的参与度迅速下降，削减了碳排放总量。

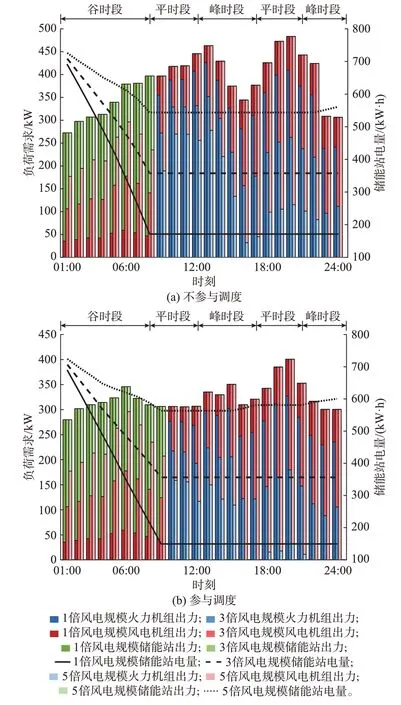
图6 不同风电规模储能站出力Fig.6 Output of energy storage stations with different wind power capacities

通过图6 中不同风电规模的储能站出力和表8中5 种场景在不同风电规模的碳排放核算对比可以看出，大量的EV 参与调度计划起到的削峰填谷和不参与调度造成的峰上加峰现象会改变总负荷需求，进而影响火电机组的出力和碳排放总量。同时，出行链重构事件对既定充放电计划的影响会由EV的调度参与度对火电机组出力产生不同的影响。

表8 不同规模风电场对比Table 8 Comparison of wind farms with different capacities

6 结语

为了解决多态场景下，EV 协同储能站在出行链重构事件中的电力调度问题，本文基于路网和配电网耦合场景，提出了EV 的出行链重构模型，并针对不同出行链重构事件，提供常态下EV 的充放电调度计划，以及极端条件下储能站协同EV 的调度策略。

实验结果表明，常态下的出行链重构事件会影响EV 的充放电过程，改变每个时段的负荷需求总量。同时，需求侧的影响也会波及供电侧可再生能源的利用率，影响碳排放总量。极端状态下的出行链重构事件会通过用户实际使用需求的改变，影响各时段的能源供给量和负荷消纳量。本文提出的调度策略能够有效缓解常态下的出行链重构事件对既定调度计划的破坏，进而最大限度地平抑负荷需求波动，以及增加储能站和EV 在极端条件下的供电量和负荷消纳量。

在后续的研究中将进一步讨论交通路网和配电网耦合的场景下，大规模EV 集群的调度问题，完善EV 与配电网之间的能量互动，研究EV 在复杂路网中的出行链重构行为。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。