基于结构张量全变差的CT图像去噪算法

吴丽沙 黄静 邹英慧 冀东江

摘  要：在计算机断层成像过程中，为了降低辐射剂量，往往采用稀疏角度投影数据，滤波反投影重建算法（Filtered BackProjection，FBP）具有重建速度快的优点，但在稀疏角度情况下重建得到的图像中存在较严重的条状伪影。针对此问题，该文研究采用基于结构张量全变差（The Structure tensor Total Variation）CT图像后处理去噪算法，该文中简称该算法为FBP-STV算法。为了验证该算法的可靠性，该文用2类模型进行数据仿真实验，并与FBP算法、截断全变分2类算法进行比较，实验结果表明，该文研究的FBP-STV算法，去噪效果相对较好，图像质量相对较高。

关键词：结构张量全变差；FBP滤波反投影算法；STV算法；FBP-STV算法；截断全变分

中图分类号：TP312      文献标志码：A          文章编号：2095-2945（2024）14-0005-04

Abstract： In the process of computed tomography， sparse angle projection data is often used to reduce radiation dose. Filtered back projection （FBP） reconstruction algorithm has the advantage of fast reconstruction speed， but there are serious strip artifacts in the reconstructed images in the case of sparse angles. In order to solve this problem， this paper studies the denoising algorithm of CT image post-processing based on structure tensor total variation. In this paper， the algorithm is called FBP-STV algorithm for short. In order to verify the reliability of the algorithm， data simulation experiments are carried out with two kinds of models and compared with FBP algorithm and truncated total variational algorithm. The experimental results show that the FBP-STV algorithm studied in this paper has a relatively good denoising effect and relatively high quality of images.

Keywords： total variation of structure tensor; filtered back projection（FBP） algorithm; STV algorithm; FBP-STV algorithm; truncated total variation

圖像重建算法中解析重建算法和迭代重建算法是2种最常用的图像重建算法。滤波反投影重建算法（Filtered BackProjection，FBP）[1]属于解析重建算法。为了降低重建图像的剂量，实际中可以采用稀疏角投影重建图像，但对于采用FBP重建算法，重建图像中有明显的条状伪影。为了解决这个问题，学者们研究了一系列的图像去噪算法。去噪算法包括有基于偏微分方程和变换域图像去噪[2]、基于改进阈值函数的TOFD小波去噪[3]、总变差（TV）等[4]。TV是一个凸泛函，其通常用于灰度图像，但也已扩展应用于向量值图像，其成功的主要原因是其能够重建具有清晰、边缘保持良好的图像。然而，其也有缺点，如过度平滑均匀区域和产生阶梯状伪影。

为了克服TV的局限性，文献中又提出了几种正则化泛函。其中包括适应图像变化惩罚的扩展，通过局部改变正则化权重[5]或通过结合图像的局部结构引入各向异性[6]。然而，这些方法从输入图像中提取局部信息，要么作为预处理步骤，要么作为优化问题的额外未知函数，而不是直接依赖于潜在图像。相反，所谓的各向异性TV（ATV）[7]通过引入一个依赖于未知图像本身的结构张量的“扩散”张量，来适应图像变化的惩罚。另一种旨在消除TV的阶梯效应的正则化方法涉及可以编码更高阶信息的泛函。这些正则化器促进分段线性而非分段常数的重建，并且与TV结合使用，如总广义变差（TGV）[8]和Hessian Schatten-范数正则化[9]。2015年结构张量全变差（The Structure tensor Total Variation，STV）[10]正则项被提出，该正则项应用在各种图像的反问题中。本文针对FBP算法在稀疏投影数据情况下重建图像中存在条状伪影这一问题，将STV引入到FBP重建算法当中，简称为FBP-STV算法。FBP-STV被用来约束重建图像中每个点的结构张量的特征值。

本研究在得到结构张量TV模型的情况下将其与原图、截断TV[11]及FBP算法处理后的图像进行图像去噪对比分析。采用峰值信噪比（PSNR）和均方误差（MSE）[12]等指标来评估重建图像的质量。

1  图片去噪算法

1.1  FBP滤波反投影算法

滤波反投影是指对投影数据先进行滤波，然后再进行反投影算法。其中u（x，y）为反投影后的图像，该算法如公式（1）所示

式中：|ω|是一维滤波器函数，而[ ]中所包括的为一维傅里叶反变换，ρ=xcosθ+ysinθ是一条直线的法线表示，且ρ对于ω来说是一个常数，G（ω，θ）是投影的一维傅里叶变换，如公式（2）所示

得到，在公式（2）中ω是频率变化量，g（ρ，θ）是固定的θ值下得到的对ρ的完整投影。

1.2STV结构张量算法[8]

在该算法中STV被用来约束图像中每个点的结构张量的特征值，与传统TV的算法相比，基于STV的算法在图像恢复方面具有较大优势。结构张量主要用于区分图像的平坦区域、边缘区域与角点区域。在数学上，STV可以表示如下

3  实验与分析

本文选取2幅图像进行试验，在0～179°范围内等间隔采样了90个投影，分别采用FBP算法、FBP-STV算法、截断TV算法来进行实验，并通过主客观两方面进行评价。

3.1  第一幅图实验结果分析

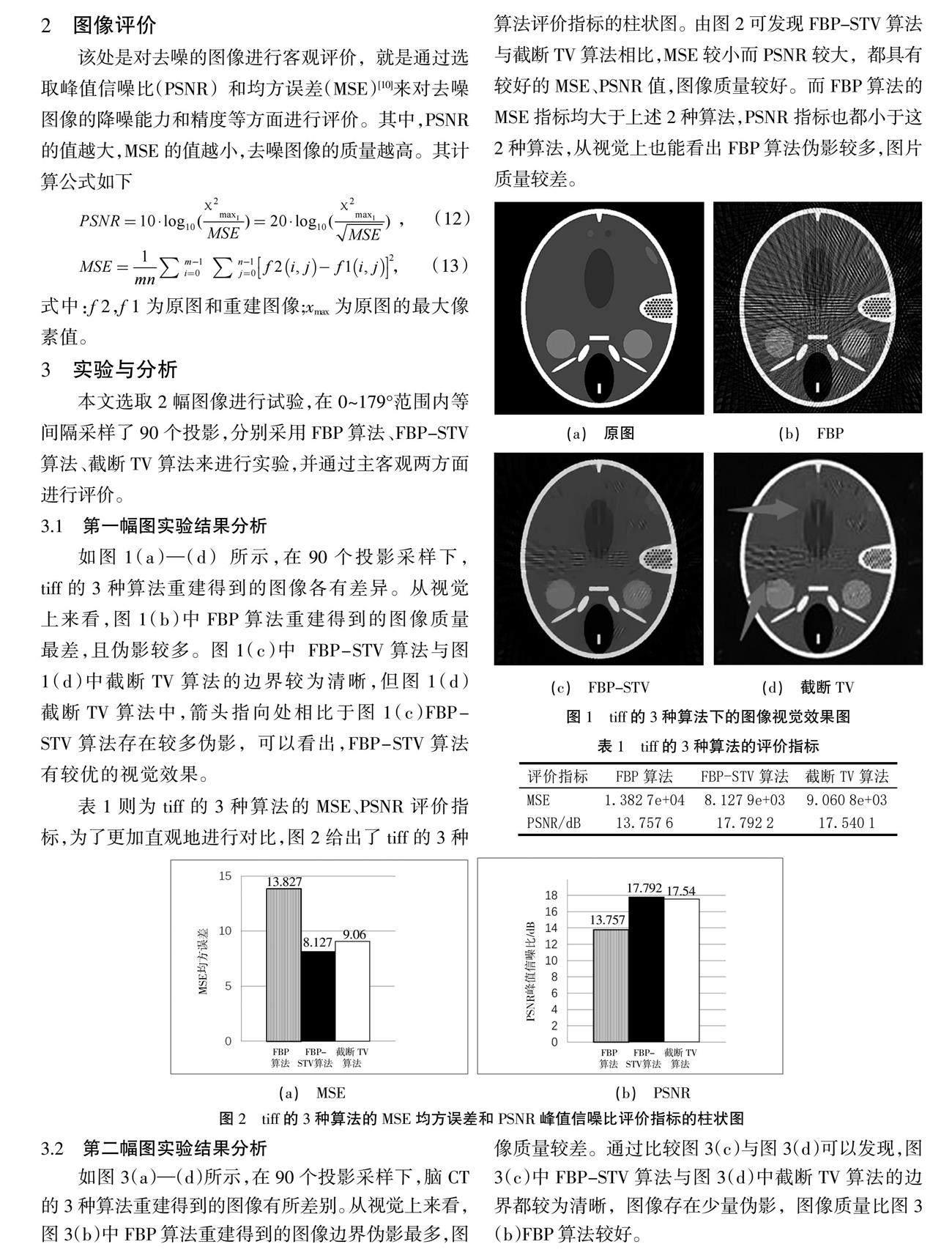
如图1（a）—（d） 所示，在90个投影采样下，tiff的3种算法重建得到的图像各有差异。从视觉上来看，图1（b）中FBP算法重建得到的图像质量最差，且伪影较多。图1（c）中 FBP-STV算法与图1（d）中截断TV算法的边界较为清晰，但图1（d）截断TV算法中，箭头指向处相比于图1（c）FBP-STV算法存在较多伪影，可以看出，FBP-STV算法有较优的视觉效果。

表1则为tiff的3种算法的MSE、PSNR评价指标，为了更加直观地进行对比，图2给出了tiff的3种算法评价指标的柱状图。由图2可发现FBP-STV算法与截断TV算法相比，MSE较小而PSNR较大，都具有较好的MSE、PSNR值，图像质量较好。而FBP算法的MSE指标均大于上述2种算法，PSNR指标也都小于这2种算法，从视觉上也能看出FBP算法伪影较多，图片质量较差。

3.2  第二幅图实验结果分析

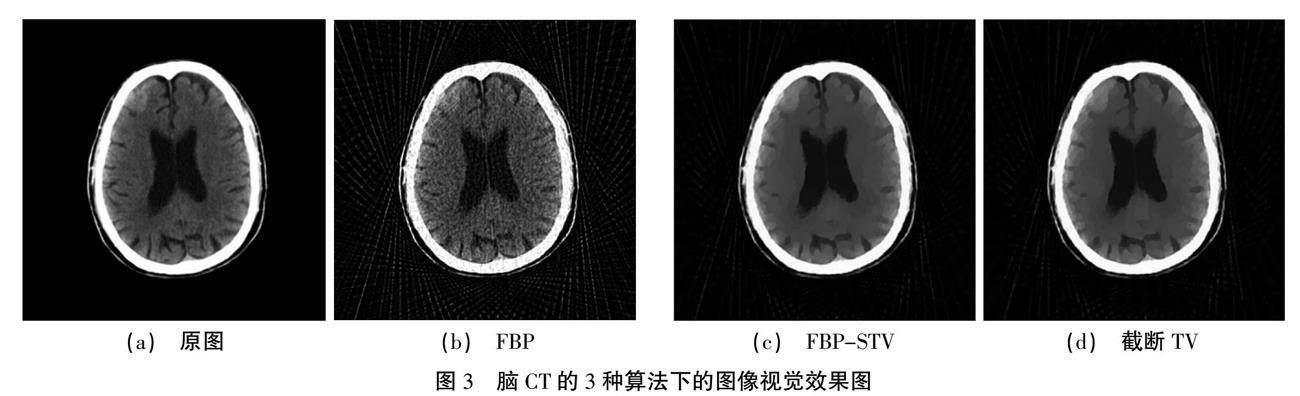
如图3（a）—（d）所示，在90个投影采样下，脑CT的3种算法重建得到的图像有所差别。从视觉上来看，图3（b）中FBP算法重建得到的图像边界伪影最多，图像质量较差。通过比较图3（c）与图3（d）可以发现，图3（c）中FBP-STV算法与图3（d）中截断TV算法的边界都较为清晰，图像存在少量伪影，图像质量比图3（b）FBP算法较好。

表2则为脑CT的3种算法的MSE、PSNR评价指标。为了更加直观地进行对比，图4给出了脑CT的3种算法评价指标的柱状图。由图4可发现FBP-STV算法较其他2种算法评价指标都要好一些，客观评价表明该算法优于其他2种算法。

4  结论

本文在稀疏角度采用投影数据情况下，首先采用FBP重建出初始图像，然后采用了STV对重建图像进行约束，为了证明所研究算法的有效性，将该算法与其他2种算法（FBP和截断TV）进行了去噪对比实验，比较实验结果表明，FBP-STV算法与其他2种算法相比，在去除条状伪影同时可以对边界的结构有很好的保护效果。

参考文献：

[1] Rafacl C. Gonzalez，Richard E. Woods.数字图像处理[M].4版.阮秋琦，阮宇智，译．北京：电子工业出版社，２０２０：２５６－２７2.

[2] 张敏.基于偏微分方程和波域自适应图像去噪方法研究[D].南京：南京信息工程大学，2020.

[3] 薛峰.基于改进阈值函数的TOFD图像小波去噪[J].无损检测，2０２３，４５（８）：６２－66.

[4] RUDIN L Ｉ，ＯＳＨER Ｓ， ＦＡＴEMI E. Nonlinear total variation based noise removal algorithms[J].Physica D Nonlinear Phenomeｎａ，１９９２，６０（１－４）：２５９－２６８．

[5] DONG Y，ＭＩＣＨＡＥＬ Ｈ． Ｍｕｌｔｉ－ｓｃａｌｅ ｔｏｔａｌ ｖａｒｉａｔｉｏｎ ｗｉｔｈ ａｕｔｏｍａｔｅｄ ｒｅｇｕｌａｒｉｚａｔｉｏｎ ｐａｒａｍｅｔｅｒ ｓｅｌｅｃｔｉｏｎ ｆｏｒ ｃｏｌｏｒ ｉｍａｇｅ ｒｅｓｔｏｒａｔｉｏｎ[C]//Inｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｓｃａｌｅ Ｓｐａｃｅ ＆ Ｖａｒｉａｔｉｏｎａｌ Ｍｅｔｈｏｄｓ ｉｎ Ｃｏｍｐｕｔｅｒ Ｖｉｓｉｏｎ．Ｓｐｒｉｎｇｅｒ－Ｖｅｒｌａｇ，２００９．

[6] ＳＥＴＺＥＲ Ｓ， ＳＴＥＩＤＬ Ｇ， ＴＥＵＢＥＲ Ｔ． Ｒｅｓｔｏｒａｔｉｏｎ ｏｆ ｉｍａｇｅｓ ｗｉｔｈ ｒｏｔａｔｅｄ ｓｈａｐｅs[J].Nｕｍｅｒｉｃａｌ Ａｌｇｏｒｉｔｈｍｓ，２００８，４８（１－３）：４９－６６．

[7] ＧＲＡＳＭＡＩＲ Ｍ， ＬＥＮＺＥＮ Ｆ． Ａｎｉｓｏｔｒｏｐｉｃ ｔｏｔａｌ ｖａｒｉａｔｉｏｎ ｆｉｌｔｅｒｉｎｇ[J].Aｐｐｌｉｅｄ ｍａｔｈｅｍａｔｉｃｓ ａｎｄ ｏｐｔｉｍｉｚａｔｉｏｎ，２０１０（３）：３２３－３３９．

[8] ＢＲＥＤＩＥＳ Ｋ， ＫＵＮＩＳＣＨ Ｋ， ＰＯＣＫ Ｔ． Ｔｏｔａｌ ｇｅｎｅｒａｌｉｚｅｄ ｖａｒｉａｔｉｏn[J].SIＡＭ Ｊｏｕｒｎａｌ ｏｎ Ｉｍａｇｉｎｇ Ｓｃｉｅｎｃｅｓ，２０１０，３（３）：４９２－５２６．

[9] ＬＥＦＫＩＭＭＩＡＴＩＳ Ｓ， ＷＡＲＤ Ｊ Ｐ， ＵＮＳＥＲ Ｍ． Ｈｅｓｓｉａｎ sｃｈａｔｔｅｎ－ｎｏｒｍ ｒｅｇｕｌａｒｉｚａｔｉｏｎ ｆｏｒ ｌｉｎｅａｒ ｉｎｖｅｒｓｅ ｐｒｏｂｌｅｍs[J].ＩＥＥＥ Ｔｒａｎｓ Ｉｍａｇｅ Ｐｒｏｃｅｓｓ，２０１３，２２（５）：１８７３－１８８８．

[10] ＬＥＦＫＩＭＭＩＡＴＩＳ Ｓ， ＲＯＵＳＳＯＳ Ａ， ＭＡＲＡＧＯＳ Ｐ， ｅｔ ａｌ． Ｓｔｒｕｃｔｕｒｅ ｔｅｎｓｏｒ ｔｏｔａｌ ｖａｒｉation[J]. ＳＩＡＭ Ｊｏｕｒｎａｌ ｏｎ Ｉｍａｇｉｎｇ Ｓｃｉｅｎｃｅｓ， ２０１５，８（２）： １０９０－１１２２．

[11] ＤＯＵ Ｚ， ＳＯＮＧ Ｍ， ＧＡＯ Ｋ， ｅｔ ａｌ． Ｉｍａｇｅ ｓｍｏｏｔｈｉｎｇ ｖｉａ ｔｒｕｎｃａｔｅｄ ｔｏｔａｌ ｖａｒｉａｔｉｏｎ[J].ＩＥＥＥ Ａｃｃｅｓｓ，２０１７，５：２７３３７－２７３４４．

[12] 黃小乔，石俊生，杨健，等．基于色差的均方误差与峰值信噪比评价彩色图像质量研究[D].昆明：云南师范大学，２００７．