基于I-GWO-BP模型的临近建筑沉降预测

周 渊 （江西理工大学 土木与测绘工程学院，江西 赣州 341000）

0 引言

基坑开挖施工会对周围土体造成扰动，破坏地层的完整性，处理不慎可能会引起地面沉降塌陷以及临近建筑物的不均匀沉降，甚至倾斜破坏，对市民的正常生活造成严重的不良影响，甚至造成巨大的经济损失和人员伤亡。基坑工程的建设并不是仅仅指基坑本身的稳定与安全，如何有效控制基坑开挖引起的地表不均匀沉降并保护好临近建筑的安全，是目前城市地下工程亟待解决的一项重要难题[1]。在基坑工程施工期间，对基坑周边建筑物进行监测，是保证安全施工的重要手段。王怡慎等[2]结合苏州某基坑工程，建立BP神经网络模型对临近建筑沉降进行多步预测，结果表明该模型预测精度较高，平均误差均小于5.5%，与实测值吻合较好。安月等[3]结合某明挖地铁站基坑工程，基于NAR 神经网络对基坑周围地表和临近建筑位移监测数据进行多步预测分析，并将临近建筑历时位移预测法与BP、LSTM 两种模型比较，结果表明NAR 神经网络预测在预测临近建筑位移预测上具有更佳的拟合和泛化能力。

BP 神经网络模型在岩土基坑邻域应用最成熟，许多专家也提出了其他算法优化BP 神经网络模型，来改善BP 神经网络模型局部易出现的极值问题。本文主要通过4 个引起临近建筑沉降的主要影响因素，基于I-GWO-BP 神经网络模型，预测基坑开挖引起临近浅基础建筑的沉降值，以便对临近浅基础建筑沉降做出预警和评价。

1 I-GWO-BP神经网络的建立

1.1 BP神经网络

BP 神经网络是一种多层前向反馈型的网络模型，是前向网络的核心，因多层前向神经网络的权值调整采用的是反向传播学习的算法(Back Propagation)而称为BP神经网络。以三层前馈网（单隐层前馈网）为例来介绍BP神经网络学习算法。所谓三层包括了输入层、隐层和输出层，如图1所示。通过输入向量X对样本数据进行训练，计算输出值与期望值的误差，采用反向传播不断调整权值降低输出误差。但BP 神经网络收敛速度较慢并且容易陷入局部最小和过拟合等缺陷。

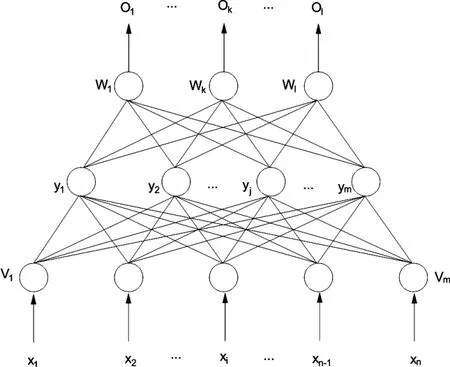
图1 三层BP神经网络

1.2 改进灰狼算法

灰狼优化算法是一种基于种群的群体智能算法，灵感来自自然界中灰狼的社会领导和狩猎行为。在种群中主要分为4 类狼，处于第一级的alpha（α）狼，为狼群的领导者；处于第二级的beta（β）狼；处于第三级的delta（δ）狼和处于最底层的omega（ω）狼。在GWO算法中，狩猎（优化）是由alpha、beta 和delta 指导的，omega 狼听从这三类狼，并在上级的指挥下有序对猎物进行狩猎，如图2 所示。由于其简单、采用的控制参数较少且易于实现，GWO 已被广泛用于求解不同的优化问题。GWO 虽然简单易学，但寻优过程中优于初始种群的随机性容易陷入局部最优。

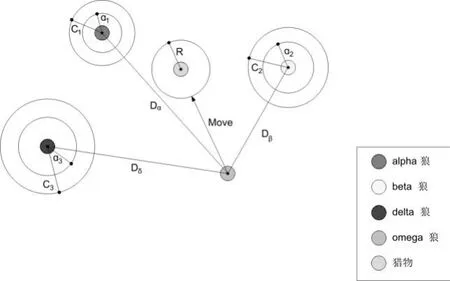
图2 GWO中的位置更新

为了优化初始种群，使收敛因子a随着迭代次数从2到0呈非线性递减，在初期递减程度减缓，能够更好地寻找全局最优解，到了后期递减程度增强，能够更加精确地寻找局部最优解，如此便能更有效地平衡算法的全局搜索和局部搜索能力。张童康等[4]提出一种新的非线性收敛因子计算方式：

式中，a为收敛因子；t 为当前迭代；max为最大迭代次数。

为了合理分配位置权重，避免算法陷入局部最优，郭振洲等[5]引入一种基于指导位置向量模值的比例权重，通过调节权重，在不断动态平衡调节算法的全局和局部搜索能力的同时加快算法的收敛，即引入权重比例计算：

式中，ω1表示omega 狼对alpha 狼的学习率；ω2表示omega 狼对beta 狼的学习率；ω3表示omega 狼对delta 狼的学习率。

1.3 建立I-GWO-BP神经网络沉降预测模型

改进灰狼算法优化BP 神经网络的主要思想是通过改进灰狼算法对BP 神经网络的权值和阈值进行寻优，再把最优权值和阈值赋给BP 神经网络来完成预测[6]。通过灰色关联度对临近浅基础建筑沉降的影响因素定量分析，以及利用有限元对主要影响因素进行敏感性分析，得出基坑开挖深度、临近建筑的层数、土体重度γ 和土体内摩擦角φ是引起临近建筑物沉降的4 个主要因素。通过I-GWO 对BP 神经网络的55 个权值和阈值进行寻优，并将最优初始权值和阈值赋予BP神经网络进行沉降值预测，用训练好的模型进行仿真，将实测值与改进前后的GWO-BP 神经网络预测值及BP神经网络预测值进行对比。

I-GWO-BP 神经网络的具体步骤如下。

①确定BP 神经网络结构为3 层4-9-1 网络（输入层为4 个神经元、隐含层为9 个神经元、输出层为1 个神经元）。可得到所需优化的输入层到隐含层的权值为36 个，隐含层到输出层的权值为9个，阈值为10 个。最大迭代次数为10，最大训练次数为100，学习速率为0.01，训练目标最小误差为0.001。

②灰狼种群初始化。灰狼种群数量为30，初始位置的上界和下界分别取-1和1。

③确定神经网络的传递函数为logsig 型函数、训练函数为traninlm 型函数和适应度函数为预测输出值和实测值的均方误差。

④将4 个主要影响因素作为输入层输入，计算适应度值更新所有灰狼的位置以及参数。

⑤得出误差及所对应alpha的位置。

⑥判断是否满足设定误差或者达到最大迭代次数。若不满足，则重复步骤④～⑥，直至满足条件。

⑦得出最优权值和阈值及领头狼alpha的位置和沉降预测值。

2 数据的选取与处理

样本数共52 项，为了防止出现“过拟合”，将样本分成4份，前3份作为训练样本进行训练学习，最后1 份作为预测样本进行测试学习。训练样本的作用是训练整个神经网络模型，测试样本的作用是测试预测模型的泛化能力[4]，具体数据如表1所示。

表1 学习和测试样本

3 预测对比分析

图3 GWO-BP适应度曲线

图4 I-GWO-BP适应度曲线

3.1 改进前后的GWO-BP神经网络预测适应度对比分析

在初始迭代时，I-GWO-BP 适应度低于GWO-BP 适应度，且GWO-BP 到第9 次达到最小适应度，而I-GWO-BP在第二次迭代时就已经达到最小适应度，这表明I-GWO-BP精度更高。

3.2 改进前后的GWO-BP神经网络预测与BP神经网络预测结果对比

由图5、图6 可知，改进前后的GWO-BP 预测结果均优于BP 预测，且I-GWO-BP 预测精度更高，预测结果也与实测结果更吻合。

图5 GWO-BP与BP预测结果对比

图6 I-GWO-BP与BP预测结果对比

由表2 可知，I-GWO-BP 预测值相对于实测值普遍偏小，虽然在这三种模型中预测结果最佳，但1、3、8、9、12、13项数据预测值与实测值相比误差较大，原因为数据1 所给的实测数据为采取保护措施后建筑的沉降，数据3 的开挖土层中夹卵石土层，该土层的内摩擦角受条件所限基本取经验值，数据8和9周围环境较复杂，两侧均有其他建筑存在，数据12 和13 为结合实际工程的有限元模拟研究的沉降值，无实测数据支撑。

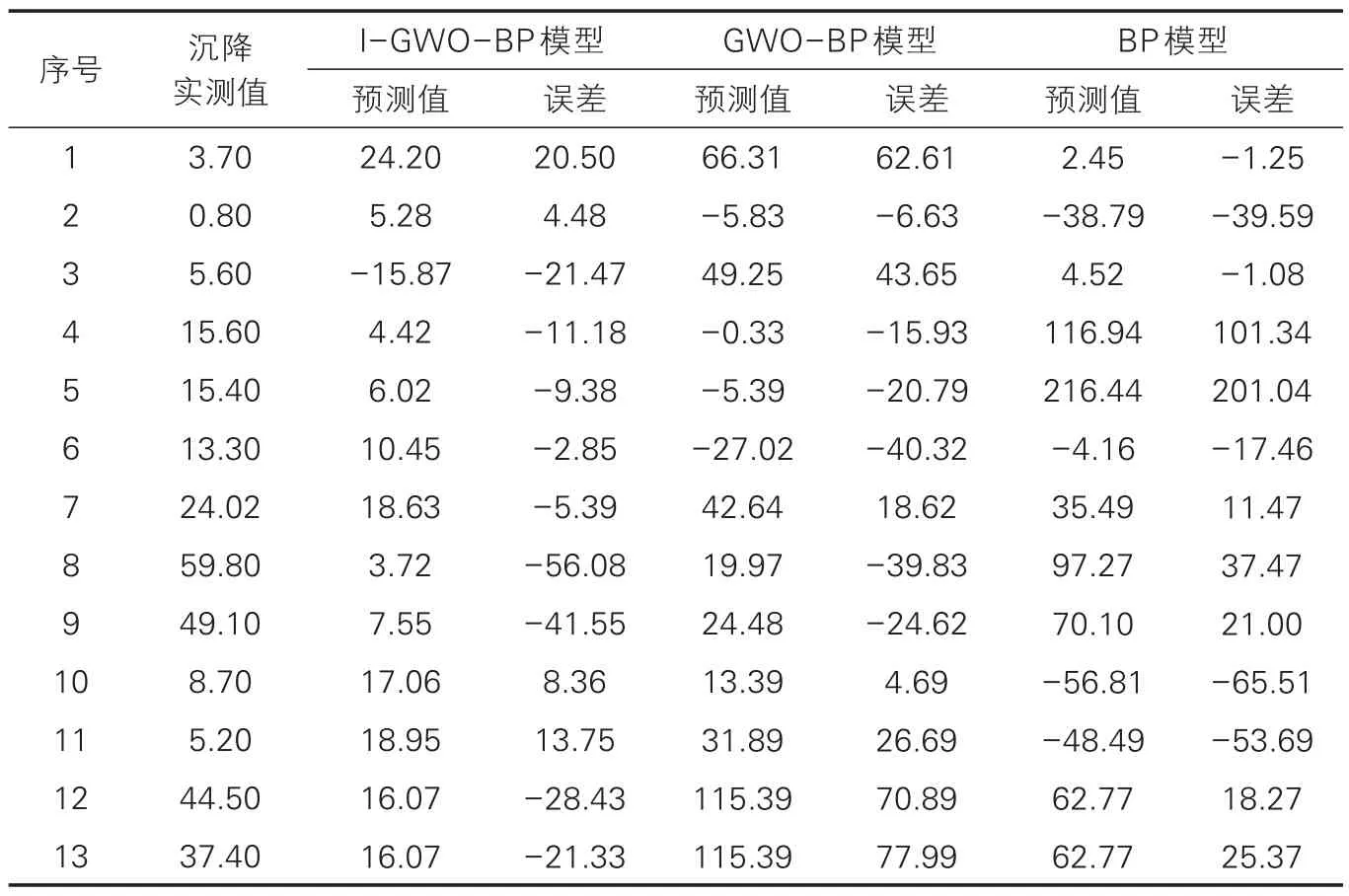
表2 测试组预测结果对比（单位：mm）

4 结论

在对实际工程进行临近建筑沉降预测中，在预测效果上I-GWO-BP>GWO-BP>BP神经网络模型，I-GWOBP 不管在收敛速度上还是在预测精度及误差上都表现最好。

本文提出的预测方法仅在已知基坑开挖深度、临近建筑的层数、土体重度γ和土体内摩擦角φ这4 项数据基础上，预测出临近建筑的大致沉降值，但由于只考虑了这4 个影响因素，模型还是有一定的误差存在，除个别复杂环境下的预测结果误差较大，最大误差为56mm，最小为20mm 左右，其余预测结果误差均控制在10mm 左右，故在实际过程中，该预测模型是合理可行的。