接触问题的三角形载荷离散FFT加速算法

陈楠 朱凯 蒋志桢 龚诗雨 李璞 金晓清

摘要：接觸问题控制方程的有效求解，往往涉及到复杂的数学理论知识，而在实际工程应用中，接触应力分布又具有高度随机性。为高效快速求解任意载荷分布下固体的接触响应，基于三角形载荷离散单元，嵌入离散卷积快速傅里叶变换（DC-FFT）算法，提供了一种高精度、高可靠度的计算方法。相比于通常采用的分段均布载荷离散方法，三角形单元的解析求解略显复杂，但能更好地模拟接触载荷任意分布的特性，对于接触边缘处载荷由零递增或递减为零的情况，也可以予以充分考虑。为优化三角形载荷离散单元的求解方法，根据接触影响系数矩阵的“激励-响应”特性，推导了三角形载荷单元和均布载荷单元作用下的应力分量解析解。通过构造包含影响系数矩阵的离散卷积形式应力解，将某一目标节点在所有载荷单元作用下，重复度极高的矩阵运算叠加过程，采用DC-FFT算法来简化加速计算。通过程序编程计算，分析验证了所提出算法的精确度和高效性。

关键词：三角形单元；接触应力；DC-FFT；数值解；应力场

中图分类号：TH123          文献标志码：A      文章编号：1000-582X（2024）02-095-11

FFT acceleration algorithm for contact problems based on triangular element discretization

CHEN Nan1a， ZHU Kai1a， JIANG Zhizhen1a， GONG Shiyu1a， LI Pu2， JIN Xiaoqing1a，1b

（1a. College of Aerospace Engineering; 1b. State Key Laboratory of Mechanical Transmissions， Chongqing University， Chongqing 400044， P. R. China; 2. School of Science， Harbin Institute of Technology， Shenzhen 518055， Guangdong， P. R. China）

Abstract： Effectively solving the governing equations for contact problems often involves complex mathematical theory， while the distribution of contact stress is highly random in practical engineering applications. This study proposes a novel algorithm based on the triangular load discrete element and the discrete convolution fast Fourier transform （DC-FFT） algorithm. This algorithm provides a high-precision and reliable method for efficiently solving the contact response of a solid under any load distribution. Compared to the commonly used uniform load element discrete method， the analytical solution of the triangular element is more complex. However， it better simulates the characteristics of contact load distribution， accounting for situations where the load at the contact edge increases from zero or decreases to zero. The stress component under the action of the triangular and uniform load elements is derived based on the “excitation-response” characteristics of the contact influence coefficient matrix. This information is used to optimize the solution method of the triangular load discrete element. By constructing the stress solution in the form of a discrete convolution， including the influence coefficient matrix， the stress superposition effect of a target node under the action of all elements can be further simplified and accelerated by using the DC-FFT algorithm for highly repetitive matrix calculations. Programming and calculation analysis show that the proposed algorithm based on the triangular load element is accurate and efficient.

Keywords： triangular element; contact stress; DC-FFT; numerical solution; stress field

随着机械装备在高速度、高频率和高精度等方面的需求越发苛刻，由局部压力波动和微观接触形貌所造成的影响变得越发不可忽视[1]，由此引起的表界面接触应力，进一步呈现出更加随机和任意的分布特征。对上述接触应力分布的高精度捕捉和分析，是揭示机械零部件失效和破坏的重要理论依据。然而，由于任意载荷分布情况下的封闭解析解很难获得，数值计算方法成为求解此类问题的一种有效而通用的手段。早期对这类问题的研究是通过应用已知函数的无穷级数代替表面接触压力分布来求解的[2]，但是这种方法必须选择正确的已知函数，否则会导致极大的误差，而大多数情况下这些函数却很难得到。Nowell等[3]利用三角形离散单元求解平面薄层弹性接触问题的方法，显示出了较高的计算精度，为任意分布载荷的接触问题分析提供了一种有效思路，然而该方法消耗的时间较长。

在数值求解接触问题时，由于在目标域边界处容易产生周期性误差，为了获得更准确的结果，常常要以计算效率为代价，选择远大于目标尺寸的计算域，来弥补计算结果的误差。基于快速傅里叶变换（fast Fourier transform，FFT）的接触问题分析方法能大大减小计算负担，是解决大规模复杂问题的有力工具。Ju等[4]首次将FFT引入到计算接触问题的线性卷积过程中，他们利用傅里叶变换将接触的时域问题转换为傅里叶空间下的频域问题，通过结合频谱分析和FFT，为粗糙表面接触的计算提供一种高效的技术。相关研究表明[5?6]，离散卷积快速傅里叶变换（discrete convolution fast Fourier transform，DC-FFT）算法在处理复杂的平面接触问题时更便捷、更有效。Wang等[7]总结了涉及快速傅里叶变换（FFT）的不同算法，对不同的接触问题、误差控制，以及不同几何形状、材料和物理问题的求解方案进行了分析。Li等[8]利用FFT研究了无黏着接触区内外的表面张力。基于FFT的数值方法也适用研究粗糙表面的微动接触问题[9]。快速傅里叶变换也可以通过和Westergaard基本解结合，来有效地解决约束最小化问题，严格验证接触正交性[10]。Yu等[11]将FFT与共轭梯度法相结合，用于研究三维热弹性滚动接触的稳态模型。在研究微动接触和微滑接触时[12]，共轭梯度法和FFT的结合显示出来更高的计算效率和准确性。在接触球轴承的研究中[13]，FFT可以被用来求解椭圆接触下，有油膜润滑的轴承内部接触载荷的分布。黏弹性问题的瞬态及稳态响应也可以通过FFT来提高计算效率[14]。

在复杂接触应力情况下，为达到计算精度和计算消耗时间的优化，笔者提出用重叠的三角形单元离散任意函数形式分布的表面接触应力，来求解受载固体内任意位置应力的方法。推导均布载荷单元和三角形载荷下的单元解，并进一步获得卷积形式的应力公式，通过借助DC-FFT方法，实现加速计算。通过考虑赫兹分布形式的接触应力，数值解与解析解显示出较好的吻合度，验证了所提出的数值计算方案的有效性。此外，通过控制单元宽度和单元数量，对比均布载荷单元离散与三角形单元离散计算出的应力场，通过对比分析2种离散方法的相对误差，表明所提出的基于三角形载荷单元的快速傅立叶计算方法的优越性。最后，给出单元直接叠加方法与本文算法的效率对比，分析不同单元数量对CPU时间的影响。

1 任意载荷作用下弹性半平面模型

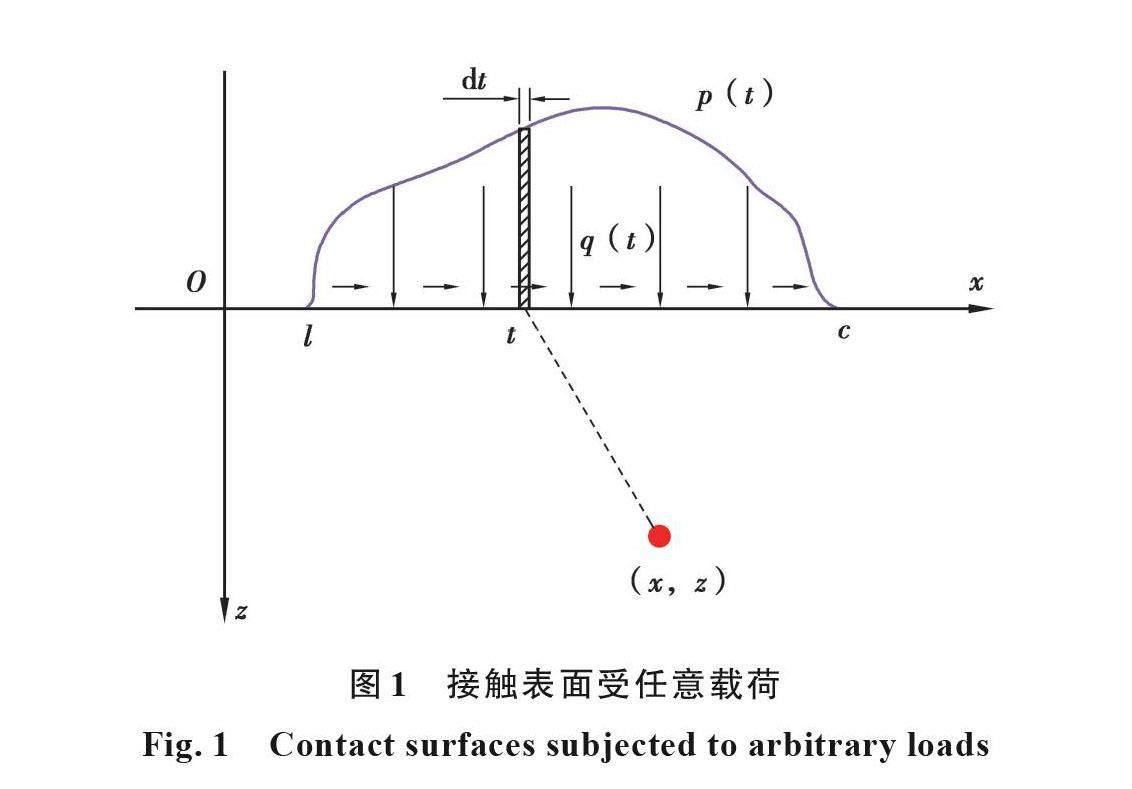
在弹性半平面接触问题中，由于接触问题的复杂性，可能会导致接触表面载荷分布的随意性，表面接触区域（l，c）上的任意载荷可分解为法向载荷p（t）及切向载荷q（t），如图1所示。

在表面距离O点t处取微元宽度dt，则点（x，z）处的应力分量可以表示为

{（σ_x=-2z/π ∫_l^c?〖（p（t）〖（x-t）〗^2）/（[〖（x-t）〗^2+z^2 ]^2 ） dt-〗  2/π ∫_l^c?〖（q（t）〖（x-t）〗^3）/（[〖（x-t）〗^2+z^2 ]^2 ） dt ，〗@σ_z=-（2z^3）/π ∫_l^c?〖（p（t））/（[〖（x-t）〗^2+z^2 ]^2 ） dt-〗  （2z^2）/π ∫_l^c?〖（q（t）（x-t））/（[〖（x-t）〗^2+z^2 ]^2 ） dt 〗，@τ_xz=-（2z^2）/π ∫_l^c?〖（p（t）（x-t））/（[〖（x-t）〗^2+z^2 ]^2 ） dt-〗  2z/π ∫_l^c?〖（q（t）〖（x-t）〗^2）/（[〖（x-t）〗^2+z^2 ]^2 ） dt 〗 。）┤  （1）

式（1）中包含奇异积分项。在载荷p（t），q（t）较复杂的情况下，各应力分量的解析求解较为困难，因此，通常采用数值方法进行离散求解。

2 数值方法

2.1 均布载荷单元的单元解

现行数值计算方法，通常采用分段均布载荷单元对载荷进行离散，当单元划分得足够精细时也可以较好地接近真实解。均布载荷单元载荷如图2所示，载荷分布区域半宽为b，常数p、q分别为法向和切向载荷的大小，r_1 、r_2 、r分别为表面上（b，0）（-b，0）、O到响应点（x，z）的距离。

将载荷p代入公式（1），推导得到法向均布載荷单元作用下响应点的各应力分量为

{（σ_x=-p/π [arctan （b-x）/z+arctan （b+x）/z ├ -（z（b+x））/（r_1^2 ）+（z（x-b））/（r_2^2 ）]  ，┤@σ_z=-p/π [arctan （b-x）/z+arctan （b+x）/z ├ +（z（b+x））/（r_1^2 ）-（z（x-b））/（r_2^2 ）]  ，┤@τ_xz=-（z^2 p）/π （1/（r_1^2 ）-1/（r_2^2 ））  。）┤    （2）

其中，

{（r_1^2=〖（b-x）〗^2+z^2  ，@r_2^2=〖（b+x）〗^2+z^2  ，@r^2=x^2+z^2  。）┤     （3）

同理，代入q，得到切向均布单元载荷作用下响应点的各应力分量为

{（σ_x=-q/π （z^2/（r_2^2 ）-z^2/（r_1^2 ）+2ln r_2/r_1 ）  ，@σ_z=-（z^2 q）/π （1/（r_1^2 ）-1/（r_2^2 ））  ，@τ_xz=-q/π [arctan （b-x）/z+arctan （b+x）/z ├ -（z（b+x））/（r_1^2 ）+（z（x-b））/（r_2^2 ）]  。┤ ）┤  （4）

利用均布单元离散任意载荷分布的接触问题时，由于相邻单元的载荷大小不尽相同，导致各个单元之间的连接是跳跃间断的。应用该方法求解位移时，会出现单元交接处的位移梯度无穷大，进而得到的结果也不够光滑连续，尤其是当接触载荷从零开始变化的时候，任意载荷大小的均布单元也无法捕捉到接触边界上载荷为零的情况。

2.2 三角形载荷的单元解

为克服上述均布载荷单元的不足，将受载面上任意法向和切向载荷用一系列重叠等宽的三角形单元进行离散。相应的单个三角形分布的载荷单元如图3所示。

由图3可知，三角形单元的法向和切向载荷在-a～a的范围内，从0线性增加至最大值，再线性减小为0。该三角形单元的半宽为a，单元载荷的公式为

（p（t）=p_0/a（a-|t|），|t|≤a  ，@q（t）=q_0/a（a-|t|），|t|≤a  。）      （5）

用x表示半平面内响应点（x，z）与三角形单元底边中点在t轴方向的相对距离，z表示响应点在z方向的深度，将表面上（-a，0）（a，0）、O到（x，z）的距离用d_1 、d_2 、d表示

{（d_1^2=〖（a-x）〗^2+z^2   ， @d_2^2=〖（a+x）〗^2+z^2   ，@d^2=x^2+z^2   。）┤    （6）

将式（5）代入式（1），经过一系列积分运算与简化，得三角形分布法向载荷p_0作用下各应力分量为

{（σ_x=-p_0/πa [（a-x）arctan （a-x）/z+（x+a）arctan （a+x）/z ├ -2xarctan x/z+2zln d^2/（d_1 d_2 ）]   ，┤@σ_z=-p_0/πa [（x-a）arctan （x-a）/z┤+（x+a）arctan （a+x）/z ├ -2xarctan x/z]   ，@τ_xz=（zp_0）/πa [arctan （a+x）/z+arctan （x-a）/z-2arctan x/z]   。）┤   （7）

同理，三角形分布切向载荷q0作用下半平面内任意一点H（x，z）处各应力分量为

{（σ_x=q_0/π {2ln d_1/d_2 +2x/a ln d^2/（d_1 d_2 ）+3z/a （2arctan x/z ├ ├ -arctan （a+x）/z-arctan （a-x）/z） }   ，┤ ┤@σ_z=（zq_0）/πa （arctan （a+x）/z+arctan （x-a）/z-2arctan x/z）   ，@τ_xz=-q_0/πa [（a-x）arctan （a-x）/z+（x+a）arctan （a+x）/z ├ -2xarctan x/z+2zln d^2/（d_1 d_2 ）] ┤   。）┤  （8）

需要指出的是，式（7）～（8）与文献[15]相应的公式不同，本文公式更加清晰地显示出了场点和源点之间的作用关系，采用本文的形式可以更好地利用离散卷积的性质，便于后续的加速计算。

3 数值求解

3.1 三角形、均布载荷离散方法

对任意分布的载荷用一系列重叠等宽的三角形单元进行离散，如图4所示。

将载荷划分为n个单元，从左到右编号依次从1递增到n，其第j个单元底边中点位置为（x_j，0），用x_ij表示任意深度z=k的第j个三角形单元与响应点（x_i，z_k）在x方向的相对距离|x_i-x_j |，i表示计算区域内的第i个单元。在该法向单元载荷作用下，响应点处x方向的应力为

{σ_x }_ij=-p_j/πa [（a-x_ij）arctan （a-x_ij）/z_k ┤+（x_ij+a）arctan（a+x_ij）/z_k  ├ -2xarctan x_ij/z_k +2z_k ln d^2/（d_1 d_2 ）]，   （9）

式中，

{（d_1^2=（a-x_ij ）^2+z_k^2   ，@d_2^2=（a+x_ij ）^2+z_k^2   ，@d^2=x_ij^2+z_k^2   。）┤  （10）

取應力函数的影响系数T_（j-i）为

T_（j-i）=-1/πa [（a-x_ij）arctan （a-x_ij）/z_k +（x_ij+a）arctan （a+x_ij）/z_k ┤ ├ -2xarctan x_ij/z_k +2z_k ln d^2/（d_1 d_2 ）] 。    （11）

受载半平面内任意位置点（x_i，z_k）在n个三角形载荷单元的叠加作用下，其x方向的应力可表示为：

σ_（x_i ）=∑_（j=1）^n?T_（j-i）  p_j 。  （12）

同理，其他方向以及切向力作用下的应力均可表示为相同的形式。

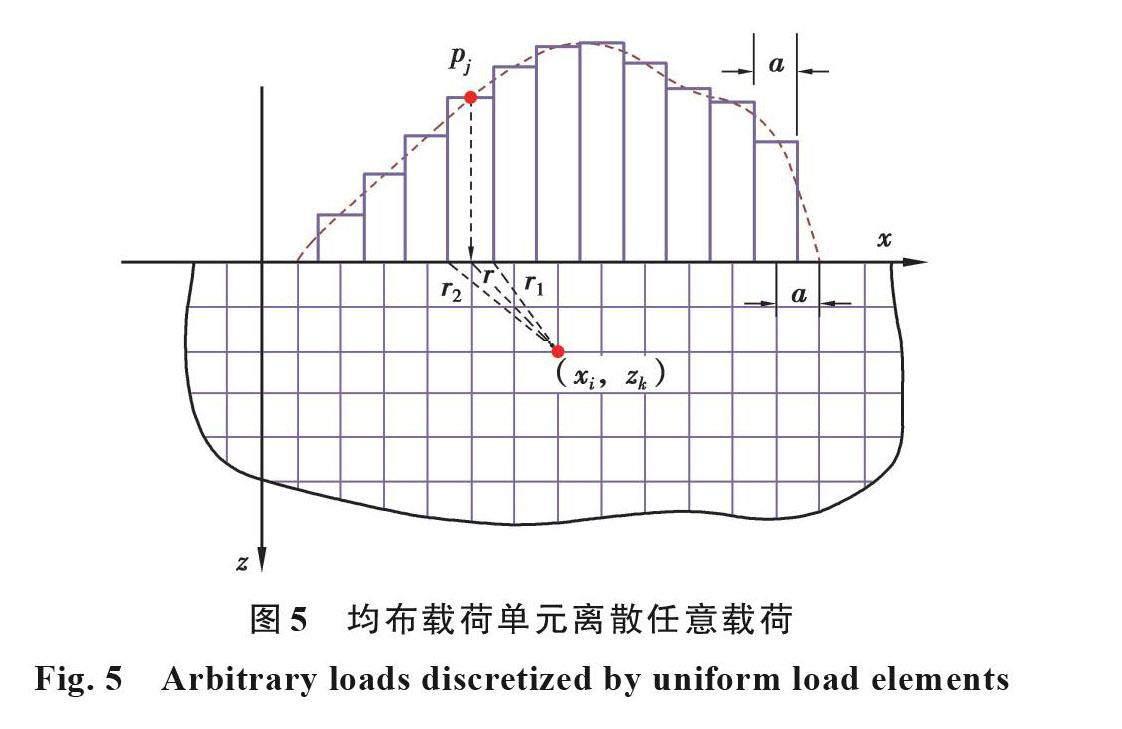
均布载荷单元离散如图5所示，叠加思想过程与三角形离散过程相同。

3.2 离散卷积快速傅里叶变换求解

本文研究的问题可以利用“激励-响应”机制求解，弹性基体次表层的各应力分布，都是表面上n个三角形单元叠加作用下的响应，可以写成如下卷积形式，其中*表示卷积

（f *g）（x）=f（x）*g（x）=∫_（-∞）^∞?〖f（α）〗 g（x-α）dα  。     （13）

对于所有变量都仅与相对距离相关的连续系统，可以利用快速傅里叶变换来解决计算规模庞大的复杂问题。为方便编程计算，将半平面离散为合适尺寸的均布载荷单元，如图5所示。在载荷作用范围内，深度为z的平面上取相同数量n个均布载荷区域的节点，利用式（12），该n个节点的应力值可表示为如下应力影响矩阵T_（j-i）与载荷矩阵P_j的乘积，即

[（σ_（x_1 ）@σ_（x_2 ）@?@σ_（x_n ） ）]=[（T_0&T_（-1）&…&T_（1-n）@T_1&T_0&…&T_（2-n）@?&?&?&?@T_（n-1）&T_（n-2）&…&T_0 ）][（p_1@p_2@?@p_（n-1）@p_n ）] 。      （14）

式（14）影响矩阵为n阶Toeplitz矩阵，为引入FFT算法，需将影响矩阵扩充为循环矩阵。现取其首列、首行来构造包卷循环a_2n，

a_2n=[（T_0&T_1&…&T_（n-1）&（0&T_（1-n）&…）&T_（-1） ）]^T 。     （15）

将这个包卷循环作为循环矩阵C_2n的第一列，利用循环矩阵的性质来将矩阵补充完整。载荷矩阵P_n通过在第n项后补n个0，将其扩充成为2n项，得到P_2n。则扩充后的应力分量表示为

σ_2n=C_2n P_2n=C_2n [（P_n@0_n ）]=[（T_（j-i） P_n@Θ）]=[（σ_n@Θ）] ，  （16）

式中，Θ表示多余项，与求解无关，原本需要求解的应力矩阵就是扩充运算后σ_2n的前n项。利用循环矩阵如下性质

C_2n=F_2n^（-1） diag（F_2n a_2n）F_2n 。      （17）

式中，F_2n是离散傅里叶矩阵，diag函数用于构造一个对角矩阵，式（17）代入式（16）得

σ_2n=C_2n P_2n=F_2n^（-1） diag（F_2n a_2n）F_2n P_2n 。     （18）

式（18）两边左乘离散傅里叶矩阵得

F_2n σ_2n=F_2n F_2n^（-1） diag（F_2n a_2n）F_2n P_2n=diag（F_2n a_2n）F_2n P_2n  。      （19）

由式（19）可知，求解扩展后的应力矩阵时只需对式（15）以及载荷矩阵P_2n做傅里叶变换后对应项相乘，再对整体做一次逆变换即可：

σ_2n=F_2n^（-1） [diag（F_2n a_2n）F_2n P_2n] 。  （20）

最终取σ_2n的前n项即所求节点的应力矩阵。引入离散傅里叶矩阵可以细化运算结构，把原始高阶矩阵运算，依次分解成一系列低阶矩阵运算。充分利用离散傅里叶变换所具有的对称性质和周期性质，并进行适当组合，就可以去除重复计算，减少计算过程中的乘法运算，让整体的运算结构更清晰简便，这就是快速傅里叶变换应用在此類“激励-响应”系统中起到加速效果的机理。而且在具体运用中涉及到的计算规模越大，FFT算法在计算效率上的优越性就越显著。

4 结果与讨论

4.1 三角形单元离散数值解验证

为验证三角形单元离散数值解法的有效性，现引入赫兹型的接触载荷，如式（21）所示，

P（x）=P_0 √（1-x^2/r^2 ） 。  （21）

切向载荷大小是法向载荷的0.3倍，载荷半径r为5 mm，中心轴为z轴，P_0为100 MPa。第j个三角形离散单元的顶点处对应的法向载荷为

P（j）=P_0 √（1-〖x_j〗^2/r^2 ） 。     （22）

将接触应力分为40个离散单元，每个单元半宽a=0.25 mm，将受载半平面用0.25 mm×0.25 mm的正方形单元进行离散，如图6所示。

利用Fortran编程计算，将赫兹型载荷解析解得到的结果与相同接触应力作用下三角形单元离散方法得到的各应力分量进行对比验证。

图7是法向力作用下深度为1 mm时，x从-4 mm到4 mm各节点上三角形离散数值解与解析解各应力分量对比。图7中，3条曲线分别是通过解析法计算得出的σ_xx 、σ_zz 、σ_xz值，相同颜色散点是三角形单元离散数值方法计算得出的对应的应力值。图8是切向力作用下2种方法得到的各应力值对比。观察可知，此种方法得到的数值解与解析解无论在法向还是切向接触应力的作用下，深度为1 mm处各应力分量都能保持较高的吻合度。

为验证本文数值算法的有效性，对比验证了受法向与切向载荷共同作用且接触平面下深度z分别为0.25、1.25、2.25 mm时，解析解和数值解得到的各节点应力响应，如图9～11所示。

在法向与切向载荷共同作用下，三角形离散数值方法求得的不同深度各应力分量（散点）数值解也可以与解析解（曲线）保持很好的吻合度。图10中z方向应力值在z=1.25时，偏差相对较大，经计算，该组数据中数值解与解析解的平均相对误差实际只有0.123%，這并不影响本数值方法的有效性。经计算，在总宽10 mm，单元宽度为0.25 mm的情况下，受载半平面内各点的应力分量数值解和解析解的相对误差平均值仅为0.048 7%。因此，利用一系列重叠等宽的三角形单元离散表面接触应力，进行数值计算是可行的。

4.2 三角形单元离散与均布载荷单元离散数值解对比

利用3.1节中提到的数值计算方法，用均布载荷单元离散法向和切向接触应力，通过Fortran编程计算，得到受载半平面内各节点应力场数值解。将接触平面深度z=0.25 mm处的各节点均布载荷单元离散数值解、三角形单元离散数值解与赫兹解析解的相对误差作对比，如图12～13所示。

由图12～13观察可知，在相同的单元宽度和单元数量下，用三角形单元进行离散比用均布载荷单元离散得到的各应力分量数值解与解析解的相对误差更小。为更全面地观察2种离散方法的准确性，用各应力分量换算得到Mises屈服应力，将数值方法得到的在接触面下z=1 mm时，x从-3 mm到3 mm的一系列节点上Mises屈服应力相对解析解的误差值进行对比，得到结果如表1所示。

由表1分析可知，均布载荷离散数值解与相同位置Mises应力解析解的相对误差比三角形离散数值解与相同位置Mises应力解析解的相对误差大一倍。这验证了三角形单元离散的方法由于各个单元之间不存在跳跃式的间断，而是相互重叠，使单元与单元之间过渡更加平稳，与原本光滑连续的接触应力实际作用情况更为接近，所以在计算精度上要优于普通的均布载荷离散方法。

4.3 DC-FFT与直接计算效率对比

在数值离散方法中，离散单元越精细，数量越多，就越会得到更接近真实解的结果，但这也会带来极大的计算量，所以采用更为高效的计算方法来提高运算效率非常必要。DC-FFT方法可以将原本N阶离散傅里叶变换的时间复杂度从O（N^2）降到O（NlogN），其中О表示算法复杂度的阶次范畴，运算的复杂度越高，DC-FFT方法节约的运算成本就越大。为了对比本文算法和直接计算方法在计算效率上的具体差距，分别用这2种方法求解法向载荷作用下半平面深度为1 mm的一系列节点的x方向应力，通过改变计算的节点数量，对比2种计算方法所需CPU时间，得到结果如表2所示。

由表2可知，计算2^13个节点的应力值时，2种方法计算耗时相差184倍。随着计算量增加，可以看到，节点数从2^13个增加到2^18个的过程中，直接计算所需要的CPU时间急剧增加，而用FFT计算所需的时间却始终不到0.1 s，在计算量增加到2^18个节点时，DC-FFT方法所需时间刚好超过0.1 s，而直接计算消耗的计算时间已经接近1 h，从比率上看两者时间更是相差34 957倍。以这样的趋势和DC-FFT方法的特性上看，在需要精确计算基体更大区域范围内各应力分量时，由于计算规模急剧增加，2种方法所消耗的计算资源差距也会更加明显。因此，DC-FFT方法是能稳定高效地得到相当高精度数值解的优质算法。

5 结  论

提出了一种高效的数值化计算方法，用以快速求解复杂接触应力情况下基体内部应力场。主要得到如下结论：

1）分别获得了在三角形和分段均布接触载荷分布下，基体内任意点应力的显式解析解；

2）通过与快速傅里叶变换算法相结合，分别构建了基于三角形和分段均布接触载荷单元的高效计算方案；

3）相比于分段均布载荷的矩形离散算法，在相同单元数和单元宽度下，基于三角形接触载荷单元的离散算法得到的数值解更精确。

4）基于三角形接触载荷单元和离散卷积-快速傅里叶变换算法（DC-FFT）所构建的计算方案，具有优异的鲁棒性、计算效率和计算精度。

参考文献

［1］  Li Y Y， Yang Y， Li M， et al. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication[J]. Mechanical Systems and Signal Processing， 2022， 162： 108059.

［2］  Brebbia C A. The boundary element method in engineering practice[J]. Engineering Analysis， 1984， 1（1）： 3-12.

［3］  Nowell D， Hills D A. Tractive rolling of tyred cylinders[J]. International Journal of Mechanical Sciences， 1988， 30（12）： 945-957.

［4］  Ju Y， Farris T N. Spectral analysis of two-dimensional contact problems[J]. Journal of Tribology， 1996， 118（2）： 320-328.

［5］  Sun L L， Wang Q J， Zhao N， et al. Discrete convolution and FFT modified with double influence-coefficient superpositions （DCSS-FFT） for contact of nominally flat heterogeneous materials involving elastoplasticity[J]. Computational Mechanics， 2021， 67（3）： 989-1007.

［6］  Sun L L， Wang Q J， Zhang M Q， et al. Discrete convolution and FFT method with summation of influence coefficients （DCS-FFT） for three-dimensional contact of inhomogeneous materials[J]. Computational Mechanics， 2020， 65（6）： 1509-1529.

［7］  Wang Q J， Sun L L， Zhang X， et al. FFT-based methods for computational contact mechanics[J]. Frontiers in Mechanical Engineering， 2020， 6： 61.

［8］  Li Q A， Popov V L. Non-adhesive contacts with different surface tension inside and outside the contact area[J]. Frontiers in Mechanical Engineering， 2020， 6： 63.

［9］  牛睿， 萬强， 靳凡， 等. 基于共轭梯度法和快速傅立叶变换的粗糙表面微动接触数值研究[J]. 计算力学学报， 2017， 34（3）： 312-321.

Niu R， Wan Q， Jin F， et al. A numerical analysis of fretting contact with rough surface based on conjugate gradient method and fast Fourier transform[J]. Chinese Journal of Computational Mechanics， 2017， 34（3）： 312-321.（in Chinese）

［10］  Rey V， Anciaux G， Molinari J F. Normal adhesive contact on rough surfaces： efficient algorithm for FFT-based BEM resolution[J]. Computational Mechanics， 2017， 60（1）： 69-81.

［11］  Yu Y H， Suh J. Numerical analysis of three-dimensional thermo-elastic rolling contact under steady-state conditions[J]. Friction， 2022， 10（4）： 630-644.

［12］  吴桐. 粗糙表面微动接触分析[D]. 武汉： 武汉科技大学， 2019.

Wu T. Fretting contact analysis of rough surfaces[D]. Wuhan： Wuhan University of Science and Technology， 2019.（in Chinese）

［13］  帅琪琪， 陈晓阳， 陈世金， 等. 预紧方式对弹流润滑下角接触球轴承内部力学特性的影响[J]. 摩擦学学报， 2022， 42（1）： 85-94.

Shuai Q Q， Chen X Y， Chen S J， et al. Influences of preload methods on internal mechanical characteristics of angular contact ball bearings under elastohydrodynamic lubrication[J]. Tribology， 2022， 42（1）： 85-94.（in Chinese）

［14］  Zhang X， Wang Q J， He T. Transient and steady-state viscoelastic contact responses of layer-substrate systems with interfacial imperfections[J]. Journal of the Mechanics and Physics of Solids， 2020， 145： 104170.

［15］  Johnson K L. Contact mechanics[M]. Cambridge： Cambridge University Press， 1987.

（编辑  郑洁）