神经网络模型度量地形对实际行驶排放的影响

常虹 吴冬梅 张力 龚香坤 徐划龙 付明明

摘要：由于难以将行驶路线地形的影响从实际行驶排放（real driving emission，RDE）试验的其他试验边界的影响中独立出来，提出采用神经网络输入变量重要性算法以定量评估行驶路线地形试验边界对RDE试验的影响强度。以重庆地区RDE试验的37 256个数据窗口排放样本为基础，采用因子分析方法缩减数据并消除试验边界之间的信息重叠，建立神经网络模型预测污染物排放，并计算输入变量相对重要性占比。结果表明，行驶路线地形试验边界在二氧化碳（CO2）排放中起主导作用，它的相对重要性远大于行程动力学试验边界。对于一氧化碳（CO）、颗粒数量（particle number，PN）、氮氧化物（NOx）污染物排放，地形因素的影响力仍不可忽视，特别是在车辆高速行驶条件下，它对车辆行驶排放的影响与行程动力学因素大致相当。总体而言，在现有排放标准体系中，行驶路线地形试验边界对RDE试验的影响被严重低估。

关键词：实际行驶排放；排放模型；神经网络；地形；行程动力学

中图分类号：U448.213          文献标志码：A        文章编号：1000-582X（2024）01-031-10

Effect of route topography on real driving emissions based on neural network models

CHANG Hong1， WU Dongmei2， ZHANG Li2， GONG Xiangkun1，

XU Hualong1， FU Mingming2

（1. China Automotive Engineering Research Institute Co.， Ltd.， Chongqing 401122， P. R. China;

2. School of Mechanical and Automotive Engineering， Chongqing University， Chongqing 400044， P. R. China）

Abstract： It is difficult to separate the effect of route topography from that of other test boundaries in real driving emission （RDE） tests. We proposed an artificial neural network （ANN） weight method to quantitatively evaluate the impact of route topography on RDE tests. Based on 37 256 data window samples of RDE tests in Chongqing， a factor analysis method was used to reduce data and eliminate information overlap between test boundaries. Additionally， a neural network model was also established to predict pollutant emissions and calculate the relative importance of input variables. The results show that route topography significantly affects CO2 emissions， with its relative importance far exceeding that of other test boundaries. Moreover， the influence of the route topography cannot be ignored for CO， PN （particle number）， and NOx emissions， having an impact on vehicle driving emissions comparable to that of trip dynamics， especially under high-speed driving conditions. However， the existing regulatory emission standards seriously underestimate the impact of the route topography on vehicle driving emissions.

Keywords： RDE （real driving emission）; emission model; artificial neural network; route topography; trip dynamics

國内外针对车辆污染物排放设立了各种强制性法规，涉及严格的排放限值和新车必须遵守的认证测试程序[1-3]。然而，大量的研究表明，排放法规所规定的试验室标准驾驶循环缺乏车辆实际行驶状态的完整代表性[4-6]，基于试验室标准驾驶循环的车辆排放测试难以充分和准确地反映现代交通系统中车辆实际行驶状态下的真实污染物排放[7-9]。为此，欧洲和中国第六阶段机动车污染物排放标准（简称国六）强制性引入实际行驶排放（RDE）测试程序[10-11]。与试验室条件下的标准测试循环不同，RDE试验为一个受多种因素（环境条件、驾驶员行为、行驶路线地形、交通状况、有效载荷等）可变性影响的道路测试，其试验边界具有随机性和不确定性，导致RDE试验测试数据的不可重复性和试验评价结果的非一致性[6，12]。

行驶路线地形被认为是影响RDE试验的重要试验边界[13-14]。Lijewski等[15]分别在2条不同的行驶路线上对比了插电式混合动力汽车（plug-in hybrid electric vehicle，PHEV）和增程式电动车的污染物排放差异；在一条行驶路线上，增程式电动车的NOx排放低70%，而在另一条行驶路线上PHEV的NOx排放反而要低60%。Costagliola等[16]试验表明，CO2排放量与道路坡度呈正线性关系；随着道路坡度增加，NOx排放的增长呈二阶多项式规律。Faria等[17]发现在低坡度道路上的驾驶侵略性往往与CO2排放量增加较高相关。Prakash等[18]认为瞬时NOx与CO2排放之间存在强正相关，道路坡度对NOx排放所产生的影响随驾驶侵略性增加而降低。Du等[19]用2台车辆在4条不同试验线路上分别进行2次RDE试验，结果表明，不同试验线路下的比距离排放呈现显著非一致性。不同行驶线路下的2次RDE试验不可能保持相同的行程动力学特性，不同行驶线路下RDE试验所表现出的差异可能与行程动力学特性等其他试验边界条件的不一致有关。在上述研究中，不同试验测试表现出的现象和规律相差较大，多数结论不具有普遍性。由于难以将行驶路线地形的影响从RDE试验的其他影响因素中区分和独立出来，行驶路线地形试验边界对RDE试验究竟会产生何种程度的影响仍难以准确度量。

本研究中提出采用神经网络输入变量重要性度量行驶路线地形对RDE试验的影响强度。用相同试验车辆在重庆地区进行大量RDE试验测试，按照移动平均窗口法（moving average window，MAW）将所得的逐秒采样测试数据划分为数据窗口子集。考虑影响窗口污染物排放的各种因素，并将之划分为地形因素和行程动力学因素2类。对于行程动力学因素，鉴于描述变量较多且有信息重叠，采用主成分分析方法从变量群中提取共性因子，以因子得分组合替代原始变量，从而消除原始变量之间的信息重叠。在此基础上，以数据窗口的地形和行程动力学因素作为输入量，数据窗口排放因子为输出量训练神经网络模型；采用神经网络输入变量重要性算法，计算地形和行程动力学因素在窗口污染物排放中的重要性占比。研究表明，行驶路線地形因素对实际行驶排放的影响与行程动力学因素具有几乎相当的重要性，行驶路线地形试验边界对实际行驶排放的影响在RDE法规试验程序中被严重低估。

1 窗口数据

试验车辆为2018年生产的轻型汽油乘用车型，整车质量2.1 t，已有行驶里程18 000 km。试验车辆发动机的排量为2.0 L，采用缸内直喷燃油供给方式，燃油标号为92号汽油，进气方式为废气涡轮增压，尾气后处理系统配备三元催化器（TWC）和汽油机颗粒捕集器（GPF），满足国六排放标准。试验车辆动力传动系统为6AT自动变速器。车载排放测试系统为HORIBA公司生产的OBS-ONE便携式排放测试系统（PEMS）。测试系统配置全球定位系统（GPS）接收器，可以通过车辆的经度、纬度、海拔等信息计算得到车辆的速度，其位置精度在±10 m范围内。另外，测试系统通过车载诊断系统（OBD）获取发动机和车辆的数据，包括：发动机转速、发动机冷却剂温度、节气门位置、进气质量流量、进气压力等；通过测量排气流量管的压力差、排气压力和温度计算出排气流量。测试系统还配置大气压力传感器、环境温度和湿度传感器，通过结合GPS输出信息，获取试验过程中的环境信息（经度、纬度、海拔、温度、大气压力）。遵照RDE法规试验程序，试验车辆分别在重庆江津、北碚、渝北等区域完成10次RDE试验。其中，车辆载荷（测试质量）、环境条件（平均海拔、温度）、行驶线路（市区、市郊和高速路段的里程与平均车速，起点和终点的海拔差与行程累计正海拔增量）、燃油和润滑油以及路段行程动力学特性等均遵循RDE法规试验程序的要求。

采用移动平均窗口法将RDE试验连续逐秒采样的测试数据划分为一系列数据子集，并称之为数据窗口。划分数据窗口时，向前（或向后）的移动步长与PEMS数据取样周期一致，且数据窗口的时间长度应恰好使该数据窗口中CO2排放质量等于该车辆在全球统一轻型车辆测试循环（worldwide light-duty vehicle test cycle， WLTC）的CO2排放质量的一半[20]。首先，根据数据窗口的平均车速将数据窗口划分为市区、市郊和高速窗口。其中，平均车速小于45 km/h的窗口为市区窗口，平均车速大于或等于45 km/h且小于80 km/h的窗口为市郊窗口，平均车速大于或等于80 km/h且小于145 km/h的窗口为高速窗口。在此基础上，计算表征数据窗口行程属性的相关参数，包括平均车速（v）、v?apos[95] （车速与大于0.1 m/s2正加速度乘积的95百分位）、VSPpos[95]（整车比功率升序排列的第95个百分位值）、相对正加速度（RPA）、平均正加速度（MPA）、累计正海拔增量等。然后，再将计算所得特征参数作为行程属性赋予数据窗口，使数据窗口具有路段属性，从而将试验逐秒采样数据转化为类行程数据。窗口行程数据是后续统计分析的样本对象。

图1给出了数据窗口的地形特征的数据统计。

图中的累计正海拔增量数据分段序号对应的是将累计正海拔增量按200 m/（100 km）间距划分的10个数据段；纵坐标为各个累计正海拔增量数据段对应的窗口数量。其中，1～6号数据段的累计正海拔增量介于0～1 200 m/（100 km）之间，在RDE法规试验程序所规定的限值范围之内；7～10号数据段的累计正海拔增量则大于RDE法规试验程序所规定的上限值1 200 m/（100 km）。市区窗口样本集中有1/3（约5 000个）数据窗口的累计正海拔增量超过了法规上限值。市郊窗口样本集中约有2 000个数据窗口的累计正海拔增量超过了法规上限值，但累计正海拔增量接近法规限值的窗口数量仍较多，在1 000～1 200 m/（100 km）数据段（6号数据段）的窗口数量超过4 000个。高速窗口样本集中累计正海拔增量超过法规限值的窗口数量则明显减少，道路相对平缓，窗口数量最多的数据段为600～800 m/（100 km）的数据段（4号数据段）。数据窗口样本集包含了具有各种不同行驶路线地形特征的大量行程测试数据。

2 数据缩减

选取影响RDE试验的试验边界条件，包括数据窗口的v、v?apos[95]、VSPpos[95]、RPA、MPA以及累计正海拔增量，将这些影响窗口污染物排放的试验边界条件划分为地形因素和行程动力学因素两类。数据窗口地形属性的描述变量为行驶路线的累计正海拔增量，数据窗口行程动力学属性的描述变量包括v、v?apos[95]、VSPpos[95]、RPA和MPA。对于行程动力学因素，各个描述变量之间有一定相关性，解释为各个描述变量反映的主题信息有一定的重叠，这种重叠会干扰变量影响力的评估。为此，采用因子分析法将行程动力学描述变量综合为数量较少的成分因子，并通过构造适当的价值函数（根据方差百分比）进一步把行程动力学的低维描述转化成一维描述，从而消除行程动力学描述变量之间的信息重叠。在此基础上，将数据窗口样本集中的窗口污染物排放、窗口累计正海拔增量和窗口行程动力学因子用于构造和训练神经网络模型，通过利用神经网络变量重要性算法计算输入变量的相对重要性。

因子分析是从高维数据的变量群中提取共性因子并将原始变量表示成少数公共因子和特殊因子的组合的多元统计方法[21]。因子分析通过建立因子荷载矩阵，获取原始变量的因子表达式的系数；通过因子得分矩阵得到因子的线性组合，并以因子替代原始变量，从而将原高维数据系统以较高的精度转换成低维数据系统，达到对事物进行分类并且综合评价的目的[22]。为此，首先针对试验样本数据集分别采用KMO（Kaiser-Meyer-Olkin）法和Bartlett法进行适用性检验（检验之前对样本数据进行标准化处理）。市区、市郊和高速窗口样本集经检验均满足进行因子分析的条件。

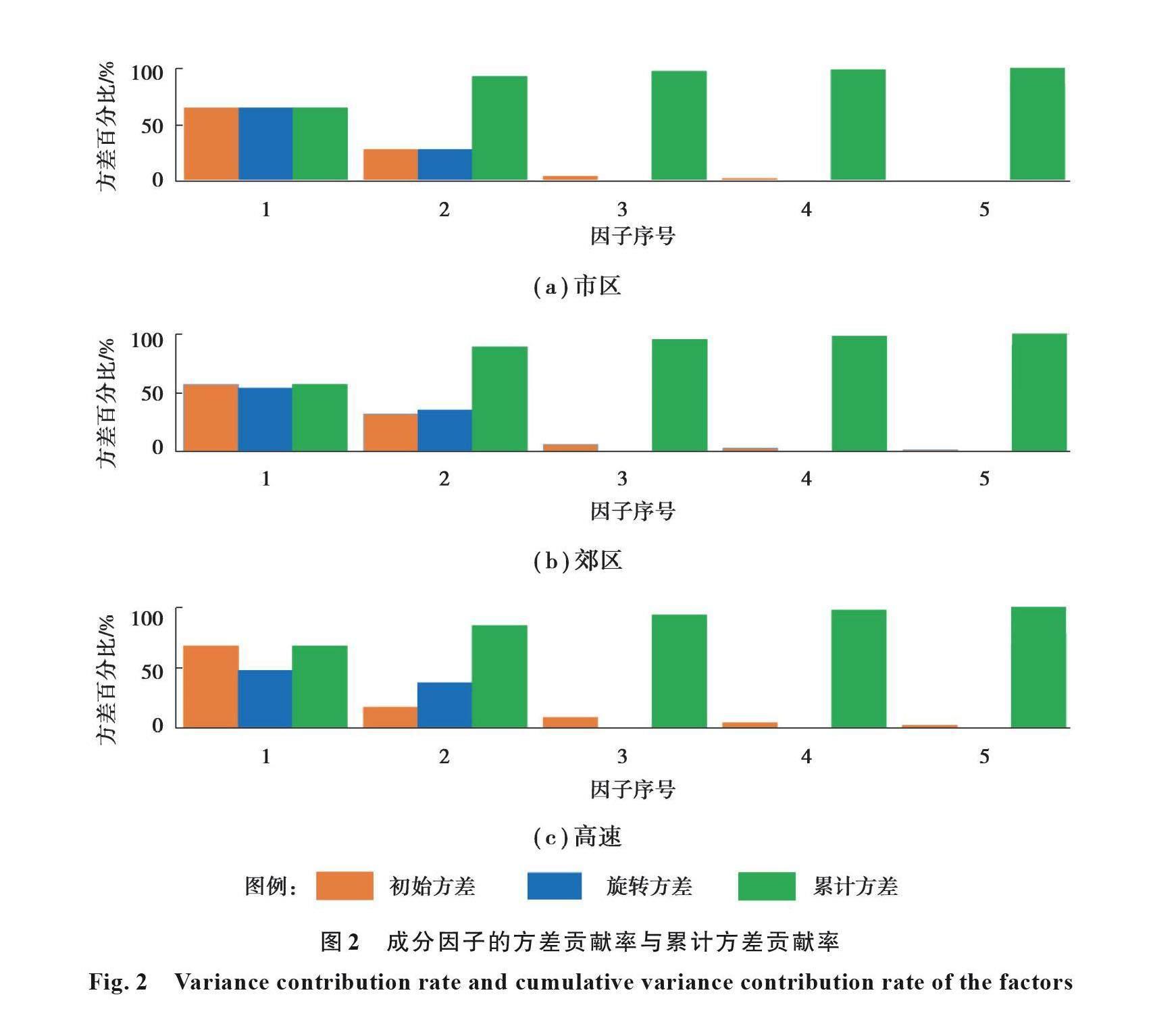
因子分析通过坐标变换将原始变量转换为另一组不相关的变量（因子），再求取相关系数矩阵的特征值和相应的标准正交的特征向量，根据相关系数矩阵的特征值计算成分因子的方差贡献率与累计贡献率，如图2所示。在市区窗口样本集中，前2个因子的累计方差贡献率达到92.7%，这表明这2个因子基本包含原始变量所代表的全部信息，被称为成分因子。同样，市郊窗口样本集中前2个分量的累计方差贡献率为89.2%，高速公路窗口样本集中前2个分量的累计方差贡献率为84.9%。因此，在每一个数据窗口样本集中，可以使用由5个原始变量线性组合而成的2个成分因子整体描述试验车辆的行程动力学状态，从而将试验数据空间从5维降至2维。这一处理过程中所产生的信息损失是少量的。

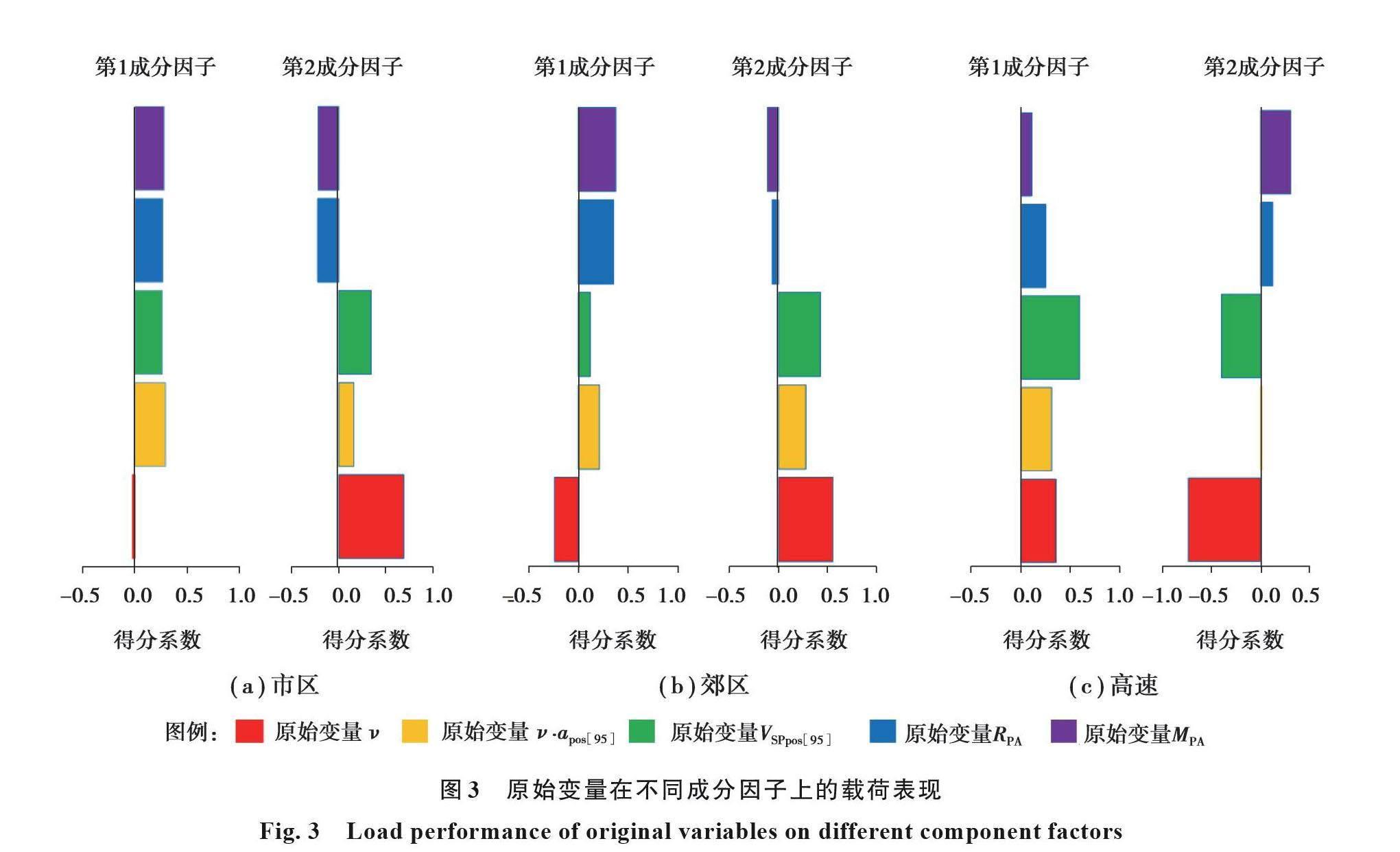
为确定所得的2个成分因子的实际意义，采用方差最大正交旋转原则（使成分因子的相对负荷的方差之和最大，且保持原有的成分因子的正交性和公共方差总和不变）进行因子旋转，找出2个成分因子与5个原始变量的关系。对每一个窗口样本集采用回归法得到原始变量在不同成分因子上的载荷，即因子得分。图3为3组数据窗口样本集原始变量的因子得分系数，据此将成分因子表示为原始变量的线性组合。以市区窗口样本集为例，第1成分因子可以表示为v、v?apos[95]、VSPpos[95]、RPA、MPA的线性组合，对应的线性组合系数分别为0.004、0.295、0.264、0.268、0.283；第2主成分也可以表示为这些原始变量的线性组合，对应的线性组合系数分别为0.689、0.159、0.342、0.224、0.219。在此基础上，根据图2中的旋转方差贡献率将2个成分因子线性加权组合构成一个新的综合变量（加权系数分别为64.7/92.7和28.0/92.7）。该变量可以从总体效果上替代原始变量用于反映市区窗口样本集中窗口行程动力学特性，称为市区窗口样本集的行程动力学因子。图4给出了市区窗口行程动力学因子与原始变量的比较，图中的红色线条为行程动力学因子，黑色线条为原始变量。行程动力学因子是原始变量v、v?apos[95]、VSPpos[95]、RPA、MPA的综合反映，它与VSPpos[95]、v?apos[95]有较好的相似性。按此方法，同样可以构造市郊和高速窗口样本集的行程动力学因子。至此，窗口数据样本集中边界条件的6个字段（v、v?apos[95]、VSPpos[95]、RPA、MPA以及累计正海拔增量）描述被缩减至2个字段（行程动力学因子和累计正海拔增量）描述。

3 模型分析

分別针对市区、市郊和高速的数据窗口样本集构建CO2、CO、NOx、PN排放的神经网络模型。模型为前馈、监督学习的多层感知器（MLP）网络，使用2个隐藏层（不同污染物排放模型的隐藏层神经元个数根据模型的观测预测情况进行不同的设置），隐藏层激活函数采用双曲正切；输入变量为数据窗口的累计正海拔增量和经主成分分析得到的数据窗口行程动力学因子，输出目标为数据窗口的污染物排放因子。分别针对市区、市郊、高速窗口数据样本集，随机选择各组数据集中70%的数据作为模型训练样本，30%的数据作为模型测试样本。图5给出了神经网络模型对市区窗口污染物排放的观测和预测（黑色线条为观测数据，红色为预测数据）。图中，神经网络模型计算的预测值与作为观测的测试数据展现了良好的一致性。其中，CO2、CO、NOx、PN污染物排放的观测值和预测值的决定系数R2分别达到0.881、0.932、0.750和0.978。可见，经模型训练，神经网络自动逼近正确的模型结构，正确映射了数据结构中隐含的因变量和自变量的关系形式，充分揭示了累计正海拔增量和行程动力学因子对实际行驶污染物排放的主导性影响作用。

基于神经网络模型所表达的窗口污染物排放与累计正海拔增量、行程动力学因子之间的因果关系，采用神经网络敏感性分析（sensitivity analysis）方法定量评估神经网络模型中2个输入变量对输出目标的重要性。敏感性分析是一种定量描述模型输入变量对输出目标的重要性程度的方法，它通过计算归因于输入变量的输出目标的方差变化确定该输入变量对输出目标的影响程度[23]。对于输出目标为Y，输入变量为X1、X2、…、Xk的神经网络模型，输入变量敏感性的测量如下：

S_i=（V_ar （E（Y├|X_i ┤ ） ））/（V_ar （Y） ），i=1，2，…，k。      （1）

式中：Si为敏感性系数；Var为方差算子，V_ar （Y）为输出目标的无条件方差；E为期望算子，E（Y├|X_i ┤ ）为除去变量Xi影响的Y的条件期望[24-25]。

靈敏度系数为输入变量相对于输出目标的一阶灵敏度度量，如果输入变量X1、X2、…、Xk的集合是正交或独立的，并且模型是可加的，则它是准确的。在正交情况下，也可以较容易地通过蒙特卡罗方法计算输入变量空间中的多维积分以直接估计式（1）中的条件方差。前述因子分析就是为尽量满足输入变量独立性条件所进行的数据处理。将灵敏度系数归一化处理即得到

_i=S_i/（∑_（j=1）^k?S_j ），i=1，2，…，k。    （2）

式中，VIi即为输入变量相对于输出目标的重要性占比。图6中给出了不同隐藏层节点数下获取的地形因素重要性占比。

图6中对同一组样本数据使用了不同的神经网络结构进行地形因素重要性占比的计算以确保计算结果的稳定性。对于CO2排放而言，不同神经网络结构情况下地形因素重要性占比的变化区间在市区路段为51%～62%，在市郊路段为62%～69%，在高速路段为77%～79%。就CO污染物排放而言，不同神经网络结构情况下地形因素重要性占比的变化区间在市区路段为20%～29%，在市郊路段为45%～52%，在高速路段为44%～51%。对于PN污染物排放，不同神经网络结构情况下地形因素重要性占比的变化区间在市区路段为21%～31%，在市郊路段为19%～26%，在高速路段为30%～38%。就NOx污染物排放而言，不同神经网络结构情况下地形因素重要性占比的变化区间在市区路段为33%～40%，在市郊路段为38%～43%，在高速路段为40%～52%。总体而言，神经网络结构的差异不会导致地形因素重要性占比计算值大幅度变化。

对不同神经网络结构的地形重要性占比数据进行统计平均，平均值即可用于评估行驶路线地形因素的影响强度。图7对比性给出了地形因素和行程动力学因素对染污物排放的影响力。图中可见，CO2排放与地形因素密切相关，地形因素在CO2排放中一直是主导因素。地形因素重要性占比在市区路段为57%，在市郊路段为65%，在高速路段达到78%。随车速增加，地形因素对CO2排放的影响越来越具有决定性。对于CO排放，地形因素的占比在市区路段为25%，在市郊路段为48%，在高速路段为47%；在市郊和高速路段，地形因素对CO排放的影响不可忽视，地形因素的影响与行程动力学因素基本相当。对于PN污染物排放，地形因素的重要性占比在市区路段为22%，在市郊路段为21%，在高速路段为32%；相对于行程动力学因素而言，地形因素的影响是次要的，在PN排放中起主导影响的还是行程动力学因素。就NOx污染物排放，地形因素的重要性占比在市区路段为38%，在市郊路段为41%，在高速路段为48%；可见，地形因素的影响同样不可忽视。从整体看，从市区路段至高速路段，随着车辆行驶速度增加，地形因素与对污染物排放的影响呈增加的趋势。

4 结束语

1）神经网络变量重要性算法定量给出行驶路线地形边界条件对实际行驶排放的影响力度。相对于行程动力学，行驶路线地形因素在CO2排放中起主导作用；随车速增加，地形因素对CO2排放的影响更具有决定性，它的重要性占比达到近80%。对于CO、NOx污染物排放，地形因素的影响力仍不可忽视，特别是在车辆高速行驶条件下，它对实际行驶排放所产生的影响与行程动力学大致相当。相对而言，地形因素对PN排放的影响不如行程动力学因素所具有的重要性，它的影响力是次要的，但其重要性占比也可达30%左右。总体而言，行驶路线地形因素对实际行驶排放的影响与行程动力学因素具有几乎相当的重要性。

2）目前行驶路线地形对实际行驶排放的影响被严重低估。现今车辆排放法规体系（包括WLTC等标准测试循环和RDE试验程序）并没有将行驶路线地形作为具有重要影响的试验边界加以充分考虑并进行详细设计（仅有累计正海拔增量上限值设置）。在此标准体系下，山地城市承受较平原地区更严重的污染物排放的事实容易被掩盖。考虑到山区（山地、丘陵和相对崎岖的高原）约占中国国土面积的2/3，未来RDE试验排放标准至少应推进累计正海拔增量下限值的设置，以敦促车辆制造企业重视所生产车辆在山地城市地形条件下的排放控制。

参考文献

［1］  Franco V， Kousoulidou M， Muntean M， et al. Road vehicle emission factors development： a review [J]. Atmospheric Environment， 2013， 70： 84-97.

［2］  Anenberg S C， Miller J， Injares R M， et al. Impacts and mitigation of excess diesel related NOx emissions in 11 major vehicle markets [J]. Nature， 2017， 545 （7655）： 467-471.

［3］  Frey H C， Zhang K， Rouphail N M. Fuel use and emissions comparisons for alternative routes， time of day， road grade， and vehicles based on in-use measurements [J]. Environmental Science Technology， 2008， 42（7）： 2483-2489.

［4］  Hooftman N， Messagie M， Van M J， et al. A review of the European passenger car regulations–real driving emissions vs local air quality [J]. Renewable Sustainable Energy Reviews， 2018， 86： 1-21.

［5］  Weiss M， Bonnel P， Kühlwein J， et al. Will Euro 6 reduce the NOx emissions of new diesel cars？–insights from on-road tests with portable emissions measurement systems （PEMS） [J]. Atmospheric Environment， 2012， 62： 657-665.

［6］  Suarez-Bertoa R， Valverde V， Clairotte M， et al. On-road emissions of passenger cars beyond the boundary conditions of the real-driving emissions test [J]. Environmental Research， 2019， 176： 108572.

［7］  Pavlovic J， Ciuffo B， Fontaras G， et al. How much difference in type-approval CO2 emissions from passenger cars in Europe can be expected from changing to the new test procedure （NEDC vs. WLTP）？ [J]. Transportation Research Part A： Policy， 2018， 111： 136-147.

［8］  Kousoulidou M， Fontaras G， Ntziachristos L， et al. Use of portable emissions measurement system （PEMS） for the development and validation of passenger car emission factors [J]. Atmospheric Environment， 2013， 64： 329-338.

［9］  Sileghem L， Bosteels D， May J， et al. Analysis of vehicle emission measurements on the new WLTC， the NEDC and the CADC[J]. Transportation Research Part D： Transport and Environment， 2014， 32： 70-85.

［10］  Giechaskiel B， Vlachos T， Riccobono F， et al. Implementation of portable emissions measurement systems （PEMS） for the real-driving emissions （RDE） regulation in Europe [J]. Journal of Visualized Experiments， 2016， 118： e54753.

［11］  中華人民共和国环境保护部. 轻型汽车污染物排放限值及测量方法（中国第6阶段）： GB 18352.6—2016 [S]. 北京： 中国标准出版社， 2016.

Ministry of Ecology and Environment of the Peoples Republic of China. Limits and measurement methods for emissions from light-duty vehicles （China VI）： GB18352.6—2016 [S]. Beijing： China Standard Press， 2016. （in Chinese）

［12］  Varella R A， Faria M V， Mendoza-Villafuerte P， et al. Assessing the influence of boundary conditions， driving behavior and data analysis methods on real driving CO2 and NOx emissions [J]. Science of the Total Environment， 2019， 658： 879-894.

［13］  Wyatt D W， Li H， Tate J E. The impact of road grade on carbon dioxide （CO2） emission of a passenger vehicle in real-world driving [J]. Transportation Research Part D： Transport and Environment， 2014， 32： 160-170

［14］  Gallus J， Kirchner U， Vogt R， et al. Impact of driving style and road grade on gaseous exhaust emissions of passenger vehicles measured by a portable emission measurement system （PEMS） [J]. Transportation Research Part D： Transport and Environment， 2017， 52： 215-226.

［15］  Lijewski P， Kozak M， Fuc P， et al. Exhaust emissions generated under actual operating conditions from a hybrid vehicle and an electric one fitted with a range extender [J]. Transportation Research Part D： Transport and Environment， 2020， 78： 102183.

［16］  Costagliola M A， Costabile M， Prati M V. Impact of road grade on real driving emissions from two Euro 5 diesel vehicles [J]. Applied Energy， 2018， 231： 586-593.

［17］  Faria MV， Duarte G O， Varella R A， et al. How do road grade， road type and driving aggressiveness impact vehicle fuel consumption？ assessing potential fuel savings in Lisbon， Portugal [J]. Transportation Research Part D： Transport and Environment， 2019， 72： 148-161

［18］  Prakash S， Bodisco T A. An investigation into the effect of road gradient and driving style on NOx emissions from a diesel vehicle driven on urban roads [J]. Transportation Research Part D： Transport and Environment， 2019， 72： 220-231.

［19］  Du B C， Zhang L， Zou J， et al. Investigating the impact of route topography on real driving emission tests based on large data sample at data window level [J]. Science of the Total Environment， 2022， 809： 151133.

［20］  Chen L J， Du B C， Zhang L. et al. Analysis of real-driving emissions from light-duty gasoline vehicles： a comparison of different evaluation methods with considering cold-start emissions [J]. Atmospheric Pollution Research， 2021， 12： 101065.

［21］  张尧庭， 方开泰.多元统计分析引论 [M]. 北京： 科学出版社， 1982.

Zhang Y T， Fang K T. Introduction to multivariate statistical analysis [M].Beijing： Science Press，1982. （in Chinese）

［22］  Anderson T W. An introduction to multivariate statistical analysis[M]. 3rd ed. New York： John Wiley， 2003.

［23］  Borgonovo E， Plischke E. Sensitivity analysis： a review of recent advances [J]. European Journal of Operational Research， 2016， 248： 869-887.

［24］  Saltelli A. Making best use of model evaluations to compute sensitivity indices [J]. Computer Physics Communications， 2002， 145（2）： 280-297.

［25］  Saltelli A， Annoni P， Azzini I， et al. Design and estimator for the total sensitivity index [J]. Computer Physics Communications， 2010， 181（2）： 259-270.

（編辑  罗敏）