揭示2023年上海卷第21题本质

胡晓洁

1 题目：2023年上海卷第21题

已知f（x）=ln x，取点（a1，f（a1））过其作曲线y=f（x）的切线交y轴于点（0，a2），取点（a2，f（a2））过其作曲线y=f（x）的切线交y轴于点（0，a3），若an≤0则停止，以此类推，得到数列{an}.

（1）若正整数m≥2，证明：am=ln am－1－1；

（2）[JP3]若正整数m≥2，试比较am與am－1－2的大小；

（3）若正整数k≥3，是否存在k使得a1，a2，……，ak依次成等差数列？若存在，求出k的所有取值；若不存在，试说明理由.

2 分析与思维导图

2.1 思维分析

本题从导数与数列的综合运用出发，考查学生求切线方程、构造函数证明不等式、等差数列性质的应用以及方程有解问题的解决能力，体现了数学抽象、逻辑推理、数学运算等核心素养.本题的题干是由函数图象的切线与y轴相交，交点的纵坐标经过递推得到一个数列.递推的过程和利用牛顿法求方程的解类似.数列在题目中更多是起到背景和提示作用，[JP3]本质上还是解决函数与导数的问题.本题作为上海卷的压轴题，有较大的思维量，突出考查了数学抽象和逻辑推理核心素养.

第（1）问证明数列的递推关系，本质上考查求函数的切线方程，要求学生理解题目中的递推关系.本题对学生在给定情境下分析数学问题的能力有较高的要求.

第（2）问比较大小，常用办法是将要比较的对象化成同一变量后作差.结合第（1）问的结论，可以发现本质上是考查常用不等式ln x≤x－1（ex≥x+1）的证明.本题要求学生能够结合已知结论解决问题，熟练掌握构造法证明不等式.

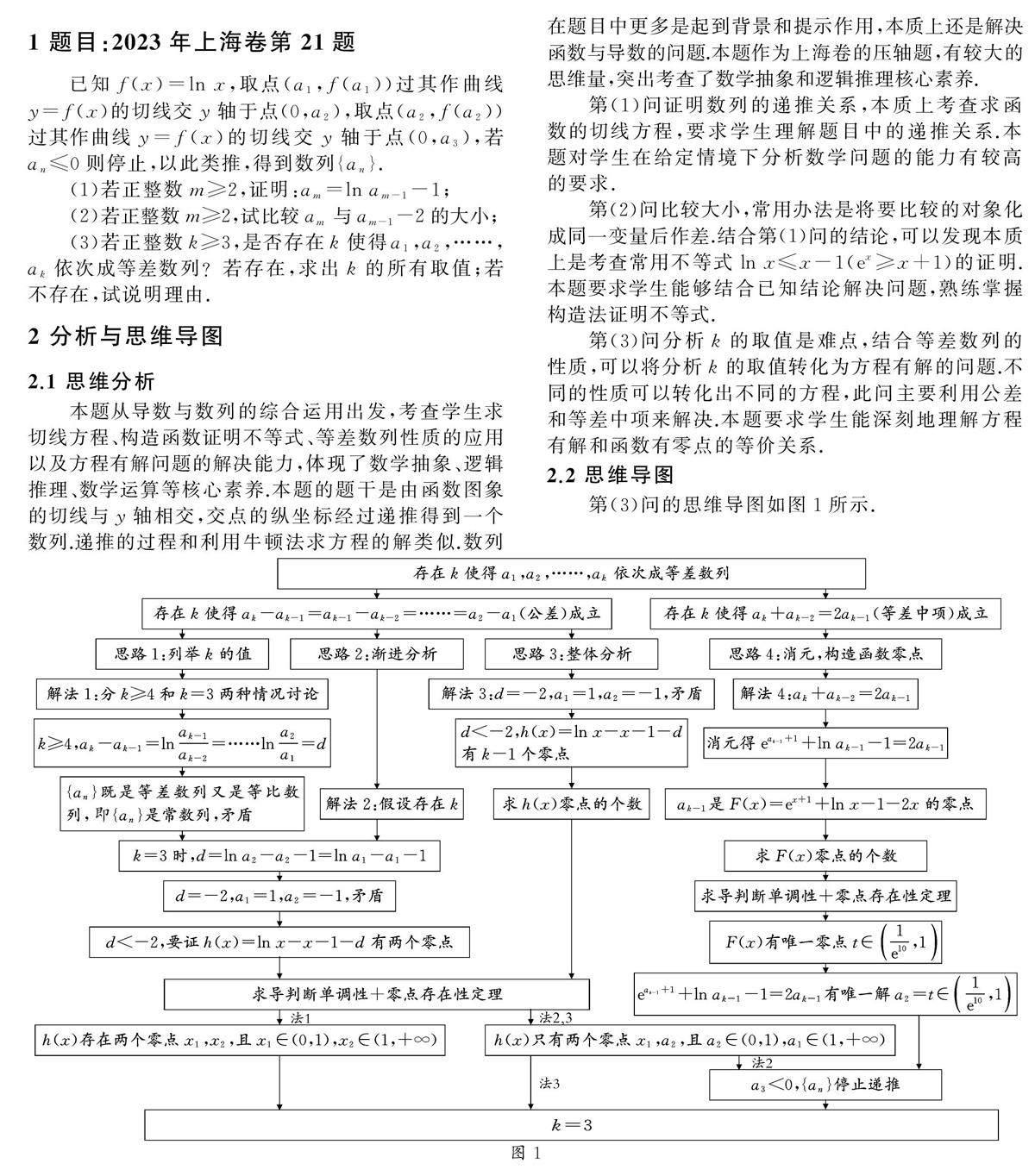
第（3）问分析k的取值是难点，结合等差数列的性质，可以将分析k的取值转化为方程有解的问题.不同的性质可以转化出不同的方程，此问主要利用公差和等差中项来解决.本题要求学生能深刻地理解方程有解和函数有零点的等价关系.