大跨径钢桥结构受横向荷载作用研究

王斌

（新疆铁道勘察设计院有限公司，乌鲁木齐 830011）

1 引言

由于钢拱桥具有美观、结构材料可高效利用等显著优点，近几十年来，钢拱桥得到了广泛的应用。 随着近年来结构分析技术和施工技术的进步，大跨径钢拱桥成为现实。 钢拱桥作为拱桥的主要结构单元，其承受的压力可能导致钢拱桥失稳，因此，结构失稳成为拱桥设计评估的主要失效模式之一[1]。 近年来， 人们对钢拱桥在不同荷载作用下的稳定性进行了大量的研究， 这些研究大多集中在垂直荷载作用下钢拱桥的稳定性分析上，相对而言，在横向荷载（如风荷载）作用下，拱桥的受力较小，所有研究都是基于结构参数完全确定的假设，通常被称为确定性分析[2]。 然而，在实际工程中，设计变量存在不确定性，这些不确定性包括几何特性（如横截面特性和尺寸）、材料的力学特性（如模量和强度）、荷载大小和分布等[3]。 因此，确定性分析不能提供关于钢拱桥屈曲荷载的完整受力信息， 应从概率的角度对拱桥的稳定性进行更合理的研究[4]。

在此基础上， 本文提出了一种估算拱桥抗风致失稳可靠性的有效方法。 在结构稳定性分析和可靠性评估模型方面，保持可行的计算水平。 本文研究了中心跨度为550 m 的大跨径钢拱桥在静风荷载作用下的安全性， 桥梁的可靠性是根据受风影响的稳定性失效来评估的。 为了评估最不利荷载组合对桥梁可靠性的影响，本文考虑了整座桥的恒载、风载和活载的荷载组合进行分析。 最后，通过灵敏度分析确定了对桥梁可靠性影响最大的随机变量。

2 工程概况

2.1 工程简介

本文选取某大跨径焊接中承式钢拱桥作为算例。 钢拱桥中心跨度为550 m，桥跨布置为100 m+550 m+100 m，双向六车道，桥的矢跨比为1/5.5。 拱肋、主梁的材料及截面性能如表1 所示。

表1 拱肋、主梁的材料及截面性能

2.2 有限元模型创建

采用有限元分析软件ANSYS 建立了钢拱桥结构的三维线弹性有限元模型进行稳定性分析。 模型了包含741 个单元，669 个节点。 边界条件设置为：主梁与侧拱肋之间的节点为活动铰支座，主拱肋固定在桥台上。

3 设计荷载

本文在桥梁设计中考虑了3 种荷载：（1）恒载；（2）活荷载；（3）风荷载。 所有的静载都以负z 方向施加，交通荷载直接作用于结构上。 为简便起见，假定所施加的交通荷载均匀地分布在桥面上，设计活荷载取33.26 kN/m。

桥梁设计的风荷载根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》确定。 主梁和拱肋受以下3 个风荷载分量，即阻力Fy、升力Fz和俯仰力矩M 分别为：

式中，Cy、Cz及CM为静态气动系数，分别为阻力系数、升力系数和俯仰力矩系数；ρ 为空气密度；B 为拱肋宽度；D 为拱肋的垂直投影面积；VZ为高度Z 处的风速。

式中，V10为10 m 高度的设计风速。

作用在桥面上的风荷载的3 个组成部分如图1 所示。本文研究的主梁静态气动系数分别为Cy=1.347、Cz=0.215、CM=-0.005 5。拱肋的静态气动系数为Cy=1.255、Cz=0.258、CM=1.225。

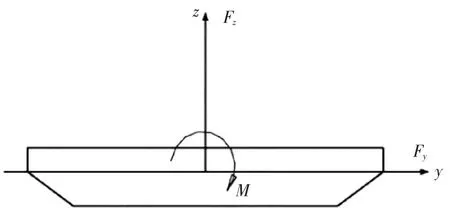
图1 大跨径钢桥三维有限元模型

4 可靠性分析

4.1 极限状态函数

本文在评估钢拱桥可靠性时考虑了基于稳定破坏的极限状态函数。 稳定性极限状态的一般形式可以表示为：

式中，Pcr为根据结构分析估算出的相应的整体挠曲荷载；Pmin为可以用来保证桥梁整体稳定性的最小屈曲载荷。 在稳定性分析中，屈曲载荷一般描述为初始载荷与载荷系数的乘积；因此，式（5）可以表示为：

式中，λcr和λmin分别为整体屈曲载荷系数和最小屈曲载荷系数；P 为初始载荷。

式（6）中，P 的取值不影响极限状态面形状。为了评估桥梁的可靠性， 本研究考虑的极限状态需要指定最小屈曲载荷系数λmin，采用最小屈曲载荷系数4.0。

4.2 可靠性分析方法

在本研究中，极限状态是用有限元法计算的随机变量的隐函数[5]，本研究可采用广义一阶可靠性方法进行分析。 将有限差分法和确定性分析方法相结合，得到极限状态函数的导数。

考虑到目前可用的确定性方法及前文的假设， 本研究采用特征值法来确定桥梁的屈曲载荷系数λcr，假设几何刚度[Kg]与施加的荷载F 成正比，线性增量平衡方程可表示为：

式中，[Ke]为线性弹性刚度矩阵；[Kg]为几何弹性刚度矩阵；{△u}和{△F}分别为增量位移向量和力向量，当位移增加而荷载不增加时，结构就会发生弯曲，此时，{△F}为零。 因此，式（7）表示为：

5 风致失稳可靠性评估

根据对最不利荷载组合的灵敏度分析表明： 静气动系数参数、弹性模量、质量密度、横截面面积、拱肋和主梁的平面内惯性矩对最不利荷载组合下的桥梁可靠性指标有较大影响；表明随机边梁参数对于分析结果是至关重要的。

根据上述结果， 可以得出静气动系数是影响桥梁可靠性最重要的参数。 在本研究中，该参数的散度采用变异系数d 来计算的，分别采用0.4、0.3 和0.2 三个不同的d 值进行计算，计算结果如表2 所示。 从表中可以看出，d 的取值对桥梁可靠性具有显著的影响，d 值越大（参数离散度越大），桥梁的可靠性指标β 越低（桥梁的破坏概率越高）。

表2 最不利荷载作用下不同d 值对钢桥的可靠性影响

在大跨径钢拱桥风致失稳可靠性分析中， 应适当考虑静气动系数的影响。 为了研究风向对桥梁可靠性的影响，本文考虑了两种工况：工况一（不考虑风向）：基本风速V10的平均值为17.86 m/s，变化系数为0.178 m/s；工况二（考虑风向）：基本风速V10的平均值为11.86 m/s，变化系数为0.240 m/s。结果见表3。 不考虑风向的结果与考虑风向的结果基本一致，表明风向对桥梁抗风稳定性破坏的可靠性影响较小。

表3 风向对钢桥风致失稳的可靠性影响

为了研究风荷载的3 个分量对随机钢拱桥结构风致稳定性的影响，本文对最不利荷载作用下的3 个工况进行了分析。工况Ⅰ：只考虑风荷载的阻力；工况Ⅱ：同时考虑风荷载的阻力和升力；工况Ⅲ：考虑风荷载的阻力、升力和俯仰力矩。 除参数V10外，其于风速平均值在17.6～52.8 m/s，风荷载的3 个分量对不同情况下桥梁失效概率的影响如图2 所示。 从图中可以看出， 当V10的均值为17.6 m/s 时，3 种情况下的失效概率差异并不明显，但随着V10平均值的增加，失效概率差异不断增大。 因此，在较大的风荷载或较大的风速下，桥梁的可靠性分析中应考虑风荷载的三分量。 值得注意的是，风荷载三分量对桥梁失效概率的影响在最不利荷载中更明显。

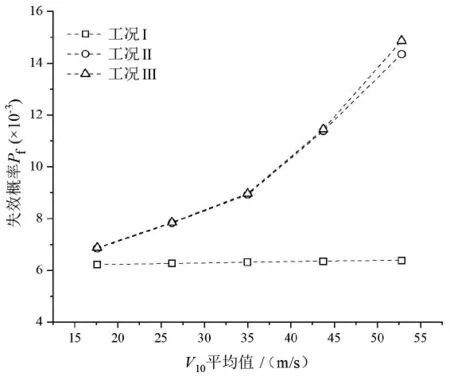
图2 不同工况下钢桥失稳概率与V10 平均值之间的关系

6 结语

本文提出了一种适用于大跨径钢拱桥风致稳定失效的可靠性评估方法，采用特征值法预测了钢桥结构的风致稳定性，对某大跨径钢拱桥抗风稳定性破坏的可靠性进行了评估。 结果表明：

1）该方法可用于评估由不同类型结构元件和材料组成的大跨径结构系统抗风失稳破坏的可靠性；

2）静气动系数是影响钢拱桥抗风失稳可靠性最重要的变量；

3）钢拱桥静气动系数的离散性对其可靠性估算有重要影响。