基于多分类不均衡支持向量机的制造型企业财务管理研究

吴恒铭，张忠良

（杭州电子科技大学管理学院，杭州 310018）

1 引言

在经济全球化的背景下，我国制造业上市公司的规模不断扩大，与此同时，企业面临许多不确定性的微观或宏观因素，企业在财务管理上的挑战随之增加[1]。在我国对制造企业的财务管理研究中，大部分把企业的状况分为两类，即把ST企业定义为存在财务管理问题的样本，非ST 的企业定义为经营正常的样本。但是，这种二分类的处理存在两方面的问题。第一，忽略了企业的其他状况，企业的状况除了经营正常和出现财务问题，还存在进入退市整理期和终止上市等情况，这些状况还可能发生变动，即企业的状况存在着多种变动情况；第二，在实际数据中，由正常经营到ST、由ST 到终止上市、由ST 转为正常经营等这些样本往往存在不平衡的问题，有的变动类型的样本数量会远大于其他样本，而传统的机器学习模型在面对不平衡数据时性能表现不佳[2]。

综上，制造型企业的财务管理问题实际上是一个多分类不均衡的问题，本文用支持向量机（Support Vector Machine，SVM）与哈夫曼树（Huffman Tree，HT）结构结合，将支持向量机扩展为多分类支持向量机模型，并缓和不平衡问题，在此基础上，利用算术优化算法（Arithmetic Optimization Algorithm，AOA）来寻找模型的全局参数，根据模型结果，对制造型企业的财务管理提供相关建议，将本文模型称为AOA-HT-SVM。

2 相关理论

2.1 制造型企业财务管理面临的问题

2.1.1 内部管理问题

管理制度因素，不完善财务控制制度、风险管理制度和授权审批制度可能导致企业运行出现异常；生产决策因素，管理者需要对企业的内外部的生产或采购进行评估，制定适时恰当的决策来管理好企业财务；融资因素，制造企业通常需要融资并投入生产装置和原材料中，然而，市场波动、利率不确定或融资渠道受阻可能影响企业的融资成本[3]。

2.1.2 外部管理问题

自然不可抗力因素，当面临自然灾害时，如地震、洪水、海啸，可能损坏厂房、在制品和成品，造成企业的财产损失；社会因素，企业在特定的文化、社会环境下生产运营，提供的产品或服务应与相应的社会环境适配；政策因素，税收政策、进出口政策、环境法规政策等会导致企业财务波动，例如，贸易政策的改变会使制造企业面临进出口受阻。

2.2 制造型企业财务管理的作用

①控制成本。对于制造型企业，在劳动力成本不断增加、工厂等生产基础设施有限的情况下，通过财务管理，可以帮助企业识别一些低价值、非核心的制造活动，这能够优化生产，降低运营成本。

②合理分配资金。制造业通常需要购买生产设备与工具，有效的财务管理确保企业将资金正确投入日常经营所需的活动中，避免造成资金占用与浪费。

③优化供应链。供应链对制造企业至关重要，财务管理可以对供应链中的各项过程进行分析，例如，运输过程、库存处理过程、采购过程等，通过对这些过程进行分析，寻找可以优化的步骤，从而提高生产效率。

2.3 支持向量机

支持向量机是一种基于统计学习理论的机器学习方法，其主要目标是找到一个最佳分离超平面，使数据空间中两类样本间隔最大化，同时使分类误差最小化[4]。

当模型的数据集是非线性的或数据不能在当前维度空间中分隔时，支持向量机使用核函数将样本从低维空间映射到更高维的特征空间，常用的核函数包括多项式、径向基函数（RBF）和Sigmoid 核函数。

2.4 算术优化算法

受到加减乘除4 种数学运算的启发，Abualigah et al.[5]在2021 年提出了算术优化算法，该算法分为以下3 个步骤：

①初始化。随机生成候选解，每一轮迭代新产生的最优候选解被认为是最优解或近似最优解。

②全局勘探。使用除法（D）和乘法（M）运算符的数学运算被用于可搜索空间的全局探索。

③局部开发。使用减法（S）或加法（A）的数学运算会产生高密度结果。

3 财务管理模型设计

3.1 多分类不均衡支持向量机

哈夫曼树是具有最短加权路径长度的最佳二叉树[6]，基于哈夫曼树的数据分解策略采用分层的二叉树结构处理多分类数据集，每个结点由一个二元SVM 进行决策，其构造过程如下：

①具有m 个类别的数据集，表示为：

ni表示第i 个类的数量。

②根据ni的大小对C（m）进行升序排列，形成一个新的集合：

③选择C（m'）中的前两个最小元素作为左子节点、右子节点，构造一个新的二叉树节点。新节点的值是其左子节点和右子节点的和：

④删除在C（m'）中选择的两个元素，并将新的节点添加到C（m'）：

⑤重复步骤②、③和④，直到集合C（m'）只剩下一个节点元素，HT-SVM 构建完成。

根据上述构建过程，每个二元SVM 处理的两个类的数量会尽可能地接近，即在没对样本数量重采样或改动算法的情况下，直接改善了数据不平衡的问题。

3.2 模型的参数优化

由于SVM 对惩罚参数和核函数的变化很敏感，需要有合适的方法对这些参数寻优[7]。本文使用算法优化算法（AOA）来寻找模型参数，过程如下：

①种群初始化：AOA 随机生成种群，每个个体编码的内容即需要优化的参数，包括惩罚参数、核函数的类型（线性、径向基函数和多项式），以及核函数的参数。

②设置适应度函数：将训练集和测试集比例设置为0.75∶0.25。在对训练集中的样本进行5 次5 折交叉验证之后，根据类的平均准确率来设计适应度函数。

③适应度评估：根据适应度函数对每个个体的适应度进行评估，排序并保存具有最优解的个体。

④迭代优化：根据AOA 更新规则执行解更新。

⑤获取最优参数和模型测试：在迭代完成后得到最优参数，使用最优参数训练并在测试集样本上进行测试。

4 实证分析

4.1 数据获取与预处理

4.1.1 数据获取

本文从CSMAR 数据库选取2013-2022 年间沪深A 股市场中制造业上市公司数据，数据为存在财务管理问题的企业样本，详细情况如表1 所示。

表1 数据类型分布

以上的企业状况代表字母及变动类型划分均来自国泰安数据库，具体含义为：A 为正常上市，B 为ST，D 为*ST，T 为退市整理期，X 为终止上市。AB 为企业的由正常上市转变为ST，AD 为正常上市转变为*ST，以此类推，DT 为*ST 转变为退市整理期。为了样本类型的全面性，进一步选取500 个经营正常的企业样本，即AA 样本，总计样本1 323 个。本文使用T-2 的数据来构建模型，进而对企业T 年的变动状况进行分析。

选择的指标汇总如表2 所示，分别从7 种指标类型中选取了28 个指标。

表2 指标选取汇总

4.1.2 数据预处理

在初步选择的指标中，有的指标可能对企业的状况没有显著影响。因此，有必要删除对企业状况类别无明显影响的变量，降低此类变量对模型能力的干扰。

利用K-S 检验对各个指标进行正态性检验，当指标服从正态分布时，用T 检验来判断样本是否存在显著差异；当指标不服从正态分布时，用K-W 检验进行判断。

从K-S 检验结果来看，所有指标均拒绝了原假设，说明均不服从正态分布。因此，采用K-W 检验非参数检验，根据K-W 的检验结果，固定资产比率、第一大股东持股比例、股权集中指标4（%）3 个指标保留了原假设，说明在各类别中没有显著差异。将其余的拒绝原假设的指标作为最终选择的指标。

4.2 模型测试与结果

为了探究哪一类指标对企业财务状况的效果影响更大，通过剔除该类指标构建新的数据集，将模型效果与保留所有指标的模型效果进行对比，查看该类指标的影响。将剔除发展能力类指标的数据集定义为D1，剔除经营能力为D2，剔除偿债能力为D3，剔除每股指标为D4，剔除盈利能力为D5，剔除比率结构为D6，剔除补充的指标为D7，指标全部保留为D。表3 展示了AOA-HT-SVM 在各个数据和类别上的准确率以及平均准确率。

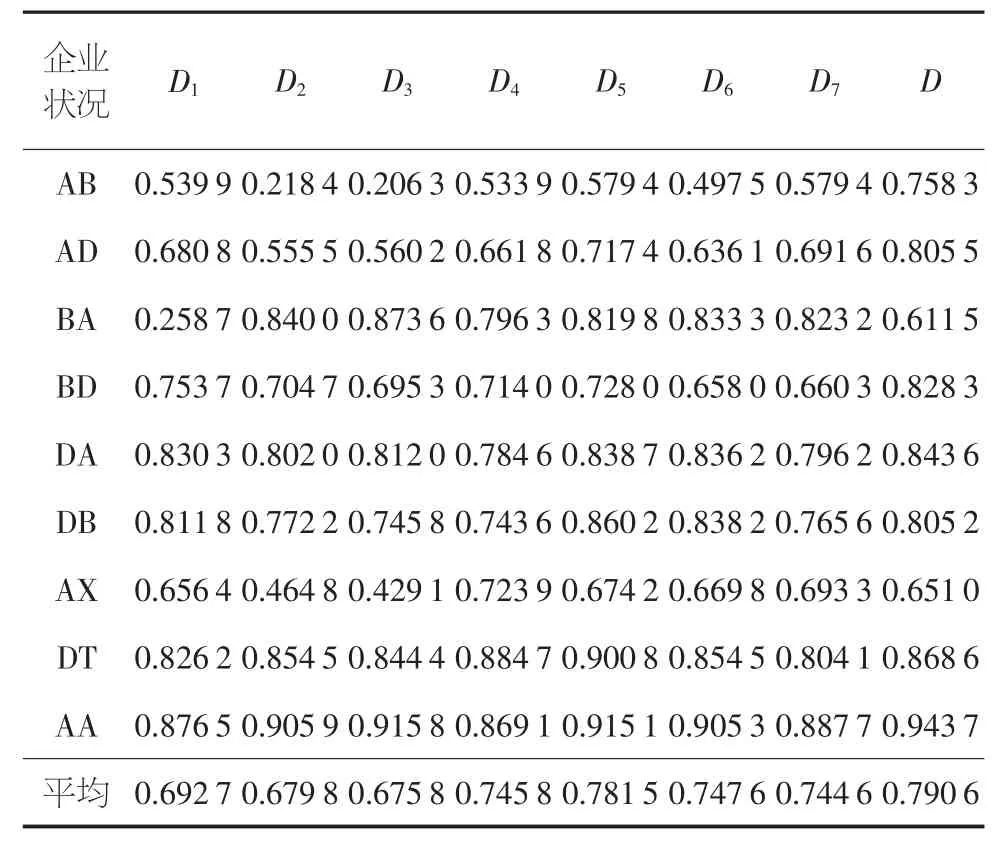
表3 AOA- HT- SVM 在各个数据上的结果

根据表3，从不同数据集的结果来看，D1、D2、D3对企业状况的影响最大。当剔除发展能力、经营能力或偿债能力这3类指标时，平均准确率分别为0.692 7，0.679 8，0.675 8，当保留所有指标时，为0.790 6，模型效果明显提升。说明对于制造型企业，要维持企业在健康稳定状态，应关注其发展能力、经营能力和偿债能力。

4.3 对制造型企业的管理建议

①稳步提升企业的发展能力

制造企业可以通过了解不同市场的需求，推动产品多样化和技术创新，提供符合多个市场需求的产品，以此为企业带来更多的收入。

②优化企业的经营能力

制造企业可以通过产品的整合，降低生产流程的成本和管理的复杂度，推动产品模块化生产，从而提高产品的生产效率和交付水平。

③重视企业的偿债能力

企业在平时应该加强存货管理，避免过高的库存造成资金占用，确保企业有一定的资金用于偿债，同时也应积极主动偿还债务。

5 研究结论与展望

5.1 研究结论

①针对多分类不均衡的制造企业财务管理问题，本文以支持向量机为分类器，首先构建基于哈夫曼树的支持向量机模型，将多分类问题转化为一系列相对平衡的二分类问题，使其能有效地处理企业数据，并使用算术优化算法进行参数寻优。

②使用本文提出的AOA-HT-SVM 模型对制造型企业状况进行研究，实验结果显示，制造型企业的发展能力、经营能力、偿债能力对企业状况的影响较大，公司应注重提升这些能力。

5.2 未来展望

①本研究通过选取财务类指标对制造业公司财务管理进行分析，未来研究可以将非财务指标因素考虑进去，更全面地进行企业状况分析。

②制造业内部不同行业之间存在一定差异性，如果能针对细分制造业行业进行分析，更有助于为企业提供针对性的经营建议。