氧化铝耐火材料制备中热应力有限元分析

栾 雪，赵 莹，陈滨滨，蔡酉铖，程桂石，王孝强，董长青

（华北电力大学 新能源学院，北京 102206）

0 引言

耐火材料广泛应用于钢铁冶炼、水泥、陶瓷、玻璃、电力、有色金属、化学工业等高温行业，是这些工业中的基础支撑材料[1-3]。在苛刻的工作环境中，耐火材料会受到高温气固液物质的共同作用。一方面，熔渣等物质会侵蚀材料表面；另一方面，热应力破坏也是造成耐火材料损伤的主要原因。因此，耐火材料需要良好的抗腐蚀性能和抗高温性能[4-6]。

国内外学者对耐火材料温度场和应力场进行了大量研究。文献[7]研究了二氧化硅耐火材料在不同强度热冲击载荷下的损伤情况，证明了疲劳在实现亚临界裂纹形成和阻止裂纹方面的作用。文献[8]以编制陶瓷基复合材料为对象，研究了与温度相关的损伤行为，预测了各种使用温度下残余应力分布和相应的生产损伤，分析了温度相关的非线性应力–应变行为。文献[9]模拟了熔铸AZS-33#砖铸件冷却过程中的热应力场，研究了铸件的热应力分布情况，分析了可能使熔铸材料产生缺陷的原因。文献[10]研究了支撑板不同厚度和长度下的温度分布和热行为，得到了有利于降低耐火支撑框架应力、延长使用寿命的支撑板最佳尺寸。文献[11]设计了一种具有保温和长寿性能的新型轻质钢包；运用状态分析方法和数值模拟技术，对新型轻量化钢包和传统钢包在典型运行模式下的温度分布进行了比较分析。文献[12]分析了不同气孔尺寸及气孔率下，镁铝尖晶石质耐火材料的温度场和热应力场分布情况变化。

文献[13]使用有限元分析了烧成过程中升、降温速率对大型氧化铬坯体断裂的影响。

目前对于耐火材料的模拟研究主要集中于服役过程中的受力情况分析，而对制备过程中的模拟计算相对较少。

为了进一步发现烧成过程中的相关影响因素，本文将利用ANSYS有限元分析软件，分别模拟氧化铝耐火材料在不同制备条件下的温度场和热应力场，分析模型尺寸、热处理温度、升温速率、降温速率和气孔率因素对裂纹产生的影响。

1 氧化铝砖坯二维模型

1.1 氧化铝砖坯模型

为了简化氧化铝砖坯烧成的模拟过程，采用二维几何模型进行有限元分析。

设置单元类型。在进行建模前，需要选择合适的热分析单元类型。在预处理Preprocessor中，选择单元类型Element Type，将氧化铝砖坯二维模型的单元类型设置为Solid-Quad 4node 55固体。

定义材料属性。选择Material Models，并设置材料的热导率、比热容和密度。

建立物理模型。点击Modeling，选择Create建立矩形Rectangle。

有限元网格划分。在Meshing中设置网格尺寸，将一个连续整体划分为有限个离散单元，结果如图1所示。

图1 氧化铝砖坯二维模型Fig.1 Two-dimensional model of alumina brick blank

氧化铝物性参数如表1所示[14]。

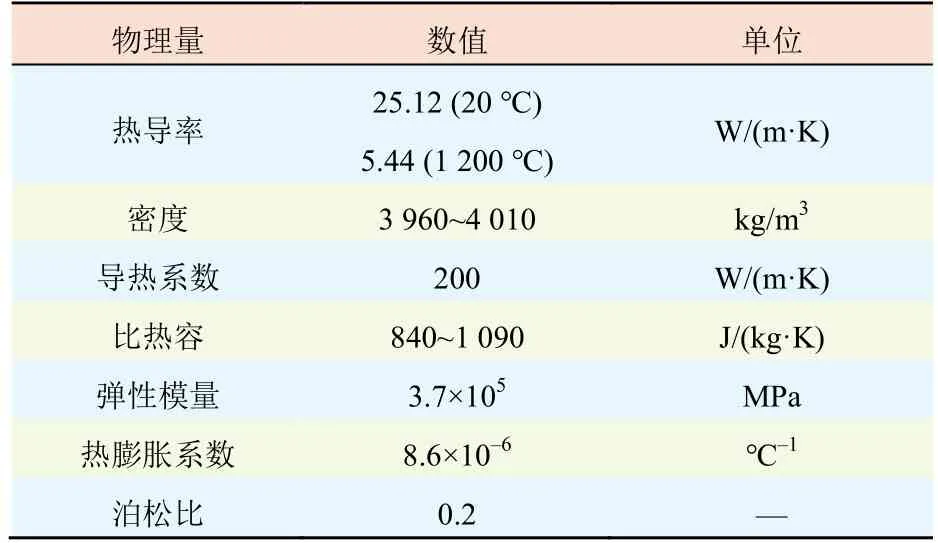
表1 氧化铝物性参数Tab.1 Physical properties of alumina

1.2 边界条件

氧化铝砖坯与高温烟气直接接触，所以可以将氧化铝砖坯表面温度近似地看作与高温烟气一样，满足第一类边界条件[15]。

式中：Γ为物体边界；t(x,y)为边界温度。

在氧化铝砖烧成的过程中，表面与流动的高温气体的热边界条件是第三类边界条件[15]。

式中：h为表面传热系数；Tf为流体的温度。

氧化铝砖在烧成过程中不受外力的作用，所以计算过程为瞬态热交换过程。氧化铝砖内部无热源。氧化铝砖的热应力属于弹性力学的范畴，满足热弹性平衡方程[16]：

式中：、、分别为x、y、z方向的法向应力；为沿着z方向的在xy面上的剪应力，为沿着y方向的在xz面上的剪应力，为沿x方向在yz面上的剪应力；ε为热应力系数；T为瞬态温度。

在窑炉内的烧成过程中，氧化铝砖坯经历的传热形式主要是热对流和热辐射。热边界主要为氧化铝砖的各个表面，其换热系数设置为200 W/(m·K)。

采用瞬态热分析计算温度场。在进行结构分析时，热应力场的模拟基于温度场的计算结果。

2 结果与讨论

2.1 不同尺寸下模型热应力值

实验条件设置：砖坯尺寸分别为70 mm×15 mm、70 mm×20 mm、70 mm×25 mm；温度从室温20 ℃升温到1 600 ℃。升温速率如表2所示。

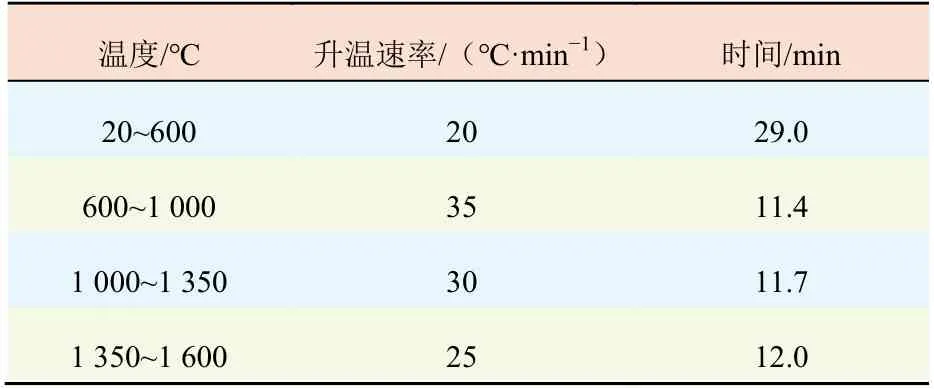
表2 氧化铝砖坯从20 ℃升温到1 600 ℃各阶段升温速率Tab.2 The heating rate of alumina bricks at each stage from 20 ℃ to 1 600 ℃

计算砖坯温度场和热应力场。

图2为70 mm×15 mm的砖坯升温到1 600 ℃时的热应力分布云图。由图可知，最大热应力值分布在坯体中心，表现为拉应力。热应力值由中心向表面递减。最小热应力值分布在上表面，表现为压应力。

图2 温度为1 600 ℃时热应力分布云图Fig.2 Thermal stress distribution at 1 600 °C

图3示出了70 mm×15 mm、70 mm×20 mm、70 mm×25 mm这3种尺寸的砖坯升温过程中最大热应力值变化趋势。

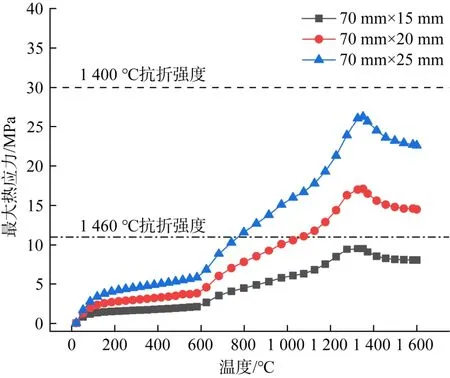
图3 不同尺寸氧化铝砖坯的最大热应力变化曲线Fig.3 Maximum thermal stress curve of alumina brick blank with different sizes

从图中可以看出，随着温度的升高，各种尺寸对应的最大热应力值呈现先增大后减小的趋势，峰值出现在1 200～1 400 ℃温度区间内。同一温度下，最大热应力值随着砖坯尺寸的增大而升高。氧化铝耐火材料在1 400 ℃和1 460 ℃时的抗折强度分别为30 MPa和11 MPa[17]。当窑炉内温度升高到1 400 ℃时，3种尺寸砖坯对应的最大热应力值都没有超过30 MPa，裂纹产生的概率小。当温度升高到1 460 ℃时，只有尺寸为70 mm×15 mm的砖坯对应的最大热应力值并未超过氧化铝材料的抗折强度。由此可知，砖坯尺寸越大，其最大热应力值也就越大，产生裂纹的概率越大。因此，应适当地缩小氧化铝砖坯的尺寸来降低裂纹产生的风险。

2.2 不同热处理温度下热应力值

实验条件设置：砖坯尺寸为70 mm×15 mm。升温速率设定如表2。分别计算热处理温度为1 600 ℃、1 650 ℃、1 700 ℃、1 750 ℃以及1 800 ℃时的热应力场。

图4示出了不同热处理温度下，最大热应力值随温度的变化趋势。

图4 不同热处理温度下氧化铝砖坯的最大热应力值Fig.4 Maximum thermal stress of alumina brick blank at different heat treatment temperatures

由图可知，当窑炉内烧成温度从室温分别上升到1 600 ℃、1 650 ℃、1 700 ℃、1 750 ℃和1 800 ℃时，氧化铝砖坯内部对应的最大热应力值分别为8.03 MPa、8.02 MPa、5.48 MPa、4.91 MPa、4.80 MPa。从图3可以看到，在200～600 ℃区间内，最大热应力值变化缓慢，600～1 200 ℃区间内，最大热应力变化明显。从图4可以看到，温度达到1 600 ℃之后，继续升温时，最大热应力值反而呈现下降的趋势。这是由于，当温度达到1 600 ℃之后，再继续升温时，耐火材料内部与表面的温度差减小，使得对应的最大热应力值下降。

2.3 不同升温速率下热应力值

实验条件设置：砖坯尺寸设置为70 mm×15 mm，从室温20 ℃升温到1 600 ℃。

分别模拟不同升温速率下的温度场和热应力场。

由资料文献[14]可知，在耐火材料烧成过程中，在1 000～1 350 ℃温度范围内，热应力受温度影响变化敏感。因此，选择其他温度区间升温速率保持不变，将1 000～1 350 ℃温度区间的升温速率分别设置为20 ℃/min、25 ℃/min、30 ℃/min、35 ℃/min以及40 ℃/min，具体如表3所示。

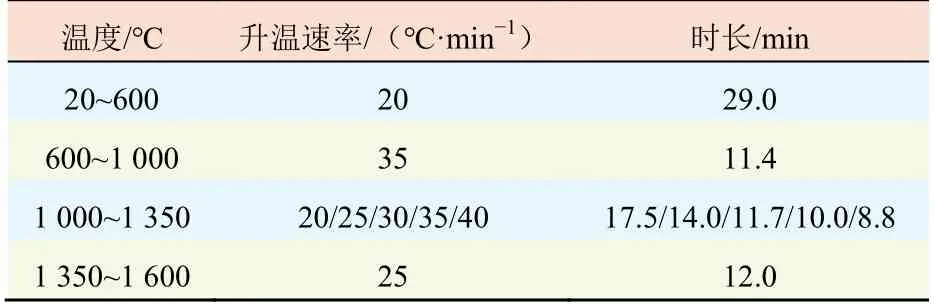
表3 氧化铝砖坯不同温度区间的升温速率设置Tab.3 Setting of heating rates for alumina brick blank in different temperature ranges

图5示出了不同升温速率下最大热应力值的变化趋势。

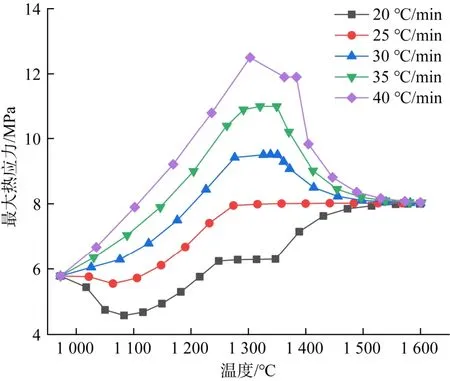
图5 不同升温速率下氧化铝砖坯的最大热应力变化曲线Fig.5 Maximum thermal stress curves of alumina brick blank under different heating rates

由图5可知：

1）在1 000～1 600 ℃温度区间内，随着温度的升高，30 ℃/min、35 ℃/min以及40 ℃/min升温速率下的最大热应力值先升高并在1 200～1 400 ℃温度区间内达到峰值，然后再下降。

2）在20 ℃/min和25 ℃/min升温速率条件下，最大热应力则是呈现出先下降、再升高，最后达到最大值的趋势。

3）在不同升温速率条件下，窑炉内环境温度达到1 600 ℃时材料内部的最大热应力值趋于一致。

4）升温速率越快，最大热应力值随着温度变化越明显。考虑到此条件下坯体产生裂纹的可能性大，因此应适当降低升温速率以避免裂纹产生。

2.4 不同降温速率下热应力值

实验条件设置：砖坯尺寸为70 mm×15 mm。降温速率为10 ℃/min。砖坯温度从1 600 ℃降温到20 ℃。

图6为在该实验条件下获得的砖坯热应力分布云图。由图可知，最小热应力值表现为压应力，分布在砖坯中心；最大热应力值表现为拉应力，主要分布在砖坯上表面中心部位。该模拟结果与文献[13]研究的氧化铬坯体在降温过程中的热应力分布相似。

图6 以10 ℃/min速率降温到室温时砖坯热应力分布Fig.6 Thermal stress distribution of brick blank when cooling to room temperature at a rate of 10 ℃/min

在冷却过程中，表面温度下降较快，收缩较多，因此表面受到拉应力作用；而材料内部温度下降缓慢，受力情况相反，受到压应力作用。

图7示出了不同降温速率下最大热应力值变化趋势。由图可知，在1 400～1 600 ℃温度区间内，随着温度的降低，最大热应力值快速增大；1 200～1 400 ℃区间内，热应力达到最大值，说明此温度段为砖坯发生开裂或断裂的危险阶段，故应该严格控制此区间内砖坯的降温速率；在温度达到1 200 ℃之后，最大热应力值缓慢下降，并且冷却速率越小，对应的最大热应力值也相对越小。

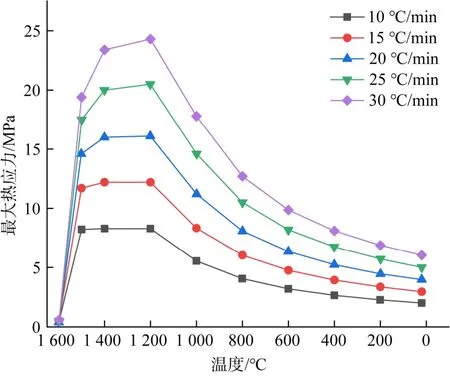
图7 不同降温速率下最大热应力变化曲线Fig.7 Maximum thermal stress curves at different cooling rates

2.5 不同气孔率的热应力值

实验条件设置：砖坯尺寸为18 mm×6 mm，气孔半径为0.1 mm，升温速率如表2所示。

在上述实验条件下开展氧化铝砖坯温度场和热应力场的模拟。

考虑到最大热应力的峰值出现在1 200～1 600 ℃温度区间内，因此计算气孔率分别为5%、7%和10%时，砖坯在1 200 ℃、1 300 ℃、1 400 ℃和1 500 ℃下的最大热应力值。

图8示出了不同气孔率设置值下氧化铝砖坯的最大热应力值变化趋势。

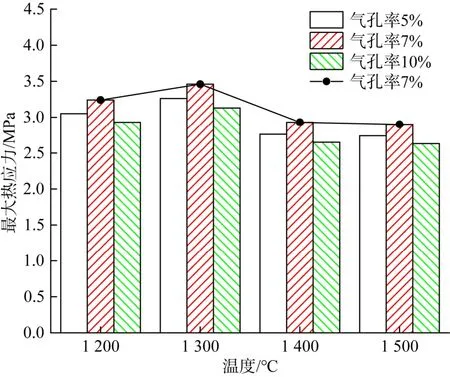
图8 不同气孔率下最大热应力变化趋势Fig.8 Trend of maximum thermal stress at different porosities

由图可知，3种气孔率砖坯的最大热应力在各温度下的变化趋势一致。图中折线为气孔率为7%砖坯的最大热应力值变化趋势。曲线中温度值为1 300 ℃时热应力值最大。在同一温度下，气孔率为10%的砖坯对应的最大热应力值最小。因此可以认为，相比之下，砖坯气孔率达到10%这一条件有利于避免裂纹产生。

3 结论

仿真结果表明：

1）升温过程中，最大热应力分布在砖坯中心，由内向外递减。缩小氧化铝砖坯的尺寸有利于避免裂纹产生。

2）最大热应力的峰值出现在1 200～1 600 ℃区间内。缓慢的升温速率及降温速率有利于减少烧成过程中裂纹的产生。

3）砖坯气孔率对最大热应力有一定影响。气孔率10%的砖坯比5%和7%砖坯的最大热应力值小。