基于CNN-SVM的特高压三端混合直流线路故障区域识别方法

周前华，陈仕龙，邓 健，毕贵红，魏荣智

（昆明理工大学 电力工程学院，云南 昆明 650500）

0 引言

目前，基于电网换相换流器(Line commutated converter，LCC)的高压直流输电系统在我国直流输电工程中得到广泛应用[1-3]。然而，这种高压直流输电系统存在逆变侧换相失败的风险。基于电压源型换流器(Voltage source converter，VSC)的高压直流输电系统能够提供动态无功支撑，但其经济成本较高且运行损耗较大。为了充分发挥两者的优点，多端混合直流输电系统应运而生。在多端混合直流输电系统中，整流侧采用LCC换流站，逆变侧采用VSC换流站[4]。由于受端采用了模块化多电平换流器（Modular multilevel converter，MMC），当直流线路发生故障时，其故障电流会在几毫秒内飙升到额定电流的数十倍，这给继电保护带来了巨大的挑战。

由于需要进行远距离大容量功率传输，在多端混合直流输电工程的实际应用中，使用直流架空线路是必不可少的；但是，这种远距离的直流架空线路故障的概率很高[5]。另外，在存在T区的直流系统中，当T区汇流母线发生直流线路故障时，保护装置捕捉到故障信息的能力就会降低[6]。

文献[7]以LCC-MMC混合双极直流输电系统为背景，研究了该系统故障暂态电流行波的突变特征，通过分析整流侧和逆变侧在不同故障情况下暂态电流行波变化的方向差异，来判断故障发生的区域，实现了对区内外故障的识别。

文献[8]通过对T区传递函数的推导与分析，发现换流器的并联接入会减少故障电流行波的中低频分量，并在此基础上提出了一种基于T区两侧暂态电流中低频能量差异的故障方向判别原理。

文献[9]分析了不同位置发生故障时换流器动作前的暂态电流故障分量的极性，通过计算故障后T区汇流母线3个端口的暂态电流故障分量的相关系数来实现故障区域的准确判别。该方法具有速动性较好及耐受大过渡电阻等优点。

以上文献所提出的保护方案虽然克服了T区这一特殊结构的难点，但是都需要面对复杂的阈值整定和计算环节。

基于人工智能算法的保护方案具有自适应性和自学能力，在应用时能够避免传统方法中需要手动设置阈值的问题，在直流输电系统的故障识别领域具有广泛的应用前景。

文献[10]提出基于堆叠自编码器(Stacked auto-encoder)的故障区域识别方法，选取故障条件下电压反行波的线模量与零模量作为输入数据样本进行故障识别。

文献[11]选取不同位置的故障电压、电流数据作为输入量，在对CNN的网络结构和训练优化的基础上完成了故障区域判断。

文献[12]提出了一种基于CNN-SVM的高压输电线路故障分段识别方法。该方法对高压输电线路故障识别率较高。

以上文献所提保护方案均以柔性直流电网作为对象，但是混合直流电网存在T区这一特殊结构，而T区结构的系统故障又有其特有特性。

基于含T区线路故障的特殊性，本文首先分析昆北LCC侧、柳北MMC1的T区边界、龙门MMC2侧的直流线路边界的频率特性，从而得出暂态信号中的高频分量在LCC侧直流边界、MMC1侧T区、MCC2侧直流边界的幅值衰减情况；然后，通过经验小波变换提取故障特征，将其作为CNN-SVM的输入量，将故障区域作为输出量，从而构建出CNN-SVM故障区域识别模型；最后，通过仿真验证测试模型对不同故障区域故障的识别准确率、耐受过渡电阻能力。

1 特高压三端混合直流输电系统

昆柳龙混合直流输电系统为典型的特高压三端混合直流输电系统。系统送端是昆北站，容量为8 GW；受端分别为广东龙门、广西柳州，容量分别为5 GW、3 GW；线路总长约1 450.4 km。昆柳段线路为908.4 km，柳龙段线路为542.0 km。

本文以±800 kV昆柳龙混合三端直流输电工程作为原型进行分析。图1为±800 kV昆柳龙特高压三端混合直流输电系统仿真模型。

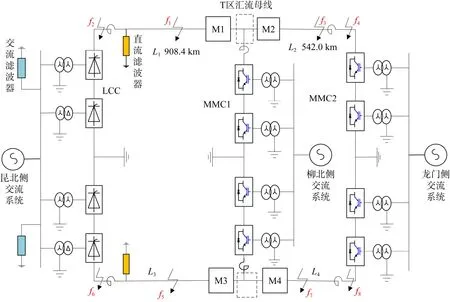
图1 ±800 kV特高压三端混合直流输电仿真模型Fig.1 Simulation model of ±800 kV UHV three-terminal hybrid HVDC transmission

图中，送端昆北换流站和受端龙门换流站分别通过直流线路L1以及直流线路L2连接至受端柳北换流站内的汇流母线上，构成T区。M1、M2代表安装在正极T区左右两侧的保护装置；M3、M4代表安装在负极T区左右两侧的保护装置。

2 直流线路边界频率特性分析

为了能够避免其他不必要因素影响，对由测量点M得到的原始数据实行处理，得到一模分量和零模分量，如式（1）所示。

式中：u0、u1分别为M处的零模电压和一模电压；uP、uN分别为M处的正极电压与负极电压；i0、i1分别为M处零模电流与一模电流；iP、iN分别为M处的正极电流与负极电流。

由于零模分量在传播时衰减程度比一模分量严重，因此本文只对一模电气量进行分析。

2.1 LCC侧直流边界频率特性分析

LCC侧线路首端的2组三调谐直流滤波器与平波电抗器构成了整流侧线路的物理边界，如图2所示。

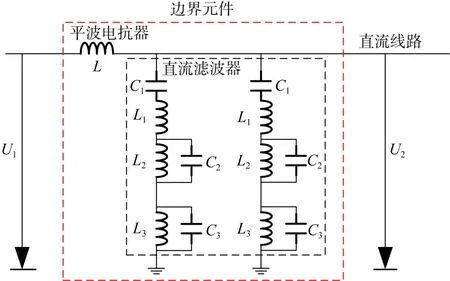
图2 LCC侧直流线路边界Fig.2 DC line boundary on the LCC side

利用文献[13]方法对图2 LCC侧直流线路边界中的平波电抗器和直流滤波器进行分析，可以发现出暂态信号中高频分量在LCC侧边界的作用下会有明显的幅值衰减。

2.2 MMC1侧T区频率特性分析

文献[8]对含T区这一特殊结构的模型进行了剖析。本文利用该模型对所含T区边界传递函数幅频特性进行分析。

由于发生故障时，线路L1和线路L2的T区等效电路的故障特征类似，故以T区左侧线路L1故障为例来分析，其故障分量的等效电路如图3所示。

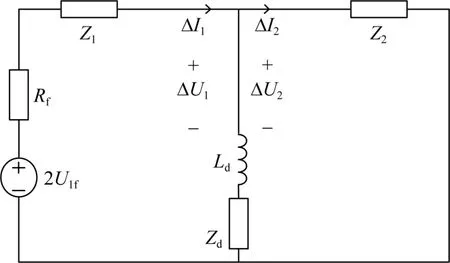
图3 直流线路L1故障分量等效电路Fig.3 L1 fault component equivalent circuit of DC line

图3中，U1f表示故障点附加一模电压源；Rf表示过渡电阻；Z1和Z2分别表示线路L1和线路L2的一模波阻抗；Ld表示平波电抗器；ΔI1、ΔI2、ΔU1、ΔU2分别表示线路L1和线路L2故障暂态信号的线模分量；Zd表示MMC1的等值阻抗。

利用文献[13]方法进行分析，发现暂态信号中的中低频段在MCC1侧T区边界的作用下会有一定的幅值衰减。

2.3 MCC2侧直流边界频率特性分析

对于MCC2侧，线路L2末端的平波电抗器可以作为直流边界元件。考虑到架空线路的对地电容，故利用一段架空线路的对地电容和线路L2末端的平波电抗器来构成MMC2侧直流输电线路的物理边界，其结构如图4所示。

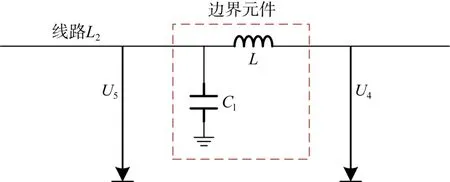
图4 MCC2侧直流线路边界Fig.4 DC line boundary on the MCC2 side

结合图4中的平波电抗器和对地电容的实际参数，通过文献[13]方法进行分析可以得出：暂态信号中的高频分量在MCC2侧边界的作用下会有明显的幅值衰减。

3 基于CNN-SVM的故障区域识别

3.1 保护启动元件

当直流线路发生故障时，测量装置所检测到的电流数据会发生较大变化，故可以利用暂态电流突变量来构成保护启动判据。

为了保证采集到的数据在时域上的同步性，设置启动判据均采用测量点截取窗口的起始数据。

考虑实际正常运行时，线路电流会存在波动，故预留10%的裕度。启动判据[11]为：

式中：IM为测量装置检测到的单极电流值；为电流变化量；In为正常运行时的额定电流。

3.2 故障特征提取方法

本文选取经验小波变换提取故障特征是因为该方法基于信号特征自动地将信号分解为一组有限数目的IMF分量，不需要选取小波基函数，在处理非线性和非平稳信号方面表现尤为出色[14,15]。

3.3 T区故障识别

分析T区频率特性可知，在L1发生故障的情况下，T区对中低频故障暂态信号会有衰减作用。T区左侧的保护装置M1所检测到的暂态电流一模信号中的中低频分量远大于T区右侧的保护装置M2。因此，可以利用T区两侧保护装置M1、M2所检测到的暂态电流一模信号中低频分量的波形差异来区分故障发生在线路L1还是线路L2。

在仿真模型中验证T区对一模电流中低频分量的衰减作用。设置模型采样频率为20 kHz；故障发生地点为线路L1中点处（距保护装置M1左侧454.2 km）及线路L2中点处（距保护装置M2右侧271 km）；采样数据时间窗为4 ms；过渡电阻分别为0.01 Ω、50 Ω、100 Ω、150 Ω、200 Ω、250 Ω、300 Ω。

保护装置M1、M2采集到的一模电流中低频分量波形如图5、图6所示。

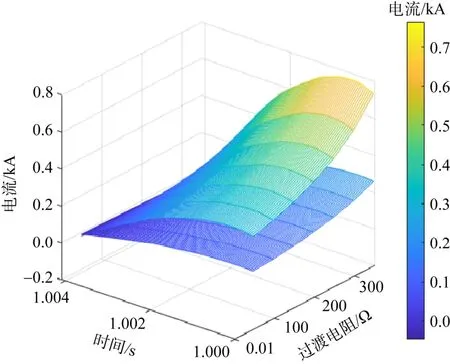
图5 线路L1故障，M1、M2处一模电流中低频分量波形Fig.5 Waveform of low-frequency component of one-mode current at M1 and M2 of line L1 fault

图6 线路L2故障，M1、M2处一模电流中低频分量波形Fig.6 Waveform of low-frequency component of one-mode current at M1 and M2 of line L2 fault

由图5知，在T区左侧线路L1发生故障时，保护装置M1所检测到的一模电流中低频分量的波形与保护装置M2所检测到的一模电流中低频分量的波形均呈现下降趋势；但是，保护装置M1中的波形的变化趋势明显区别于保护装置M2中的波形的变化趋势，且保护装置M1的波形一直位于保护装置M2的波形上方。由此可以得出：M1一模电流中低频分量的幅值一直大于M2一模电流中低频分量的幅值，并且随着过渡电阻的不断增大，二者之间的趋势愈加明显。该结果符合T区幅频特性的分析结果。

由图6知，在T区右侧线路L2发生故障时，保护装置M1所检测到的一模电流中低频分量的波形与保护装置M2所检测到的一模电流中低频分量的波形均呈现上升趋势；但是，保护装置M1中的波形变化趋势明显区别于保护装置M2中的波形变化趋势，保护装置M1的波形一直位于保护装置M2的波形上方。由此可以得出：M1一模电流中低频分量的幅值一直小于M2一模电流中低频分量的幅值，并且随着过渡电阻的不断增大，二者之间的趋势愈加明显。该结果符合T区幅频特性的分析结果。

综上可得，当T区外L1、L2线路发生故障时，可用由所对应的保护装置得到的一模电流中低频分量的波形特征差异来判断故障发生在T区外L1线路还是L2线路。

3.4 故障识别

LCC侧边界、MMC2侧边界都会对暂态电压高频分量信号强度进行弱化。在L1发生故障的情况下，保护装置M1所检测到的一模电压高频分量会远大于故障发生在L1区外时。当区内线路L2发生故障时，保护装置M2所检测到的一模电压高频分量会远大于故障发生在L2区外时。因此，可以根据对应线路上保护装置所检测到的一模电压高频分量的波形特征来判断故障发生在线路区内还是线路区外。

在仿真模型中验证LCC侧边界对一模电压高频分量的衰减作用。设置模型采样频率为20 kHz；采样数据时间窗为4 ms；故障发生地点距离保护装置M1分别为100 km、500 km、800 km；故障类型为金属性接地。

保护装置M1采集到的一模电压高频分量波形如图7所示。

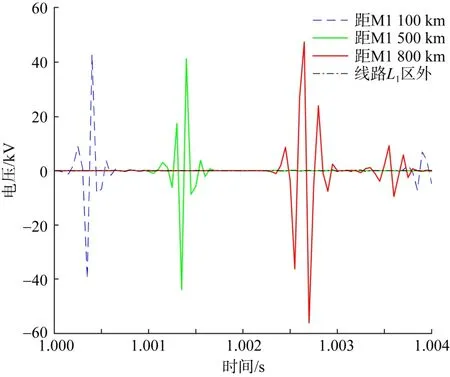
图7 线路L1不同位置故障时M1处一模电压高频分量波形Fig.7 Waveform of high-frequency component of one-mode voltage at M1 fault at different positions of line L1

由图7知，当线路L1区内发生故障时，对于不同位置发生故障，保护装置M1所检测到的暂态电压高频分量的波形突变量大，变化趋势比较明显。当线路L1区外发生故障时，保护装置M1所检测到的暂态电压高频分量的波形比较平坦，趋于一条直线，无明显变化趋势。

在仿真模型中验证MMC2侧边界对一模电压高频分量的衰减作用。设置模型采样频率为20 kHz；采样数据时间窗为4 ms；故障发生地点与保护装置M2的距离长度分别为100 km、400 km、800 km和线路区外。

保护装置M2采集到的一模电压波形如图8所示。

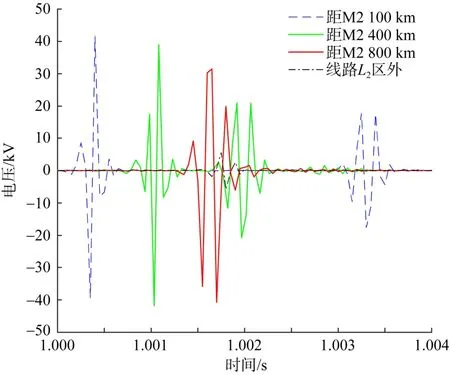
图8 线路L2不同位置故障时M2处一模电压高频分量波形Fig.8 Waveform of the high-frequency component of the one-mode voltage at M2 fault at different positions of line L2

由图8知，当线路L2区内发生故障时，对于不同位置发生故障，保护装置M2所检测到的一模电压高频分量的波形突变量大，变化趋势比较明显。当线路L2区外发生故障时，保护装置M2所检测到的一模电压高频分量的波形比较平坦，趋于一条直线，无明显变化趋势。

综上可得，保护装置M1所检测到的一模电压高频分量波形可以用来区分线路L1的区内外故障；保护装置M2所检测到的一模电压高频分量波形可以用来区分线路L2的区内外故障。因此，可以据M1、M2保护装置上所检测到的一模电压高频分量波形来对故障区域进行判别。

3.5 故障选极

故障线路的电压和电流在直流系统里相比于额定值会有较大的跌落；对于非故障线路，由于受电磁耦合的影响，其电压和电流也会受到波动[16]。为此，对故障后4 ms数据窗内的功率数据进行积分，以提高数据的精确性，达到提高故障区域识别的可靠性的目的。其次，利用保护装置M1、M3上的功率数据来构造故障选极元件，表达式为：

式中：为保护装置M1上的正极功率数据；为保护装置M3上的负极功率数据；k为4 ms内采样点的个数。

当正极线路发生故障时，保护装置M1上k个正极功率数据之和会大于保护装置M3上k个负极功率数据之和，S的值就会大于1；当负极线路发生故障时，保护装置M1上k个正极功率数据之和会小于保护装置M3上k个负极功率数据之和，S的值就会小于1。

3.6 CNN-SVM故障区域识别原理

CNN是一种以卷积层、池化层为基础的具有权值共享等特性的前馈深度学习网络，具有良好的非线性运算能力和特征提取能力[10]；但是针对非线性问题，CNN网络输出层的Softmax分类器分类效果不好，可能使模型可迁移性不足。SVM在处理非线性分类时表现良好。故将这2种技术结合起来，用SVM来代替CNN网络中的Softmax分类器。将CNN提取的初步特征输入到SVM中能够更好地挖掘数据中更深层次的特征，充分发现数据样本之间的相互关系，大幅度提高模型的识别准确率。

本文构建的CNN-SVM结构图如图9所示。图中网络结构主要包括1个输入层、3个CNN层，1个全连接层，1个SVM层，1个输出层。

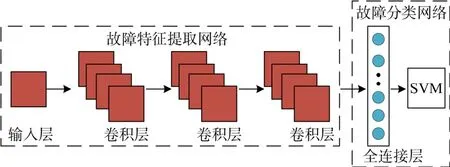
图9 CNN-SVM网络结构Fig.9 CNN-SVM network structure

考虑到输入量的数值差异较大，为了避免数据量纲对网络的训练造成影响，先将输入数据进行Min-Max归一化处理。CNN层的作用是对输入量进行特征分块提取。为了将卷积层所提取到的特征量进行抽象合并，采用全连接层将卷积层所提取到的分布式特征映射到样本标签特征向量。

高斯核函数的作用是衡量样本和样本之间的“相似度”，在一个刻画“相似度”的空间中让同类样本更好地聚在一起，进而使非线性的特征量线性可分，其优点在于：可直接使用映射后的新样本点的点乘计算公式，无需具体计算原始样本点映射的新的无穷维度的样本点，且样本量少、分类精度高，从而使SVM支持向量机能够避免数据分类上的障碍。

在MATLAB平台上搭建CNN-SVM网络模型的各层结构；采用Relu作为激活函数，卷积核大小设置为3×3；初始学习率采用0.001；设置最大迭代次数为4 000；采用Adam优化器对模型参数进行优化，优化算法与误差函数分别为Adam和多分类交叉熵函数，最后使用最大池化进一步提取特征；SVM模块中惩罚因子设置为100，核函数类型设置为径向基函数（高斯），核函数的参数系数为0.01。

故障方向识别。利用T区左右两侧保护装置所测得的一模电流中低频分量的波形特征差异来判断故障发生在T区左侧线路L1还是T区右侧线路L2。

故障线路区内外识别。利用T区左右两侧保护装置所测得的一模电压高频分量的波形特征差异来判断故障发生在线路区内还是线路区外。

故障选极。利用正负极功率的积分比值差异。将上述故障特征差异作为CNN-SVM特征输入量，实现直流线路故障区域识别。将T区两侧保护装置得到的一模电流中低频分量数据、，一模电压高频分量数据、以及正负极功率积分值的比值S作为CNN-SVM的5个输入变量。CNN-SVM每1个输出存在8个值，每个值分别对应故障发生在f1—f8区域的概率。例如，当故障发生在f1区域时，期望的输出为向量（1,0,0,0,0,0,0,0）。故障发生在f2—f8区域时的期望输出向量依次类推。

基于CNN-SVM的故障区域识别流程如图10所示。

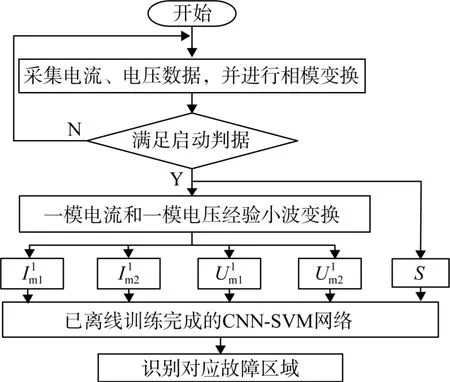
图10 基于CNN-SVM的故障区域识别流程Fig.10 Fault area identification process based on CNN-SVM

4 CNN-SVM训练及测试结果

4.1 CNN-SVM训练

CNN-SVM网络参数设置完成以后，在上述仿真模型上进行故障仿真。

故障类型为单极接地故障。仿真数据共252组。具体训练数据如表1所示。表1中实验数据的采样频率为20 kHz。故障发生时间为1 s。数据窗截取长度为4 ms。过渡电阻变化步长为50 Ω。

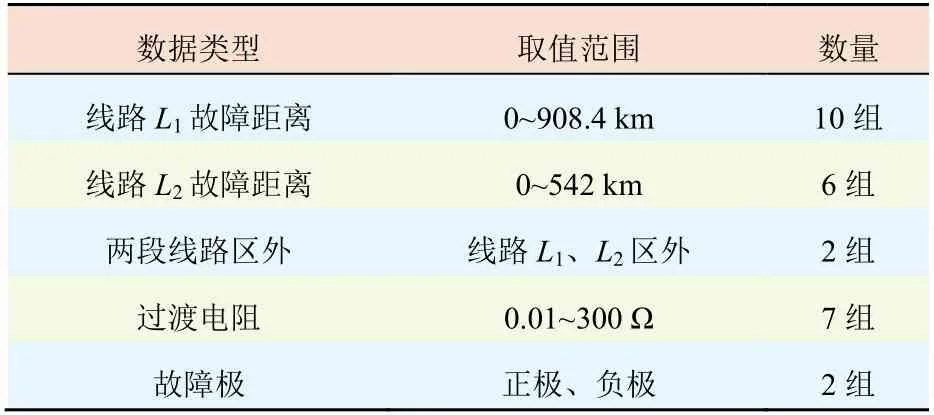
表1 训练数据Tab.1 Training data

训练结果损失值和预测精度曲线如图11、图12所示。

图11 损失值曲线Fig.11 Loss-value curve

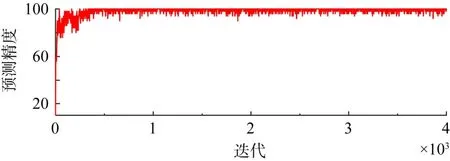
图12 预测精度百分量曲线Fig.12 Prediction accuracy percentage curve

4.2 CNN-SVM测试

利用训练完成后的CNN-SVM网络进行故障区域识别。

直流线路出现位置相异故障。在所得数据达到CNN-SVM训练精度要求条件下，对4个保护装置所捕捉到的故障特征进行提取，并且使用CNN-SVM对其进行训练，最终根据网络输出的编码来判断故障发生的位置。

为了评估CNN-SVM网络在故障识别方面的泛化性能，进行24组模拟实际故障判别情景的单一新测试。这些测试样本不同于训练样本的故障距离和过渡电阻。测试结果如表2所示。

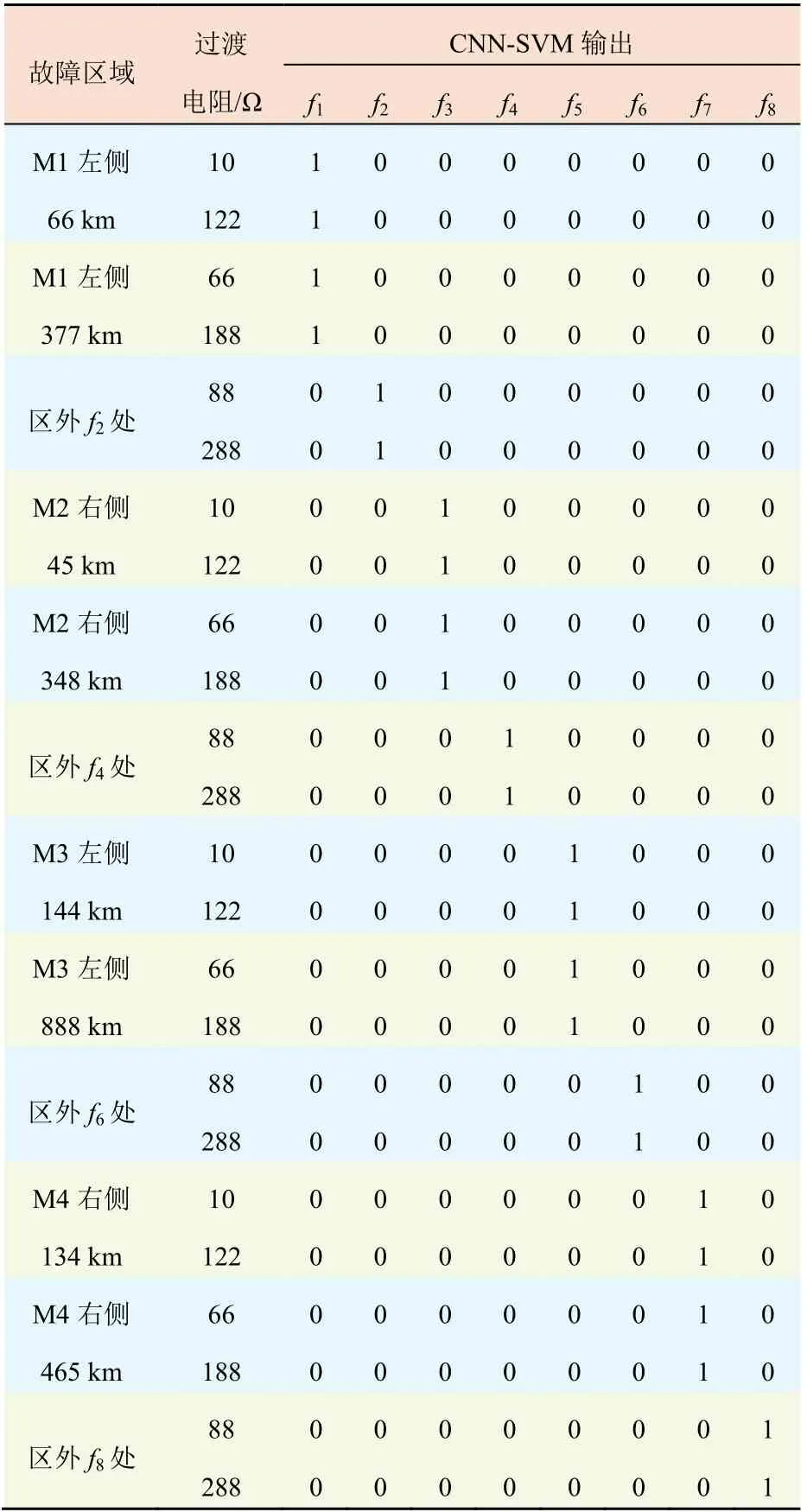
表2 CNN-SVM测试结果Tab.2 Test results of CNN-SVM

由表2可知，即使采用不同于训练样本的数据来测试，经过训练的CNN-SVM网络仍然能够准确识别对应故障区域。

4.3 抗噪声能力验证

为模拟现实噪声信号对测量造成的干扰，在由模型仿真得到的测量点原始电流、电压数据中添加30 dB的白噪声。将添加了30 dB白噪声的原始数据进行数据处理，然后使用训练完成的CNN-SVM对其进行测试。测试结果如表3所示。

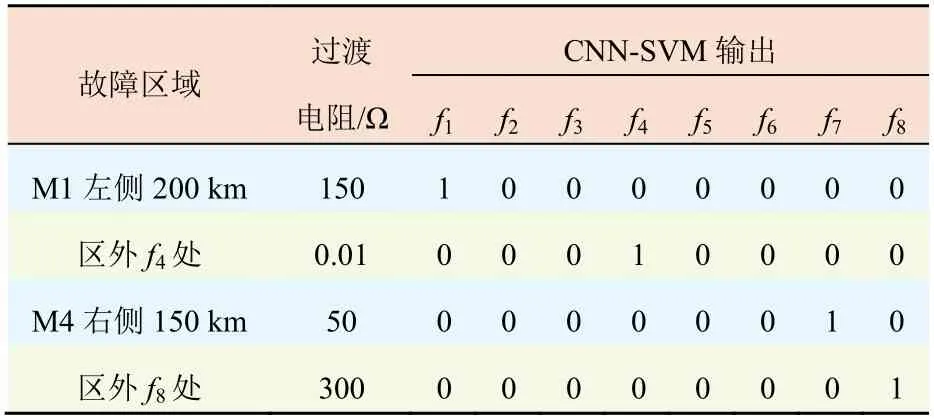
表3 在噪声干扰下CNN-SVM测试结果Tab.3 Test results of CNN-SVM under the noise interference

由表3的测试结果可知，在30 dB噪声干扰下，本文所提出的故障检测方案仍然能够准确识别故障区域，模型具有一定的抗噪能力。

5 结论

针对特高压三端混合直流系统中的直流电网系统，本文提出基于CNN-SVM的特高压三端混合直流线路故障区域识别方法。通过仿真实验，得到以下主要结论。

1）LCC侧、MMC2侧线路边界对暂态电压高频分量存在明显的衰减作用；T区边界对暂态电流的中低频分量存在一定的衰减作用。

2）采用CNN-SVM网络对时序数据进行学习，将CNN网络特征提取能力强的优点与SVM网络分类能力准确的优点相结合，使模型避免了传统保护的人工整定阈值问题，且该方案有耐受300 Ω过渡电阻能力和抗30 dB噪声干扰能力。