Steiner树优化问题的算法研究综述

王军霞，王晓峰，2，彭庆媛，华盈盈，宋家欢

1.北方民族大学计算机科学与工程学院，银川 750021

2.北方民族大学图形图像智能处理国家民委重点实验室，银川 750021

Steiner树问题是一个经典的组合优化问题，在计算机网络布局、无线通信、生物网络分析，以及对给定的一组种子基因或蛋白质进行子网络的识别等领域都有重要的应用[1-2]。最短网络问题是求解最小生成树问题的基础，且最小Steiner树问题（minimum Steiner tree problem，MSTP）与最小生成树问题之间有许多相似之处[3]，最小生成树是在给定的顶点集和边中寻找最短网络使得所有的点连通。MSTP 是使得指定的顶点集合中的所有点连通，且边的权值总和最小的生成树。换句话说，最小生成树是MSTP 的一种特殊情况，因此用于解决MSTP 的启发式算法可以通过延伸和推广最短路径算法和最小生成树算法的思想而得到。STP 是图论中研究较多的组合优化问题[4]，目标是在给定的无向图中找到一棵最小的子图（即Steiner树），使得该子图包含了给定的特定节点（称为正则节点）以及其他节点（称为Steiner 节点）之间的最小连接。该问题是一个NP 难问题[5]，其求解难点在于该类问题很难找到多项式时间内的算法，且随着问题规模的增加，通常具有指数级别的解空间。因此，对于这类问题，研究者通常致力于寻找高效的求解方法。

目前，求解该问题的算法主要分为三类：（1）启发式算法，主要有禁忌搜索算法[6]、KMB（Kou Mrakousky Bermaa）算法[7]、MPH（minimum cost path heuristic）算法[8]、ADH（average distance heuristic）算法[9]、Physarum启发式算法[10]等，该类算法在较短的时间内可以找到问题的可行解或次优解，适用于大规模问题，但利用该算法求解STP 时解的质量无法保证。（2）信息传播算法（belief propagation algorithm，BP）[11]，该算法可以作为STP 的消息传递求解器，允许并行计算，因此在处理大规模问题时有一定的效率。但是Steiner 树实例中可能会存在回路，使得算法收敛性变得相对复杂。（3）智能优化算法，如遗传算法（genetic algorithm，GA）[12]、粒子群优化算法（particle swarm optimizer，PSO）[13]、协同进化算法（co-evolutionary algorithms）[14]均为著名的智能计算工具，被广泛应用于各种Steiner树优化问题中。但该类算法易陷入局部最优，且基于树的遗传算法会产生非法的后代树，为确保后代树的连通性，必须采用全局链路信息，计算量大。

现有关于求解STP的算法对比分析较少，因此本文将分别从STP的研究发展、已有算法的概念、基本原理、改进策略及改进前后算法的优缺点展开综述。首先，对相关背景知识进行介绍，梳理STP的发展；其次，对启发式算法、信息传播算法、智能优化算法等经典算法在Steiner 树中的应用进行概述；最后，基于上述提出的算法，分析其研究趋势，总结全文。

1 相关背景介绍

最优Steiner树问题已广泛应用于各种算法大赛，如在2014 年举行的第11 届DIMACS 挑战赛和2018 年PACE 挑战赛中，加强了Steiner 树的普遍适用性和相关性。STP仍然吸引着来自许多学科的研究人员，包括应用数学、计算机科学、运筹学和管理科学等。

1.1 Steiner树问题的发展

Steiner树问题是以Jakob Steiner名字命名的，通过引入一些辅助节点来生成一组具有最小权重的树。该问题根据两个节点之间权值的确定方式，存在多种变体问题。如欧式Steiner 树问题、绝对距离Steiner 树问题和图的Steiner 树问题等，其中图的Steiner 树问题是研究最多的组合优化问题之一。这些变体增加了问题的复杂性，同时该类问题很难寻找合适的Steiner 节点组合，这导致了搜索空间呈指数级增长。总之STP具有高度的复杂性和计算难度，其求解涉及到图论、组合优化以及算法设计等多个领域。

目前，关于Steiner树问题的研究已取得一些重要进展，如吕其诚[15]使用快速算法求解图的Steiner 树问题，随后又对其进行改进，降低了算法的复杂性。Biazzo等人[16]在2012 年提出解决图中获奖Steiner 树问题的空腔法，分析了Goemans-Williamson启发式算法和DHEA求解器，这是一种基于分支和整数线性规划的方法。比较结果表明，在大多数情况下，空腔法在运行时间和解的质量方面均优于前两种算法。Lai等人[17]在2017年对求解Steiner 树问题的进化算法（evolutionary algorithm，EA）进行性能分析，该算法是一种通用且流行的随机算法，并揭示了（1+1）EA在解决一类特殊准二部图的度量Steiner 问题时近似比为3/2，该算法可以有效地找到STP实例的全局最优值。但在构造Steiner树实例时，该算法需要指数级的优化运行时间，意味着（1+1）EA在解决STP时效率低下。近些年关于STP的研究发展如图1所示。

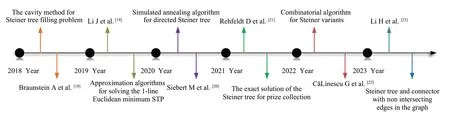
图1 关于Steiner树问题的研究发展Fig.1 Research and development of Steiner tree problem（STP）

1.2 问题描述及公式化

定义1最优Steiner树问题指：给定一个无向图G=(V,E)和权值函数w:E→R+，其中V和E分别表示节点和边的集合。设P(P⊆V)为终端集合（又称正则节点），S⊆VP为非正则节点集合（又称Steiner 节点）。STP的目标是找到一个跨越终端集合P，且边的权值之和最小的生成树。若|P|=2，则将该问题简化为“最短路径问题”；若|P|=|V|，则简化为“最小生成树问题”。记|V|=n,|E|=l,|P|=m,r=m-n。如图2 展示了STP 的一个实例，其中图（a）为原始的无向加权图G，图中红色节点为正则节点；图（b）为最优Steiner树，其中蓝色节点为Steiner节点。

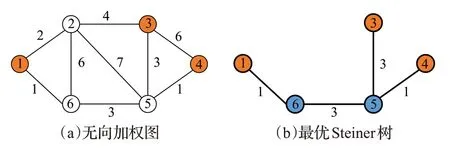
图2 STP实例Fig.2 STP instance

1.3 数学性质

性质1度为0 或1 的非正则节点一定不在最优Steiner树中。

性质2与度为1 的正则节点相邻的点一定在最优Steiner树中。

性质3对于度为2的Steiner节点v，若其相邻的两个节点vi和vj间有边，且w(v,vi)+w(v,vj)＞w(vi,vj)，则最优Steiner树中不包含节点v。

性质4正则节点v的度为2时，若其相邻的两个节点vi和vj均为正则节点，则min{w(v,vi),w(v,vj)}对应的边一定在最优Steiner树中。

2 求解Steiner树的启发式算法

2.1 MPH算法

MPH算法借鉴了最短路径和最小生成树的算法思想[24]，其步骤如下：

步骤1任意选择一个节点v1,且v1∈P。设置i=1,则Ti={v1},Vi={v1}。

步骤2查找节点vi∈S-Vi-1(i=2,3,…,m)，使得vi到Ti-1的权重之和最小，且vi通过最短路径Path(vi-Ti-1)连接到Ti-1,Ti=Ti-1∪Path(vi-Ti-1),Vi为Ti的节点集，最终得到的树为TMPH。

2.2 改进的MPH算法

上述启发式算法通过最短路径来添加正则节点，但最短路径的选择不具有唯一性，使得形成的Steiner树不一定最优。因此，余燕平等人[25]提出基于关键节点的启发式算法（KBMPH）。该算法是对MPH算法的改进，把含有较多最短路径经过的节点称为关键节点，通过对含较多关键节点的路径费用进行修正，然后添加到Steiner树中，其步骤如下：

步骤1求G中所有节点对间的最短路径，若最短路径经过某个节点，则该节点的权值加1，找出权值最大的k个节点，加入节点集M中。

步骤2从P中任选一个节点v1，设i=1，则初始生成树Ti={v1},Vi={v1}。

步骤3对于vi∈S-Vi-1(i=2,3,…,m)，使得vi到Ti-1的修正费用d′(vi,Ti-1)最小，若路径经过一个以上M中的节点，则将路径费用乘以系数λ后再做比较(0＜λ ＜1)。且vi通过修正费用最短路径Path(vi-Ti-1)连接到,Vi为Ti的节点集，最终得到的树为TKBMPH。

KBMPH 算法实现了链路共享，在性能方面进行了改进，但该算法选择的关键节点不一定是Steiner 节点，因此时间复杂度较高。在此基础上，2015年王小龙[26]提出基于加权节点的启发式算法（NWMPH），通过对所有Steiner节点构造权值计算的加权公式，根据权值修正路径费用，用最短路径连接所有正则节点，得到最优Steiner树，改进后的算法在时间复杂度上优于KBMPH 算法，其步骤如下：

步骤1对Steiner节点进行权值计算，公式如下：

通常取0.1 ≤β≤2,0.4 ≤α≤0.8。f(i)为节点i在图中的重要程度，F为f(i)的最大值。di表示节点i的度。gi表示正则节点间最短路径经过节点i的次数。li表示节点i与正则节点直接相连的次数。修正费用d′(vi,Ti-1)=λ×d(vi,Ti-1)，其中λ是所有Steiner 节点权值的平均值。d(vi,Ti-1)是vi到Ti-1的最短距离。

步骤2初始化T1={v1},V1={v1}。

步骤3将vi通过修正费用最短路径Path(vi-Ti-1)连接到Ti-1,Ti=Ti-1∪Path(vi-Ti-1),最终得到的树为TNWMPH。

2.3 Physarum启发式及其改进算法

Physarum启发式算法（Physarum optimization algorithm，POA）是一种基于粘菌体行为的优化算法，模拟了粘菌体在寻找食物的过程中所表现出的集体智能和自组织行为。其智能行为主要有[27]：寻找最短路径、建立高质量的网络、适应不断变化的环境。Physarum是一种单细胞粘菌，能够形成网络并与其他Physarum 生物融合，并行搜索问题的解空间，每个个体收集信息形成问题的部分解，个体间相互融合并共享信息，以找到问题的全局最优解。

近年来，基于Physarum 生物的启发式算法发展迅速，并有研究证实了该类算法能够解决旅行商、最短路径、Steiner 树等各种NP 难组合优化问题[28]。如Liu 等人[29]在2013 年提出基于生物学的Physarum 优化算法，用来求解Steiner 树问题。利用Physarum 生物群体，找到终端集并相互融合，共享智能行为信息，以寻找最优Steiner 树，并将该算法与近似算法，禁忌搜索等经典算法进行对比，结果表明：在大多数情况下Physarum优化算法都能达到与经典算法相近的性能。此外，该算法具有低复杂度和高并行性，但无法保证问题解的质量，在实际应用中需要进行多次迭代，收敛速度慢。在此基础上，Sun等人[30]在2019年提出多源单汇Physarum优化和分层多源单汇Physarum优化两种Physarum启发式算法（Physarum-inspired algorithms，PAS）来解决图的Steiner树问题。用VLSI设计实例来评估PA的性能，对于具有数百个节点的实例，第一个PA 可以找到平均误差为0.19%的可行解，并与遗传算法、粒子群优化算法进行对比分析，结果表明：该算法在求解图的Steiner 树问题时可以取得较好的效果。对于多达数万个节点的较大实例，GA、PSO 和第一个PA 太慢无法使用，而第二个PA可以找到平均误差为3.69%的可行解。

针对启发式及其改进算法进行对比，总结算法原理及优缺点，具体分析如表1所示。

3 求解Steiner树的信息传播算法

近年来，BP算法发展迅速，该算法是基于传统物理学的空腔法，也是一种基于因子图的消息传递求解器[31]，用于给定图形模型（graphical model，GM）表示的联合分布中的最大后验概率分配（MAP）。单个实例的空腔法的优化版本称为Max-Sum 算法，过去已应用于STP 及变体问题。Braunstein 等人[11]通过空腔法优化STP，描述了Max-Sum 方程的两个增强功能，以便能够解决现实世界实例的优化。第一个是开发一种替代“平面”的模型公式，允许减少相关配置空间，使该方法在实例上可行，特别是当正则节点数量较少时。第二个是Max-Sum算法和贪婪启发式算法间的集成，这种集成是将Max-Sum 转换为一种极具竞争力的自包含算法，其中在迭代过程的每一步都给出了可行解。

3.1 图形模型

定义2n个（二进制）随机变量的联合分布Z=[Zi]∈{0,1}n被称为图形模型：

其中，{ϕi,ϕα}为给定的非负函数，称为因子。如图3描述了因子Fi和变量zi之间的图形关系，Fi={α1,α2,α3},n=4,。

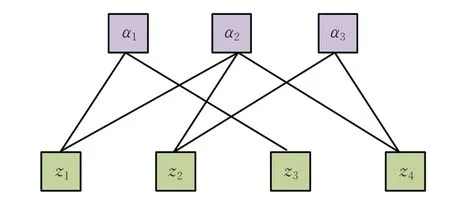
图3 因子Fi 和变量zi 之间的图形关系Fig.3 Graphical relationship between factor Fi and variable zi

对于给定的一组消息，BP边际信念计算如下：

如果因子图是树且MAP 分配是唯一的，则zBP收敛于MAP分配。如果图中存在循环，BP算法一般不能保证找到MAP赋值。BP算法的具体描述如下：

算法1BP算法

输入：构造初始化因子图模型，最大迭代次数为tm。

输出：算法收敛后得到不动点。

3.2 Steiner树的变体问题

最优Steiner树存在多种变体和推广问题，本文主要区分了顶点不相交的Steiner树问题（Steiner tree problem with disjoint vertices，V-DSTP）与边缘不相交的Steiner树问题（Steiner tree problem with disjoint edges，E-DSTP）。在V-DSTP中，不同的树不能共享节点，因而也不能共享边；在E-DSTP中，边不能被树共享，而节点可以由不同的树共享。这些额外约束的引入，增加了算法设计的难度，使得问题更为复杂，且该问题均为NP难问题[32]。这两个变体的应用通常涉及到需要满足特定约束条件的网络或布局设计问题。如在实际应用中，V-DSTP可以用于通信网络设计，以提高网络的可靠性；E-DSTP 可以用于流水线布局，以提高生产效率。基于该问题的求解难度与广泛实用性，研究人员进一步探索深度学习和机器学习方法在Steiner 树变体问题中的应用，从而提高求解效率。

如图4和图5分别表示两种变体问题使用分支模型的可行赋值。方形节点表示根节点，圆形节点表示终端节点，箭头表示边缘被使用，标签表示（正）深度分量的值。图4 为V-DSTP 变量的可行赋值，包含两个子图；图5为E-DSTP变量的可行赋值。

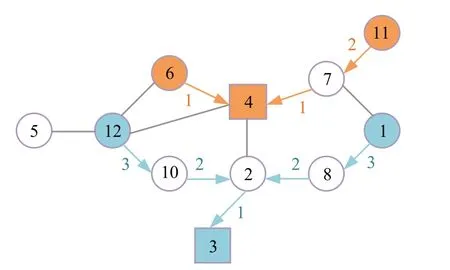
图4 使用分支模型对V-DSTP的变量的可行赋值Fig.4 Feasible assignment of variables to V-DSTP using branching model

图5 使用分支模型对E-DSTP的变量的可行赋值Fig.5 Feasible assignment of variables to E-DSTP using branching model

为了强调分支模型（branching model）和平面模型（flat model）的区别，如图6和图7分别描绘了分支模型和平面模型在网格图上对V-DSTP相同解的情况。图6根据分支形式，需要d=7 的最小深度，以允许“蓝色”通信的所有终端到达根节点“1”；图7根据平面形式，需要d=3 的最小深度。事实上，当每次到达一个终端节点，或分支点时（如图中节点“23”附近），深度变量增加一个单位。

图6 使用分支模型时V-DSTP的解Fig.6 Solution for V-DSTP using branching model

图7 使用平面模型时V-DSTP的解Fig.7 Solution for V-DSTP using flat model

3.3 信息传播方程

对于图G其顶点与边分别具有非负奖励和正权重,STP的目标是寻找M个连通子图，该子图Gμ=(Vμ,Eμ)跨越不相交的终端集{Pμ⊆Vμ,μ=1,2,…,M}，使以下成本函数最小：

为了解决上述两个组合优化问题，在与图G相关的因子图上定义一组适当的相互作用变量。因子图是因子和变量的二部图。若函数依赖于变量，则因子和变量之间存在边。对每个节点i∈V和每条边(i,j)∈E，分别关联一个因子节点ϕi和一个二分量变量{(dij,μij)∈{-D,…,0,…,D}×{0,…,M}}，其中dij为深度，μij为通信变量，用来标记形成不同树的边缘。将Steiner 树的每个解映射到相关因子图的变量d={dij:(i,j)∈E} 和μ={μij:(i,j)∈E}的某个赋值上。则式（8）可以用新变量表示为：

BP方程为：

其中，Zij是归一化常数；δij是Kronecker Delta 函数；mij为消息，表明一些信息在因子图的边(i,j)上从节点i向j流动。上式也可以看作是可迭代求解的不动点方程组，从t=0 时的一组初始消息开始迭代公式的右边，直到数值收敛到一个不动点。

3.4 BP算法的收敛性与正确性

关于BP算法的收敛性与正确性已经取得了一些显著的研究成果，但当问题规模增大时，树状因子图的结构复杂，使得算法的收敛速度变慢。文献[33]给出BP算法的收敛性和正确性准则，GM的最大后验概率分配对应于LP的最优解。此外，如果LP的解是唯一的，则GM上的最大乘积BP 具有唯一不动点。文献[34]中为了分析BP算法的收敛性，通过对消息更新方程取双曲正切，将消息取值从[0，1]扩展为(-∞,+∞)，利用压缩映射原理证明了BP算法收敛的充分条件。

4 求解Steiner树的智能优化算法

智能优化算法是一类基于自然界的生物进化、群体行为等思想，通过模拟和引入这些思想来解决问题的计算方法。近年来也用于求解Steiner 树及变体问题，如Dehouche[35]描述了遗传算法在最小标记Steiner 树问题中的应用，引入了一类新的有效不等式，评估其在解决该问题时的性能，给出最小标记Steiner树问题的整数线性规划公式，以及用于加速分解过程的有效约束条件，并将新的方法与进化算法进行比较。Camacho-Vallejo等人[14]提出求解电信网络中分层Steiner 树问题的协同进化算法，在该网络中将集线器之间的连接视为Steiner树，并把Steiner 树问题建模为双层数学规划模型，以降低网络连接成本。此外，开发了两种协同进化方法来解决该双层模型，总结出上述方法的优缺点，并证明其有效性。

4.1 粒子群优化算法

粒子群优化（particle swarm optimizer，PSO）算法是模拟鸟群或鱼群等群体行为的智能优化算法。种群中的每个粒子表示解空间中的一个潜在解，通过不断更新粒子的位置和速度来搜索最优解。刘耿耿等人[36]提出基于混合离散粒子群优化的Slew 约束下X 结构Steiner最小树算法。使用预处理方法，节省电压转换速率的计算，设计了一种高效的混合修正策略，使得Steiner最小树能够完全满足Slew约束。该算法与同类算法相比，实现了最佳的布线结果。刘庆等人[37]提出求解最优Steiner 树的前驱编码粒子群优化算法，避免了环的产生。分别基于邻接矩阵和剔除相同适应度值粒子策略，设计了“开发”算子和“勘探”算子，进一步提高了算法的全局搜索能力。

具体说来，设种群规模为N，其中每个粒子都是一个d维向量，其在目标搜索空间中的位置可以表示为xi={xi1,xi2,…,xid},i=1,2,…,N,速度可以表示为vi={vi1,vi2,…,vid},i=1,2,…,N。记pbest表示当前粒子的历史最优值，gbest表示全局最优值。当前粒子根据以下速度更新公式和位置更新公式进行状态更新：

其中，下标ij表示粒子i的第j维；t为迭代次数；ω为惯性权重；c1,c2为加速常量；r1,r2为随机数，通常在[0，1]范围内取值。对于给定的无向图G=(V,E)，利用PSO算法求解最优Steiner树的基本步骤如下：

4.2 遗传算法

遗传算法是一种模拟自然界生物繁殖和进化过程的全局搜索算法。由四个主要元素组成，即染色体编码/解码、个体适应度评估、遗传算子和操作参数。Haouari等人[38]提出一种用于奖品收集Steiner 树问题的混合拉格朗日遗传算法。下界是基于问题的最小生成树公式的拉格朗日分解，体积算法用于求解拉格朗日对偶。遗传算法结合了多项增强功能，充分利用了拉格朗日分解产生的原始和对偶信息。但是，现有用于求解STP的遗传算法由于不连通、存在循环和正则节点缺失，可能导致产生非法解。因此，Diveev[39]提出了一种避免组合优化问题非法解的有吸引力的方法：在有限范围内通过迭代搜索一个基本解的微小变化，以找到更好的解。

Steiner 树优化问题中的遗传算法交叉机制已广泛应用于经验建模、决策树、多项式符号回归、数据分类、语法树等领域[40]。现有Steiner树优化问题的GA根据染色体的表示可以分为以下两类[41]：

（1）直接编码树的遗传算法交叉机制（DT）。树作为染色体，在交叉过程中，随机选择两条父染色体，将相同的链路和正则节点复制到子代。这些节点和链路通常是一系列分离的子树，采用Prim、Dijkstra[42]等最短路径算法迭代连接两个随机选择的子树，直到所有子树全部连通。

（2）间接编码的遗传算法交叉机制。在Steiner树优化问题中，该机制分为两种[43]：第一种是Prüfer 编码，字符串交叉操作采用两点交叉，父字符串在两个随机选择的位置上交换基因片段，通过解码生成的新字符串得到后代树；第二种是序列和拓扑编码（ST），先将树转化为位置索引树，再进行编码。但这类遗传算法可能会产生非法后代树，因此，需要一个检测程序和带有贪婪算法的修复函数来保证后代树的合法性，降低了算法的有效性。

4.3 改进的遗传算法

Huy 等人[44]提出求解图中Steiner 树问题的并行遗传算法，基于二进制编码，利用启发式算法来评估个体的适应度，并与其他元启发式算法进行对比。王小龙[26]通过结合模拟退火算法与遗传算法提出求解STP 的混合遗传算法，通过对每一代的最优个体进行模拟退火操作，增强算法的局部搜索能力。Zhang 等人[45]给出一种新的Steiner 树优化遗传算法交叉机制，称为LC 机制。该交叉机制不需要全局链路信息，编码/解码以及修复操作，只需交换部分父染色体就可以产生合法的后代树。在不同规模的网络中，使用叶交叉机制的遗传算法不仅能产生更好的解，而且收敛速度更快，优于现有交叉机制的遗传算法。

4.3.1 LC机制的两个过程

定义3在无向图G中，源节点集为D，正则点集为R,link(u,v)∈E表示连接节点u和v的直接链路，则{D}∪R⊆V。设Π={T1,T2,…,Tj,…,Tn}表示问题的解空间，其中Tj={Vj,Ej}⊆G,Vj⊆V,Ej⊆E,对于∀Tj⊆Π，设：

Steiner树优化问题表示如下：

（1）若边上无约束，有min{w(T):T∈Π}，质量函数F′(T)=w0-w(T)，w0为足够大的常数，使F′(T)为正。

（2）若边上有约束，Ci(u,v),i=1,2,…,k,k≥1 表示约束的量化指标。设

优化问题表示为：min{w(T):T∈Π} ，约束为：Ci(T)≤ci0,i=1,2,…,k，其中ci0是约束Ci的阈值。

对于给定的树T1、T2，LC机制主要有两个过程：

过程1LC机制为D添加链接(D,-1)，并将相同链接复制到后代树中：newT={V(E1∩E2),E1∩E2} 。这一过程类似于DT 遗传算法，避免了编码、解码操作，并以叶节点作为切入点，从剩余链路中选择关键的高质量链路。

过程2首先在newT中添加高质量的路径，再删除父树中的冗余链接。从leaf1∩leaf2中随机选择一个节点v，并分别在T1、T2中找到从v返回D的路径P1、P2。选择连接点u将路径连接到newT。定义Child(ET)={v|link(v,u),link(v,u)∈ET}，其中VP表示P中的节点，u满足：μ∈Child(EnewT)∩VP。若Child(EnewT)∩VP有多个节点，则选择距离叶节点最近的节点作为u，并切割路径仅保留叶节点到u之间的链路。最后，比较P1,P2的质量，将较好的路径添加到newT，再从父树中删除P1,P2。综上，一次完整的LC 过程迭代结束，LC的下一次运算只需选择一个相同的叶节点v∈leaf1∩leaf2，重复上述操作。

4.3.2 基于LC遗传算法的实现

该算法以树作为染色体，避免了编码/解码操作。与现有交叉机制不同，LC 通过交换部分父染色体来产生后代树。以父树中的叶节点作为切入点，将父染色体分解成若干条路径，比较具有相同叶节点对应的两条路径，将较好的路径添加到后代树中。并从合法后代树和时间复杂度两个方面说明了该算法的有效性，证明了LC机制可以生成合法子树，且不需要最短路径算法、检测过程、修复函数、全局链路信息和编码/解码等操作。具有适应性广、计算量小、实现收敛所需的平均适应度评估次数少的特点，表明了LC 比其他交叉机制更有效。其算法原理如下：

（1）适应度函数：若边上无约束，则取函数F′(T)作为适应度函数。若边上有约束，约束Steiner树优化问题的一种常用方法是在适应度函数中使用惩罚技术。树T的适应度函数表示如下：

其中，α是惩罚因子，通常限制在区间（0，0.5]内。

（2）选择：目前广泛使用的选择方案有比例选择。

（3）交叉和变异：文献[46]给出一种新的遗传算法变异方案。根据变异概率Pm随机选择一个节点子集，通过删除与所选节点相关的所有链路，将树分解成若干个独立的子树。然后，随机选择一条权重最小的路径，将这些分离的子树连接成一棵新的树。

4.3.3 各种交叉机制的性能分析

分析文献[45]，并总结各类交叉机制的算法性能。取G1=（50，63，13）、G2=（50，63，25）、G3=（50，100，13）、G4=（100，125，17）、G5=（100，200，17）、G6=（100，200，50）、G7=（500，1 000，83）、G8=（500，2 500，83）8组实例数据，分别表示节点数、连接数和正则节点数。交叉概率与变异概率分别为Pc=0.6 和Pm=0.05。如表2 统计分析了各类交叉机制的GA 在小规模图上随机生成1 000个后代树的性能，种群规模M=100。

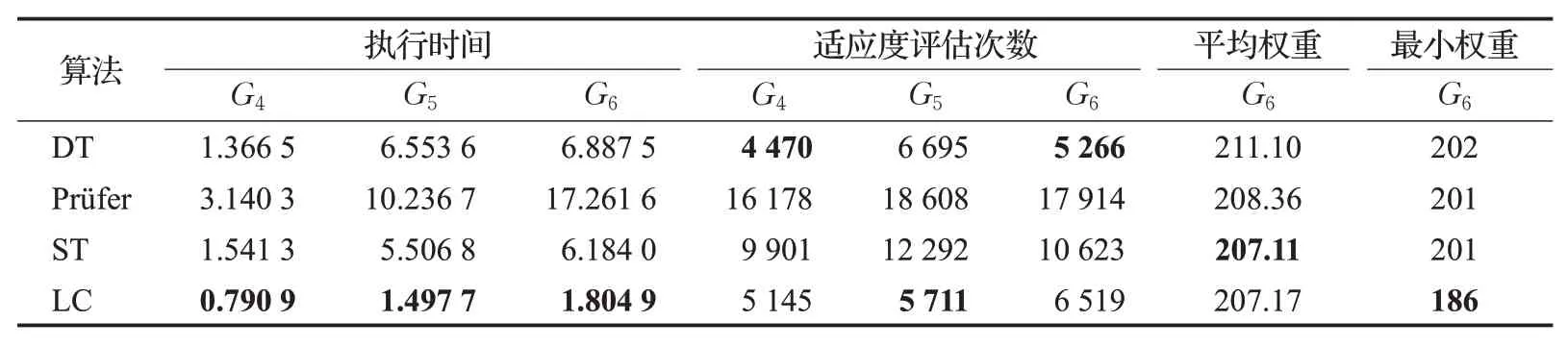
表2 小规模图上的性能对比分析Table 2 Performance comparison analysis on small-scale graphs

从表2可以看出LC机制的执行时间远远小于其他交叉算子，同时计算了4种交叉机制在G4～G6上实现收敛所需的平均适应度评估次数。Prüfer达到收敛时所需的适应度评估次数最多，ST次之，而LC和DT以相同的速度收敛，适应度评估的次数最少。与其他交叉机制不同的是，DT 的执行时间不会随着网络图的复杂程度而增加，这是因为DT 算法以最短路径算法为主要操作。因此，正则节点的相对位置对执行时间有很大影响，当正则节点之间距离较近时，执行速度较快；当正则节点之间距离较远时，执行速度较慢。最后统计了四种交叉机制在G6上，M=200 时的平均权重和最小权重。可以看出，LC和ST的平均权重几乎相同，而DT和Prüfer的平均权重较大，同时LC在最小权重方面性能更好。

表3 记录了在G3～G5的规模图上，RW+0.6+0.1、RW+0.8+0.05、RW+0.8+0.1不同参数组合下GA的执行时间。从表中可以看出，LC 机制比其他交叉机制需要更少的执行时间，性能优于其他交叉机制。

表3 不同参数组合下遗传算法的执行时间Table 3 Execution time of genetic algorithm under different parameter combinations

如图8是在G1～G3上采用典型参数的GA取得的最佳权重，从图中可以看出，LC机制的遗传算法在G1～G3上的权值均小于其他交叉机制，表明在此规模上LC 机制的性能最好。

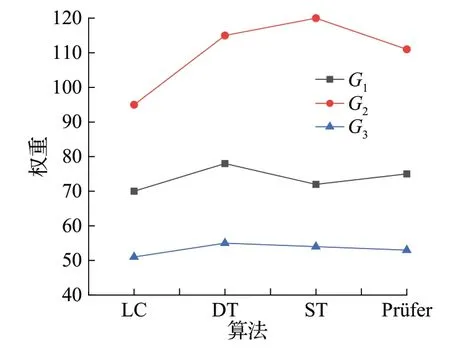
图8 GA在典型参数下的权重Fig.8 Weight of GA under typical parameters

如图9（a）、（b）分别记录了GA 在G7、G8规模上生成前30代获得的最佳权重。从图中可以看出，DT算法收敛速度最快，ST 次之，而LC 收敛速度最慢。这是由于LC 的时间复杂度与父树的长度成正相关，而与图的大小无关。所以使用LC 机制的GA 可以达到30 代，而其他机制的遗传算法只能达到1～2 代。这个特点使得LC 很容易采取额外的措施，如扩大种群规模或提高变异概率，以获得更好的解。

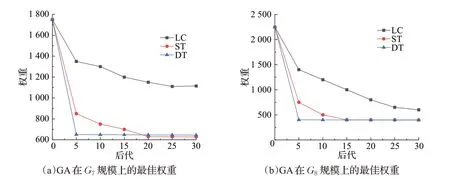
图9 大规模图上GA的最佳权重Fig.9 Optimal weight of GA on large-scale graphs

关于遗传算法不同交叉机制的分析如表4所示。

表4 不同交叉机制的对比分析Table 4 Comparative analysis of different crossover mechanisms

4.4 智能优化算法的性能对比

针对智能优化算法及其改进算法进行对比，总结各算法的原理及优缺点，具体的算法性能分析对比如表5所示。

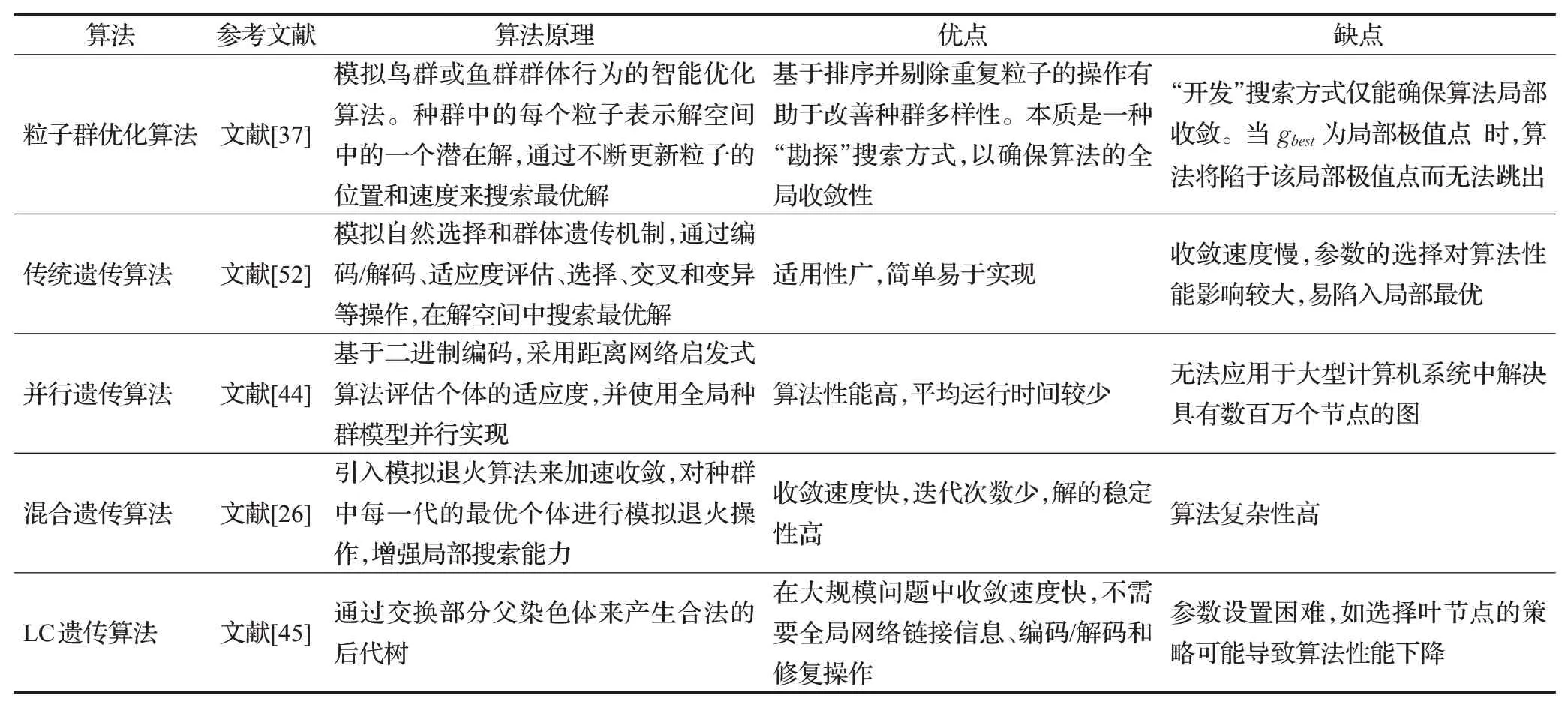
表5 智能优化算法及其改进算法的对比分析Table 5 Comparative analysis of intelligent optimization algorithms and their improved algorithms

5 结束语

本文详细介绍了启发式算法、信息传播算法、智能优化算法的相关知识，对Steiner树优化实例的求解进行概括，从交叉机制、收敛速度、有效性等方面进行综述，给出求解最优Steiner 树问题的算法研究趋势和发展方向。Steiner 树及其变体问题具有高度复杂性，且为NP难问题。在实际应用中，往往存在多个冲突的优化目标，如最小化成本、最小化延迟等。针对大规模问题，传统的求解方法可能会变得非常耗时，甚至不切实际。尽管对于Steiner树优化问题的研究已取得了一些进展，但仍存在许多挑战和待解决的问题，如在考虑实际约束的同时，如何设计快速有效的算法以在合理的时间内找到全局最优解；针对大规模问题时，如何提高算法的可伸缩性。由于LC是基于Steiner树的GA中第一个未使用贪婪算法的交叉机制，大大减少了计算时间。因此，未来的工作应聚焦于探索结合不同算法和技术的新方法，以进一步提高解的质量和求解能力，并研究GAS和LC在其他实际中的应用，如SMT、组播通信和传输路由设计等。