应用优化建模法构建红松人工林单木直径生长模型1)

吕洁 童茜坪 金星姬 Timo Pukkala

(东北林业大学,哈尔滨,150040) (东芬兰大学)

红松(Pinuskoraiensis)是我国东北林区重要的地带性顶级群落物种[1],据第九次全国森林资源清查显示,我国红松人工林面积为3 091 hm2,蓄积量为264.20 m3。黑龙江作为红松的故乡,面积占全国的比例为48.59%,蓄积量占全国的比例为61.27%,每公顷蓄积量为107.77 m3,较第八次清查结果提高了近25%[2]。黑龙江省的红松人工林已进入近熟林阶段,为了预测人工红松近成熟龄的生长规律,Jin et al.[3]构建了人工红松的单木生长基础模型,用于人工红松的多目标经营优化,由于前期建模数据的龄组范围窄,对人工红松的蓄积量模拟结果过高。根据单木模型的林分生长模拟,主要包括立地指数、树高曲线、单木直径生长、存活和削度方程等基础模型,其中最重要的模型是单木直径生长模型[4-9]。应用到人工林经营的主要模型是与距离无关的单木生长模型[10-12],与距离有关的直径生长模型通常用于对天然林、混交林进行林分生长模拟[13-18]。距离无关的生长模型和距离有关的生长模型对纯林的生长模拟基本相同[19-20],其建模方法是根据胸径生长的多期间隔数据,采用回归法构建林木直径生长模型[21-22]。在实际林业调查中,多期复测数据往往存在测量间隔不等、同木异号、漏测、错测等问题[23],导致利用回归法构建的直径生长模型的前提假设有偏差,即间隔期内的直径生长率恒定。优化建模法有效解决了回归法建模存在的问题,并成功应用到挪威云杉(Piceaasperata)、白桦(Betulaplatyphylla)、落叶松(Larixolgensis)等树种的单木直径生长模型的构建[24-26]。为进一步提升优化建模法的预测精度,在探究优化法损失函数的可靠性的同时,与传统回归法构建的直径生长模型进行比较分析,为制定科学、有效的森林经营方案提供可靠的模型基础。

1 研究地概况

研究地坐落于黑龙江省东北部的孟家岗林场、红旗林场、青山林场、帽儿山林场和凉水自然保护区,地理坐标地跨东经121°11′～135°5′,北纬43°25′～53°33′(见图1)。该地属于温带大陆性季风气候,年平均气温3.1 ℃,年降水量629 mm,降水多集中于6—8月份,雨量充沛。林区主要土壤类型为暗棕壤、白浆土、草甸土,土壤肥沃。主要乔木树种有红松(Pinuskoraiensis)、落叶松(Larixgmelinii)、樟子松(Pinussylvestris)等,主要灌木树种有刺五加(Acanthopanaxsenticosus)、山槐(Maackiaamurensis)、五味子(SchisandrachinensisTurcz.)等。

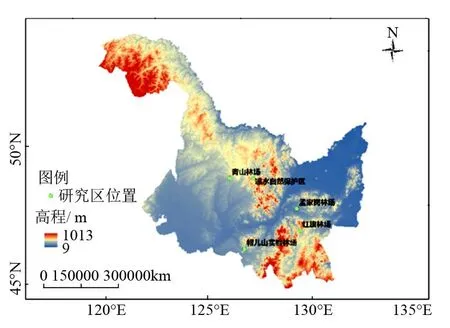
图1 研究区域林场分布图

2 研究方法

2.1 数据来源

建模数据来源于1980—2022年内不规则测量间隔期固定样地数据,剔除样木复位率低、错测漏测木过多的样地和采伐样地,共筛选出符合建模要求的红松人工林固定样地75块(7 235株活立木),共测量362次。样地测量间隔为1～6 a,样地面积为0.06～0.16 hm2。统计各样地的初次单木、林分因子和立地因子。林分因子包括林分平均胸径、优势高、林分密度和每公顷断面积等,单木因子包括单木胸径、树高及大于对象木断面积之和,立地因子用地位指数表示(见表1、表2)。

表1 红松人工林林分统计量

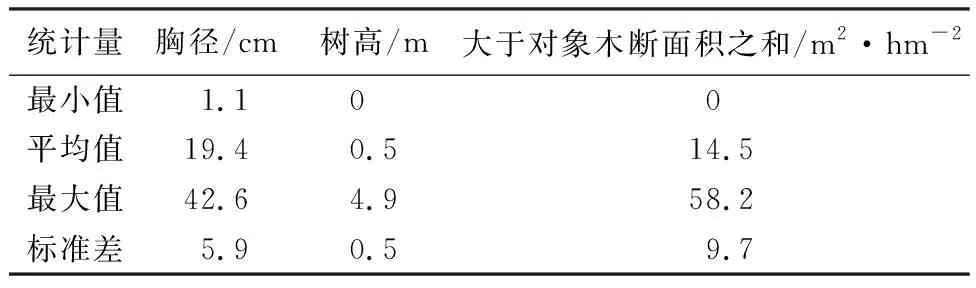
表2 红松人工林单木统计量

2.2 传统模型的构建

2.2.1模型的影响因素选择

研究采用逐步回归法和相关性分析依次将林木大小因子、林木竞争因子与立地指数键入模型[27],构建的3个基础模型。模型表达式如下:

id=F(α+Fsize);

id=F(α+Fsize+Fcomp);

id=F(α+Fsize+Fcomp+SI)。

式中:id为对象木的单木直径增量,α为模型截距,Fsize为林木大小因子函数,Fcomp为林木竞争因子函数,SI为立地指数。

2.2.2模型目标函数及求解方法

在构建单木直径生长模型时,采用传统分析方法—最小二乘法(OLS)[28]。最小二乘法是一种统计学上的回归分析方法,它可以将模型中的参数进行优化,使模型的预测值与实际观察值之间的误差平方和最小化,这种方法在提高模型预测精度和有效处理样本数据中存在的异方差问题方面具有显著优势。本研究依据最小二乘法得到一个较为精确的传统模型,从而描述树木直径的生长过程和规律。

最小二乘法目标函数如下:

2.2.3模型评价与检验

通常从生物学角度对模拟的图像进行分析以及从统计学角度判断模型优劣,包括模型影响因素与直径生长的正负相关性,参数显著性(P<0.05),影响因素之间的多重共线性检验-方差膨胀系数(VIF<10)及模型决定系数(R2)、平均偏差(Bias)、平均绝对误差(MAE)、均方根误差(RMSE)、赤池信息准则(AIC)等指标。

模型拟合精度检验指标如下:

AIC=2P-2LL;

2.3 优化法模型的构建

2.3.1目标方程的构建

本研究对优化模型拟合方法进行了改进,采用林分密度为权重,利用单纯形法[29]对初始参数(a、b、c1、c2)进行优化,选取不同初始参数的数值排列组合进行测试,并根据参数的组合结果,结合样地实测数据确定最终参数。该方法利用不同测量间隔期树木的直径生长数据,模拟树木的生长,直到下一次测量开始后将模拟得到的直径分布与测量数据进行了比较。目标函数定义为[20,24]:

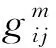
2.3.2求解优化方法

利用单纯形法对目标方程进行优化求解,将最小损失函数视为优化算法的目标函数,通过最小化损失函数,使模型参数不断接近最优解。即先找出可行域的一个顶点,根据规则判断其是否最优,否则,则转换到与之相邻的另一顶点,并使目标函数值更优;如此反复,直至找到最优解为止,以此提高模型的收敛速度和拟合精度。

2.3.3模型的检验

由于本研究没有充足的数据,无法执行重复实验,因此选择重采样方法充分利用所拥有的数据估计标准误差、置信区间和偏差,通常被用作检验模型参数的统计学显著性,能有效解决实验数据样本量不够充分的问题。因此,对单木直径生长模型进行自举法分析检验,样本量的设置根据数据中体现出实际测量样地的数量共抽取了50个随机样本,每个样本包含了36个不规则测量间隔。根据单纯形算法对模拟值进行50次数值优化(额外5次),根据模拟值计算各参数的均值和标准差,并利用t统计量与均值和标准差的比值来评估参数的显著性。

3 结果与分析

3.1 不同方法构建的模型

由表3可知,采用回归法在常数模型的基础上逐步添加或剔除影响因素,随着模型中变量的变化,各项评估的指标也发生着改变。根据相关性分析和回归分析得到以胸径(d)、大于对象木断面积之和(BAL)、胸径断面积(G)、地位指数(SI)为影响因素构建红松人工林单木年均直径生长模型。单木直径生长模型如下:

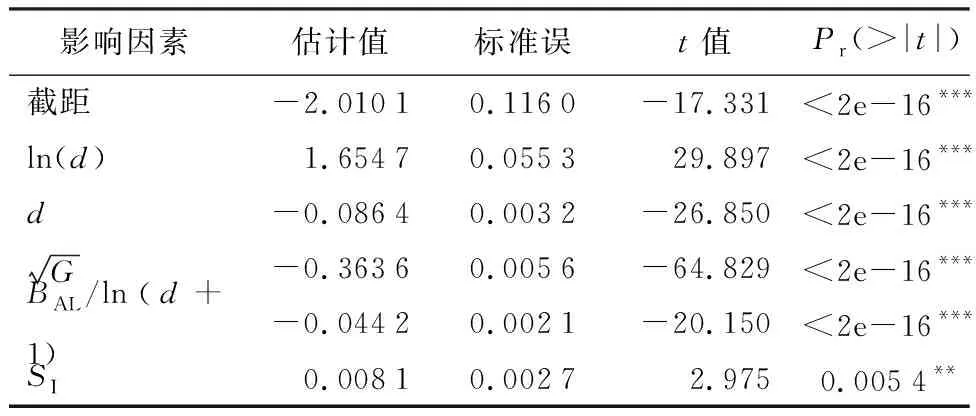
表3 不同影响因素最优传统模型拟合结果

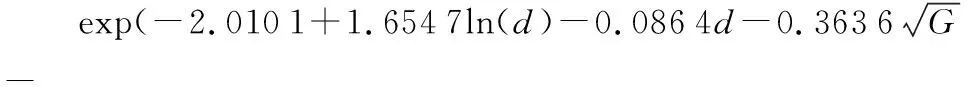
式中:id为年均直径生长量,d为胸径,G为林分断面积,BAL大于对象木断面积之和,SI为地位指数。

林木的直径生长量与胸径成正相关,表示林木本身大小对林木的生长有着很大的影响,并且促进林木生长。单木直径生长受相邻木竞争的影响,树木初始胸径的大小还代表了其在林分中的竞争状态,即林木初始胸径越大,直径生长量越大。本研究考虑了林分每公顷断面积、大于对象木断面积之和两个竞争因子。初始直径大,树木更容易获得光照、水和土壤养分,但密度过大会导致单木获得养分机会减少,因此直径生长量会随着的林分断面积增大而减小。地位指数是反映立地条件的指标,它与树木生长速度密切相关,直径生长量通常会随着立地条件的改善而增加,良好的立地条件促进树木生长。模型可以较好的解释各影响因素与红松人工林生长量的关系,符合林木实际生长规律。

根据回归法构建的单木直径生长模型统计结果的检验指标对红松单木直径生长模型进行精度评价,模型的决定系数为0.414 9,均方根误差为0.335 1,平均绝对误差为0.250 8,赤池信息准则为16 536,平均偏差为0.01,表示该模型可以解释林分中单木直径年均增量接近一半的变异,另一半变异由于气候和收集数据的误差引起,在林业中存在着诸多不确定性,该模型显示对林木生长较强的解释能力,适应效果好。

由表4可知,基于优化法求解最小损失函数,得到单木直径生长模型参数。具体模型如下:

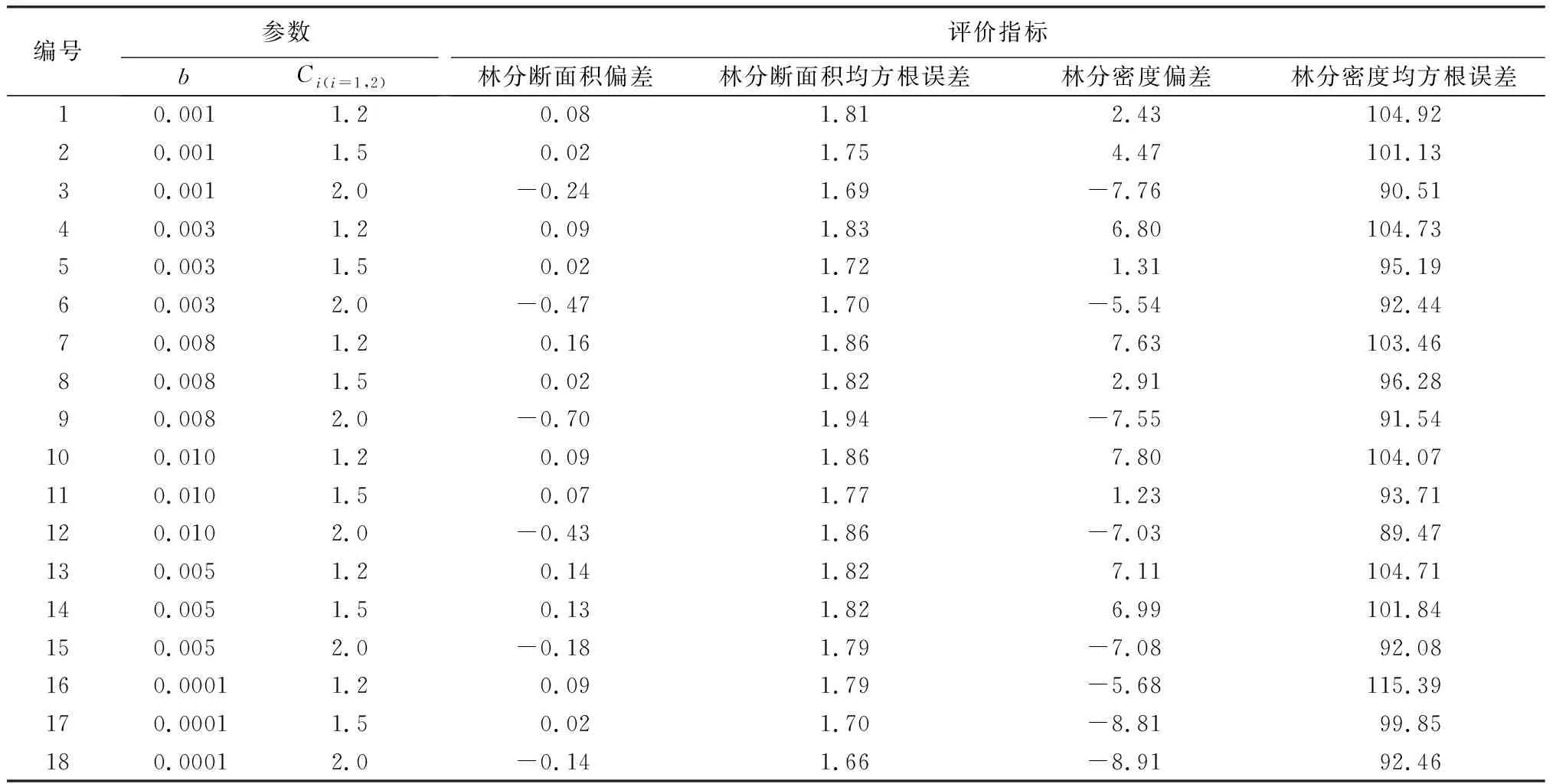
表4 不同参数组合下目标方程的评价指标

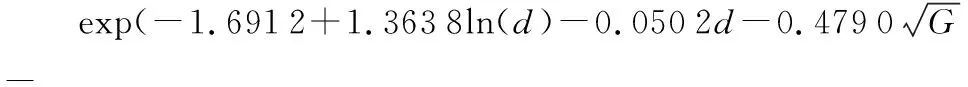
式中:id为年均直径生长,d为胸径,G为林分断面积,SI为地位指数,BAL为大于对象木断面积之和。

根据不同参数组合下目标方程的检验指标,目标方程中a代表林分断面积权重固定值(a=1),b代表林分密度占目标方程的权重,c1和c2分别代表了测量值和模拟值得到的直径分布频率之间的差异增加损失的速度(c1和c2通常为2)[30-31]。根据b、c的不同取值进行排列组合,当b=0.003,c1=c2=1.5时,模型偏差和均方根误差最小。林分断面积偏差总是很小,林分断面积通常由直径直接影响;均方根误差也在可以预见的范围内,虽然统计结果与传统模型相差无几,但从原理上,该法增加了对非固定测量间隔数据的利用,减少了同号异木等测量误差造成的估计偏差。

3.2 模型检验

本文对优化建模法构建的单木直径生长模型设置自举法检验,自举法目的是为了观察不同数量的重复样本和模型拟合结果对结果的影响,评价标准分别有最小值、最大值、平均值和标准差。

由表5可知,模型参数均通过检验。自举法检验的结果是根据优化模型拟合参数组的样本中提取,自举法模型的拟合组成由不同的模型数据组成,表明不同的拟合数据产生了相似的参数估计。通过对比这两组检验所表现出的变异系数,发现两组样本量相异的优化检验过程取得了相似的模型参数拟合结果,这也表明了优化建模得出的模型拟合参数结果科学可靠。

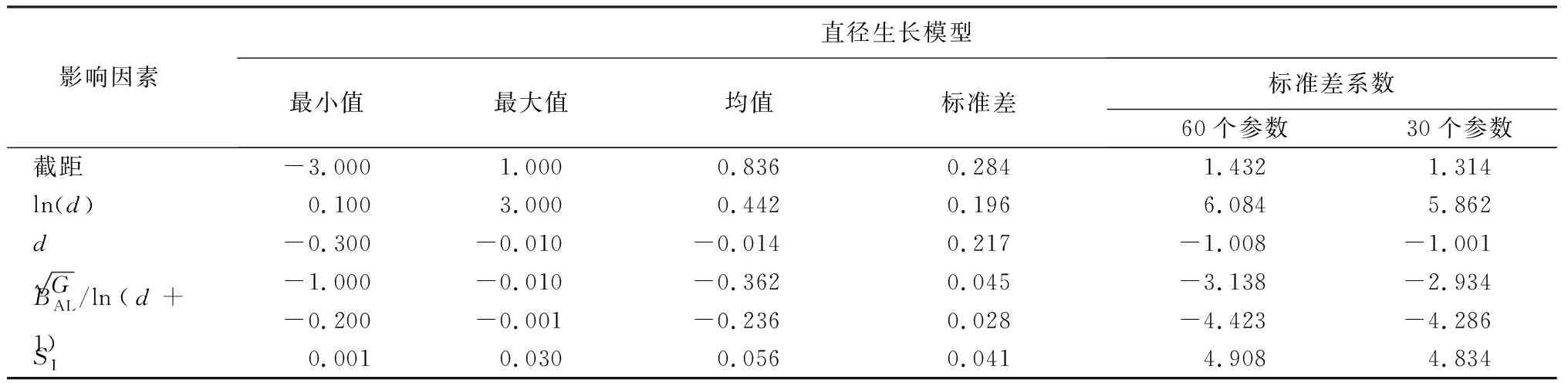
表5 优化模型自举法检验结果

标准差能反映直径生长量的模拟值和实测值的离散程度。所有参数的标准差均小于0.3,表明本研究构建模型的预测值与真实值差距小,能够很好地反映林分的生长规律,验证了模型的科学性和有效性。标准差系数(标准差与平均值的比值)可以消除测量尺度和量纲的影响。在两组数据的测量尺度相差太大时,标准差不合适比较数据的离散程度,标准差系数可以很好的评价数据的离散程度。在单木直径生长方程中,树木的胸径是一个不可或缺的变量,而模型中的两个关于胸径(d)的变量中,胸径可以限制小径材的下限,而ln(d)为防止大径材无限制的增加设置较为客观的上限。

根据模型的参数可知单木胸径和林分断面积对单木直径生长影响较大。当树木密集时,空间较小,林木间竞争较弱时,树木的直径增长缓慢。立地指数与立木生长呈正相关,但影响较小,立地条件对促进林木增长的效果不显著。因此,通过提高红松人工林立地水平改善单木生长水平,花费物力人力得不偿失。

3.3 模型可视化分析

由图2可知,模型的残差随林分断面积和林分密度变化,模型残差值在林分断面积大于35 m2·hm-2,林分密度大于800株·hm-2时分布较为分散,说明模拟幼龄林和老龄林的单木直径生长时会出现较大偏差,而对中龄林红松人工林林分生长状态模拟效果较好。原因是缺乏栽种密集的幼龄林数据及老龄林数据,模型只能根据现有的中林龄数据模拟红松其它生长阶段的林分状态。因此,在利用该模型模拟林分直径生长时,针对中龄林的林分管理措施较为确切,其它林分状态下的单木直径生长值得商榷。此外,根据红松的人工林特性,不能凭借单一指标对人工林单木进行培育或采伐,采用较均匀的林木分布可以提高林地利用率和经济效率。

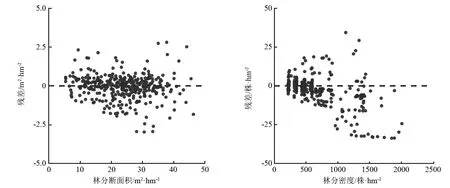
图2 优化模型林分断面积与林分密度残差

由图3可知,分别给出了两组不同建模方法在不同条件下的单木直径增长模拟实验情况。图3A设置的初始条件为各径阶对应的林分断面积由6 m2·hm-2递增至30 m2·hm-2,且各径阶对应的大于对象木的断面积之和以30%的林分断面积计算。此时模型对单木直径年增长量的预测表明,当树木胸径在20 cm左右时,处于该生长阶段(幼中龄林)的林木生长速率较快,生长速率随着自身的成熟度增加(胸径增大)而缓慢减小。

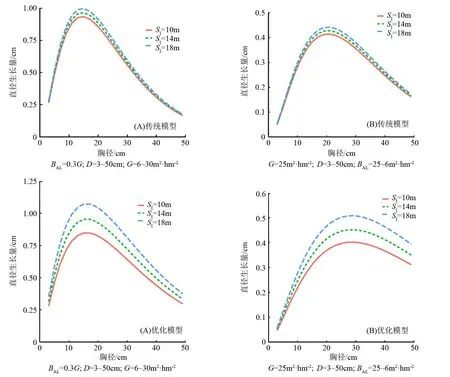
BAL为大于对象木断面积之和,D为胸径,G为林分断面积。图3 不同限定条件下单木直径生长模型的模拟结果

图3B当初始条件设置林分断面积为常量,各径阶对应的大于对象木断面积之和由25 m2·hm-2递减至6 m2·hm-2时。模拟结果展示的曲线走向,幼龄林状态下林木竞争激烈,受到周围竞争木的影响较大,生长缓慢。伴随着林分的发展,森林进入速生期,林分中胸径大的林木生命力强,生长强度大,拥有更好的光照环境和土壤环境。但是当胸径超过一定值时直径生长量下降,此时越来越多的相邻树木成为竞争对手,林内光照减弱,林地阴湿,林木生长又开始变得缓慢,符合林木生长的一般规律。优化建模法得到的模型,立地条件的好坏对林木生长影响显著,立地条件越好,树木生长的速度就越快。

由图4可知,根据红松人工林林分断面积年平均生长变化的模拟结果,构建的模型对林分断面积的生长模拟值的离散程度要比实测值小,并且模拟得到的林分断面积年均增量比实测值略低,且林分断面积的年平均增长量随林分断面积的增加而减小。优化法得到的模型的断面积残差值为0.02 m2·hm-2,明显优于由传统法模型的断面积残差值(0.44 m2·hm-2),精度提升显著。优化法模型与实测值和传统法模拟值相比,优化法模拟值的林分断面积增量随着林分初始断面积的变化被限制在较窄的范围内,由于优化建模的方法最小化与回归分析的目标函数(损失函数)不同,使个别测量值较高的样地数据被目标函数当作不符合判断条件的对象而排除在外,然后再对测量数据进行校准,因此使测量值较高的样地数据无法被引用到模拟生长的计算过程;另一个重要的原因是优化法能同时模拟林分中树木的死亡率,当林分发展到一定程度时,林分存在自然稀疏现象,林分断面积还与林分密度有关,不会无限制增长。在造林初期(林分郁闭前)和间伐后(间伐强度足够大)的一段时间内,林木间拥有较充足的生长空间,个体树木间的相互作用很小或基本上没有,林分属于等株生长,不发生自然稀疏,即在初始断面积较小的林分,断面积增量变异程度大。随着林分的进一步生长发育,林木间开始为争夺生存空间而展开竞争,且随个体树木的不断增长而竞争加剧,导致林分发生自然稀疏而进入自然生长状态,林分断面积增量只在较小的水平范围内波动。传统建模法模拟的断面积增量,整体呈现出在林分生长状况不好的年份预测值偏高,在生长好的年份,预测值偏低,模拟值总体高于实测值。虽然林分断面积年均增量变异范围减小,但在未来的森林经营中无法确定采取的经营措施。而优化法的模拟值与林分初始断面积呈较强的相关性,且仍有一个动态的调整范围,符合林分预期生长规律。因此,在给定林分平均木大小的情况下,判定模型的好坏,应结合林分平均木(如平均胸径、平均材积)的大小和株数的关系(自然稀疏、立地生境和林分生长发育阶段)综合考虑模型的优劣。

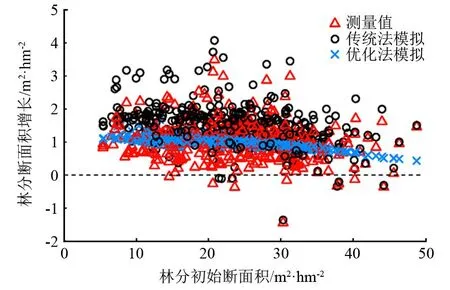
图4 红松人工林林分断面积年平均生长变化

4 结论与讨论

本研究以红松年均生长量为因变量,构建其关于年均单木直径生长模型。在人工林中,假定两个连续测量时间间隔的生长率恒定,以林木直径大小、竞争指标、立地条件等为模型最佳影响因素,模型的决定系数(R2)为0.414 9,均方根误差为0.335 1,表明该模型可以解释林分中单木直径年均增量接近一半的变异,而剩余变异可由气候、现实收集数据的误差引起。林业中存在着诸多不确定性,对黑龙江省红松人工林单木直径生长模型的影响显著。

根据传统建模方法确定模型的影响因素后,基于优化建模法,利用单纯形优化算法求解最小损失函数,优化目标方程的模型参数(a、b、c1、c2)。由于建模数据存在测量间隔期不固定,不能用传统的统计学意义标准去评定模型优劣。使用自举法检验、评估所提出的模型的可信度和精确度。在广泛的测试中,根据以往专家的经验[3,20],将设定为林分断面积权重,并将a值固定,取a=1。对于b和c的取值,进行排列组合和对比分析,当b=0.003且c1=c2=1.5时,模型的偏差和均方根误差最小,表明了构建模型的预测情况与真实值相符。

综合考量统计学与生物学特性,本文对传统建模法与优化建模法在单木直径生长模拟的应用进行了比较。通过设定一定的初始条件模拟单木直径生长,优化法得到的年均直径增量与立地条件具有极强的相关性。由于幼中龄林的林木生长速度较快,并随其成熟度的提升(胸径的增大)而逐渐降低。当胸径超过某一特定值时,直径生长量开始下降。此时,邻近树木逐渐成为竞争因素,林木生长速度变得缓慢,符合林木生长的一般规律。

模拟人工林林分断面积年平均生长变化的结果显示,传统方法使用最小二乘法,模拟人工林林分断面积年平均生长值普遍高于实测值。虽然模拟的变异范围与实际测量值的差距较小,但在未来无法确定树木是否会一直生长或死亡。相比之下,优化法通过控制林分断面积和林分密度的权重,使得变异范围仅在较小的水平范围内波动,并减少了因同号异木等测量误差所造成的估计偏差,从而更符合林木的实际生长规律。因此,当面对不规则的测量间隔时,优化法生成的模型相对于传统模型更能真实地模拟黑龙江省红松人工林的生长情况,适合作为该地区红松人工林单木直径生长的预测模型。