基于多任务学习多目标优化的稀土元素组分含量与浓度多维度软测量

张水平,张奇涵,王 碧

(江西理工大学信息工程学院,江西赣州 341000)

1 引言

稀土因其特有的光、电、磁等性质[1],成为永磁材料、催化材料、储氢材料等材料必须的关键元素,而这些高性能的稀土材料在冶金、化工、航空航天、国防科技等高新技术领域起核心作用,受到国内外科学界的广泛关注[2-5].我国是稀土储量大国,稀土的分离工业规模和产量雄踞世界首位,然而稀土分离工业自动化生产过程中获取组分含量值的方式还基本停留在离线分析的低水平阶段.稀土联动萃取分离工艺流程[6]主要依靠在连续的生产过程中对监测点处的稀土各元素组分含量进行在线检测,通过检测数据来优化控制料液、有机相、洗涤液等物料流量,以此保证分离产品的高纯化.而目前常用的在线检测装置价格高,结构复杂,维护保养困难,因此,探寻具备成本低、维护保养简单、连续检测迅速等优点的稀土元素组分含量软测量[7]方法为提升稀土分离工业自动化水平的关键.

目前,国内有学者使用基于传统机器视觉的机器学习方法[8-10]对稀土元素组分含量进行软测量,虽然该类方法能够独立求解各元素组分含量,并达到萃取过程所需精度,但需要人工筛选并提取稀土混合萃取溶液图像特征,特征提取过程繁琐,相较于深度学习方法[11-12]具有局限性[13];且该类方法未将混合萃取溶液图像中各元素组分含量之间或组分含量与其他相关因素之间联合进行训练及预测,忽略了多个元素组分含量之间或组分含量与其他相关因素之间在稀土混合萃取溶液图像中颜色特征之间的共性,泛化能力不足.深度学习模型能够自动提取图像抽象表征,通过卷积、池化等操作[14]让所提取表征更具泛化能力,而深度学习中的多任务学习方法[15]可以将多个任务联合训练,旨在利用相关任务的训练信号中包含的特定特征来改进泛化能力.与单任务学习相比(每个任务由其单独的网络进行求解),多任务学习具有以下优势:

1)多个特定任务共享一个共享层网络,大大减小内存的占用;

2)避免重复计算共享层网络中的特征,提升模型训练速度;

3)若相关任务共享互补信息,则具有提高模型整体性能的潜力.

从多任务学习方法的角度进行分类,可以分为基于多任务模型结构和基于多任务优化策略两种多任务学习方法[15-16].其中,将多任务模型结构按照处理多图像级分类任务的角度归类,可分为基于硬参数共享和基于软参数共享两种模型结构: 在硬参数共享中,模型参数可分为共享层参数和特定任务层参数,将由一个编码器构成的共享层参数分支到各特定任务层首层,实现参数共享,如Kokkinos[17]提出的Ubernet和Teichmann等[18]提出的Multinet;在软参数共享中,每个特定任务被分配各自的参数集,并由特征共享机制对各特定任务参数集进行交互处理,如Ruder等[19]提出的水闸网络(sluice networks)和Liu等[20]提出的MTAN网络(multi-task attention netwrok).基于多任务优化策略的多任务学习主流方法有Chen等[21]提出的梯度归一化(gradient normalization),旨在平衡多任务网络训练的梯度和速率,鼓励网络以平等的速度学习所有任务,但该方法可能在不同任务的量级不一时导致其中某些任务不能取得良好的解;Kendall等[22]提出的同方差不确定性(uncertainty weighting),使用噪声参数σ作用在损失函数上,用于平衡各特定任务间的权重;上述方法试图通过一些启发式设置损失中的特定权重来解决不同任务间性能相互冲突的问题,不同的是,Désidéri[23]将多任务学习视为一个多目标优化问题,提出了一种多重梯度下降算法(multiple gradient descent algorithm)来解决这个问题,通过寻找不同任务间的Pareto平稳点,使任何特定任务的损失值都在不增加其他损失值的前提下减少;Sener等[24]将在多重梯度下降算法的研究基础上,针对多重梯度下降算法需要对每个任务的梯度进行显示计算比较耗时的问题,提出多目标损失上界,在所有任务中利用基于上界的多重梯度下降算法(multiple gradient descent algorithm-upper bound)找到各任务间的Pareto最优解,通过无需明确特定任务梯度的单个反向计算过程,使训练迭代时间大大减少,并取得了与原方法相近甚至更优的测试性能.基于多任务模型结构和基于多任务优化策略两种多任务学习方法可以交互使用,共同提升模型整体性能.

国内也有学者对多目标优化问题进行研究,张波等[25]在基于多重梯度下降和Frank-Wolfe两个算法上将多目标优化问题分解为多个两目标优化问题,对梯度下降的方向进行梯度更新和线性搜索.周晓君等[26]将多重梯度下降算法用于多车牌识别中,提出基于多目标优化多任务学习的端到端车牌识别方法;赵佳铭等[27]将多重梯度下降算法用于泡沫浮选过程工况识别中,取得了良好的预测效果,但周、赵并没有对训练过程的迭代时间进行统计与比较,无法得知不同算法在不同任务训练迭代过程中的时间性能.

本文受到Sener等的启发,针对稀土萃取在连续的生产过程中对监测点处的稀土各元素组分含量进行在线检测的需求,探索多元素组分含量之间及组分含量与浓度之间的共性,将稀土多个元素组分含量或组分含量与浓度同时训练及预测,并将多个元素组分含量或组分含量与浓度的预测任务转换为一个多任务学习问题,在基于多图像级分类任务的硬参数共享结构上构建多任务学习模型以提升模型泛化力;针对多个任务间可能存在竞争和冲突的问题,将稀土多元素组分含量或组分含量与浓度预测任务视为多目标优化问题,提出基于优化上界的多重梯度下降算法(multiple gradient descent algorithm based on optimal upper bound),找到多个任务间的Pareto最优解,在节省训练时间的同时提升模型预测精度.如图1所示.

图1 稀土组分含量软测量方法Fig.1 Soft measurement method for content of rare earth element components

接下来,本文将在第2节介绍建立在稀土联动萃取分离流程下的稀土多元素组分含量与浓度预测多任务学习模型;第3节详细描述稀土多元素组分含量与浓度预测多目标优化算法;第4节将本文方法与单任务学习、多重梯度下降和其他主流多任务优化方法从以下两个角度在多个预测任务中呈现的性能进行多组对比实验: 1)验证集的损失函数值变化、训练过程单次迭代平均时长;2)10个测试集样本预测值与真实值的误差评价指标值;最后,在第5节对本文进行总结,并对未来工作进行展望.

2 稀土多元素组分含量与浓度预测问题建模

2.1 稀土联动萃取分离流程

稀土联动萃取分离流程中为降低萃取流程所需物料(有机相、洗涤液等)的消耗,使用横纵相连的方式将萃取分离流程中相关分离单元关联,每个单元间彼此提供物料.这种关联方式使稀土分离整体流程中各物料仅需一个输入口,即可设置同时产出所需萃取元素纯产品的各出口.如La/Ce/Pr/Nd这4个稀土元素的联动萃取分离过程(图2),共有6 个分离单元: (LaCePr)/(CePrNd),(LaCe)/(CePr),(CePr)/(PrNd),La/Ce,Ce/Pr,Pr/Nd,6个单元相互横纵相连,通过(LaCePr)/(CePrNd),La/Ce和Pr/Nd 这3个单元分别输入需萃取分离的混合稀土料液、有机相和洗涤液,便可从各元素出口获取4种元素萃取后的纯溶液.

图2 La/Ce/Pr/Nd四元素联动萃取分离流程[6]Fig.2 La/Ce/Pr/Nd four-element linkage extraction separation process[6]

为便于优化整个萃取流程的进料过程,需通过各监测点对萃取液中各元素组分含量的检测值计算出3个进料单元所输入的各料液流量.而由于部分稀土元素(如Pr,Nd)具有独特的离子颜色特征,其萃取溶液具备对光线呈一定反射性和折射性的特点,透光性较好,能在可见光区域呈现颜色特征,满足基于机器视觉技术对稀土元素组分含量软测量的光学成像条件.因此,可在稀土联动萃取分离流程中的待测稀土元素组分含量处设置检测点,采集稀土混合萃取溶液图像,用于模型训练与预测.将稀土元素组分含量软测量数据通过理论公式计算,便可得到各分离单元所需的理论最小萃取量、最小洗涤量及分离单元横纵间联动衔接所需的最优化流量,从而优化控制萃取流程,以此保证分离产品的高纯化.

2.2 基于多任务学习的稀土多元素组分含量与浓度预测模型

为满足稀土联动萃取过程对多元素组分含量检测需求,和探索多元素组分含量之间及组分含量与浓度之间的共性,本文提出一种基于多任务学习的稀土多元素组分含量与浓度预测模型,对所采集稀土混合萃取溶液图像中的稀土多元素组分含量与浓度在共享层网络中同时训练,并设置多个特定任务层网络同时输出组分含量与浓度多个任务的预测结果.多任务学习模型结构如图3所示,该模型中共享层网络由除去末尾全连接层的ResNet18网络构成;每个特定任务层网络头部都与共享层网络相连,实现参数共享,并各设置一个全连接层用于输出特定任务预测值.

图3 基于多任务学习的稀土多元素组分含量与浓度预测模型结构Fig.3 Structure of the multi-task learning-based model for predicting the content and concentration of rare earth multi-element components

该模型建立在基于多图像级分类任务的硬参数共享结构之上,在经过对单稀土元素与浓度同时训练的比较实验中选取了对数据集预测结果拟合效果较好的ResNet18作为共享主干网络.其中ResNet18[28]网络中的残差模块由卷积层、非线性激活函数层、批处理归一化层构成,将批处理归一化(batch normalization)层取代dropout层,对网络隐含层输出进行标准化处理,在保留原有数据的同时使数值更加稳定,并防止了过拟合,网络结构参数如表1所示,其中Conv层实现卷积操作后接批处理归一化操作和ReLU非线性激活函数,第6,10和14层额外进行下采样操作后用于特征短接,特征短接操作使模型可以学习到更深层网络的特征.

表1 ResNet18(除去末尾全连接层)网络结构参数Table 1 ResNet18 (excluding the end fully connected layer)network structure parameters

特别地,为获得单一准确的稀土元素组分含量与浓度预测值,本文将特定任务层网络中正向传播过程中的全连接层输出与Softmax函数[29]相连,利用Softmax函数对特定任务各类别概率的输出与各类别真实值通过线性回归损失函数建立回归模型,再将损失函数值进行反向传播,优化网络参数.线性回归模型中常用的损失函数有L1Loss和L2Loss,分别计算平均绝对误差(mean absolute error,MAE)(式1)和均方误差(mean square error,MSE)(式2),即

其中:yi为模型预测值,为所预测数据点对应任务的真实标签值,n为所预测数据点个数.相较于L1Loss,L2Loss损失函数将误差平方化,会加剧忽略微小的误差.例如,某混合萃取溶液图像样本真实元素组分含量为0.001,其预测值为0.011.虽然误差是真实值的10倍,但数值较小.若使用L2Loss,会进一步增加修改该误差的难度.因此,本文采用L1Loss作为多任务学习模型各任务的损失函数[30].

3 稀土多元素组分含量与浓度预测多目标优化算法

在稀土多元素组分含量与浓度预测多任务学习模型的训练过程中,多个特定任务之间可能会发生冲突,导致共享层网络参数偏向某一个特定任务的情况.本文在受到Sener启发后,尝试将该情况通过多目标优化算法来解决,将多个特定任务共同训练过程视为多目标优化过程,通过找到多个特定任务之间的Pareto 解来平衡各任务之间的竞争,使共享层网络参数不会偏向某个特定任务,从而提高对稀土多元素组分含量与浓度预测的精度.

3.1 多目标优化定义

给定稀土多元素组分含量与浓度预测的多任务学习问题中输入空间X为所采集稀土混合萃取溶液图像,{Yt}t∈[T]为一组稀土混合萃取溶液图像中对应的组分含量和浓度真实值空间,则整个稀土混合萃取溶液图像数据集中的数据点为,其中:T为所需预测的稀土元素组分含量与浓度任务个数,N为稀土混合萃取溶液图像数据点的个数,为第i个数据点对应第t个组分含量或浓度预测任务的真实值标签.再进一步,在多任务学习模型中考虑每个特定任务的参数化假设为ft(x;θsh,θt):X →Yt,其中:θsh为共享层网络参数,θt为特定任务层网络参数.则可将稀土元素组分含量或浓度预测各任务的经验性最小化公式表示为式(3):

其中:ct为特定任务被衡量所计算出的权重;(θsh,θt)为第t个预测任务的经验损失函数,具体可被定义为

式(5)由包含稀土元素组分含量与浓度预测多个任务对应损失函数的向量L组成,目的在于寻求平衡多个任务之间的Pareto解.下面给出在多目标优化中多个任务之间Pareto解的定义:

3.2 基于优化上界的多重梯度下降算法

本文提出一种基于优化上界的多重梯度下降算法,用于寻求稀土元素组分含量与浓度预测多任务学习中的Pareto 最优解,通过多任务学习模型训练中的梯度下降方式完成多目标优化.下面将使用Karush-Kuhn-Tucker(KKT)条件实现多目标优化,该条件也是多目标优化的必要条件.现将基于多任务学习的稀土多元素组分含量与浓度预测模型中共享层网络参数与特定任务层网络参数所需的KKT 条件表示如下:

2)对于任意稀土元素组分含量与浓度预测任务t,=0.满足上述条件的任何解都被称为Pareto平稳点,其中本文模型在完成上述优化条件中所使用损失函数为L1Loss,在第2.2节中被提及.再考虑如下优化问题:

Désidéri等表明: 该优化问题的解为0 时,其解满足KKT条件;否则,该解给定了一个下降方向,优化稀土元素组分含量与浓度所有预测任务.然而,该问题描述的算法需要计算,则需为每个特定任务关联的共享层网络参数进行反向传播,因此,各特定任务的梯度计算需要在T次反向传播得到,再进行正向传播,大大增加了内存和时间的消耗.对此,本文提出基于优化上界的多重梯度下降算法,不同于多重梯度下降算法,该算法优化了目标上界,仅需一遍反向传播就可在正向传播中得到所有特定任务的梯度,节约了内存和时间上的消耗.优化上界需要将共享的表示函数与特定任务的决策函数相结合,可以将假设类约束定义为下式:

其中:g为所有任务共享的表示函数;ft为将该表示作为输入的特定任务函数,若将该表示函数表示为Z=(Z1,···,ZN),其中Zi=g(xi;θsh),则可将上界表示为下式,该式为链式法则的直接结果:

式(9)属于具有线性约束的凸二次问题,求解该优化问题等价于在输入点集的凸包中找到最小范数点.本文先考虑基于两个任务求解的情况,优化问题可被定义为

虽然式(11)只适用于两个任务的求解,但本文将使用Jaggi[31]提出的Frank-Wolfe 算法,将式(10)作为线性搜索的子进程,从而解决两个及以上任务的约束优化问题.Frank-Wolfe 算法流程如图5.所求得α1,···,αT即为基于优化上界的多重梯度下降算法的解,可通过此解优化所有特定任务的下降方向,求得稀土多元素组分含量与浓度预测多目标的Pareto最优.

图5 Frank-Wolfe算法流程Fig.5 Frank-Wolfe algorithm flow

3.3 稀土多元素组分含量与浓度预测多目标优化算法流程

在对于稀土多元素组分含量与浓度预测多个目标进行优化过程中,本文采用基于优化上界的多重梯度下降算法求解各任务在模型训练中的梯度,该算法优化了目标上界,因此,只需经过一遍反向传播,便可在正向传播过程中得到所有特定任务的梯度.此后,再将各特定任务梯度代入Frank-Wolfe算法中求多目标优化解,得到关于稀土多元素组分含量与浓度预测多个任务的Pareto平稳点,实现多目标优化.详细步骤描述如下:

输入:将标准化预处理后的稀土混合萃取溶液图像输入基于多任务学习的稀土多元素组分含量与浓度预测模型,加载图像样本对应真实标签值.初始化共享层网络参数θsh,特定任务层网络参数θt;设置损失函数、最大迭代次数、批大小、优化器和学习率η,在共享层网络中求解多目标优化问题.

输出:在各特定任务层输出稀土元素组分含量或浓度预测值.

步骤1根据式(9)初始化多目标优化上界∇Z(θsh,θt);

步骤2在优化上界下求得每个特定任务的梯度,(t ∈T);

步骤3将所有特定任务的梯度代入Frank-Wolfe算法中,求多目标优化解,得到关于稀土多元素组分含量与浓度预测多个任务的Pareto平稳点α1,···,αT;

步骤4利用α1,···,αT更新共享层网络参数

步骤5更新特定任务层网络参数θt=θt-,(t ∈T),优化所有特定任务的下降方向;

步骤6判断是否达到最大迭代次数,是则进入步骤7,否则返回步骤1;

步骤7根据优化后的共享层网络参数θsh和特定层网络参数θt(t ∈T),对需检测的稀土混合萃取溶液图像中组分含量与浓度进行预测.

4 对比实验及误差分析

为体现本文所提多目标优化算法对稀土多元素组分含量与浓度预测的有效性,本节将在不同预测任务上从以下两个角度,对单任务学习与不同多任务优化方法进行比较: 1)验证集的损失函数值变化、训练过程单次迭代平均时长;2)10个测试集样本预测值与真实值的误差评价指标值.

4.1 制备稀土混合萃取溶液图像数据集及实验环境

本文对基于多目标优化算法的稀土多元素组分含量与浓度预测以Pr(苹果绿色)、Nd(紫红色)两种具备离子颜色特征的稀土萃取溶液为例,进行仿真实验,所使用的Pr/Nd混合萃取溶液经由如下途径获得:

1)原溶液组分含量测量: 于赣南某稀土公司分别购买纯度均为99.9%的1 L1.8275 mol/L PrCL3和1 L 2.063 mol/L NdCL3萃取纯溶液,其稀土浓度和配分均由国家钨与稀土产品质量监督检验中心提供.

2)溶液稀释: 将两种元素原溶液的浓度分别稀释为0.01～0.50 mol/L各11种不同浓度且透光性良好的稀土萃取纯溶液.

3)溶液混合:将两种稀土元素不同浓度的溶液各50 ml分别相互混合,共得到121组不同组分含量与浓度的Pr/Nd混合萃取溶液.

由上述步骤得到Pr/Nd各元素组分含量由1.96%～98.04%变化、浓度由0.005～0.25 mol/L变化的121组稀土混合萃取溶液,并将各组分含量与浓度不同的稀土混合萃取溶液倒入收集皿中密封保存.由于实验室制备的稀土混合萃取溶液具备对光线呈现一定反射性和折射性的实际特点,透光性较好,满足基于机器视觉实验稀土元素组分含量软测量的光学成像条件.同时,在充满稀土混合溶液的容器中形成的“离子颜色特征带”为采用快速、准确且可连续检测的图像识别技术提供可行途径.

实验图像采集时将稀土混合萃取溶液倒入至长宽高为150×5×170 mm的石英容器中,直至溶液填充满容器.并随后将容器置于60 cm摄影棚中.其中,摄影棚中搭建两处LED光源,光源输出电压为24 V,功率为48 W,灯珠流明最大为15000 LM;背景为纯白色;图像采集设备为NIKON D700相机;最终采集图像为4256×2832分辨率的JPG格式图片.

由于拍摄得到的Pr/Nd混合萃取溶液图像(图6)中包含石英容器边缘外非溶液部分及边缘内颜色不均匀部分,因此,将拍摄图像中充满颜色特征的部分进行裁剪,每组溶液图像依照从上至下、从左至右的顺序裁剪10张图片,共获取1210张颜色均匀的稀土混合萃取溶液图像.将稀土混合萃取溶液图像按照Pr,Nd各元素的组分含量与浓度不同归为121个类别,并将每个类别分别标记上Pr,Nd组分含量与浓度的真实标签值,将其中70%划分为训练集,20%划分为验证集,10%划分为预测集,制备成完整数据集,用于基于多任务学习的稀土多元素组分含量与浓度预测模型构建.

图6 部分不同组分含量Pr/Nd混合溶液图像Fig.6 Images of some mixed solutions of Pr/Nd with different component contents

所有模型训练及预测实验都在以下实验环境中实现: 硬件环境为Windows10操作系统,CPU Intel Core i7-12700F(12核),GPU RTX3080(内存为10 G);软件环境为在PyChram上使用的PyTorch深度学习框架.

4.2 对比实验

为验证本文所提基于多目标优化算法的稀土多元素组分含量与浓度预测方法有效性,下面将本文所用多目标优化算法(基于优化上界的多重梯度下降)与单任务学习、多重梯度下降及其他多任务优化主流方法,即梯度归一化、同方差不确定性,从验证集的损失函数值变化、训练过程单次迭代平均时长的角度在以下多个预测任务上进行比较:

1)双预测任务:预测Pr,Nd组分含量(图7);

图7 各方法在Pr,Nd 组分含量双预测任务中验证集损失函数值随迭代次数变化Fig.7 Variation of validation set loss function values with the number of iterations for each method in dualprediction task of Pr and Nd component content

2)三预测任务:预测Pr,Nd组分含量和Pr浓度(图8);

图8 各方法在Pr,Nd 组分含量和Pr浓度三预测任务中验证集损失函数值随迭代次数变化Fig.8 Variation of validation set loss function values with the number of iterations for each method in the threeprediction task of Pr,Nd component content and Pr concentration

3)四预测任务:预测Pr,Nd组分含量和Pr,Nd浓度(图9).

图9 各方法在Pr,Nd 组分含量和Pr,Nd浓度四预测任务中验证集损失函数值随迭代次数变化Fig.9 Variation of validation set loss function values with the number of iterations for each method in the fourprediction task of Pr and Nd component content and Pr and Nd concentration

为保证对比实现的公平性,本文所有多任务优化方法都在基于多任务学习的稀土多元素组分含量与浓度预测模型中实现,且将上述模型与单任务学习模型设置统一的模型主要参数如表2所示,这些主要参数是提升模型整体性能的一般性参数.因此,这对于对比实验中所有优化方法都是公平的.

表2 主要参数设置Table 2 Main parameter settings

由图7-9可以看出本文方法在双、三、四预测任务出中Nd组分含量预测任务的验证集损失函数值最低;在三预测任务中Pr组分含量预测任务及四预测任务中Pr,Nd浓度预测任务中仅次于损失函数值最低的单任务学习;在其他多预测任务中Pr组分、Pr,Nd浓度预测任务的损失函数值均与最低值接近,且优于大部分优化方法.而多重梯度下降在所有预测任务中也呈现出较优的性能,损失函数值普遍低于其他主流多目标优化方法.特别地,梯度归一化在各多预测任务中对Pr,Nd浓度预测的验证集损失值较高,可能是由于Pr,Nd组分含量与浓度两种预测任务的量级不一所导致.

下面将各优化方法在多个任务训练中的单次迭代平均时长进行比较,其中单任务学习训练中的单次迭代平均时长如表3,不同多任务优化方法在多任务学习训练中的单次迭代平均时长如表4.表3中各任务的单次迭代平均时长与表4中各方法同时对所有任务训练不同,是由单任务学习模型对各任务进行独立训练所得.

表3 单任务学习训练中的单次迭代平均时长Table 3 Average time duration of single iteration in single-task learning training

表4 不同多任务优化方法在多个预测任务训练中的单次迭代平均时长Table 4 Average time of single iteration for different multi-task optimization methods in multiple prediction task training

由表3-4可以得知在多任务优化方法中同方差不确定性训练耗时最短,与单任务学习训练时长接近;多重梯度下降耗时最长,且训练时间会随任务数量的增加而增长;本文方法的训练时长仅高于同方差不确定性与单任务学习,优于其他多目标优化方法.

综上可得本文方法在各多预测任务中损失函数值普遍较低,在个别预测任务中损失值仅高于当前任务的最低值,基本优于其他多任务优化方法;本文方法在训练过程中迭代时长与耗时最低的单任务学习和同方差不确定性接近,远远低于多重梯度下降方法,且训练时长不会随着任务数量的增加而增长;由此证明,本文所提基于优化上界的多重梯度下降算法在训练时间上相较多重梯度下降算法的较大优势,在降低训练耗时的同时降低了各预测任务的损失函数值.

4.3 误差分析

为避免基于多任务学习的稀土多元素组分含量与浓度预测模型训练过拟合情况,本小节将对测试集样本进行仿真预测,将预测值与真实值的误差进行比较与分析,判断模型是否在稀土联动萃取过程中对稀土混合萃取图像中组分含量预测误差的最大容错范围内.下面将本文所用多目标优化算法(基于优化上界的多重梯度下降)与单任务学习、多重梯度下降及其他多任务优化主流方法,即: 梯度归一化、同方差不确定性,从10个测试集样本预测值与真实值的误差评价指标值角度在以下多个预测任务上进行比较:

1)双预测任务:预测Pr,Nd组分含量(图10、表5);

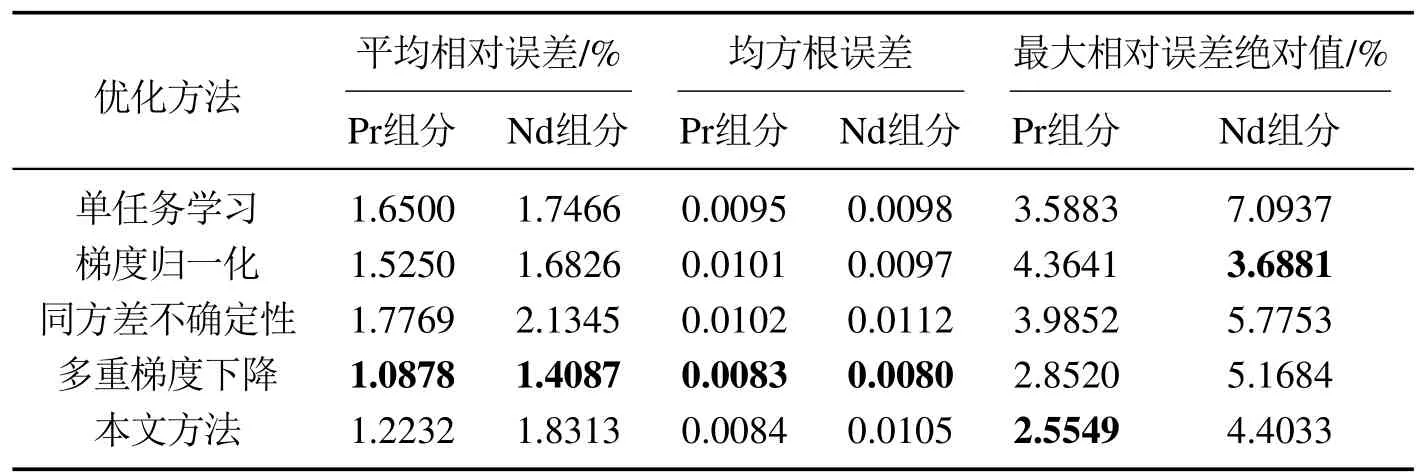
表5 各优化方法在双预测任务下对10个测试集样本预测值与真实值的误差评价指标值Table 5 Error evaluation index values of each optimization method for the predicted and true values of the 10 test set samples under dual-prediction task

图10 各方法在Pr,Nd组分含量双预测任务下对10个预测集样本预测值与真实值相对误差绝对值Fig.10 Absolute values of relative errors between predicted and true values for each method for 10 prediction set samples under dual-prediction task of Pr and Nd component content

2)三预测任务:预测Pr,Nd组分含量和Pr浓度(图11、表6);

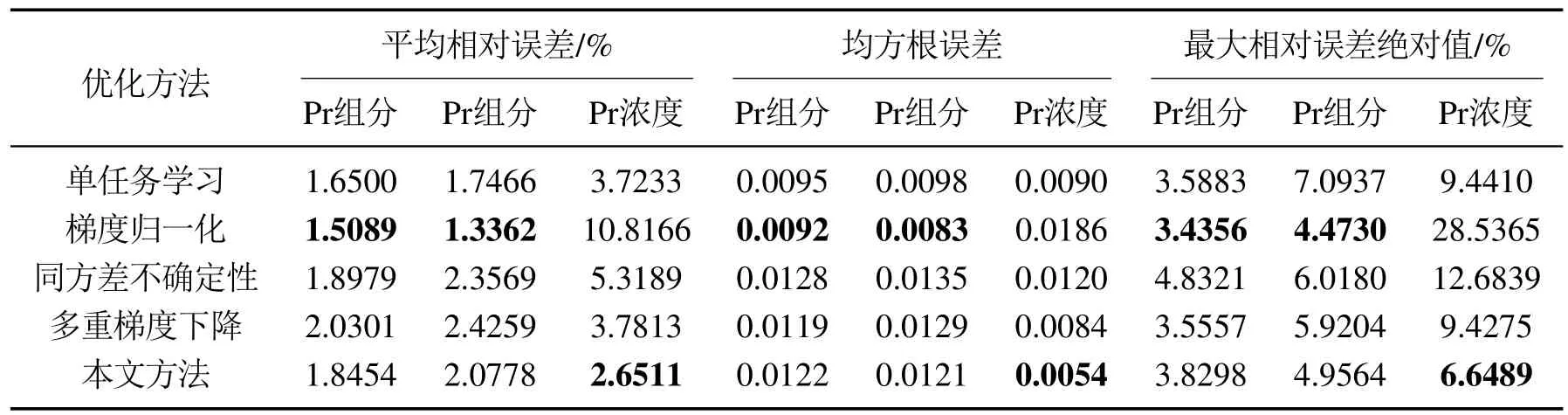
表6 各优化方法在三预测任务下对10个测试集样本预测值与真实值的误差评价指标值Table 6 Error evaluation index values of each optimization method for the predicted and true values of the 10 test set samples under three-prediction task

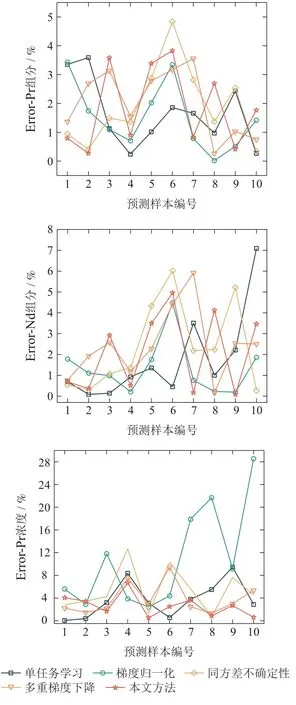
图11 各方法在Pr,Nd组分含量和Pr浓度三预测任务下对10个预测集样本预测值与真实值相对误差绝对值Fig.11 Absolute values of relative errors between predicted and true values for each method for 10 prediction set samples under the three-prediction task of Pr,Nd component content and Pr concentration

3)四预测任务:预测Pr,Nd组分含量和Pr,Nd浓度(图12、表7).

表7 各优化方法在四预测任务下对10个测试集样本预测值与真实值的误差评价指标值Table 7 Error evaluation index values of each optimization method for the predicted and true values of the 10 test set samples under four-prediction task

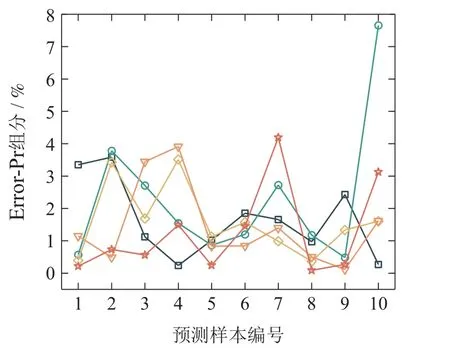
图12 各方法在Pr,Nd组分含量和Pr,Nd浓度四预测任务下对10个预测集样本预测值与真实值相对误差绝对值Fig.12 Absolute values of relative errors between predicted and true values of samples from 10 prediction sets under four-prediction task of Pr and Nd component content and Pr and Nd concentration by each method

由图10-12可以从纵坐标明显看出各优化方法在对Pr,Nd组分含量预测任务中相对误差相差不大,但在对Pr,Nd浓度预测任务中相对误差较大,由其是梯度归一化的误差波动幅度较大,该现象与梯度归一化在验证集损失函数值较高表现一致.

由表5-7可以看出如下6点:

1)在双预测任务中,将本文方法与单任务学习比较: 本文方法在Pr组分预测任务的平均相对误差、均方根误差、最大相对误差绝对值与Nd组分最大相对误差绝对值都低于单任务学习,在Nd组分预测任务的平均相对误差、均方根误差与单任务学习接近,整体优于单任务学习;与其他多任务优化方法比较: 本文方法在Pr组分含量预测任务的平均相对误差、均方根误差仅次于多重梯度下降,Pr组分预测任务的最大相对误差值为所有优化方法中最低,Nd 组分预测任务的最大相对误差值仅低于梯度归一化.因此,本文方法在双预测任务中整体性能仅次于多重梯度下降.

2)在三预测任务中,本文方法在Pr浓度预测任务的平均相对误差、均方根误差、最大相对误差绝对值均为所有优化方法中最低.将本文方法与单任务学习比较: 除上述最低外其他误差评价指标均高于单任务学习,整体次于单任务学习;将本文方法与其他多任务优化方法比较: 本文方法在除上述最低外,其余误差评价指标整体仅次于梯度归一化,优于其他多任务优化方法,但梯度归一化在Pr 浓度预测中误差较高,不适用于在量级不一的任务中进行训练及预测.因此,本文方法在三预测任务中整体性能仅次于单任务学习.

3)在四预测任务中,本文方法在Nd组分、Nd浓度预测任务的平均相对误差、均方根误差、最大相对误差绝对值与Pr组分预测任务中的平均相对误差均低于其他优化方法,整体性能较优;将文本方法与单任务学习比较: 除上述最低外,其余误差评价指标值均高于单任务学习,但整体性能优于单任务学习;与其他多任务优化方法比较,除上述最低外,在Pr浓度预测任务的平均相对误差、均方根误差均低于其他优化方法.因此,在四预测任务中,本文方法整体性能优于其他优化方法.

4)将单任务学习与多任务优化方法比较: 单任务学习仅在四预测任务中Pr浓度预测任务的各项性能评价指标最低,其余指标在所有预测任务中均高于多任务优化方法的最低值,说明多任务学习相较于单任务学习,能找到组分与浓度各任务中的相关性,共同提升模型整体性能.

5)将多个预测任务之间的结果进行比较,首先,将双、三、四预测任务中的Pr,Nd组分预测任务误差评价指标值进行比较,可以发现三预测任务中的各Pr,Nd组分预测任务误差均高于双、四预测任务,说明只有将各元素组分同时训练及预测或将各元素组分与浓度同时训练及预测对提高组分含量预测精度有效;其次,将三、四预测任务中的Pr浓度预测任务进行比较,可以发现三预测任务中Pr浓度预测任务的误差评价指标值普遍低于四预测任务,因此,将元素组分与浓度两种任务同时训练及预测只能提升组分预测的精度,并不能提升浓度预测精度;最后,将双、四预测任务中的组分预测任务进行比较,可以发现双预测任务的各误差评价指标比四预测任务稍低,但基本接近,说明将组分任务同时训练及预测与将组分与浓度两种任务同时训练及预测对组分预测精度的提升不明显.

6)将本文方法在各多预测任务的误差评价指标值中进行比较,可以得出与第5点一致的结论,而本文方法在双、三、四中的Pr,Nd 组分最大相对误差绝对值依次为,双任务: 2.5549%,4.4033%;三任务:3.8298%,4.9564%;四任务:4.1913%,3.4028%,均满足稀土萃取生产中对组分含量检测最大相对误差在±5%[9]以内的要求.

5 结论

针对稀土联动萃取流程对多稀土元素组分含量预测的需求,以及探索多元素组分含量间及组分含量与浓度间的共性,本文首先提出基于多任务学习的稀土多元素组分含量与浓度预测模型用于多个任务的同时训练及预测;接着,为防止多个任务在模型中竞争与冲突的问题,提出一种稀土多元素组分含量与浓度预测多目标优化算法-基于优化上界的多重梯度下降算法,通过此算法搜索模型中各任务间的Pareto最优,提高预测精度;最后,从验证集的损失函数值变化趋势、训练过程单次迭代平均时长与各优化方法在10个测试集样本预测值与真实值的误差评价指标,这两个角度在多个预测任务中呈现出的性能进行多组对比实验,得到以下结论:

1)单任务学习在验证集损失函数值上较低,但是在仿真验证中并未得到良好的效果,出现了过拟合现象,而多任务学习通过多个任务的联合训练,在仿真实验中取得了优异的效果,证明多任务学习能够找到多个任务之间的共性,提升模型整体泛化力和鲁棒性;

2)本文方法在训练过程中单次迭代平均时长与耗时最短的单任务学习和同方差不确定性接近,远远低于多重梯度下降方法,且训练时长不会随着任务数量的增加而增长,在多任务优化方法中具有训练耗时短的优势,弥补了双预测任务中整体误差高于多重梯度下降的不足;而本文方法在三预测任务中整体性能仅次于单任务学习;在四预测任务中整体性能优于其他优化方法.因此,本文方法相较其他优化方法,在训练时长和预测精度上整体占优,更适用于稀土多元素组分含量与浓度预测;

3)将稀土元素组分含量与浓度两种任务联合训练只能提升组分含量的预测精度,并不能明显提升浓度的预测精度;而四预测任务(Pr,Nd组分含量,Pr,Nd浓度预测)仅比双预测任务(Pr,Nd 组分含量预测)的组分含量预测精度稍高,不能明显提升组分含量的预测精度.由此说明组分含量与浓度两种任务共性不足,联合训练效果欠佳;而多种元素的组分含量之间具有良好的共性,其联合训练能够共同提升各元素组分含量的预测精度;

4)本文方法在各预测任务中对组分含量预测的最大相对误差均在稀土萃取生产中对组分含量检测最大相对误差在±5%要求以内,预测时间成本在3 s以内,能满足稀土联动萃取过程中对多元素组分含量在线软测量的精确性与实时性,为稀土元素组分含量软测量方法提供了新思路.