高寒高海拔地区路面性能预测

胡金辉 贡觉卓玛 王辛岩

西藏大学 西藏 拉萨 850011

作为世界上高原分布最广泛的国家，有着被誉为“世界屋脊”之称的青藏高原[1]。青藏高原的平均海拔在4750m，有着世界上面积最广、厚度最大、温度最低的多年冻土区。青藏高原位置环境条件特殊，对道路工作的环境影响十分恶劣，在此建成的公路在通车后两年甚至更短的时间就会出现诸多病害[2]。在高原上的道路养护原则就是以预防为主，对道路的病害进行防治，控制道路病害范围扩大和病害程度加剧。

对道路的养护就类似于打疫苗一样，在患病之前进行干预，以此来降低患病的风险，预防性的道路养护，一定程度上能延缓寿命或减少道路病害，不少学者都对此都进行了研究。缠艳萍[3]，针对青藏高原独特的环境，研究出了一种抗光氧老化性能较好的雾封层道路路面养护材料。张卫亮[4]，对青藏高原道路路面主要病害提出采用热拌乳化沥青冷补材料的新方法。唐靖武等人[5]，通过对拉萨市的道路病害调研，提出可采用抗老化性能优化的沥青材料。对于灰色—马尔可夫预测模型的研究，张嘉琦[6]，对比多种模型的不同结果，认为将灰色预测和马尔科夫法结合会减小预测误差。刘喆等学者[7]，构建了灰色—马尔可夫模型，其结果比残差修正的灰色模型的预测结果更接近于实际值，拟合精度更高，更符合实际要求。

由于当前的研究主要集中在低海拔和高等级的城市道路，对高海拔地区道路研究不足，本文将针对高海拔高寒条件下某青藏公路在未来五年的路面使用性能进行预测，利用MTLAB软件构建三种GM（1,1）模型，并进行对比分析，对比出合适的模型再与马尔可夫理论结合，利用马尔可夫理论对灰色预测结果进行修正。最后根据预测结果，提出符合实际情况的养护策略，为青藏高原上的道路养护工作提供借鉴。

1 综合预测模型的构建

灰色—马尔可夫预测模型是将灰色系统理论和马尔可夫理论相结合的预测模型，通过对历史数据的分析，预测未来的发展趋势[8]。将两者结合起来，用灰色预测对道路路面使用性能进行预测，再使用马尔可夫理论对其远期的预测结果进行修正，获得数据未来变化规律，从而获得道路路面使用性能衰减的规律[9]。

1.1 灰色预测模型原理

步骤1：进行准指数规律检验，定义级比为累加数列相邻前两项的比值如果对于且则该数据符合准指数规律检验，可进行后续操作。

指标1：光滑比小于0.5的数据占比要大于60%；

指标2：除去前两期外，光滑比小于0.5的数据占比要大于90%。

步骤3：将原始数据累加来弱化其波动性和随机性，进而得到新的数据：

其中，是之前的t项数据累加之和。

步骤4：在新生成的数据基础上，使用线性动态方程对其进行拟合，其白化方程可表示为：

此方程的专属解为

其中的p、q的值可以用最小二乘法求得，如下所示：

其中

步骤5：对预测结果进行精度检验，预测模型的残差用表示，级比用表示，如下所示：

表1 检验标准

1.2 马尔可夫模型预测原理

(1)马尔可夫预测模型是通过对事件发生的概率进行预测的，而在所有预测的数据中都是处于不同的状态，故而需要将其按照不同的状态进行划分，划分是主要依据于GM（1,1）模型原始数据与预测值之间的比值：基于该值的大小情况对其状态进行划分：分别为其比值的上下限，马尔可夫预测模型的关键在于状态转移概率矩阵，但是状态转移是有上下限的。

(2)建立状态转移概率矩阵：

(3)计算预测值

取状态上下限的中间值对GM（1,1）模型所得预测值进行修正：

2 实例分析

本研究以西藏自治区某城市道路路段路面使用性能衰变情况为研究对象，该公路为三级公路，路面材料为级配碎石基层沥青路面，处于高海拔高寒冻土地区，是西藏自治区内通往可可西里核心区最便捷的道路。对该地区的道路面对的问题，针对其养护问题，本研究提出灰色—马尔科夫预测模型对道路的路面使用性能进行预测分析，并对预测结果提出合理的养护策略。

2.1 灰色系统预测计算

本研究的道路路面使用性能原始数据样本空间数量小于10期，且原始数据都是非负的离散数据，利用微分方程来挖掘出数据之间的联系，故而灰色预测适合来求解该问题。

对该道路进行实地勘察可估计得其道路路面使用性能（PCI）的值，将其作为原始数据：

累加生成数列：

进行准指数规律检验如表2所示。

表2 准指数规律检验

准指数规律检验：

指标1：光滑比小于0.5的数据占比为75%；

指标2：除去前两个时期之外，光滑比小于0.5的数据占比为100%。

故而，数据通过了准指数规律检验，可以使用灰色系统预测。

将数据带入MATLAB程序中运用GM（1,1）模型建立，用GM（1,1）模型、新信息GM（1,1）模型、新陈代谢GM（1,1）模型对此数据进行预测，将前三期的数据定为训练组，用以训练所用模型，后两期数据定为试验组，将所用模型对该两组进行预测，测试其预测准确率，最后比较其残差平方和（SSE）的大小，预测结果如表3所示。

表3 不同模型的误差平方和

对比分析可得，新陈代谢GM（1,1）模型的误差平方和值最小，故而选择新陈代谢GM（1,1）模型对数据进行后续的预测，预测结果如表4所示。

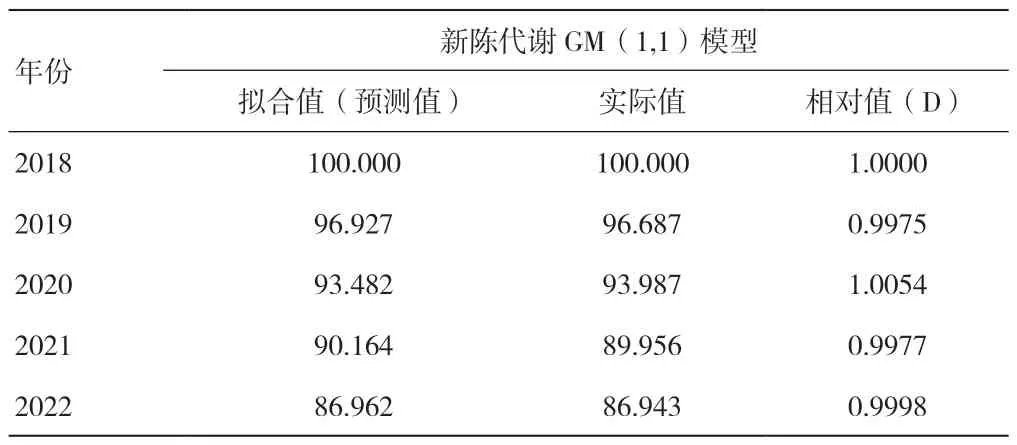
表4 新陈代谢GM（1,1）模型预测值

对于原始数据拟合的评价结果如下：

残差检验的结果表明该模型对原数据的拟合程度非常不错；

级比偏差检验的结果表明该模型对原数据的拟合程度非常不错。

2.2 利用马尔可夫理论进行修正

根据GM（1,1）模型预测结果的相对值，将数据划分为两个状态如表5所示，分别为分别以0.994，0.999，1.006为阈值。

表5 相对值划分

根据马尔可夫转台转移概率矩阵的计算方法，计算该状态的转移概率矩阵如下所示：

进而，利用马尔可夫原理对灰色预测的数据进行修正，结果如表6所示。

表6 马尔可夫修正结果

2.3 灰色—马尔可夫预测结果

用灰色—马尔可夫模型对该道路未来五年的路面使用性能进行预测，预测结果如表7所示。

表7 未来五年预测结果

路面的养护方案是基于路面实际破损状况来拟定的，不同的养护方式都有各自的临界路面破坏状态，以下根据美国路面管理系统所采用的路面使用性能指数（PCI）和路况评级关系来对上述所预测的值进行划分，如表8所示。

表8 路面使用状况（PCI）与评级

按照本次测试路段的路面使用状况（PCI）的实测值以及表7的预测值，以及表8给出的路面使用状况（PCI）与评级标准，并结合此次试验道路所处的高寒高海拔公路养护资料等综合得出建议，在寿命周期预测的十五年之内，本研究中的道路中修的周期为每八年一次，而且只需要进行中修就能够满足路面的使用性能。

3 结语

本研究结合高寒高海拔上的特殊地理环境和道路路面的养护工作，对高寒高海拔某地区道路的路面使用状况（PCI）用灰色—马尔可夫模型对其衰变情况进行规律预测，在寿命预测周期十五年范围内，该道路路面材料为级配碎石基层沥青路面得出了试验道路的养护工作每八年进行一次中修即可，如若在某年存在大修的工程，就不必再进行中修。

由于高原上环境的特殊性，其公路养护工作及其严峻，该预测方法为高原的道路养护提供了借鉴。但是，高原上的道路病害情况易受气候的影响，公路养护还需要结合当地的公路使用情况、车辆荷载和道路病害现状综合起来统筹规划，只有科学的养护规划，才能真正的最好公路病害的防止工作。