Rogue waves for the (2+1)-dimensional Myrzakulov–Lakshmanan-IV equation on a periodic background

Xiao-Hui Wang and Zhaqilao

1 College of Mathematics Science,Inner Mongolia Normal University,Hohhot 010022,China

2 Laboratory of Infinite-dimensional Hamiltonian System and Its algorithm Application,Hohhot 010022,China

3 Center for Applied Mathematical Science,Inner Mongolia,Hohhot 010022,China

Abstract In this paper,the rogue wave solutions of the (2+1)-dimensional Myrzakulov–Lakshmanan(ML)-IV equation,which is described by five component nonlinear evolution equations,are studied on a periodic background.By using the Jacobian elliptic function expansion method,the Darboux transformation (DT) method and the nonlinearization of the Lax pair,two kinds of rogue wave solutions which are expressed by Jacobian elliptic functions dn and cn,are obtained.The relationship between these five kinds of potential is summarized systematically.Firstly,the periodic rogue wave solution of one potential is obtained,and then the periodic rogue wave solutions of the other four potentials are obtained directly.The solutions we find present the dynamic phenomena of higher-order nonlinear wave equations.

Keywords: rogue waves on a periodic background,(2+1)-dimensional Myrzakulov–Lakshmanan-IV equation,Darboux transformation,Jacobian elliptic function

1.Introduction

A rogue wave is a strange wave with an extremely large amplitude.It usually occurs in the ocean,coming from nowhere and disappearing without a trace,which can lead to a deadly disaster[1,2].However,there is currently no effective method available to accurately forecast the rogue waves in advance.Therefore,the study of rogue waves is necessary and relevant [3,4].In recent years,more and more attention has been paid to rogue periodic waves generated on the background of Jacobian elliptic periodic waves.In 2018,Chen and Pelinovsky established a method for calculating such rogue periodic waves based on the precise description of the periodic and aperiodicial characteristic functions of the the Ablowitz–Kaup–Newell–Segur (AKNS) spectrum.They combined the method of the nonlinearization of the Lax pair with the Darboux transformation to obtain the rogue periodic wave of the focused nonlinear Schrödinger (NLS) equation[5].Then,rogue wave on a periodic background of the modified Korteweg–de Vries (mKdV) equation [6,7],Ito equation [8],fourth-,fifth-,sixth-,seven-order NLS equation[9–12],the sine-Gordon equation [13],and the Hirota equation [14,15] has been studied similarly.In recent years,the same method has been used to study the (2+1) dimensional nonlinear evolution equation [16,17].

As a model of nonlinear partial differential equations,integrable spin systems are important because of their applicability in many scientific fields.They give rise to important applications in applied magnetism [18] and nanophysics [19].The Landau–Lifshitz–Gilbert (LLG) equation[20] in ferromagnetism and Landau–Lifshitz–Gilbert–Slonczewski (LLGS) equation [19] in spin transfer nanomagnetic multilayers are some of the fundamental equations that play a crucial role in understanding various physical properties of magnetic materials and the development of new technological innovations,like microwave generation using the spin transfer effect [21].The continuum limit of the Heisenberg ferromagnetic spin system and its various generalizations give rise to some of the important integrable spin systems in (1+1)dimensions [22,23].They are also intimately related to the nonlinear Schrödinger family of equations through geometrical (or Lakshmanan equivalence or L-equivalence) and gauge equivalence concepts and these systems often admit magnetic soliton solutions.Moreover,the system is closely related to the well-known NLS equation[24].R Myrzakulov,G K Mamyrbekova and others mainly presented convincing studies of the integral (2+1)-dimensional spin model with self-compatibility potential,namely the ML-II,III,and IV equations [25].In this paper,we study the (2+1)-dimensional ML-IV equation,which has the following form:

whereZ=.

The gauge equivalent counterpart of the ML-IV equation takes the form:

where ‘*’ is the complex conjugate,q(x,y,t),p(x,y,t) are complex functions,v(x,y,t),w(x,y,t),η(x,y,t) are real functions,and ω,∊1,∊2are arbitrary constants.Here,τ=±1 represents two different cases of the ML-IV equation.To be precise,τ=1 and τ=–1 mean that the ML-IV equation has an attractive interaction and repulsive interaction respectively.

In [26],the soliton,breather,rogue wave and DT of (2)were researched.Its modulational instability and mixed solution have also been studied [27].Based on (2),which has a variety of parameter selections,these parameters will produce abundant reduction results.When ∊1=0,∊2=1,p=0,η=0,(2) can reduce to the (2+1)-dimensional complex mKdV equation,in which multi-soliton and periodic solutions have been studied via DT[28,29].The rogue periodic waves of the (2+1)-dimensional complex mKdV equation have also been studied [30].If we choose ∊1=1,∊2=0,p=0,η=0,(2)can reduce to the(2+1)-dimensional NLS equation,its DT,soliton,breather,abundant rogue wave shapes,rational and semi-rational solutions and the dynamic process have been investigated[31–33].In[34],the author especially studied the lump and rogue wave solutions based on a periodic background in a Heisenberg ferromagnetic spin chain.As far as we know,there are few studies on the rogue periodic waves of (2+1)-dimensional ML-IV equation.Thus,this will become the main content of our next research.

In this work,we mainly construct the rogue periodic wave solutions for the (2+1)-dimensional ML-IV equation.In section 2,we give the Lax pairs and classical Darboux transformation of (2).In section 3,we give the periodic traveling wave solutions.In section 4,we describe the eigenvalues based on the results of the nonlinearization of the Lax pair.In section 5,we obtain the periodic and non-periodic wave solutions of(2).In section 6,the expression and figures of the rogue periodic wave solutions are given.In section 7,we give some conclusions.

2.The Lax pair and Darboux transformation

(2) has the Lax pair in the form

where λ is a complex spectral parameter.The zero curvature equationUt-Vx-(2∊1λ+4∊2λ2)Uy+[U,V]=0 gives rise to (2).According to [26],the elementary Darboux transformation of (2) can be redefined as

3.Two families of periodic solutions

In order to construct the periodic wave solutions of (2),we suppose the complex periodic wave solutions in the form

where ξ=x-c1y-c2t,ζ=x-b1y-b2t,Q(ξ) is a real periodic function andc1,c2,b1,b2are real constants.It is also easy to find that |q|2=qq*=Q2.

Substituting equations (6) into (2) yields a fifth-order nonlinear ordinary differential equation,in which it is difficult to obtain exact solutions.However,the fifth-order nonlinear ordinary differential equation can be simplified to a first-order nonlinear ordinary differential equation by means of the Jacobian elliptic function expansion approach[35].Then,we finally obtain two families of periodic solutions for(2),which are expressed by Jacobian elliptic functions dn and cn as

where ξ=x-c1y-c2t,k∊(0,1)is the elliptic modulus and equations (7)–(8) satisfy the following two elliptic equation:

wherea0anda1are two real constants.As for the dn-function solution,we takea0=2-k2anda1=k2-1.As for the cnfunction solution,we takea0=2k2-1 anda1=k2(1-k2)on the other side.

4.Squared periodic eigenfunctions of Lax pair

In this section,we introduce the Bargmann constraint[36–38]to make the nonlinearization of the Lax pair (3)–(4).Considering the following Bargmann constraint

whereφ=is a non-zero solution of the Lax pair(3)–(4) with λ=λ1.

Substituting (10) into (3),we obtain a finite-dimensional Hamiltonian system as

For the Hamiltonian system (11) and (12),there are two conserved integrals

whereH0,H1is constant with respect toxandH=H1-.

Considering equations (10) and (13) together,we have

Some other constraints with λ1=α+iβ can be referred from [4]

where α,β are the real and imaginary parts of λ1.Substituting(6)into(16),it is easy to notice that the left-hand side of(16)is 2iQ2,which yields

Substituting (6) into (17)–(18)and comparing them with the two equations in (9),we have

According to the second equation in (19),we have two cases asβ=orβ≠withH1=4β2-3β+.

Case 1.Whenβ=,that isH0=0,then the expression ofa0,a1can be simplified as

As a result ofa1=<0,we discuss the dn-periodic backgroundQ(ξ)=dn (ξ;k).Based on the above analysis,we haveH1=,α2=.TheH1and λ1=α+iβ are expressed by the elliptic modulusk.That is to say,the eigenvalues of the Lax pair have two pairs of complex values λ1±in the right half-plane and-λ1±in the left half-plane.

Case 2.Whenβ≠,then the expression ofa0,a1will become

As a result ofa1>0,we discussQ(ξ)=kcn (ξ;k).The eigenvalue for λ1in the first quadrant can be given as

and there also exist some other eigenvalues with -λ1,in other quadrants.

5.Periodic and non-periodic solutions of the Lax pair

In this section,we firstly give the definitions of the squared periodic eigenfunctions of the Lax pair (3)–(4) and obtain various relationships between the solutions of the Lax pair(3)–(4)on the background of the Jacobian elliptic functions dn and cn respectively.Then,we introduce a function θ(x,y,t) to establish a connection between periodic solutions and nonperiodic solutions for the Lax pair(3)–(4).Therefore,the chief aim of this section is to find out the expression of θ(x,y,t).

Based on (10),(13) and (15),we have

Due toq(x,y,t)=Q(ξ)eiζ,we take

Substituting (6) and (26) into (25) yields

According to (28) with λ1=λ±,we findare real.Also,because=Q=dn (ξ;k)>0,we finally determine that Φ1and Φ2are real so that the first equation of(29) can be rewritten as

As for the cn-function solutionQ(ξ)=kcn (ξ;k)in(20),we already know thatH0=2β-1,H1=4β2-3β+,H=β(2β-1) and.Therefore,equation (28) can be rewritten as

Equations (12) and (14) yield (∣φ1∣2+∣φ2∣2)2=1-k2+∣q∣2.If we consider the positive square root,we have

so we obtain

We choose roots of the relation

According to (32) and (35),we have

According to (24) and (27),we have

Here,we introduce a function θ(x,y,t).Let us make an assumption thatis the periodic solution of the Lax pair (3)–(4) with λ=λ1,andis the second linearly independent solution of the Lax pair (3)–(4) with the same λ=λ1,where ψ1and ψ2are non-periodic solutions and have the following forms

where θ=θ(x,y,t) is a function to be determined.

Using (38) and (3) yields

Using (26),we rewrite (39) as

Substituting (28) into (40) yields

Integrating (41) yields

where θ0(y,t) is an undetermined integral constant ofy,t.

If we substitute(38)into(4),a rather complex expression for θtwill be derived,which is difficult to deal with.By using the Jacobian elliptic function expansion method to simplify,we get

In order to determine the form of θ,we suppose that

Based on the equations (43)–(46),the differential equation about χ becomes

where χ can be rewritten as

where

We finally arrive at the expression of θ(x,y,t) as

6.Rogue waves on the periodic background

Proposition.The periodic rogue wave solutions ofw(x,y,t),v(x,y,t),p(x,y,t),η(x,y,t)are related to the periodic rogue wave solutions ofq(x,y,t) as follows

6.1.Rogue waves on the dn-periodic background

In order to construct the rogue waves of(2)on the dn-periodic background,we apply one-fold Darboux transformation (5)to the Jacobian elliptic function dn,take the seed solution asq=Q(ξ)eiζand choose the eigenvalueλ1=λ+=in (35).Substituting=defined by (22) and (38) into the one-fold DT formula,we construct the rogue wave solution of equation(2)on the dn-periodic background as

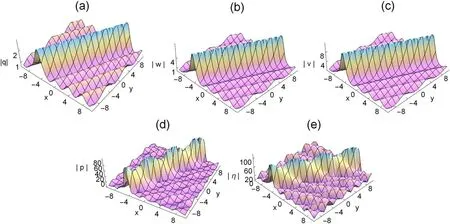
Figure 1. Three-dimensional plots of the rogue waves on the dn-periodic background,with k=0.5,∊1=1,∊2=1,ω=2, b1=1,c1=,b2=3,c2=2,τ=1 t=0.

with

where Δ0is defined in (44).

According to the relation in the proposition,the rogue dn-periodic waves of the other four potentials can be obtained.

It is evident from figure 1 that the periodic rogue waves of the (2+1) dimensional ML-IV equation are mainly linear rogue waves.Figures 1 and 3 illustrate the rogue dn-periodic waves fork=0.5 andk=0.99,we find that the amplitude of rogue periodic waves reaches a maximum value at their origin.The corresponding two dimensional plots are presented in figures 2 and 4.In these figures,with the increase of the elliptic modulusk,the amplitude of the rogue periodic waves also increases.Moreover,we can see from figures 2 and 4 that the amplitudes of the rogue periodic waves of the five potentials are different,η(x,y,t)is the largest,q(x,y,t)is the smallest,and the frequencies of the periodic background waves ofq(x,y,t),w(x,y,t),v(x,y,t),p(x,y,t),and η(x,y,t) are also different.When the range of fixedtis between 0 and 10,it can be observed that theq(x,y,t),w(x,y,t),v(x,y,t)periodic wave speed and the shape of the periodic wave remain consistent,while thep(x,y,t),η(x,y,t)periodic background wave shows an irregular periodic amplitude.It has the same property whenkis equal to 0.99.When the values ofc1,c2,b1andb2are changed,the frequency of the periodic background wave will change accordingly.

6.2.Rogue waves on the cn-periodic background

In order to construct the rogue waves of(2)on the cn-periodic background,we apply the one-fold Darboux transformation(5)to the Jacobian elliptic function cn,take the seed solution asq=Q(ξ)ei(ζ)and choose the complex eigenvalueλ1=λ±=in (24).Substituting=defined by (38) into (5) and using(41),(43) and (45),we obtain the rogue wave solution of (2)on the cn-periodic background as

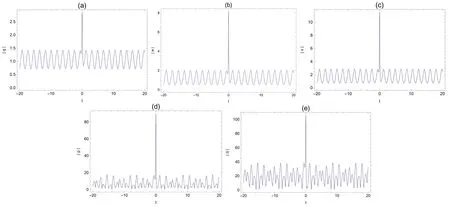
Figure 2. Transverse plots of the rogue waves on the dn-periodic background,with k=0.5,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t-axis.

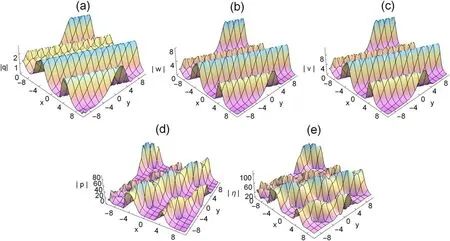
Figure 3. Three-dimensional plots of the rogue waves on the dn-periodic background,with k=0.99,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t=0.

Figure 4. Transverse plots of the rogue waves on the dn-periodic background,with k=0.99,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t-axis.

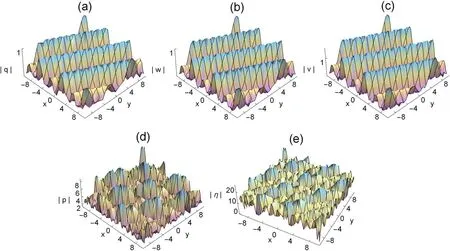
Figure 5. Three-dimensional plots of the rogue waves on the cn-periodic background,with k=0.5,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t=0.

with

Figure 6. Transverse plots of the rogue waves on the cn-periodic background,with k=0.5,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t-axis.

Figure 7. Three-dimensional plots of the rogue waves on the cn-periodic background,with k=0.99,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1,t=0.

Figures 5 and 7 illustrate the rogue cn-periodic waves fork=0.5 andk=0.99,we find that the amplitude of the rogue periodic waves reach a maximum value at their origin.The corresponding two dimensional plots are presented in figures 6 and 8.In these figures,with the increase of the elliptic modulusk,the amplitude of the rogue periodic wave also increases.Moreover,we can see from figures 6 and 8 that the amplitudes of the rogue periodic waves of the five potentials are different,η(x,y,t) is the largest,q(x,y,t) is the smallest,and the frequencies of the periodic background waves ofq(x,y,t),w(x,y,t),v(x,y,t),p(x,y,t),and η(x,y,t)are also different.When the range of fixedtis between 0 and 10,it can be observed that theq(x,y,t),w(x,y,t),v(x,y,t) periodic wave speed and the shape of the periodic wave remain consistent,while thep(x,y,t),η(x,y,t) periodic background wave shows an irregular periodic amplitude.Different from the dn-background,whenkis equal to 0.5,the amplitude ofp(x,y,t),η(x,y,t)periodic background wave changes significantly.It has the same property whenkis equal to 0.99.When the values ofc1,c2,b1andb2are changed,the frequency of the periodic background wave will change accordingly.

Figure 8. Transverse plot of the rogue waves on the cn-periodic background,with k=0.99,∊1=1,∊2=1,ω=2,b1=1,c1=,b2=3,c2=2,τ=1 t-axis.

7.Conclusion

In this paper,we constructed rogue wave solutions of(2+1)-dimensional ML-IV equation on the elliptic dn-and cn-periodic background.Using the nonlinearization of Lax pair,we have determined the eigenvalues and squared eigenfunctions that correspond to the elliptic traveling wave solutions of(2+1)-dimensional ML-IV equation.After that,we gave the non-periodic solution of the Lax pair under the same eigenvalue.Compared with the existing research,the periodic rogue wave solutions studied in this paper mainly present the state of linear rogue waves.Firstly,under the premise of the same elliptic mode,the periodic rogue wave solution with different potential is analyzed.When the elliptic modulus changes,the linear solitons will also change.These results have considerable significance when exploring other highdimensional generalized integrable equations in the future.However,all the research results are still under the framework of AKNS system.In the future,we expect to apply the method in this paper to other spectral problems and expand the periodic background to other Jacobian elliptic functions.We hope that our research results can provide some implications for rogue wave phenomena in the field of nonlinear physics.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No.12 361 052),the Natural Science Foundation of Inner Mongolia Autonomous Region,China (Grant Nos.2020LH01010,2022ZD05),the Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (Grant No.NMGIRT2414),the Fundamental Research Funds for the Inner Mongolia Normal University,China (Grant No.2022JBTD007),and the Key Laboratory of Infinite-dimensional Hamiltonian System and Its Algorithm Application (Inner Mongolia Normal University),and the Ministry of Education (Grant Nos.2023KFZR01,2023KFZR02).

X H Wang:Methodology,writing—original draft,software,visualization,data curation.Zhaqilao:Conceptualization,formal analysis,writing—review and editing,supervision,project administration,funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.