基于改进经验模态分解的直线电机伺服系统迭代学习控制
刘思诺 武志涛
基于改进经验模态分解的直线电机伺服系统迭代学习控制
刘思诺 武志涛
(辽宁科技大学电子与信息工程学院,辽宁 鞍山 114051)
针对直线电机伺服系统迭代学习过程中因误差积累效应引起的收敛速度慢和跟踪精度差的问题,提出一种基于改进经验模态分解的控制策略。首先,设计一种具有自适应性调节特点的迭代学习位置控制器。然后,提出一种基于三角极值波延拓与互补集合经验模态分解的改进算法,该算法可将各次迭代的跟踪误差进行分解,筛选并剔除影响误差收敛的分量。通过仿真分析并与传统迭代学习控制进行比较,证明了本文方法具有更快的收敛速度,能够以较少的迭代次数实现直线电机的高精度跟踪控制。
永磁直线同步电机(PMLSM);迭代学习;改进经验模态分解;收敛速度
0 引言
随着高速高精密加工技术的快速发展,永磁直线同步电机(permanent magnet linear synchronous motor, PMLSM)展现出取代传统运动执行器(如旋转式电机加螺杆或传导丝杠)的趋势[1]。PMLSM以其高速度、高精度和强推力等优点,在工业机器人、运送传输设备和磁悬浮列车等领域得到广泛应用。然而,由于PMLSM缺乏机械传动环节,它无法缓冲内部参数变化及外部非线性扰动等因素的影响,这增加了伺服控制的难度[2]。
迭代学习控制(iterative learning control, ILC)利用之前迭代的数据,在连续重复任务中改善当前系统的控制输入信号,从而抑制重复性干扰,并实现在有限范围内的完全跟踪[3-5]。然而,ILC的积分特性可能放大非重复性扰动,从而影响系统的鲁棒性。文献[6]提出一种基于扩张状态观测器的数据驱动ILC方法,它能有效抑制系统的随机扰动,但未考虑时间滞后的影响。文献[7]在PMLSM伺服系统中引入Smith预估器,以减少ILC过程中时间滞后效应的累积影响,但该方法的设计需要系统具有精确的过程模型。此外,文献[8]提出一种无模型数据驱动的自适应ILC方法,避免了由于模型不准确而导致系统性能下降的问题,但该方法无法抑制非重复扰动。文献[9]通过设计时域补偿器来补偿ILC过程中的干扰,提高系统对非重复扰动的鲁棒性,但该方法未考虑误差的累积影响。
由于系统动态特性的变化或外部扰动的存在,ILC可能导致误差在每次迭代中逐渐累积,进而对PMLSM伺服系统的跟踪精度产生不利影响。为了解决这一问题,本文提出一种基于改进经验模态分解(modified empirical mode decomposition, MEMD)的迭代学习控制策略。首先,设计一种自适应比例微分(proportional differential, PD)型迭代学习位置控制器;然后,利用改进经验模态分解算法对跟踪误差信号进行分解,剔除发散的误差分量,并重新应用于迭代学习过程中;最后,通过仿真证明所提方法的有效性。
1 PMLSM数学模型
基于d=0的矢量控制,PMLSM在dq坐标系下的电压方程为[10]
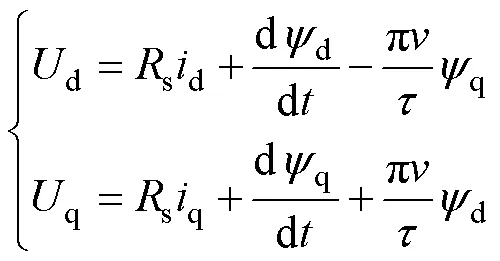
其中

式中:d、q为d、q轴的电压;d、q为d、q轴的电流;d、q为d、q轴的电感;s为动子相电阻;d、q为d、q轴的磁链;为动子线速度;为极距;f为永磁体磁链。
电磁推力e为
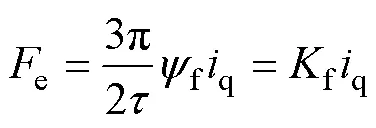
式中,f为推力系数。
PMLSM的机械运动方程为

式中:为动子质量;v为摩擦阻力系数;L为负载、端部效应及参数失配引起的干扰。
结合式(3)和式(4),可得PMLSM的数学模型为
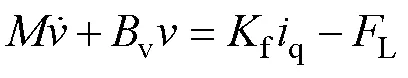
因此,PMLSM的传递函数为

2 迭代学习位置控制
为了减少PMLSM在重复任务中的位置跟踪误差,本文采用ILC设计一个位置控制器。PMLSM自适应迭代学习控制系统框图如图1所示,其中表示PMLSM的速度闭环,v为比例积分(pro- portional integral, PI)控制器。
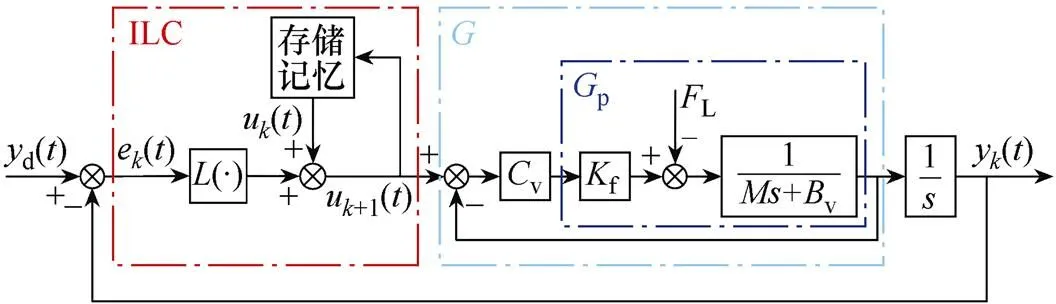
图1 PMLSM自适应迭代学习控制系统框图
由图1可知


本文提出的自适应PD型学习律为
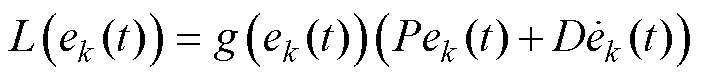

式中:、为学习增益系数;(×)为与误差边界相关的函数。
3 基于MEMD的迭代学习控制
为了减少误差积累效应[11]的影响,提出一种基于MEMD的迭代学习控制策略,以提升系统的位置跟踪性能。
3.1 MEMD算法
MEMD算法是一种用于信号分解的数据分析方法[12],旨在将非线性或非平稳信号分解为一组本征模态函数(intrinsic mode function, IMF),每个IMF代表一个具有不同频率和振幅的本征模态。本文提出基于三角极值波延拓与互补集合经验模态分解的MEMD算法。
1)三角极值波延拓的端点效应改进算法
端点效应会导致信号的上下包络线向两端发散,且该效应可延伸至下次分解的过程中,使分解效果不断变差[13]。为了抑制端点效应,本文利用三角极值波延拓法进行处理,其示意图如图2所示。
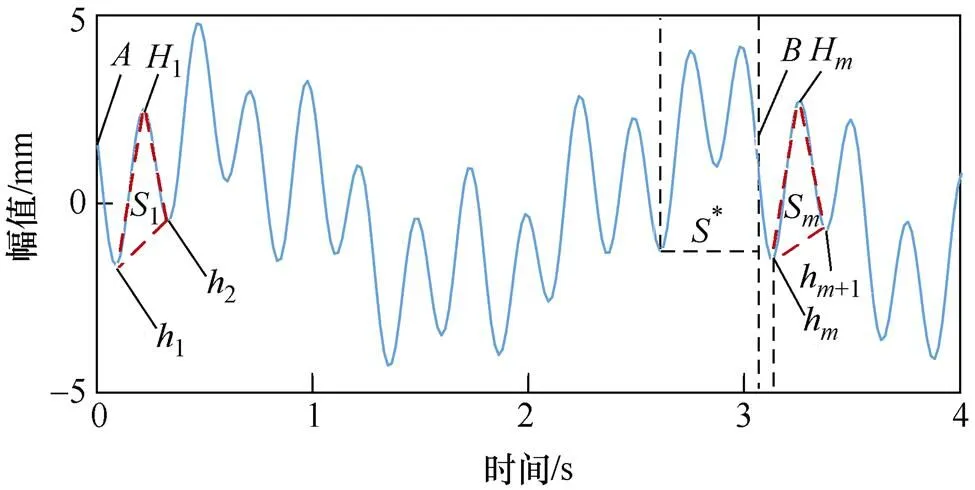
图2 三角极值波延拓法示意图
以数据左端点为例,波形延拓方法步骤如下:
(1)提取信号所有极值点。
(2)选取距离左端点最近的三个极值点构成的波形1作为模板子波,并将其余与模板子波1相似的极值波定义为匹配子波。
(3)利用模板子波1中三个极值点构成的三角形△112作为匹配对象,选取边长、斜率、曲率作为特征量,计算匹配子波S中极值点所确定的三角形△hHh+1的匹配误差,其值越小,匹配度越高。匹配误差计算公式如下[14]。
边长匹配误差为

斜率匹配误差为

曲率匹配误差为
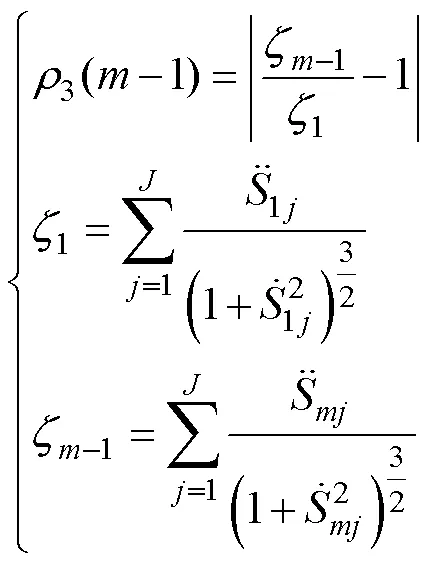

总体匹配误差为
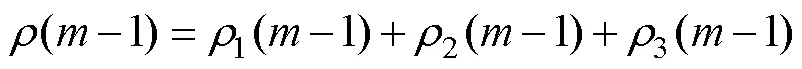
(4)波形延拓。设S为最佳匹配子波,确定延拓连接点,使端点处波形1与匹配子波左侧曲线Bh相对应,如图2所示,S即为左端延拓波形。
2)互补集合经验模态分解的模态混叠改进算法
模态混叠问题可能会造成错假的时频分布,导致信号分解结果失真[15]。本文采用的互补集合经验模态分解算法通过引入互补且独立分布的白噪声,使分解信号的极值点分布更趋匀称,从而抑制模态混叠问题,其过程如下:
(1)给定集合平均次数与白噪声的幅值。



(4)重复上述步骤次,得到2组IMF分量。最后将2组IMF分量进行多次集成平均处理,得到最终的IMF分量,即
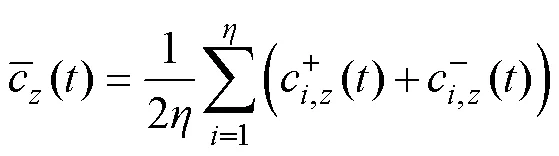
3.2 基于MEMD算法的迭代学习位置控制
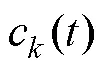
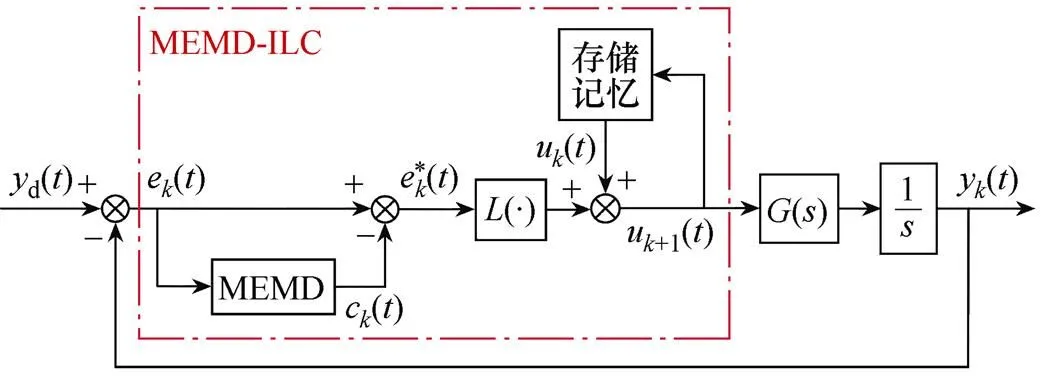
图3 基于MEMD算法的PMLSM迭代学习控制系统框图
基于MEMD算法的PMLSM迭代学习控制系统运行过程如下:
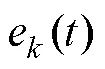
(4)利用重构的跟踪误差来计算控制输入,并将该控制输入应用于PMLSM迭代学习控制系统,可以实现更高效的学习。
4 仿真与分析


基于ILC方法的各次迭代跟踪误差的方均根(root mean square, RMS)见表1。根据表1可知,跟踪误差的方均根从未迭代的18.11mm减小到第10次迭代的4.73mm,减少了73.88%,但是其在第7、8次迭代时出现明显增加。

表1 基于ILC方法的跟踪误差方均根
图4为采用ILC方法经过10次迭代后的位置误差曲线,由图可知,最大位置跟踪误差约为6.53mm。

图4 基于ILC方法的位置跟踪误差曲线
利用MEMD算法分解各次迭代的跟踪误差,得到的IMF分量如图5所示。

图5 MEMD算法分解得到的IMF分量
从图5(a)可以明显观察到,在第7次和第8次迭代时,IMF1的幅值出现了递增现象。同样地,图5(b)显示在第7次迭代时,IMF2的幅值有所增加。此外,在图5(c)中,随着迭代次数的增加,IMF3的幅值呈现单调递减的趋势。这表明主要是IMF1和IMF2分量影响了迭代学习过程的单调收敛,从而降低了系统的学习性能。因此,需要在第7次和第8次迭代时消除IMF1分量,并在第7次迭代时消除IMF2分量。将递增的分量剔除后,重新运行系统,经过MEMD-ILC后系统跟踪误差的方均根见表2。
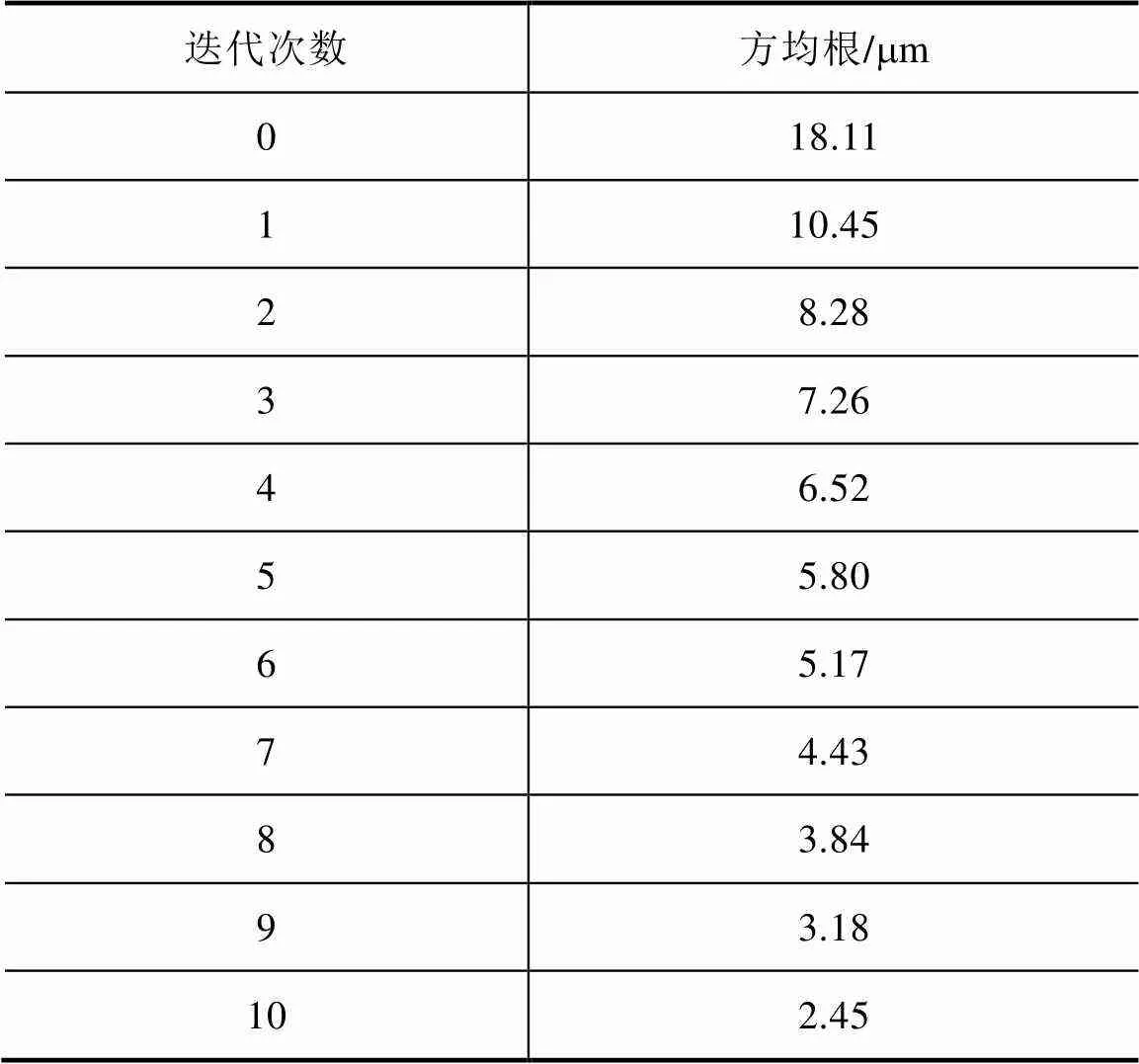
表2 基于MEMD-ILC方法的跟踪误差方均根
基于ILC和MEMD-ILC方法的跟踪误差方均根曲线如图6所示。
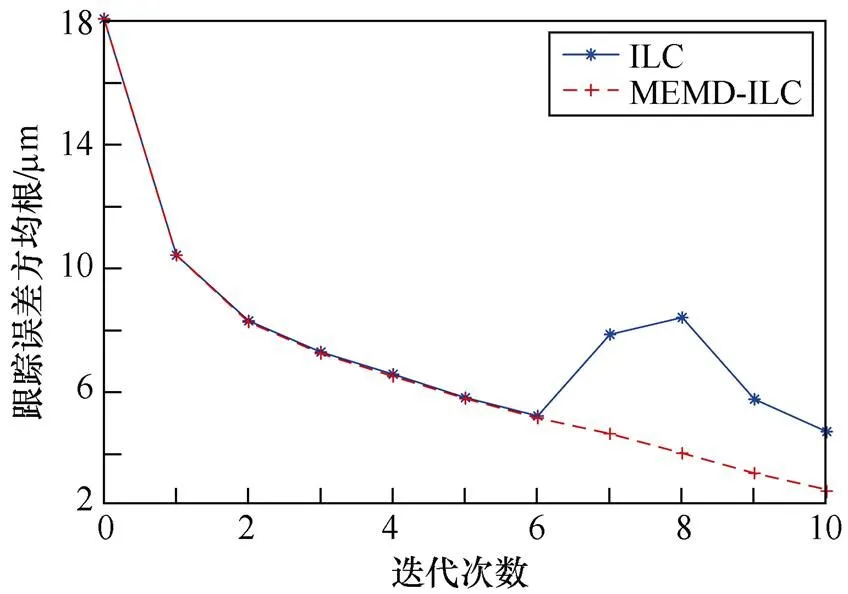
图6 基于ILC与MEMD-ILC方法的跟踪误差方均根曲线
通过图6可以观察到,经过MEMD算法处理后,随着迭代次数的增加,跟踪误差方均根从原来的不收敛变为单调递减;在第10次迭代时,跟踪误差方均根降低至2.45mm,与仅使用ILC方法相比,减少了48.2%。因此,MEMD-ILC方法明显改善了迭代效果。
基于MEMD-ILC方法的位置跟踪误差曲线如图7所示。由图7可知,基于MEMD-ILC方法的最大位置跟踪误差约为5.37mm,与图4相比,最大跟踪误差减少了17.76%,这表明系统的位置跟踪精度得到进一步提升。

图7 基于MEMD-ILC方法的位置跟踪误差曲线
5 结论
本文提出了一种基于MEMD算法的PMLSM迭代学习控制方法,旨在解决误差积累效应导致的收敛速度慢和跟踪性能差的问题。利用MEMD算法将各次迭代的跟踪误差进行分解,排除对系统收敛产生影响的误差分量,并重新整合剩余的误差分量,以提高迭代学习控制的收敛效果和跟踪精度。仿真结果表明,相较于传统的ILC方法,采用MEMD-ILC方法的位置跟踪误差减少了17.76%,PMLSM系统的位置跟踪精度得到有效提升。
[1] 黄旭珍, 张成明, 梁进, 等. 考虑定位力及摩擦力的永磁同步直线电机系统预定位估计算法[J]. 中国电机工程学报, 2021, 41(4): 1496-1504.
[2] 赵牧天, 葛琼璇, 朱进权, 等. 中速磁悬浮列车分段式长定子永磁直线同步电机牵引控制策略[J]. 电工技术学报, 2022, 37(10): 2491-2502.
[3] 贺玉晓, 王丽梅. 永磁直线同步电动机迭代超螺旋滑模控制[J]. 电气技术, 2022, 23(6): 24-29.
[4] 武志涛, 杨兆宁. 永磁直线同步电机的双闭环鲁棒补偿控制[J]. 电机与控制学报, 2022, 26(3): 101- 108.
[5] 金鸿雁, 赵希梅, 王天鹤. 基于扰动观测器的永磁直线同步电动机自适应反推互补滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2356-2365.
[6] HUI Yu, CHI Ronghu, HUANG Biao, et al. Extended state observer-based data-driven iterative learning control for permanent magnet linear motor with initial shifts and disturbances[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1881-1891.
[7] 赵希梅, 马志军, 朱国昕. 永磁直线同步电机自适应PD型迭代学习控制[J]. 沈阳工业大学学报, 2016, 38(1): 7-12.
[8] FU Xuewei, YANG Xiaofeng, ZANCHETTA P, et al. Frequency-domain data-driven adaptive iterative learning control approach: with application to wafer stage[J]. IEEE Transactions on Industrial Electronics, 2020, 68(10): 9309-9318.
[9] LIU Weike, XU Yunlang, DING Runze, et al. Time- iteration-domain integrated learning control for robust trajectory tracking and disturbance rejection: with application to a PMLSM[J]. IET Control Theory & Applications, 2021, 15(18): 2344-2354.
[10] 张育增, 周睿智, 李帅. 永磁同步直线电机模糊滑模速度控制研究[J]. 电气技术, 2020, 21(12): 23-29.
[11] 王丽梅, 孙璐, 初升. 基于经验模态分解算法的永磁直线同步电机迭代学习控制[J]. 电工技术学报, 2017, 32(6): 164-171.
[12] 郑近德, 应万明, 潘海洋, 等. 基于改进全息希尔伯特谱分析的旋转机械故障诊断方法[J]. 机械工程学报, 2023, 59(1): 162-174.
[13] ZHANG Xuejun, HUO Yan, WAN Dongsheng. Improved EMD based on piecewise cubic Hermite interpolation and mirror extension[J]. Chinese Journal of Electronics, 2020, 29(5): 899-905.
[14] 宿文才, 张树团, 刘陵顺. 基于改进极值波延拓的极点对称模态分解端点效应抑制方法[J]. 电工技术学报, 2020, 35(增刊1): 294-301.
[15] 杨逸帆, 赵兵兵, 康迪, 等. 基于改进希尔伯特-黄变换的电力系统谐波检测系统设计[J]. 电气技术, 2022, 23(5): 9-17.
Iterative learning control of linear motor servo system based on modified empirical mode decomposition
LIU Sinuo WU Zhitao
(School of Electronics and Information Engineering, University of Science and Technology Liaoning, Anshan, Liaoning 114051)
In order to address the issue of low convergence speed and poor tracking performance caused by error accumulation effects in iterative learning control of linear motor servo systems, a method based on a modified empirical mode decomposition algorithm is proposed. Firstly, a self-adaptive iterative learning position controller is designed. Subsequently, an improved algorithm based on the extension of triangular extreme wave and complementary set empirical mode decomposition is proposed. This algorithm can decompose the tracking errors of each iteration, screen and eliminate the components that affect error convergence. Through simulation analysis and a comparison with traditional iterative learning control, the paper demonstrates that the proposed method exhibits faster convergence speed and can achieve high-precision tracking control of linear motors with fewer iterations.
permanent magnet linear synchronous motor (PMLSM); iterative learning; modified empirical mode decomposition; convergence speed
2023-12-22
2024-01-08
刘思诺(1999—),男,河北秦皇岛人,硕士研究生,主要研究方向为永磁直线同步电机控制。
国家自然科学基金项目(51677122)

