湖南省大区域三维水汽层析反演及降雨预报应用

吴 皓 陈必焰 黄 宁，3 谭井树 靳文凭 陈春花

（1.湖南安全技术职业学院，长沙 410151；2.中南大学地球科学与信息物理学院，长沙 410083；3.北斗高精度卫星导航与位置服务湖南省工程研究中心，长沙 410018；4.湖南北云科技有限公司，长沙 410205；5.湖南省测绘科技研究所，长沙 410018）

0 引 言

水汽在地球大气中含量虽然较少，但由于水汽的相变效应，具有雨、雾、云、雪等各种状态，它的变化对大气热量传递、辐射平衡和能量循环起着关键作用，同时也是灾害性天气形成和演变的主要驱动力[1-2]。在天气预报中，大气中水汽含量及时空分布变化直接影响数值预报的准确性，获取高精度的大气水汽含量对于做出更加准确的气象预报和加强极端天气灾害的认知预知具有重要意义[3]。传统气象预报采用的水汽信息主要来自探空站获取的水汽廓线，其时间和空间分辨率都相对较低。全球导航卫星系统（Global Navigation Satellite System，GNSS）水汽探测技术发展30 多年来，大量研究已经证明其反演的大气可降水量（Precipitable Water Vapor，PWV）精度可达到1～2 mm[4-5]，同时具有高时空分辨率和全天候作业的优点。因此GNSS 技术获取的PWV 可作为常规探空资料的重要补充，为气象部门做出更准确的气象预报提供丰富可靠的水汽资料。

基于地面密集的GNSS站网获取的水汽数据为层析技术提供了一种获取高精度和高时空分辨率大气水汽分布的重要数据源。Flores 等[6]最早在地基GNSS 层析水汽方面开展了研究，采用了附加约束条件的层析算法，并利用欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）预报结果证实了层析技术可以用来监测对流层水汽的时空变化。宋淑丽[7]利用上海地基GNSS 观测网进行了水汽层析的试验，并首次获得了上海地区的水汽三维分布。Champollion 等[8]利用法国南部的一个小区域密集GNSS 观测网进行了水汽层析实验，成功获得了大气水汽的四维分布结构，并发现了GNSS 水汽层析结果与气象事件的相关性。由于水汽层析技术获得的水汽场包含了十分可观的大气水汽三维分布信息量，使得其在天气预报模式数据同化、区域水汽多维动态变化反演，以及降雨事件监测预警预报等方面具有极大的应用潜力[9]。近20 年，研究者们在GNSS 水汽层析技术的各方面开展了大量的研究工作，致力于不断完善GNSS 水汽层析技术及提高层析结果的精度和可靠性[10-16]。

降雨发生过程中常常伴随着大气水汽的聚集、凝结和蒸发等变化[17]，研究水汽与降雨事件之间的关联性有助于提高降雨监测及预报的能力。地基GNSS 网具备监测中小尺度天气水汽变化和运移的能力，GNSS 水汽产品提供的湿度信息可有效应用于降雨时空变化分析及短时临近降雨预报研究中[18]。研究人员通过对GNSS PWV 与降雨量一维时间序列的对比分析发现，两者的时间变化具有良好的匹配性，在发生强降雨事件之前往往存在PWV 明显变化的现象，并指出其可用于短期降雨预报研究[19-20]。基于连续运行参考站网获取的二维PWV 平面分布可以反映出区域内水汽含量的时空变化，研究发现强降雨发生区域与PWV 高值区十分吻合，说明利用密集的GNSS 观测网络获取的PWV 在降雨落区预报中具有极大的应用潜力[21]。而随着水汽层析技术的发展，三维水汽层析产品能够获取更精细的水汽场，可为降雨预报提供丰富且细致的水汽变化信息。如陈必焰等[22]通过分析香港地区2010—2014 年3 次强降雨（每次事件都观测到大于50 mm/h的降雨量）时水汽场的时空演变特征，证明了层析技术可以很好地探测降雨时水汽的时空变化。

本文基于GNSS 水汽层析技术，结合湖南省连续运行基准站（HNCORS）观测数据、风云4A（FY-4A）水汽产品、探空水汽廓线等多源数据，反演了湖南省2020年6月高时空分辨率的水汽分布场并进行了精度验证。进一步利用水汽层析产品、卫星降雨量和ECMWF 第五代再分析产品（ERA5）的气象数据，基于BP 神经网络建立了短时降雨预报模型，实现湖南省大范围降雨落区预报。

1 GNSS水汽层析模型构建方法

GNSS 卫星的电磁波信号在传播过程中会受到对流层中干性气体和水汽的影响而产生路径延迟。在GNSS 高精度数据处理中，可采取双差或精密单点定位模式估计对流层延迟，进而利用经验干延迟模型提取出PWV。借助映射函数，可将测站上空的PWV 投影到GNSS 信号路径上，从而得到斜路径大气可降水量（Slant Water Vapor，SWV）。沿着GNSS 接收机到GNSS 卫星射线路径l，SWV与水汽密度ρw之间的关系可用积分表示为[11]：

常规层析方法是在研究区域建立格网模型，并假设在层析时段内每个体素内水汽密度不变且均匀分布，则层析方程中每一个体素的水汽密度为未知待解参数。通过计算SWV穿过每个体素的截距，SWV的积分可以近似为：

式中：SWVi为第i条射线的斜路径大气可降水量；ΔSi,j为第i条信号线穿过第j个网格的截距；xj为第j个网格的水汽密度未知数。对所有SWV 射线建立与水汽密度参数之间的关系后即可得到层析观测方程组：

式中：B为观测方程系数矩阵；X为网格水汽密度参数向量。

由于GNSS 站点分布不均匀且GNSS 信号呈现“倒锥形”的特征，无法保证每一个体素都有GNSS 射线穿过，尤其是位于模型侧边和底部的体素。因此，仅依靠GNSS射线建立的层析方程组往往存在不适定性问题，不能用最小二乘法直接解出。为了解决这一问题，可以通过构建经验性的约束使方程组达到有解的条件。联合GNSS 观测方程以及约束条件可得：

式中：Hh和Hv分别为水平和垂直约束系数矩阵。在水平方向上，通常假设某个体素的水汽密度与其周围体素的水汽密度密切相关，距离越近相关程度越高，Hh的组成元素可采用高斯加权函数来计算[23]：

式中：i、j、k为当前所计算网格的位置；in、jn、k为水平方向上其他网格的位置；din,jn,k为当前网格到其他网格的距离；n和m为水平方向上网格的维数；σ为平滑因子，根据平稳假设范围给定，一般设置为1.5 倍网格水平长度；当i=in且j=jn时，hin,jn,ki,j,k取值为1。垂直方向上，大气水汽近似呈指数递减的规律：

式中：Ns为地表水汽密度；z为垂直高度；hsc为水汽标高，可由历史观测资料得到。在同一垂直网格纵列中，根据指数递减规律，可得到相邻网格水汽密度的关系如下：

式中：xi,j,k和xi,j,k+1为垂直方向上相邻网格水汽密度参数；hk和hk+1为对应网格垂直高度。在加入约束条件之后，上述层析方程组的病态问题得到解决，可以用最小二乘方法直接解算。

在常规层析模型的基础上，将FY-4A反演的高时空分辨率分层PWV（Layered PWV，LPW）数据融合到层析模型作为附加观测进行联合层析反演。FY-4A 提供3种LPW 产品，即低层可降水量（LPW_LOW：地表～900 hPa），中层可降 水 量（LPW_MID：900～700 hPa）和 高 层 可 降 水 量（LPW_HIGH：700～300 hPa）。由于LPW 的边界是基于气压高度划分，需要将其转换为层析模型的几何高度。本研究利用ERA5 气压分级位势数据插值得到上LPW 数据气压边界处的位势，并使用下式近似得到相应几何高度H：

式中：φ为FY-4A LPW数据边界处位势；g为重力加速度。

在高水汽含量时FY-4A PWV 存在较为严重的偏差，因此在层析过程中需要对FY-4A水汽观测值进行校正。采用文献[24]中提出的PWV 大于50 mm 的校正模型对FY-4A PWV 进行实时校正，得到每个层析历元中FY-4A PWV的改正数VPWV。由于FY-4A PWV 等于3 种LPW 之和，为得到每个LPW 的改正数，忽略LPW 观测之间的相关性，使用误差传播定律进行改正数的分配：

式中：VLPW_LOW为LPW_LOW 的改正数，σLPW_LOW、σLPW_MID和σLPW_HIGH分别为利用探空数据评估得到的LPW_LOW、LPW_MID 和LPW_HIGH 的中误差，分别取1.23 mm、2.01 mm、1.59 mm。

综合GNSS SWV 与FY-4A LPW 观测方程及约束条件，得到融合FY-4A LPW数据的水汽层析函数模型[23]：

式中：BGNSS、BFY-4A分别为GNSS、FY-4A 观测方程系数矩阵；X为水汽密度未知数向量；SWVGNSS为GNSS SWV 观测值；LPWFY-4A为FY-4A LPW 观测值；Hh、Hv为约束方程系数矩阵；Rv为垂直约束常数矩阵。

考虑到FY-4A 与GNSS 水汽数据存在精度上的不一致，因此还需要合理确定两类数据的权比。基于文献[24]中对FY-4A PWV 产品精度评估得到的结论，将FY-4A PWV与GNSS PWV 相对于探空资料的中误差作为定权依据。具体方法为：

式中：pGNSS和pFY-4A为层析方程组中GNSS观测值和FY-4A观测值的权，σGNSS和σFY-4A为GNSS和FY-4A PWV 相对于探空数据的中误差，分别为2.53 mm和3.95 mm。

2 GNSS层析精度验证

2.1 研究区域及层析实验简介

湖南省位于我国中南部，为亚热带季风湿润气候，天气复杂多变，雨水集中，暴雨灾害频发。受季风影响，湖南省区域上空的水汽具有非常不稳定的时空变化，因此及时准确地监测大气水汽的变化对气象灾害预警极其重要。HNCORS 共有124 个站点，平均间隔距离为41 km，如图1所示。层析实验时段为2020 年6 月1—30 日，共30 d。本研究采用Bernese 52高精度数据处理软件进行HNCORS观测数据的解算，将生成的对流层延迟文件和残差文件用于水汽层析中。

图1 HNCORS站点分布及层析水平格网划分示意图

层析区域水平范围设置为经度108.85°E—114.05°E、纬度24.85°N—30.05°N。层析网格划分方式为：经度与纬度方向均匀划分，网格间隔均为0.4°，网格数均为13个。在垂直方向上，本研究参考了文献[16]的实验方案，设置网格底部和顶部的高度分别为0 m 和11 000 m。考虑到水汽在垂直方向上的指数分布特征，采用下密上疏的不均匀分层方式进行网格划分，网格间距具体为：400 m、400 m、400 m、500 m、500 m、500 m、500 m、700 m、700 m、700 m、700 m、1 000 m、1 000 m、1 000 m、2 000 m，共计分为15层。整个实验区共划分为13×13×15=2 535 个体素，即2 535 个水汽密度参数。

由于采用代数重构法解算层析方程组需要提供迭代起始时刻的水汽密度初值，而且层析结果的精度很大程度上依赖于初始值的准确性[25]。因此本研究使用层析方程组的最小二乘解作为迭代初始值，利用乘法代数迭代算法（Multiplicate Algebraic Iterative Technique，MART）对初始水汽密度场进行迭代修正。从2020 年6 月1—30 日进行连续层析成像，获取时间分辨率为30 min 的大气水汽密度场。每天协调世界时（UTC）0 时刻使用探空先验约束，当天内的其他历元则以上一历元得到的层析结果为垂直约束，即相当于每天利用探空数据进行1 次初始化，从而避免误差累积过大。为验证上述层析模型的可行性，使用传统层析模型进行对照实验，两种模型的唯一区别为有无添加FY-4A LPW，其他设置相同。

层析时间段内，研究区共有3 个可用的探空站（图1），分别是湖南怀化站（RSHH）、湖南郴州站（RSCZ）及广西桂林站（RSGL）。仅使用探空数据只能在少数几个站点处验证层析的精度，无法评估层析的整体精度及其空间分布，因此本文同时利用ERA5数据进行精度检验以获取层析结果误差的三维分布。精度验证所用的ERA5 数据为不同气压级的温度和相对湿度参数，空间分辨率为0.25°×0.25°，时间分辨率为1 h，计算出水汽密度并插值到每个层析网格中心点处[26]。

2.2 探空数据评估结果

以湖南省内的3 个探空站点的水汽廓线数据为真值，并根据水汽廓线内插得到各垂直网格中心点处的水汽密度参考值，对本研究中两种层析方案的结果进行精度评定。图2 展示了2020 年6 月1 日UTC 12 时传统模型与新模型在3 个探空站点处层析垂直水汽密度廓线的结果对比。图中黑色曲线代表探空水汽密度廓线，蓝色曲线代表传统层析模型结果，红色曲线为本研究提出的新模型层析结果。两种层析方案的水汽密度在不同高度上的变化趋势均与探空水汽密度具有很好的一致性，但新模型的结果与探空水汽廓线更为符合，即在大多数情况下，加入FY-4A 水汽产品能够有效地改善层析解的精度，得到更加符合实际的三维水汽分布。

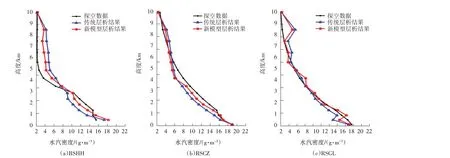
图2 传统模型与新模型在3个探空站点处的层析垂直水汽密度廓线对比结果

图3 显示了传统模型与新模型均方根误差（Root Mean Squared Error，RMSE）和相对RMSE（R-RMSE）随高度的变化。R-RMSE定义为每层的RMSE除以该层对应的探空平均水汽密度。由于本研究在层析模型中加入了顶层约束，即顶层的水汽密度设置为0.05 g/m3，因而在图中出现的顶层RMSE与R-RMSE明显小于次顶层的情况是合理的。传统层析方案中，中层高度的RMSE小于低层和高层的RMSE，说明传统方案在低层和高层的水汽层析上存在一定的难度。新模型的RMSE从低到高呈现逐渐减小的趋势，在不同高度上的RMSE均小于传统方案，并且低层和高层的RMSE减小幅度明显。

图3 两种模型层析结果在不同高度处的RMSE与R-RMSE对比

新模型的R-RMSE在各高度层同样均小于传统方案，同时两种方案的R-RMSE均出现随高度增加而增大的趋势，尤其在6 km 以上，R-RMSE均超过了100%。这表明在水汽含量较小的情况下，层析模型的一个小误差就会导致上层水汽密度的反演值出现较大差异。

进一步比较层析结果与探空数据的整体精度，图4 为1个月内层析水汽密度与探空水汽密度的误差统计与相关性分析结果。两种模型的结果均与探空结果具有极强相关性，相关系数分别达到了0.968 和0.984。从散点拟合直线结果来看，新模型的斜率（0.97）要比传统模型斜率（0.92）更接近于1。传统模型与新模型的RMSE分别为1.63 g/m3与1.18 g/m3，新模型的RMSE降低幅度为27.61%。由此可见，与探空数据相比，添加FY-4A LPW 数据的新模型层析结果的整体精度优于传统模型。

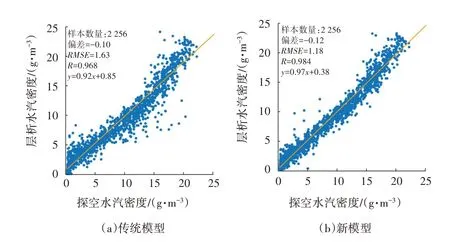
图4 两种模型层析结果与探空数据的水汽密度对比散点图

2.3 ERA5产品评估结果

图5 显示了研究区内ERA5 和两种层析模型之间水汽密度差值RMSE的分布。RMSE的计算方式为在每个水平网格上，统计该网格上的所有垂直体素。传统层析模型与新模型的RMSE分别在1.18～3.64 g/m3和1.14～2.68 g/m3的区间范围内变化。对于传统模型而言，位于湖南省内的网格的RMSE具有较大的数值，说明随着层析历元的增加，仅通过GNSS 观测值修正的水汽密度误差随之增大，尤其是在湖南北部和西部地区。而位于湖南省外的网格（例如研究区西南部）的RMSE相对较小，是因为这些区域缺少GNSS 信号的穿过，其误差主要是初始背景水汽场与ERA5的误差。对于新模型而言，在几乎所有区域，新模型的RMSE都比传统层析模型的RMSE小，说明融入FY-4A LPW数据对层析的整体精度改善明显。

图5 两种模型层析结果与ERA5数据比较的RMSE平面分布对比

图6 对不同垂直高度的平均精度进行了统计。与传统层析模型相比，新模型在近地层（0～3 km）及高层（6 km 以上）的RMSE明显减小，而在中层（3～6 km），RMSE较为接近。R-RMSE的垂直分布同样具有上述特征，但就降低幅度而言，由于高层水汽量较小，R-RMSE降低幅度比近地层大。经统计，传统模型和新模型层析结果的平均RMSE分别为2.77 g/m3和1.71 g/m3，新模型的精度提升幅度达到了38.27%。总体来说，融入FY-4A LPW 的新层析模型极大地提高了三维水汽层析场的质量，特别对近地层与高层的层析精度改善效果尤为明显。

图6 两种模型层析结果在不同层析高度处的RMSE与R-RMSE对比

3 基于层析产品的降雨预报

3.1 降雨预报模型构建

采用BP 神经网络进行降雨预报首先需要确定网络结构。相关参数包括每个网格的PWV、PWV 变化率、温度、露点温度和气压。为实现对整个研究区域内降雨落区的预报，每个网格中心的经度和纬度也作为输入参数。另外，由于地形对降雨也有一定影响，同样也设为输入参数。因此预报模型的输入参数为PWV、PWV 变化率、温度、露点温度、气压、经度、纬度和高程总共8 个，即BP 神经网络输入层的节点数量为8 个。隐含层节点数量的设定对网络模型至关重要，隐含层节点按照Kolmogrov 定理给出的与输入层节点个数的等式关系确定：

式中：Nhide与Ninput分别为隐含层与输入层节点数量，因此本研究中隐含层节点数量确定为17；降雨量为模型的唯一输出参数，输出层节点数为1，降雨量数据来源于全球降水测量（Global Precipitation Measurement，GPM）计划的降水产品，该产品基于地面雨量站数据进行了校正，总体精度较高，时间分辨率为30 min，空间分辨率为0.1°×0.1°[27-28]。BP 网络学习算法选择为兼具牛顿法局部收敛性与梯度下降法全局性的Levenberg-Marquardt算法。

由于PWV 的显著增长或降低通常是发生在降雨事件之前，因此本研究的输入参数PWV 为预报时刻前6 h 内的最大值，PWV变化率为最大值减去最小值后除以它们的时间间隔，而输出参数降雨量为后3 h内的GPM累计降雨量。每个层析平面网格被视为一个样本采集单元，以30 min 分辨率进行样本采集。本研究将2020 年6 月1—20 日共20 d的数据作为训练样本，2020年6月21—30日共10 d的数据作为模型测试样本。通常，降雨样本数量远小于无降雨样本数量，如果直接将其输入模型进行训练则会导致预测结果偏向于无降雨结果，因此本研究对无降雨样本进行随机降采样处理，使得降雨样本数量与无降雨样本数量达到相同大小后组成训练样本。本研究的重点是某个区域是否发生降雨，而不是降雨的大小。因此，实际和预测的降雨结果被视为二元值，即未发生降雨为0，发生降雨为1。由于预测的输出结果不会固定为0 和1，因此当输出值小于0.5 时视为预测无降雨，大于0.5时则视为预测降雨。

3.2 降雨预报结果分析

为了评价模型的预报精度，需要建立预测精度评估指标，本研究使用正确率（Correct Rate，CR）和误报率（False Alarm Rate，FAR）：

式中：Ny为实际降雨的总次数；Nyy为正确预测降雨的次数，即预测降雨的同时实际也发生了降雨；Nn为实际没有发生降雨的总次数；Nny为实际没有发生降雨的情况下预测发生了降雨的次数，即错误警报。

利用上述模型对2020 年6 月21—30 日期间研究区域的降雨进行预报，统计得到所有测试样本的平均CR为0.82，平均FAR为0.42。图7 给出了每个预报时刻的CR、FAR和区域累计降雨量（区域内每个网格降雨量之和）的时间序列图，图8 显示了几个具体预报时刻的模型预报与实际降雨落区平面图。6 月21—24 日4 d 内模型预测的CR处于较高水平，FAR同样也相对较高且波动更为剧烈，同时累计降雨量较大，说明这期间的天气形势非常不稳定，特别是22 日强降雨过后，2020 年6 月23 日UTC 10 时附近几小时降雨量相对较少，但模型极有可能将未降雨的情况预报为降雨。如图8（a）、图8（b）所示的情况，由于天气情况不稳定，模型将区域大面积预测为降雨，但实际上这期间未发生大范围降雨，虽然CR得分为0.94，但是FAR则达到了0.85，产生了大量虚假警报。25 日、28 日和30 日期间的总体预报精度最好，CR的得分较高且FAR相对处于较低水平。如图8（c）、图8（d），图8（g）、图8（h）所示，模型预报的降雨落区与实际降雨落区非常吻合，25 日UTC 08 时CR得分达到了0.98，同时FAR仅为0.17，28日UTC 08时的CR得分为0.90，FAR也仅为0.19。26 日、27 日及29 日期间，CR得分大部分较低，这是由于此期间降雨相对较少。如图8（e）、图8（f）所示，2020 年6 月26 日UTC 19 时的CR得分为0.35，FAR为0.24。因此当区域内降水较少时，模型很难捕捉零散的级别非常小的降雨，最终导致预报的CR较低。根据气象部门对降雨等级的划分，每小时雨量大于0.25 mm 为中雨及以上等级降雨，由于本研究预报的是未来3 h内的降雨情况，因此进一步统计了未来3 h实际降雨超过7.5 mm 时的模型预报精度，结果显示CR为0.94，即模型能够较好地对中雨及以上等级的降雨进行准确预报。

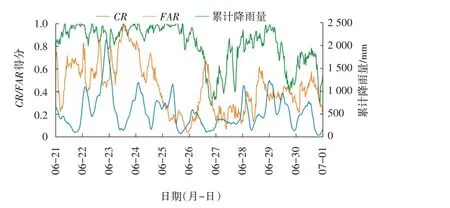
图7 降水预报CR、FAR及累计降雨量的时间序列

图8 模型预报与实际降雨落区平面图（绿色为降雨）

4 结 论

本文基于融合FY-4A 和GNSS 水汽数据的水汽层析模型，利用HNCORS 2020年6月的观测数据进行了水汽层析实验，分别采用传统层析模型和融合FY-4A的新模型获取了30 min 分辨率的大气水汽三维分布，并利用探空和ERA5数据对层析结果进行了精度分析。结果显示，相对于探空数据，传统模型与新模型的层析水汽密度平均RMSE分别为1.63 g/m3与1.18 g/m3，降低幅度达到了27.61%。相对于ERA5 数据，平均RMSE分别为2.77 g/m3和1.71 g/m3，降低幅度达到了38.27%。与传统模型相比，新模型明显地改善了近地层（0～3 km）及高层（6 km 以上）的层析结果。总体而言，融合高时空分辨率FY-4A LPW 的水汽层析模型极大改善了传统层析模型的不适定性问题，并可以获得更加接近于实际水汽分布的层析产品。

随着层析技术的发展，三维层析水汽产品因其具备高时空分辨率、高精度、近实时的特点，可为气象研究提供丰富而精细的大气水汽结构信息，具有极大的应用潜力。本文进一步利用层析PWV、PWV 变化率、温度、露点温度、气压、经度、纬度和高程等多种参数构建了BP 神经网络短时降雨落区预测模型，对湖南省进行了降雨预测实验。实验结果表明，该模型降雨预测CR为0.82，FAR为0.42，可以较好地对降雨的落区进行预测，同时能够正确预测超过94%中雨及以上等级的降雨事件，验证了使用层析产品进行大范围降雨落区预报的可行性。需要注意的是，形成强降水事件的过程是非常复杂的，仅利用层析产品很难对暴雨进行准确预报，下一步可结合气象雷达、风向仪等其他气象资料综合分析，以提高强降雨预报能力，进一步拓展GNSS气象学的应用范围。