车身多性能约束下的一体压铸三角梁轻量化设计
苏永雷 张志飞


摘要:
系統性地构建了一体压铸结构的优化方法,基于车身系统超单元模型实现多性能约束下的车身压铸件轻量化设计。首先,缩减复杂的车身系统,针对连续的车体结构,提出了子系统划分原则和方法,分别对各子系统进行超单元缩减,保证车身系统模型的分析精度并提高计算效率,为快速优化奠定基础;其次,同步考虑压铸结构单体性能和车身系统性能,采用折衷规划法归一化静动态子目标并构建综合目标函数,应用层次分析法得到子目标权重系数,进而开展了多模型拓扑优化,确定了加强筋位置分布;进一步地,同步考虑可设计与可制造性,对压铸结构变厚度拔模面进行参数化定义,并在优化过程中施加制造约束,基于构造的组合代理模型完成厚度参数设计。研究结果表明:在保证分析精度的前提下,缩减的车身系统模型可节省97.3%的计算资源;通过优化,在大幅提高车身一体压铸三角梁结构相关性能的同时,可实现轻量化,表明了所提方法的正确性和实用性。
关键词:压铸结构;模型缩减;拓扑优化;代理模型;轻量化
中图分类号:U462.2
DOI:10.3969/j.issn.1004132X.2024.04.012
开放科学(资源服务)标识码(OSID):
Integrated Casting Triangular Beam Lightweight Improving with
Multi-performance Constraints of Body Systems
SU Yonglei1,2,3 ZHANG Zhifei1
1.College of Mechanical and Vehicle Engineering,Chongqing University,Chongqing, 400044
2.Shanghai Xiaomi Intelligent Technology Co.,Ltd.,Shanghai,200012
3.Xiaomi Automobile Technology Co.,Ltd.,Beijing, 100000
Abstract: An optimization method of integrated casting structures was constructed systematically, and based on the super-element model of body system, body casting part lightweight improving with multi-performance constraints was realized. Firstly, complex body systems were reduced, the sub-system division principle and method were proposed for continuous body structure. Super-element reduction of the sub-system was conducted to ensure analysis accuracy and improve calculation efficiency, laying the foundation for rapid optimization. Secondly, performances of casting structures and body systems were considered simultaneously, the compromise programming methods were used to normalize static and dynamic sub-targets and construct the comprehensive objective function, weight coefficients of sub-targets were obtained by analytic hierarchy process(AHP), and then multi-model topology optimization was carried out to determine position distribution of reinforcements. Furthermore, designability and manufacturability were considered simultaneously, parametric definition of variable thickness drawing surface of casting structure was carried out, manufacturing constraints were applied during optimization processes, and then thickness parameter design was completed based on combined surrogate model. The results show that, under the premise of ensuring the analysis accuracy, reduced body system models improve computing efficiency greatly, and save 97.3% of computing resources. Casting triangular beam lightweight may be achieved while improving related performance by conducting structure optimization, which indicates correctness and practicability of the proposed method.
Key words: casting structure; model reduction; topology optimization; surrogate model; lightweight
收稿日期:20231012
0 引言
随着新能源汽车的高速发展,续航、产量、成本问题日益突出,一体化压铸结构轻量化降本提效优势凸显,促进一体压铸结构的应用范围不断拓展,如一体压铸后地板、一体压铸前舱等。随着一体压铸件尺寸的增大和集成化程度的提高,对免热处理多元合金材料、超大型压铸设备、压铸结构设计及成形工艺均提出了更高的需求。
关于铸造结构设计,拓扑优化方法是支撑结构创新设計的关键技术之一[1],众多学者针对不同的拓扑优化方法提出了多种处理方式。XU等[2]采用双向渐进优化方法对铸造约束的连续体结构进行了拓扑优化,可以有效求解多种连续体结构频率优化的收敛性问题。ZHANG等[3]考虑了几何形状要求和模具材料成本的制造约束,基于矢量法结合Heaviside函数,制订了铸件成形性约束条件,可根据用户需求权衡结构性能和制造成本。WANG等[4]针对复杂的多约束、多场问题, 引入一种由不同优化技术组成的求解算法,可在工程结构拓扑优化时兼顾结构性能和可制造性。马晶等[5]提出一种基于逆结构概念和附加重力场的铸造约束方法,保证了铸件结构拓扑优化解的可制造性。进一步地,WANG等[6]提出了基于水平集法的铸造零件结构形状和拓扑优化思路,可支撑结构性能和工艺制造的铸件设计。林佳武等[7]从耐撞性出发,通过拓扑优化,考虑压铸成形和连接工艺等要求,设计压铸铝合金后纵梁,实现了结构的模块化和轻量化。汽车具体的大型一体压铸结构需要满足多性能约束,与相邻部件间的耦合作用也需要考虑,且压铸结构的材料分布需兼顾可制造性和轻量化的需求,这对一体压铸件设计方法提出了新的挑战。
车身多性能约束下的一体压铸三角梁轻量化设计——苏永雷 张志飞
中国机械工程 第35卷 第4期 2024年4月
本文以机舱一体压铸三角梁为研究对象,对复杂的车身系统采用模型缩减方法,保证分析精度并提高计算效率;考虑压铸结构单体性能(等效静载能力)和耦合的车身系统性能(车身扭转刚度、车身局部模态等),通过多模型拓扑优化完善加强筋设计;考虑设计与可制造性,基于组合代理模型对各型面厚度进行参数设计;最终,三角梁结构设计实现性能与质量的平衡。
1 车身系统超单元模型搭建
1.1 压铸三角梁相关工况及性能定义
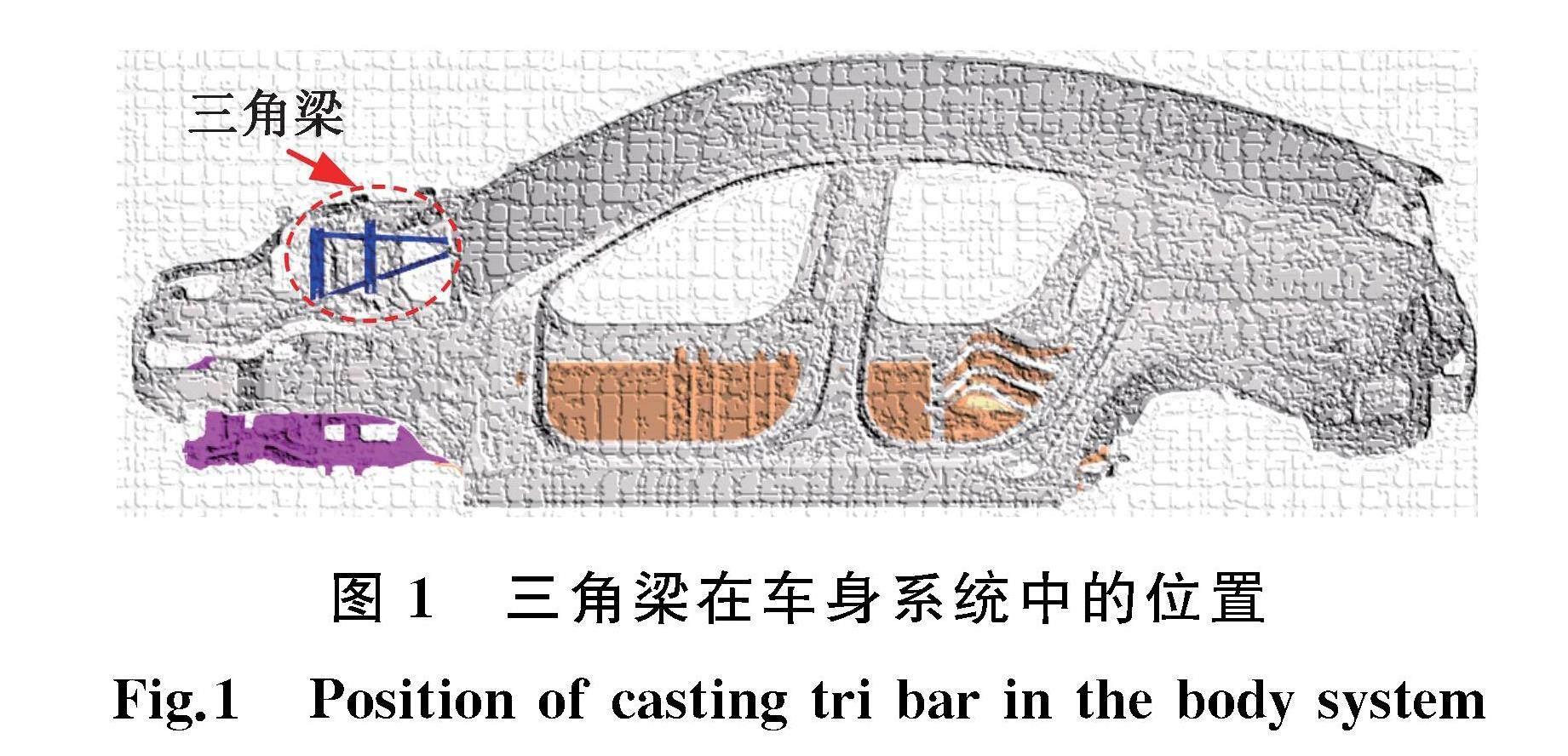
压铸三角梁是车身系统机舱区域的关键部件,在车身系统中的布置位置如图1所示,其结构设计不仅需要满足铸件单体性能及工艺制造性要求,还要考虑部件间的耦合作用及对整个车身系统性能的影响。
三角梁单体性能主要为碰撞等效静载工况的截面最大等效承载力。工况加载方法及初始设计方案如图2所示,将三角梁后端及横梁一端螺栓用工装夹具固定,在横梁另一端的夹具上在同一水平面内匀速静载施压,以等效偏置碰撞工况。
of initial concept design
关联的车身性能包括车身刚度、三角梁约束模态、三角梁动刚度等。压铸三角梁设计需要兼顾的典型性能及初始设计方案状态如表1所示,可以发现,初始设计方案的多项性能未达标,有必要开展结构优化,以满足性能需求。
车身系统有限元模型包含的单元网格数量较多,采用车身系统模型进行性能分析较为耗时,基于有限元法开展三角梁结构优化需要反复迭代,涉及大规模线性方程组的计算,其效率较低[8],提高大规模反复求解效率的一个可行途径是对结构进行降阶建模和分析[9]。
1.2 车身系统超单元创建
超单元技术是一种模型降阶求解方法,可以对模型自由度进行重新划分,即将一个复杂模型划分为多个子系统,各子系统再处理为超单元。此时,超单元自由度集合由边界面上的节点自由度集合和超单元内部自由度集合组成,将这些超单元利用有限元模型的对接方式与残余结构组合,最后进行求解,以达到提高计算效率且维持全模型计算精度的目的[10]。其中,子系统划分是车身系统超单元模型搭建的关键环节,通过划分将车身系统分为残余结构和相应的子系统超单元模型。一般情况下,子系统划分遵从以下原则[11]:①尽量减少超单元边界节点数量,以实现超单元模型自由度的高效缩减;②子系统划分应该保证部件结构的完整性,以便于模型管理、分析及优化。复杂车身系统中的副车架、电池包等典型子系统符合上述子系统划分原则,可以直接开展超单元建模。车体与副车架、电池包子系统之间存在固有边界,即子系统之间通过螺栓连接,则采用成对的RBE2单元进行螺栓模拟,将RBE2的主节点作为边界节点,进行子系统超单元求解。
车体子系统是一个连续结构,模型对象不存在固有边界,不符合上述子系统划分原则。本文提出连续体模型的子系统划分原则,以支撑车体子系统的进一步划分和缩减。对于近似等截面的连续结构(图3a),假定连续结构由连续体和结合面串联组成(图3b),则连续结构的综合刚度Kt符合下式:
1Kt=1Kl+1Km+1Kr(1)
式中,Km为结合面等效刚度;Kl、Kr为结合面两侧连续体的刚度。
根据应变能相等原则,结合面、连续体的等效刚度K均可以表示为[12]
K=ESh(2)
式中,S为横截面积;h为厚度;E为弹性模量。
结合式(1)、式(2)可得
1Kt=hlEmEr+hmElEr+hrElEmElEmErS(3)
式中,下标m、l、r分别表示结合面和结合面两侧连续体。
连续体结构中El≈Er,当结合面用刚性单元等效(图3c),即Em=+∞,且结合面厚度hmmin(hl,hr)时,则式(3)转化为
1Kt=hlElS+hrErS≈hl+hm/2ElS+
hr+hm/2ErS=1K*l+1K*r(4)
其中,K*l、K*r为考虑结合面时对应的两侧连续体的等效刚度,特别地,当hm=0时,1Kt=1K*l+1K*r,如图3d所示。
本文针对连续结构提出子系统划分原则如下:①尽量减少超单元边界节点数量,以便实现超单元模型自由度的高效缩减;②在近似等截面的区域进行划分,结合面用刚性单元等效,且结合面厚度接近或等于零。
根据以上原则,进一步对车体模型开展子系统划分。将A柱、门槛进行截断,以垂直于腔体中心线的平面为截面,并将界面节点投影到截面上,将车体模型划分为两部分子模型;分别在子模型的截面处建立RBE2单元,界面节点为RBE2的从点,腔体形心为主点;将两个子模型各截面处对应的RBE2单元主点通过共节点重新“缝合”起来,形成零厚度的结合面,则此时RBE2的主点可视为两个子模型的边界节点。前风挡或者顶棚刚度较低,借用截断A柱的截面,采用同样的方法设定边界节点,将包含设计对象(三角梁)的子模型设定为残余结构,另一子模型转化为超单元。此外,为使超单元模型的结果可视化,以及关键节点信息的方便读取,将各边界点、工况加载点及测量点通过PLOT单元依次连接并输出结果。
综上,可以采用本文提出的方法对存在固有边界的子系统进行模型缩减,并对连续结构的车体实现进一步模型缩减,将车体残余结构与车体超单元、副车架超单元、电池包超单元进行组合求解,见图4。得到相关的静力学分析及动力学分析结果,对比分析精度(表2)可以发现,车身系统进行超单元缩减后计算偏差较小,全局性能如车身弯扭刚度、车身弯扭模态计算偏差小于0.21%,局部性能如压铸三角梁模态及悬置点静刚度计算偏差极小;在保证分析精度的前提下,在计算效率方面,本文超单元方法可节省分析97.3%的计算时间,可大幅提高相关结构优化的效率。
2 压铸三角梁多模型多目标拓扑优化
以机舱区域的一体压铸三角梁为结构优化对象,考虑三角梁单体结构的性能以及与其他部件耦合作用的车身性能,开展相关工况的多目标拓扑优化,指导结构设计,其中车身性能的计算模型采用超单元模型以提高优化效率。
2.1 设计空间确定及制造工艺设定
三角梁端头位置通过螺栓固定在减振塔、流水槽上,压缩机通过悬置固定在三角梁框架内侧。为满足压力压铸过程材料成形质量需求,结构注塑主通道尽量连续,将各梁截面设计为U形,U形槽的下表面、侧面以最小工艺可实施厚度赋值,根据三角梁框架与其他部件装配和空间布置关系,定义截面、悬置及其他安装区域为非设计域,U形截面内部空间设计域定义为拓扑域X,如图5所示,通过拓扑优化以识别需要加强的局部区域,明确加强筋布置。
对于三角梁结构,必须考虑铸造工艺的拔模方向,保证装配便利性和加工可行性,本文在拓扑优化过程中添加+Z向拔模约束。
2.2 多目标拓扑优化模型
采用线性加权和法执行多目标设计具有一定局限性,不适用于子目标函数数量级不同的多目标优化问题[13]。本文采用折衷规划法研究多目标拓扑优化问题,得到以柔度最小为目标的静态工况拓扑优化数学模型[14]:
min C(ρ)=[∑mk=1wqk(Ck(ρ)-CminkCmaxk-Cmink)q]1q(5)
式中,ρ=(ρ1,ρ2,…,ρn)T为设计变量;n为单元总数;m为刚度工况总数;wk为第k个工况的权重因子;q为惩罚因子,对于体网格拓扑域,取q≥2;Ck(ρ)为第k个工况的柔度目标函数;Cmaxk、Cmink分别为第k个工况的柔度目标函数的最大值、最小值。
式(5)中,需要对碰撞等效靜载工况进行处理,将1 mm/ms的静压转变为1000 N的静载,保持同样的加载方向,将时域的静载工况转化为静态工况,以满足拓扑优化阶段的工况定义。
本文采用加权特征值的倒数定义模态工况优化问题,得到以加权特征值倒数最小为目标的动态工况拓扑优化数学模型:
min Φ(ρ)=∑jWjλj∑jWj(6)
式中,λj为第j阶模态的特征值;Wj为第j阶模态的权重系数。
根据压铸三角梁模态特征,目标函数主要考虑表2中对应的3阶模态特征值。
考虑到子目标函数相对重要性,引入权重因子w,构建多工况柔度最小化与多阶特征值倒数最小化的综合目标函数:
min f(ρ)={w2[∑mk=1wk(Ck(ρ)-CminkCmaxk-Cmink)]2+
(1-w)2(Φ(ρ)-ΦminkΦmaxk-Φmink)2}1/2(7)
综合目标函数的各子目标都对应着一个权重系数,本文应用决策论中的层次分析法[14],参考文献[15]对子目标的相对重要性的定义,采用成对比较法建立静态工况子目标矩阵S和动态工况子目标决策矩阵D,表示为
S=11/331/31/71/71/71/73151/31/31/31/31/31/31/511/71/91/91/91/933711/31/31/31/373931111739311117393111173931111
D=131/71/311/9791
对矩阵进行一致性检验[16],发现矩阵一致性比值均小于0.1,判定矩阵一致性满足要求;矩阵最大特征值对应的归一化特征向量就是各子目标的权重比,得到动态工况3阶模态和静态工况8个子目标权重系数,如表3所示。另外,定义子目标函数的权重因子w=0.5。
2.3 多目标拓扑优化
多模型优化(multi-model optimization, MMO)可以同时兼顾多个计算模型,这些模型共享部分设计变量,共享的设计变量会得到相同或相似的优化结果[17]。本文三角梁性能分析分别采用单体模型和车身系统模型,计算模型并不相同,可以采用多模型优化方法,将拓扑域X作为共享设计变量,同步驱动单体模型和车身系统模型参与优化,优化流程及数学模型定义如图6所示。具体参与拓扑优化的工况参考表1,其中压铸三角梁碰撞等效静载工况采用压铸三角梁单体模型,为静态工况;其他工况采用车身系统超单元模型,扭转刚度、静刚度分析工况为静态工况,模态分析工况为动态工况。利用多模型拓扑优化方法,以静态、动态工况的综合目标函数f(ρ)最小为优化目标,以优化过程的设计域体积分数Vfrac(X)≤C(C为体积分数的目标值)作为优化约束,采用变密度法(solid isotropic material with penalization model, SIMP)[18]开展拓扑优化,在Optistruct软件环境下通过MATINIT=1.0命令定义迭代第0步的拓扑域单元密度为1,当取C=0.5,即体积分数Vfrac(X)≤0.5时,多次迭代收敛过程及最后一个迭代步的结果如图7所示。
最后一个迭代步往往包含最有效的优化信息,优化后单元密度接近1的区域视为关键传力路径。由图7b迭代收敛结果可以发现:拓扑域单元整体上向密度为0和1两端聚集,优化结果具有较好的离散性;区域①的单元密度均接近于1,说明此区域需要强化,在满足此区域螺栓安装功能的前提下,增强加强筋布置密度;区域②的关键传力路径从截面B的内侧边延伸到外侧边;区域③的关键传力路径与后横梁成约30°夹角;区域④由于压缩机悬置壳体嵌入横梁内部,导致局部区域薄弱,此处需要从悬置壳体发散出加强筋,
以提高局部区域刚度,确保三角梁模态、后横梁右悬置点Z向静刚度、截面C最大等效承载力;区域⑤关键传力路径与已有非设计域的侧边呈现整体贯通的特征;此外,为避让压缩机,前横梁悬置壳体区域较为薄弱,需要在悬置壳体附近增加加强筋,以增强前横梁整体刚度。
根据图7b的拓扑结构特征,在工程设计上保持区域①②⑤的设计对称性,完善加强筋结构设计数据,结果如图8所示。
3 基于组合代理模型的厚度优化
通过拓扑优化,完善了三角梁的结构设计,但具体结构的厚度需要合理定义,以实现轻量化。为便于三角梁厚度优化并保持模型仿真精度,悬置及端头安装位置设定为非设计域,采用体单元网格建模,需要厚度优化的结构对象采用壳单元网格建模,体网格与壳单元在搭接区采用共节点连接。
3.1 压铸结构厚度设计变量定义
三角梁下表面由多个“基面”组成,每个“基面”厚度均匀,可以设定为独立的设计变量;拔模方向的各加强筋和侧面统称为拔模面,由于拔模斜度要求使得拔模面根部较厚,拔出端较薄,故无法直接对拔模面的厚度进行参数化定义。本文采用厚度等效方法来实现拔模面厚度参数化定义,等效方法及步骤如下:
(1)在Hypermesh软件环境下,基于有限元模型选取任一壳单元,通过by face的方式选择相邻单元低于3°特征角度的所有单元,构建单独的零件组和属性组,并提取对应单元的体积和面积,则等效厚度由体积(Volume,用V表示)和面积(Area,用A表示)决定,等效厚度T(X)=V/A,属性信息中材料参数与原模型保持一致,厚度参数自动更新为等效厚度;
(2)三角梁结构中所有壳单元单独显示,通过二次开发程序对所有壳单元批量进行厚度等效,将三角梁结构中关于X=0平面完全对称的两组属性组合并为一个,将新构建的各属性组中的厚度参数定义为设计变量。
3.2 组合代理模型构造及精度校驗方法
代理模型通过建立输入与输出的映射关系,可有效降低仿真模拟的计算成本,因此在工程优化设计中得到广泛应用,相比于单一代理模型,组合代理模型具有更好的鲁棒性[19-20]。本文选取多项式响应面、径向基函数、Kriging函数参与组合模型构造,采用交叉验证(cross-validation, CV)精度校验方法获得各代理模型的精度评估值,根据精度评估值计算权重系数,通过线性加权确定组合代理模型,表达如下:
f^EN(x)=∑Mi=1wi(x)f^i(x)(8)
式中,M为参与构造组合代理模型f^EN(x)的单一代理模型f^i(x)的个数;wi(x)为权重系数。
CV采用均方根误差(root mean square error,RMSE)准则评估单一代理模型近似精度,表达如下:
eRMS,j=1Nt∑Ntj=1(fj(x)-f^j(x))2(9)
式中,fj(x)为样本点真实模型值;f^j(x)为代理模型值;Nt为检验代理模型精度的样本点个数。
本文权重系数计算仍然采用CV-RMSE准则,以权系数wi为设计变量,以均方根误差最小为目标函数,则组合代理模型计算过程转化为
find wi(x)
min eRMS,EN=1Ne∑Nek=1(fENk(x)-f^ENk(x))2
s.t. wi(x)≥0 ∑mi=1wi(x)=1(10)
式中,fENk(x)为样本点真实模型值;f^ENk(x)为组合代理模型值;Ne为检验组合代理模型精度的样本点个数。
3.3 设计优化
基于实验设计与代理模型开展压铸三角梁厚度优化,优化流程如图9所示,主要步骤描述如下。
(1)采用压铸三角梁各学科建模理论建立高精度分析模型,并对其求解精度进行校验,明确目标函数、约束条件、设计变量及设计空间等基本信息,构造优化模型。其中,分析模型包括采用车身系统超单元建模的车身扭转刚度分析模型、悬置点静刚度分析模型、模态分析模型,以及碰撞等效静载分析模型。
(2)采用实验设计方法在初始设计空间内获得无偏样本点,本文采用Maximin实验设计方法,具有设计空间内均匀分布的特征[21]。
(3)集成各分析模型,进行多样本求解,并提取设计变量与性能结果,获得初始(新增)样本点处的响应值。
(4)根据已有样本点的响应值,在当前设计空间内构造设计变量与性能之间的组合代理模型。
(5)校验组合代理模型的精度,如果精度满足要求,则基于组合代理模型进行优化,并将近似最优解作为优化结果输出;
否则,新增样本点并更新代理模型,直至满足精度要求。
(6)判断输出的优化结果是否满足工程需求。若满足则停止优化,将优化结果作为最优设计方案;否则需要转入步骤(1),调整优化模型并重新进行优化。
为满足结构设计与可制造性一体化,对步骤(1)中优化模型数学表达式施加制造约束,定义如下:
find x=(x1,x2,…,xn)
min f-(x)
s.t. gLBj≤g-j(x)≤gUBj j=1,2,…,M
Variable:xLB≤xa≤xb≤xUB
xi∈(xsp,[xLB,xUB])(11)
其中,f-(x)为设计变量的总质量;g-j(x)为基于代理模型的第j项性能;gLBj、gUBj分别为第j项性能目标的上下限值,目标值设定参考表1;xLB、xUB分别为设计变量的上下限,根据三角梁压铸工艺要求,设定xLB=2.2 mm、xUB=7 mm,且每隔0.4 mm离散取值;xa为远浇口设计变量厚度;xb为近浇口设计变量厚度,为保证压力压铸过程具有良好的模流性能,定义xa≤xb。为进一步识别并删除灵敏度较低的设计变量,额外将0.2 mm的离散厚度加入设计变量可取值范围,即拔模面厚度xsp=0.2 mm时,对应的结构可以考虑删除。
本文设计变量初始采样300个,构造组合代理模型,精度均高于99%,基于代理模型开展优化并迭代收敛,得到“基面”、拔模面的最优设计方案,删除厚度为0.2 mm的设计变量,厚度优化方案如图10所示。
将图10中等厚度的设计方案转化为变厚度的工程方案,各性能均采用有限元模型进行效果验证,性能结果如表4所示。由表4可以发现:①与厚度优化前对比,未达标性能如二阶弯曲模态、前横梁前悬置点静刚度、截面C最大等效静载力,经过厚度优化均达标,且减重0.1 kg;②与初始方案三角梁(表1)对比,厚度优化后的方案各性能得到不同程度的提高,其中二阶弯曲模态提高107.9 Hz,等效静载承载能力提高约60%,悬置点静刚度提高约30%,在满足性能目标基础上减重0.6 kg。
4 结论
(1)针对连续的车体结构提出子系统划分原则和方法,支撑进一步开展模型降阶。采用超单元模型开展单轮次分析,在保证分析精度前提下,车身系统模型缩减可节省97.3%的计算时间。
(2)针对一体压铸三角梁的结构设计问题,本文同步考虑压铸结构单体性能和车身系统性能,开展多模型拓扑优化完成加强筋设计;同步考虑设计与可制造性,对压铸结构变厚度拔模面进行参数化定义,并基于组合代理模型对各型面厚度进行参数设计。优化方法最大限度地兼顾性能与轻量化:相较于初始设计方案,二阶弯曲模态提高107.9 Hz,等效静载承载能力提高约60%,悬置点静刚度提高约30%,实现减重0.6 kg。
(3)本文的优化方法不仅考虑压铸三角梁的单体性能,还兼顾相关的系统级性能,并且优化结果满足压铸成形工艺要求,不仅适用于压铸三角梁结构,也适用于车身其他铸件的设计开发。
参考文献:
[1] 苏永雷,张志飞.副车架静刚度修正方法及多层级拓扑优化[J].汽车工程,2023,45(11):2157-2164.
SU Yonglei, ZHANG Zhifei. Correction Method of Static Stiffness and Multi-level Topology Optimization for Subframe[J]. Automotive Engineering, 2023,45(11):2157-2164.
[2] XU B, HAN Y S, ZHAO L, et al. Topology Optimization of Continuum Structures for Natural Frequencies Considering Casting Constraints[J]. Engineering Optimization, 2019, 51(6):941-960.
[3] ZHANG J Y, WANG S H, ZHAO H, et al. Manufacturable Casting Parts Design with Topology Optimization of Structural Assemblies[J]. Proceedings of the Institution of Mechanical Engineers, 2022, 236(4):401-412.
[4] WANG C, XU B, DUAN Z, et al. Structural Topology Optimization Considering both Performance and Manufacturability:Strength, Stiffness, and Connectivity[J]. Structural and Multidisciplinary Optimization, 2021, 63:1427-1453.
[5] 馬晶,亢战.一种基于附加重力场的铸件拓扑优化方法[J].计算力学学报,2021,38(4):498-504.
MA Jing, KANG Zhan. An Additional Gravity Field Method for Topology Optimization of Cast Parts[J]. Chinese Journal of Computational Mechanics, 2021,38(4):498-504.
[6] WANG Y, KANG Z. Structural Shape and Topology Optimization of Cast Parts Using Level Set Method[J].International Journal for Numerical Methods in Engineering,2017,111(13):1252-1273.
[7] 林佳武, 李玄霜, 陳宗明, 等. 真空高压铸造铝合金车身后纵梁轻量化设计[J]. 汽车工程, 2020, 42(3):383-389.
LIN Jiawu, LI Xuanshuang, CHEN Zongming, et al. Lightweight Design of Body Rear Longitudinal Beam of VAHP Die-casting Aluminum Alloy[J]. Automotive Engineering, 2020, 42(3):383-389.
[8] 雷飞, 韩旭,黄永辉.车身复杂结构大规模问题的缩减计算[J].中国机械工程,2009, 20(17):2127-2131.
LEI Fei, HAN Xu, HUANG Yonghui. Study on Reduced Methods in Solving Complex and Multi-parameterized Large Scale Problem in Automotive Body Design[J].China Mechanical Engineering,2009, 20(17):2127-2131.
[9] 雷飞, 韩旭. 基于分级自适应技术车身结构多参数大规模问题快速计算方法研究[J]. 中国机械工程, 2010, 21(6):668-671.
LEI Fei, HAN Xu. A Study of Rapid Evaluation for Structural Behavior of Multi-parameterized and Large-scale Problem in Vehicle Body Design[J]. China Mechanical Engineering, 2010, 21(6):668-671.
[10] 李昂, 刘初升.基于超单元技术的大型复杂结构的拓扑优化设计[J].中国机械工程, 2017, 28(20):2467-2474.
LI Ang,LIU Chusheng. Topology Optimization Designs of Large and Complex Structures Based on Super Element Technique[J]. China Mechanical Engineering,2017, 28(20):2467-2474.
[11] 王缅, 郑钢铁. 一种改进的固定界面模态综合法[J]. 宇航学报, 2012, 33(3):291-297.
WANG Mian, ZHENG Gangtie. An Improved Fixed Interface Modal Synthesis Method[J]. Journal of Astronautics, 2012, 33(3):291-297.
[12] 杜新欣, 张玮, 黄之文, 等.基于虚拟材料层和孪生有限元模型的机床主轴固定结合部动力学建模[J].振动与冲击, 2023, 42(9):11-18.
DU Xinxin, ZHANG Wei, HUANG Zhiwen, et al. Dynamic Modeling of Fixed Joint of Machine Tool Spindle Based on Virtual Material Layer and Twin Finite Element Model. Journal of Vibration and Shock, 2023, 42(9):11-18.
[13] TUREVSKY I, SURESH K. Efficient Generation of Pareto-optimal Topologies for Compliance Optimization[J]. International Journal for Numerical Methods in Engineering, 2011, 87(12):1207-1228.
[14] 胡启国, 周松. 考虑刚柔耦合的工业机器人多目标可靠性拓扑优化[J].计算机集成制造系统, 2020,26(3):623-631.
HU Qiguo, ZHOU Song. Multi-objective Reliability Topology Optimization Analysis of Rigid-flexible Coupling Industrial Robots[J]. Computer integrated Manufacturing Systems, 2020,26(3):623-631.
[15] 崔宇朋, 余杨, 韦明秀, 等. 改进博弈论四重组合赋权法下的开口甲板多目标拓扑优化设计[J]. 机械工程学报, 2023, 59(9):263-273.
CUI Yupeng, YU Yang, WEI Mingxiu, et al. Multi-objective Topology Optimization Design of Opening Decks Using Improved Fourfold Combination Weighting Model of Game Theory[J]. Journal of Mechanical Engineering, 2023, 59(9):263-273.
[16] SUBRAMANIAN N, RAMANATHAN R. A Review of Applications of Analytic Hierarchy Process in Operations Management[J]. International Journal of Production Economics, 2012, 138(2):215-241.
[17] JEONG M H, PARK G J. Nonlinear Dynamic Structural Optimization of Electric Vehicles Considering Multiple Safety Tests[J]. International Journal of Automotive Technology, 2023, 24(2):573-583.
[18] 董小虎, 王士涛, 周德淳. 光伏跟踪支架檩条结构高刚性轻量化设计[J]. 中国机械工程, 2023, 34(10):1207-1213.
DONG Xiaohu, WANG Shitao, ZHOU Dechun. High Rigidity and Lightweight Design of Purlins in Photovoltaic Tracker Bracket[J]. China Mechanical Engineering, 2023, 34(10):1207-1213.
[19] 李春明, 孙晓霞, 张涛, 等. 基于组合代理模型的变海拔工况车辆动力总成流动性能优化[J]. 机械工程学报, 2023, 59(4):135-144.
LI Chunming, SUN Xiaoxia, ZHANG Tao, et al. Optimization of Powertrain Mobility Performance of Vehicles with Variable Altitude Working Conditions by Ensemble of Surrogate Models[J]. Journal of Mechanical Engineering, 2023, 59(4):135-144.
[20] 刘基盛, 计良, 李威, 等. 基于多代理模型的离心叶轮高效优化设计方法[J]. 中国机械工程, 2023, 34(8):899-907.
LIU Jisheng, JI Liang, LI Wei, et al. Efficient Optimization Design Method of Centrifugal Impellers Based on Multi-surrogate Model[J]. China Mechanical Engineering, 2023, 34(8):899-907.
[21] MORRIS M D, MITCHELLT J. Exploratory Designs for Computational Experiments[J]. Journal of Statistical Planning and Inference, 1995, 43(3):381-402.
(編辑 袁兴玲)
作者简介:
苏永雷,男,1989年生,高级工程师、博士研究生。研究方向为结构分析与优化设计、汽车驾乘性能控制。E-mail:yongleisu@163.com。
张志飞(通信作者),男,1983年生,教授、博士研究生导师。研究方向为车辆结构分析与优化设计。E-mail:z.zhang@cqu.edu.cn。

