风车桥气动干扰作用下的汽车纵横向协调控制
袁志群 李曰瀚 林立 孙鹏飞 张义


摘要:
为提高跨海大桥上轿车的风致行车安全能力,采用合成风和动网格耦合方法建立了轿车超越集装箱货车的瞬态分析模型,揭示了“风车桥”气动交互作用机理及其对轿车气动特性的影响规律。采用五次多项式插值算法建立了超车轨迹规划模型,基于模糊逻辑的双PID控制方法与径向基神经网络的滑模控制方法设计了纵横向协调控制器,开展了轿车超车过程的路径跟踪能力分析及行驶稳定性评价。研究结果表明:风车桥的气动干扰大小与行驶车道及位置有显著关系,纵横向协调控制器的路径跟踪控制精度和鲁棒性较好,轿车侧风稳定性提高效果明显。
关键词:超车;气动干扰;侧风稳定性;路径跟踪;运动控制器
中图分类号:U461.1
DOI:10.3969/j.issn.1004132X.2024.04.016
开放科学(资源服务)标识码(OSID):
Longitudinal and Lateral Coordination Control of Cars with Aerodynamic
Interference of Wind-vehicle-bridge System
YUAN Zhiqun1,2,3 LI Yuehan1 LIN Li3 SUN Pengfei1,2 ZHANG Yi1,2
1.School of Mechanical and Automotive Engineering,Xiamen University of Technology,Xiamen,
Fujian,361024
2.Fujian Provincial Key Laboratory of Advanced Design and Manufacture for Bus Coach,Xiamen,
Fujian,361024
3.Fujian Provincial Key Laboratory of Wind Disaster and Wind Engineering,Xiamen,Fujian,361024
Abstract: To enhance the driving safety caused by cross-wind, the transient analysis model of a car overtaking truck on cross-sea bridge was established using a coupling method of composite wind and moving mesh, and the mechanism of aerodynamic interaction between “wind-vehicle-bridge” in the overtaking processes of a car and the influences on the aerodynamic characteristics of the car were revealed. The overtaking trajectory planning models were developed using a fifth degree polynomial interpolation algorithm, and the longitudinal and lateral coordination motion controllers were developed, using dual fuzzy PID control method for the longitudinal controllers and sliding mode control method of radial basis function network for the lateral controllers. The path tracking capability analysis and driving stability evaluation of the overtaking processes of a car under cross-wind were carried out. The results show that the aerodynamic interference is significantly related to the travelling lanes and positions. The longitudinal and lateral coordination motion controllers have better accuracy and robustness in controlling the path tracking, and the cross-wind stability is significantly improved.
Key words: overtaking; aerodynamic interference; cross-wind stability; path following; motion controller
收稿日期:20230828
基金項目:国家自然科学基金(52278537);福建省自然科学基金(2020J01275,2023J011435);福建省科技厅引导性项目(2021Y0045)
0 引言
跨海桥梁是城市交通体系的重要节点,桥上通行车辆的类型较多,自动驾驶汽车在未来交通出行中的占比将逐步提高,降低桥上的交通事故发生概率是提高桥梁通行效率的关键。诱发桥上交通事故的各因素中,风场的影响不可忽略,汽车、桥梁、侧风之间的相互干扰极为明显[1-3],国内外多座桥梁曾发生严重的风致行车安全事故,因此,开展汽车在“风车桥”气动交互干扰影响下的侧风稳定性及运动控制的研究对提高自动驾驶汽车的安全性具有重要的工程意义。
桥上汽车的风致行车安全研究与汽车侧风稳定性息息相关,国内外相关学者采用实车道路测试方法、风洞实验方法和汽车多体动力学分析方法对传统汽车进行了大量研究。其中,实车道路测试与实际情况最为接近[4],但测试成本高昂、研发周期较长,且无法进行极端工况的测试及验证,我国并未建设完善的侧风测试场景,特别是针对桥上行车的极限工况。风洞实验方法中的汽车一般为静止状态或直线运动状态,无法真实体现汽车控制器的反馈作用[5-6],与实际情况存在较大偏差。目前,汽车侧风稳定性研究主要采用汽车多体动力学方法开展开环分析[7-8]和客观评价,但相关研究并未以带有纵横向协调控制的自动驾驶汽车为研究对象。自动驾驶汽车通过轨迹跟踪和运动控制器来抵抗外界干扰,可有效控制汽车的侧向运动和横摆角运动。常见的运动控制方法包括滑模控制(sliding mode control,SMC)、模型预测控制(model predictive control,MPC)、线性二次最优控制(linear quadratic regulator,LQR)等方法[9-11],其中,滑模控制方法鲁棒性好,适用于不确定、抖动等复杂环境,适用于高速大转角工况,被广泛用于复杂环境下的运动控制[12]。但是相关研究并未开展真实侧风场景下的气动分析及横向控制,未能考虑汽车在实际行驶过程中行驶环境所引起的气动力和气动力矩变化,针对“风车桥”典型场景下的横向运动控制也鲜有研究,而该场景不仅是自动驾驶汽车在行驶过程中所面临的最为恶劣的行驶风环境,也是自动驾驶汽车进行极限工况测试与验证时必需考虑的问题。
针对上述问题,以跨海桥梁上轿车超越集装箱货车工况为研究对象,基于超车瞬态分析模型获取轿车分别在迎风侧和背风侧变道、加速以及并行阶段的气动力和气动力矩变化规律。设计纵横向协调控制器,纵向控制器以速度偏差与速度偏差变化率为输入,根据模糊论域及控制算法进行输出量的精准控制,实现PID参数的动态调整;横向控制器以横向误差、横向误差变化率、航向误差和航向误差变化率为输入,采用高斯基函数逼近系统误差与外部扰动,基于径向基神经网络结构设计外部干扰不确定项的控制输出量,提高车辆在匀速、变速状态下受到不同气动干扰后的控制精度和鲁棒性。研究结果不仅对提高桥梁风致行车安全能力具有较好的工程参考价值,还可为自动驾驶汽车在侧风干扰下的局部路径规划和运动控制提供理论参考。
1 数值计算模型
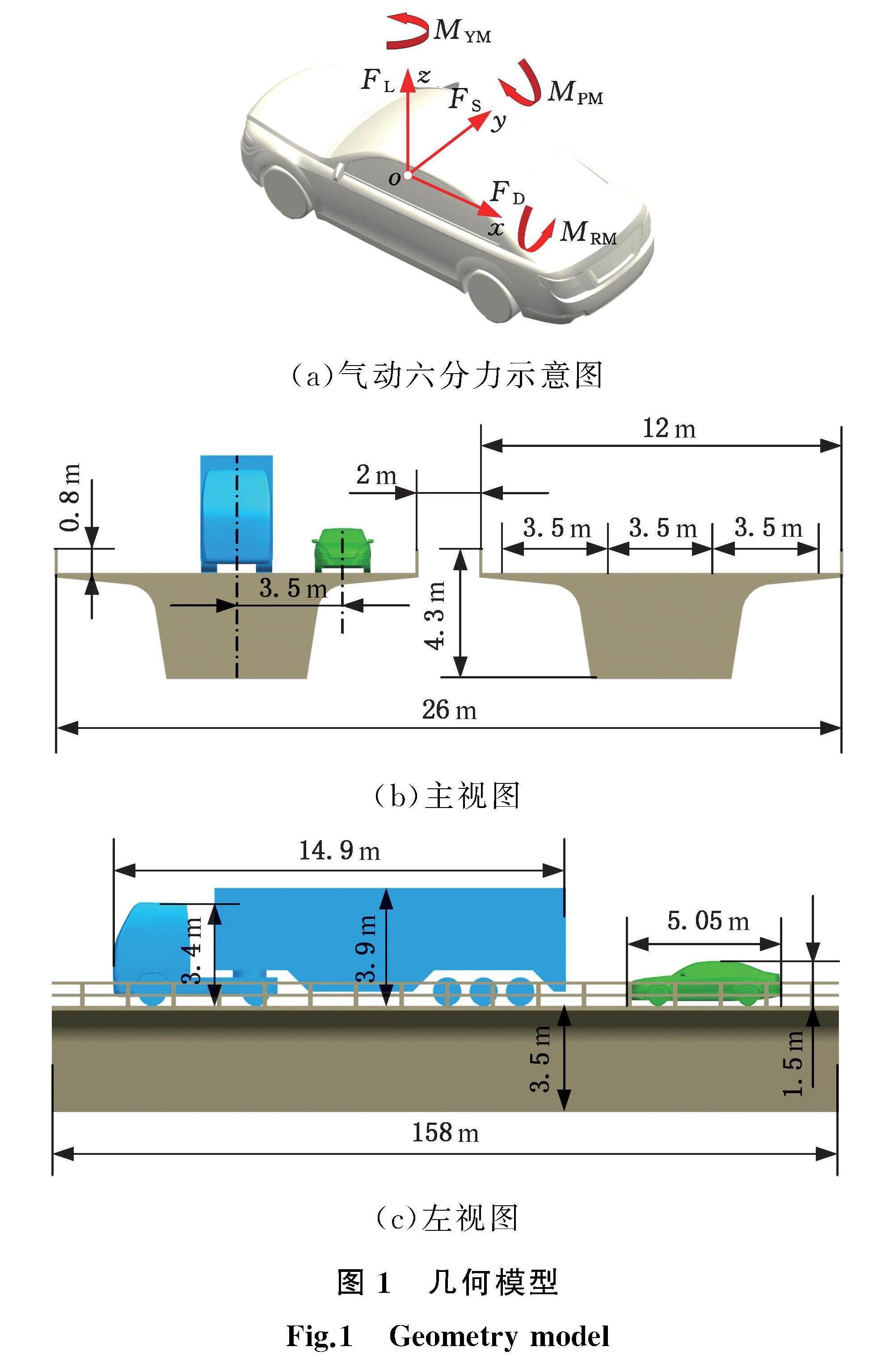
1.1 几何模型
本文主要开展桥上轿车超越集装箱货车行驶工况的侧风稳定性分析,分别建立轿车、集装箱货车以及双向六车道箱式桥梁的几何模型,如图1所示,其中,集装箱货车行驶在中间车道,轿车分别从左右两侧变道超车,空气动力学坐标系固定于轿车上,坐标系原点位于车辆轴距中心线和轮距中心线在地面上投影的交点。
1.2 计算方法及工况
被超货车在桥上的行驶速度为72 km/h,轿车在侧风作用下的超车过程分为变道阶段、加速阶段和并行阶段三段,如图2所示。轿车变道阶段的速度为72 km/h,变道时间为3 s;之后从72 km/h加速至108 km/h,加速时间为3 s,加速阶段末尾时刻的轿车车头距离集装箱货车车尾三倍轿车车长;并行阶段的速度为108 km/h,并行时间为4 s,并行阶段末尾时刻的轿车车尾距离集装箱货车车头一倍轿车车长。此外,轿车在变道之前以72 km/h行驶2 s、
在超车结束之后以108 km/h行驶6 s,该8 s行驶时间内均没有侧风的作用。
为了提高计算效率,对超车过程的气动数值计算模型进行一定简化,共设计5种气动计算工况以获取不同位置的轿车气动力和气动力矩,如图3所示,包括轿车分别在车道一、车道二、车道三单独行驶以及分别在车道一和车道三并行超越处于车道二的集装箱货车。其中,轿车在不同车道行驶工况的速度为72 km/h和108 km/h,轿车并行超车工况的速度为108 km/h,集装箱货车速度为72 km/h。忽略轿车匀速变道时车身姿态变化引起的气动力和气动力矩差异,对相应工况的气动力和气动力矩数据进行拟合处理。轿车并行超越集装箱货车的工况中,超车坐标系固定于被超车尾部,轿车前部与货车尾部的距离值根据轿车的长度l进行标准化,计算初始时刻轿车前部距离货车尾部三倍轿车车长,x标记为-3,计算结束时刻轿车尾部距离货车前部一倍轿车车长,x標记为5。
1.3 侧风计算模型
采用合成风及动网格耦合方法分别建立工况一~工况五的计算模型,计算域及相应的边界条件设置如图4a、图4b所示。其中,侧风加载方向与汽车行驶方向垂直,工况一~工况三入口速度ux为0,侧风风速uy分别设置为20 m/s和0,轿车行驶车速v分别设置为72 km/h和108 km/h,计算结果分别对应有侧风、无侧风(20 m/s或0)作用时轿车分别以72 km/h和108 km/h的速度行驶在跨海桥梁不同车道的情况;工况四和工况五入口速度ux为20 m/s(模拟被超货车速度72 km/h),侧风风速uy为20 m/s,轿车行驶速度v为相对车速36 km/h(模拟轿车与货车的相对速度),计算结果对应侧风风速为20 m/s时轿车在不同车道以108 km/h的车速并行超过以72 km/h行驶的集装箱货车。
车桥系统的几何形状极为复杂,因此,采用贴体性较好的四面体网格和三角形网格进行网格划分,如图4c所示。设置不同的网格加密方法和大小进行无关性验证,得到兼顾计算效率和计算精度的网格设置方案如下:轿车和货车全局面网格尺寸分别为16 mm和32 mm,局部细节的面网格为4 mm,车体周围设置了3层加密区,体网格尺寸分别为64 mm、128 mm和512 mm,其中,车身表面共生成6层高度逐渐递增的棱柱层网格,计算结果满足y+值要求,计算域体网格总量为4400万左右。计算求解方法采用可实现k-ε湍流模型、基于压力耦合的半隐式算法以及二阶迎风离散格式,该算法已在汽车空气动力学中广泛应用[3,8,13]。
2 合成风与动网格耦合计算方法验证
参考湖南大学风洞实验室的测试数据验证本文数值计算方法的准确性,采用上述网格划分方案和边界条件设置方法建立与风洞实验工况对应的计算模型,如图5所示。风洞实验采用的轿车模型比例为1∶3,实验来流风速为30 m/s,横摆角β为15°,数值计算时侧风加载速度ux为0,uy=vy,设置为7.765 m/s,轿车的运动采用动网格模拟,车速v=vx,设置为28.978 m/s,速度分解方法如图5b所示。数值模拟与风洞实验满足几何相似、雷诺相似、运动相似,数值模拟与风洞实验结果较为接近,如图5a所示,说明本文侧风计算模型的模拟精度达到工程应用要求。
3 轿车变道和加速阶段的气动分析
图6为轿车单独行驶时yz截面的速度云图,可以看出,桥梁及防撞护栏产生的绕流对桥面风场影响较大。距桥面越高的位置,风速越大;近地面风速明显小于来流风速;迎风侧桥上,车道离迎风侧越远,轿车迎风侧风速明显越低。当风速为20 m/s时,
近地面2 m高度内车道一~车道三的等效风速分别为13.6 m/s、6.5 m/s、4.7 m/s,近地面4.5 m高度内车道一~车道三的等效风速分别为21.9 m/s、20.0 m/s、18.7 m/s。
桥面风速的差异使得不同工况的气动力存在明显差异,本文以对侧风稳定影响较大的气动侧力和气动横摆力矩为对象进行分析,如图7所示。轿车在车道一行驶时的气动侧力和气动横摆力矩最大,而在车道三行驶时最小。轿车以72 km/h的速度由第二车道变道到第一车道后,气动侧力增大135.4 N,气动横摆力矩增大396.4 N·m,而由第二车道变道到第三车道后,气动侧力减小17.4 N,气动横摆力矩减小40.3 N·m。轿车在车道一由72 km/h加速至108 km/h时,气动侧力增大271.4 N,气动横摆力矩增大180.1 N·m,而在车道三加速时,气动侧力增大206.3 N,气动横摆力矩增大83.8 N·m。
4 轿车并行阶段的气动分析
轿车超越货车时,两车的流场干扰较为明显,如图8所示。货车尾部迎风侧出现明显的气流加速区,呈高速低压特点,而尾部和中部背风侧则出现明显的气流屏蔽区,呈低速低压特点,货车尾流区对另一幅桥梁的影响不可忽略。轿车在第一车道接近货车时,迎风侧风速逐渐增加,与货车并行过程中,受货车遮挡,迎风侧风速逐渐减小,超越货车后又逐渐增加直至稳定。在第三车道接近货车时,轿车逐渐进入货车尾部的尾流区,迎风侧风速逐渐减小,超越货车后逐渐趋于稳定。流场差异导致气动侧力和气动横摆力矩呈现完全相反的变化趋势,如图9所示。
轿车在第一车道超车时,气动侧力和气动横摆力矩呈先增大、后减小、再增大的趋势,气动侧力变化范围为-1480~-274 N,气动横摆力矩变化范围为411~1438 N·m;轿车在第三车道超车时,气动侧力和气动横摆力矩呈先减小、后增大、再减小的趋势,气动侧力变化范围为-1273~240 N,气动横摆力矩变化范围为34~1202 N·m。与迎风侧车道超车相比,轿车在背风侧超车的气动侧力和气动横摆力矩峰值分别减小13.9%和16.4%,变化幅度分别增加25.5%和13.7%。
进一步分析发现,轿车在背风侧超车时,货车的遮挡削弱了侧风作用,气动侧力出现了明显的降幅,但货车尾部负压区和前部正压区会导致轿车的气动侧力和气动横摆力矩变化幅度更大;而在第一车道超车时,迎风侧风速更高,且货车尾部迎风侧的高速低压区所形成的吸力会进一步恶化轿车的气动特性,因此,其气动侧力和气动横摆力矩比第三车道的大。
5 轿车超车过程的侧风稳定性分析
5.1 纵横向协调控制方法
在MATLAB、Simulink和CarSim软件中搭建轿车超车过程的纵横向协调控制模型,如图10所示。首先,基于五次多项式插值算法建立轿车超车过程的变道轨迹,该算法不仅具有高拟合精度,还可避免轨迹振荡;其次,基于模糊控制算法建立纵向速度和位移的双PID纵向控制器;最后,基于径向基神经网络(radial basis function,RBF)建立双滑模面横向控制器,通过在跟踪误差模型中引入不确定项来减小建模误差,提高滑模控制器在侧风工况下的鲁棒性与跟踪精度。
5.2 轨迹规划模型
轿车在背风侧超车的轨迹规划模型如图11所示,轿车在迎风侧超车的轨迹规划模型同理可得。在无侧风作用的前2 s为匀速直线行驶,纵向速度vp為20 m/s,纵向加速度ap、航向角θr和曲率kr均为0,横向位置y为0,纵向位置x为20t。变道过程任意时刻的横向位置y(t)和纵向位置x(t)如下:
x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
y(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5(1)
分别对横向、纵向位置方程求导得到速度方程和加速度方程,由图11中关系可知,变道的起点和终点需满足如下约束条件:
x(t2)=40 m x·(t2)=20 m/s x¨(t2)=0
x(t5)=100 m x·(t5)=20 m/s x¨(t5)=0
y(t2)=0 y·(t2)=0 y¨(t2)=0
y(t5)=3.5 m y·(t5)=0 y¨(t5)=0(2)
联立式(1)和式(2)可求得系数a0~a5和b0~b5,由此可确定变道轨迹方程,其中,变道规划轨迹的航向角θr、曲率kr、纵向速度vp、纵向加速度ap以及纵横向x、y位置关系满足如下计算式:
θr=arctan(y′(x(t)))
kr=y″(x)/(1+(y′(x))2)32(3)
y′(x)=x·(t)/y·(t)
y″(x)=y¨(t)x·(t)-x¨(t)y·(t)(x·(t))3(4)
vp=x·(t)2+y·(t)2
ap=x¨(t)2+y¨(t)2(5)
轿车在加速和超车过程的轨迹为直线,航向角θr和曲率kr均为0,横向位置y坐标为3.5 m,则纵向速度vp、纵向加速度ap以及纵向位置x满足:
ap=(vt8-vt5)/(t8-t5)=10/3
vp=vt5+ax(t-5)=20+ax(t-5)
x=100+20(t-5)+0.5ax(t-5)2(6)
ap=0vp=30x=175+30(t-8)(7)
5.3 基于模糊逻辑的PID纵向控制模型
纵向速度和位移采用双PID控制方法进行轨迹跟踪,纵向位移PID控制器是以期望纵向位移xr(t)与车辆实际位移x(t)的误差ex作为控制输入量,纵向速度模糊PID控制器是以期望纵向速度vr(t)与实际的纵向速度vx(t)误差ev及其变化率作为控制输入,加速度控制量a和偏差输入量e的计算表达式为
a(t)=K*pe(t)+K*i∫t0e(t)dt+K*dde(t)dt(8)
ex(t)=xr(t)-x(t)ev(t)=vr(t)-vx(t) (9)
K*p=Kp+ΔKpK*i=Ki+ΔKiK*d=Kd+ΔKd(10)
式中,Kp、Ki、Kd为系统输入的初始值,分别为比例项系数、积分项系数和微分项系数;ΔKp、ΔKi、ΔKd为基于模糊推理后得到的控制参数修正量。
最终得到理想的期望加速度ax,并结合当前的车辆实际速度vx以及逆纵向动力学模型获得油门开度α或制动压力p,其中,逆纵向动力学模型根据仿真实验法进行速度、加速度、油门开度以及速度、减速度、制动系数的数据标定,如图12所示。
模糊变量的输入参数包括纵向速度误差ev及其变化率,输入变量的模糊论域分别为[-0.3,0.4]和[-4,3],模糊输出变量ΔKp、ΔKi、ΔKd的模糊论域分别为[-0.1,0.1]、[0,0.5]、[0,0.06],将模糊论域分为7个部分,表示为负大、负中、负小、零、正小、正中及正大,根据以下原则进行自变量整定并设定模糊控制表。
(1)纵向速度误差ev小于0的条件下,车辆实际速度大于预期车速。ev的变化率小于0时,汽车处于减速状态,此时应增大比例环节,减小微分环节。
(2)纵向速度误差ev大于0的条件下,车辆实际速度小于预期速度。ev的变化率大于0时,汽车处于加速度状态,可以适当减小比例环节,采取微分环节进行提前调节;ev的变化率小于0时,车辆处于减速状态,一般属于曲线振荡的阶段,ev及其变化率较小时,选择较小的ΔKd。
5.4 基于RBF的滑模面横向控制模型
横向控制以二自由度动力学模型为参考,如图13所示,采用滑模控制方法进行轨迹跟踪,该控制策略具有较好的鲁棒性,满足文中工况的汽车性能需求。基于二自由度动力学模型建立轿车运动空间状态方程,作为轿车在侧风作用下侧偏运动和横摆运动的参考模型。当轮胎侧偏角较小时,其动力学微分方程的简化形式如下:
m(v·y+vxφ·)=Ffcos δ+Fr
Izφ¨=aFfcos δ-bFr
Ff=Cafα1
Fr=Carα2(11)
式中,m为汽车质量;vx、vy分别为汽车质心的纵向速度和侧向速度;φ为横摆角;Ff、Fr分别为前后轮的侧偏力;δ为前轮转角;Iz为汽车横摆惯量;a、b分别为汽车质心到前后轴的距离;Caf、Car分别为前后轮侧偏刚度;α1、α2分别为前后轮侧偏角。
由路径跟踪误差模型的运动学分析可得运动学关系:
vy=e·y-vxeφv·y=e¨y-vxe·φφ·=e·φ+θ·rφ¨=e¨φ(12)
代入二自由度动力学参考模型,以横向误差、横向速度误差、航向误差和横摆角速度误差作为状态量,根据期望轨迹的参数信息建立轿车超车过程的跟踪误差模型,如图13所示,其状态空间方程为
X·=AX+Bδ+Cθ·r(13)
A=
0100
0
2Caf+2Carmvx-
2Caf+2Carm
2Cafa-2Carbmvx
0001
02Cafa-2CarbIzvx
2Carb-2CafaIz
2Cafa2+2Carb2Izvx
B=0-2Cafm0-2CafaIz
C=02(Cafa-Carb)mvx-vx0
2(Cafa2+Carb2)vxIz
X=eye·y
eφe·φ
由式(13)軌迹跟踪误差模型可知,通过控制前轮转角很难同时满足横向误差和航向误差要求,因此,本文基于滑模控制理论设计横向和航向双滑模面函数S1和S2,建立两组误差子系统的状态向量横向控制器:
S1=c1ey+e·y
S2=c2eφ+e·φ→S=cS1+(1-c)S2(14)
式中,c1、c2分别为横向误差子系统滑模面S1的控制系数、航向误差子系统滑模面S2的控制系数;c为总滑模面S的控制系数。
为保证系统趋于滑模面运动,基于等效滑模控制方法设计由等效控制项ueq和切换控制项ur组成的滑模控制率。
当系统运动到滑模面时需满足如下条件:
S·=c(c1e·y+e¨y)+(1-c)(c2e·φ+e¨φ)=0(15)
推导得到等效控制量:
ueq=-c(c1e·y+M)-(1-c)(c2e·φ+N)(1-c)B4+cB2(16)
M=2Caf+2Carmvxe·y-2Caf+2Carmeφ+
2Cafa-2Carbmvxe·φ+(2Caf-2Carmvx-vx)θ·r
N=2Cafa-2CarbIzvxe·y+2Carb-2CafaIzeφ+
2Cafa2+2Carb2Izvxe·φ+2Cafa2+2Carb2Izvxθ·r
B2=-2Caf/m B4=-2Cafa/Iz
當系统状态未达到滑模面时,为了降低系统的抖振问题,基于指数趋近率和双曲正切函数设计切换控制项:
ur=-εtanh(S)-kS(1-c)B4+cB2(17)
式中,k为指数趋近律中的指数项系数;ε为等速趋近项系数。
最终得到横向控制时的前轮转角控制量:
δ=ueq+ur(18)
车辆轨迹跟踪误差方程中,侧向速度变化率与横摆角速度变化率可以简写为
e¨y=M+B2ue¨φ=N+B4u(19)
汽车是一个非线性系统,在侧风环境下超车时,汽车自身参数与外界的干扰是不断变化的,传统的滑模控制方法难以保证侧风工况下超车时的横向轨迹跟踪精度,因此,将上述汽车自身参数与外部扰动变化对汽车的影响归结于横向与航向角的干扰,车辆轨迹跟踪误差模型可表述为
e¨y=B2u+d1e¨φ=B4u+d2(20)
对包含不确定项的系统设计滑模控制律,设计过程同上文所述,最后得到的总控制律如下:
δ=-c(c1e·y+d1)-(1-c)(c2e·φ+d2)(1-c)B4+cB2+
-kS-εtanh(S)(1-c)B4+cB2(21)
采用4-5-1结构形式的RBF神经网络对控制律中的不确定项d1和d2进行逼近预估,以横向误差、横向误差变化率、航向误差、航向误差变化率为RBF神经网络的输入向量,以高斯基函数作为隐含层的径向基函数,网络输出为模型预估的不确定项,图14所示为滑模面控制的神经网络结构。隐含层高斯基函数与网络输出估计值计算式如下:
hj=exp(-‖x-cj‖22b2j) j=1,2,3,4,5(22)
d^1=W^h1(x)
d^2=U^h2(x)(23)
式中,x为网络的输入;cj为第j个节点的中心值向量;bj为第j个节点的高斯基函数基宽值;h(x)为高斯基函数的输出,h(x)=[h1 h2 h3 h4 h5]T;W^、U^为神经网络自适应权值。
mode control
联立式(15)、式(20)、式(21)、式(23)求解得到
S·=cW~Th1(x)+(1-c)U~Th2(x)-kS-εtanh(S)(24)
式中,W~、U~为神经网络权值的估计误差。
利用Lyapunov函数稳定性分析方法设计网络权值自适应律并保证系统的稳定性,定义Lyapunov函数为
L=12S2+12η1W~TW~+12η2U~TU~(25)
对其求导得
L·=SS·+1η1W~TW·~+1η2U~TU·~=
(ch1(x)S-1η1W·~)W~T+[(1-c)h2(x)S-
1η2U·~]U~T-kS2-ε|ε|(26)
式中,η1、η2为网络权值自适应律中的自适应系数。
设计自适应计算式为
W·~=cη1Sh1(x)
U·~=(1-c)η2Sh2(x)(27)
当ε>0、k>0时,满足L·≤0,根据Lyapunov稳定性定理证明可知,系统存在模型误差及外界干扰时,轨迹跟踪误差将全局渐进收敛至零,因此,将带有不确定项的滑模控制律表示为等效控制项与切换控制项之和,车辆横向运动控制中的前轮转角可表示为
δ=-c(c1e·y+d^1)-(1-c)(c2e·φ+d^2)(1-c)B4+cB2+
-kS-εtanh(S)(1-c)B4+cB2(28)
5.5 轿车超车过程的侧风稳定性分析
图15和图16所示为轿车超越货车过程的动力学响应及横向控制效果,其差异主要体现如下。
(1)变道阶段。侧向加速度、侧向速度和横摆角速度均呈现相同变化趋势,变化较为平缓,侧向加速度在合理范围内,轿车不会发生侧滑。变道到车道一过程有、无RBF的滑模控制器时,侧向速度峰值分别为0.45 km/h和0.44 km/h,横摆角速度峰值分别为6.63°/s和6.64°/s,变道到车道三时的侧向速度峰值分别为0.39 km/h和0.39 km/h,横摆角速度峰值分别为6.59°/s和6.44°/s。变道过程中有无RBF滑模控制器的动力学差异不明显,变道到车道一时略大,原因在于该阶段侧风引起的气动干扰较小,轿车变道到不同车道时的气动力和气动力矩较为接近。
(2)加速阶段。侧向速度均逐渐增大,轿车在车道三结束时刻的侧向速度为0.27 km/h,而在车道一加速时为0.05 km/h,受集装箱货车尾部迎风侧加速气流的影响,车道一加速过程的气动横摆力矩远大于车道三同位置车辆,RBF滑模控制器预测较大的侧向风干扰并及时补偿前轮转角,而相对影响较小的车道三补偿较少,其相应时段的前轮转角较小,因此轿车在车道三的侧向速度略大于车道一同位置的轿车。之后轿车逐渐接近集装箱货车,
超车过程的侧向速度呈不规则的波动,且呈现相反的变化趋势,而加速和超车过程的横摆角速度变化相比速度变化更小。
(3)并行阶段。轿车在车道一并行时,RBF滑模控制器下的侧向加速度、横摆角速度和侧向速度峰值分别为0.046g、1.00°/s、0.36 km/h,无RBF滑模控制器下相应值分别为0.051g、1.54°/s、0.43 km/h,相较于无RBF滑模控制器时分别提高了9.8%、35.1%、16.3%。峰值出现在超车阶段的8.0~9.5 s内,该时段内的气动侧力与气动横摆力矩数值整体上均远大于车道三处的同位置车辆,而随后车道三的气动侧力与气动横摆力矩逐渐超过车道一,但气动力与气动力矩变化幅值不大且变化较快,因此,轿车在车道三超车时有无RBF滑模控制器下的动力学响应参数区别不大,但峰值均大于车道一同位置下的响应参数。第三车道并行时,侧向加速度、侧向速度和横摆角速度的波动频率更快,出现较多拐点,这对乘坐舒适性有不利影响。
由图15d可知,风车桥强烈的气动交互干扰造成前轮转角出现了一定幅度波动,车道一超车过程的波动幅度更高。变道阶段,前轮转角变化较为平缓,车道一和车道三超车时前轮转角的平均控制量分别为0.15°和0.07°,峰值分别为1.12°和1.06°;加速阶段,前轮转角的平均控制量分别为0.45°和0.19°,峰值分别为0.78°和0.40°;并行阶段,前轮转角的平均控制量分别为0.39°和0.20°,峰值分别为0.81°和0.39°。
由图16a和图16b可知,轿车在车道一超车时,变道、加速以及并行阶段的横向误差最大值分别为17.1 mm、10.5 mm、14.6 mm,航向误差最大值分别为0.26°、0.15°、0.21°;而轿车在车道三超车时,横向误差最大值分别为14.8 mm、7.3 mm、7.6 mm,航向误差最大值分别为0.24°、0.12°、0.17°。RBF滑模控制器对提高横向误差效果显著,在车道一变道、加速以及并行阶段的横向误差分别减小了9.2 mm、9.5 mm、13.6 mm,车道三横向误差分别减小了9.4 mm、6.8 mm、7.0 mm。
由图16c可以看出,模糊逻辑PID控制器对纵向速度的跟蹤精度明显提高,并行阶段的初始时刻,受集装箱货车尾部气流与车辆加速时惯性的影响,速度出现了一定的超调量,轿车在车道一行驶时,有无模糊逻辑控制的速度峰值分别为108.81 km/h与109.42 km/h,在车道三处速度峰值分别为108.84 km/h与109.20 km/h,相较于无模糊逻辑PID控制器,轿车在车道一、三的速度峰值分别减少了0.61 km/h与0.36 km/h。受超车过程气动干扰的影响,轿车在模糊逻辑PID控制器的调节下,在车道一、三分别经历1.8 s和1.6 s的并行行驶后速度趋于稳定并达到期望速度,速度误差基本为0,而无模糊逻辑PID控制器下分别需经历2.4 s和2.2 s才能进入稳定阶段,但之后仍以0.18 km/h的误差幅度上下波动。
为了验证本文RBF滑模控制器(RBF-SMC)在侧风超车工况下的有效性,将其与常用的模型预测控制(MPC)方法、线性二次最优控制(LQR)方法进行对比,如图17所示。车道一超车时,MPC方法在变道、加速以及并行阶段的最大横向误差分别为42.9 mm、38.2 mm、49.5 mm,LQR方法的最大横向误差分别为81.8 mm、57.6 mm、9.7 mm;轿车在车道三超车时,MPC方法在变道、加速以及并行阶段的最大横向误差分别为35.6 mm、18.1 mm、36.5 mm,LQR方法的最大横向误差分别为81.2 mm、57.7 mm、6.5 mm。相较于MPC方法,RBF-SMC方法在变道、加速以及并行阶段均有更好的表现。相较于LQR方法,RBF-SMC方法的优异性主要体现在变道和加速阶段。
综上,本文设计的纵横向协调控制器能很好地进行轨迹跟踪,侧风作用下的变道过程、加速过程、并行过程的横向误差、航向误差和速度误差无较大变化,不同侧向干扰下的控制效果较为稳定且具有较好的鲁棒性。与传统的汽车运动控制方法相比[14-15],侧向位移得到了明显改善,自动驾驶汽车的风致行车安全能力得到显著提高。
6 结论
(1)迎风侧超车时,轿车的气动侧力和气动横摆力矩极值更大,动力学响应的峰值更高,对风致安全影响较大;背风侧超车时,轿车的气动侧力和气动横摆力矩变化幅度更大,动力学响应的变化频率更快,对风致舒适性影响更明显。
(2)基于径向基神经网络的滑模控制器可较好地控制风车桥的气动干扰,横向误差在17.1 mm以内,航向误差在0.26°以内,与常用控制方法相比,侧风稳定性提高效果明显。
(3)基于模糊逻辑PID控制器的速度跟踪效果较好,误差在1.36 km/h以内,并行阶段的车速变化更为平稳,在迎风侧和背风侧车道上达到稳定期望速度的时间缩短了25.0%与27.3%。
参考文献:
[1] ZHANG M J, ZHANG J X, LONG J T, et al. CFD Numerical Simulation of Wind Field and Vehicle Aerodynamic Characteristics on Truss Bridge Deck under Crosswind[J]. KSCE Journal of Civil Engineering, 2022, 26(12):5146-5159.
[2] WANG B, XU Y L. Safety Analysis of a Road Vehicle Passing by a Bridge Tower under Crosswinds[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2015, 137:25-36.
[3] 袁志群,刘宇峰,林立.强风环境下跨海桥梁行车安全评价与管控方法[J].汽车工程,2022,44(9):1456-1467.
YUAN Zhiqun, LIU Yufeng, LIN Li. Evaluation and Management Method of Vehicle Driving Safety on Cross-sea Bridge under Strong Wind Environment[J]. Automotive Engineering, 2022, 44(9):1456-1467.
[4] KEE J D, RHO J H, KIM K H, et al. High Speed Driving Stability of Passenger Car under Crosswind Effects[J].International Journal of Automotive Technology, 2014, 15(5):741-747.
[5] CHEN N, SUN H X, WANG X Y, et al. The Aerodynamic Characteristics of Road Vehicles Overtaking on Bridge Deck under Crosswinds[J]. Advances in Civil Engineering, 2020, 2020:1-12.
[6] CHEN N, WANG X Q, LI S K, et al. Safety Analysis of Road Vehicles Overtake on Cables-stayed Bridge under Crosswinds[J]. Advances in Structural Engineering, 2023, 26(5):870-887.
[7] 李舒雅,谷正气,黄泰明,等.不同侧风工况下汽车稳定性双向耦合研究[J].中国机械工程,2019,30(19):2276-2286.
LI Shuya, GU Zhengqi, HUANG Taiming, et al. Two-way Coupling Analysis of Vehicle Stability in Different Crosswind Conditions[J]. China Mechanical Engineering, 2019, 30(19):2276-2286.
[8] SU C Q, HU Z, ZHANG Q W, et al. Coupling Analysis of Transient Aerodynamic and Dynamic Response of Cars in Overtaking under Crosswinds[J]. Engineering Applications of Computational Fluid Mechanics, 2020, 14(1):1215-1227.
[9] 胡杰,钟鑫凯,陈瑞楠,等.基于模糊LQR的智能汽车路径跟踪控制[J].汽车工程,2022,44(1):17-25.
HU Jie, ZHONG Xinkai, CHEN Ruinan, et al. Path Tracking Control of Intelligent Vehicles Based on Fuzzy LQR[J]. Automotive Engineering, 2022, 44(1):17-25.
[10] 张志达,郑玲,张紫微,等.基于自适应模型预测的智能汽车横向轨迹跟踪控制[J].中国公路学报,2022,35(7):305-316.
ZHANG Zhida, ZHENG Lin, ZHANG Ziwei, et al. Lateral Trajectory Tracking Control of Intelligent Vehicles Based on Adaptive Model Prediction[J]. China Journal of Highway and Transport, 2022, 35(7):305-316.
[11] 蔡英凤,李健,孙晓强,等.智能汽车路径跟踪混合控制策略研究[J].中国机械工程,2020,31(3):289-298.
CAI Yingfeng, LI Jian, SUN Xiaoqiang, et al. Research on Hybrid Control Strategy for Intelligent Vehicle Path Tracking[J]. China Mechanical Engineering, 2020, 31(3):289-298.
[12] TAGHAVIFAR H .Integrated Control of Vehicle Stability by Nonlinear Observer-based Exponential-like Sliding Mode Neural Network System[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2021, 235(14):3474-3486.
[13] 梁寶钰,汪怡平,刘珣,等.基于滑模理论的高速车辆侧风稳定性控制研究[J].汽车工程,2022,44(1):123-130.
LIANG Baoyu, WANG Yiping, LIU Xun, et al. Study on Crosswind Stability Control of High-speed Vehicle Based on Sliding Mode Theory[J]. Automotive Engineering, 2022, 44(1):123-130.
[14] 丁能根,康乐,王健,等.侧向风干扰下的汽车主动前轮转向最优控制[J].北京工业大学学报,2013,39(2):161-165.
DING Nenggen, KANG Le, WANG Jian, et al. Optimal Control of Active Front Wheel Steering for Vehicles under Perturbation of Crosswind[J]. Journal of Beijing University of Technology, 2013, 39(2):161-165.
[15] 陈丰,彭浩荣,马小翔,等.侧风作用下货车驾驶员反应行为模型[J].同济大学学报(自然科学版),2020,48(5):702-709.
CHEN Feng, PENG Haorong, MA Xiaoxiang, et al. Model of Driving Behavior of Truck Driver under Crosswind[J]. Journal of Tongji University (Natural Science), 2020, 48(5):702-709.
(编辑 袁兴玲)
作者简介:
袁志群,男,1983年生,副教授。研究方向为汽车系统动力学及控制。发表论文30余篇。获发明专利10余项。E-mail:yzqhnu@163.com。

