基于动态CRITIC赋权的中国金融压力指数构建与金融风险识别
祝志川 蒋犇

摘要:合理测度和准确识别金融市场风险,对于稳定经济、有效防范金融风险意义重大。依据中国金融市场特征,本文采用动态CRITIC法计算权重并建立金融压力指数测度模型,通过非参数统计核密度法和B-N数据分解法对金融压力指数的分布和金融风险状态进行估计与识别,采用马尔科夫区制转换模型检验高低风险转换概率,并与基于确定项进行识别的结果进行对比分析。研究表明:基于动态CRITIC赋权的金融压力指数更能反映金融市场的极端值和金融风险,随机冲击是影响我国金融压力指数的重要因素,两种金融风险识别方法均可识别金融风险状态且各有优势,研究中可以互为补充。今后应建立更加完善的风险测度指标体系,进一步完善监管制度,加强对金融风险的宏观审慎管理和防范。
关键词:金融压力指数;动态CRITIC法;B-N数据分解法;马尔科夫区制转换模型
中图分类号:F832 文献标志码:A 文章编号:1007-8576(2024)01-0021-13
DOI:10.16716/j.cnki.65-1030/f.2024.01.003
Construction and Application of China's Financial Stress Index
Based on Dynamic CRITIC Weighting Method
and Financial Risk Identification
ZHU Zhichuan, JIANG Ben
(Liaoning University, Shenyang 110036, China)
Abstract: Reasonable measurement and accurate identification of financial market risks are of great significance for stabilizing the economy and effectively preventing financial risks. According to the characteristics of China's financial market, this paper uses the dynamic CRITIC method to establish the measurement model to calculate the financial stress index, and estimates and identifies the distribution and risk state of financial stress index through non-parametric statistical kernel density method and B-N data decomposition method and the Markov Regime Switching Model is used to test the high and low risk transformation probability of financial stress index to compare with the results identified by deterministic items. The research results indicate that the financial pressure index based on dynamic CRITIC weighting method can better reflect the extreme values and financial risks of the financial market. Random shocks are an important factor affecting China's financial pressure index, and both financial risk identification methods can identify the financial risk status and each has its own advantages. In the future, it is of great necessity to establish a more complete risk measurement index system, further improve the regulatory system, and strengthen macro-prudential management and prevention of financial risks.
Key words: financial stress index; dynamic CRITIC method; B-N data decomposition method; Markov regime switching model
一、问题的提出
金融是现代市场经济的核心,是实现经济高质量发展的重要推动力量,金融市场稳定是市场经济长期健康发展的必然要求。2021年一季度,我国宏观杠杆率为276.8%,非金融企业部门杠杆率为160.3%,政府部门杠杆率为44.5%,住户部门杠杆率为72.1%1,这可从某种角度说明我国实体经济风险处于较高水平,实体经济在金融市场的投融资活动引致了较高的杠杆率,对金融市场带来了巨大隐患。同时,不同国家和地区的金融市场之间存在较强的相关性,在对外开放广度和深度不断扩大的背景下,中国同世界各国之间的经济联系日益密切,金融风险随资本活动在全球经济体间传导,影响金融风险的因素从内部延伸到外部,风险传导的复杂性和多渠道性增强。因此,科学测度金融市场压力,把握金融市场压力变动规律,采用科学方法准确识别金融风险及风险状态转换,这对宏观调控金融市场、防范金融风险、促进经济高质量发展具有重要的理論意义和实践价值。
金融压力指数具有覆盖范围广、时效性强的特点,在研究金融风险时被广泛使用。Illing[1]利用因子分析、信用权重等方法测度了加拿大的金融压力指数。Hakkio[2]构建了堪萨斯城金融压力指数,并用该指数分析1999—2009年间的金融危机时期,研究表明该指数的峰值能够与危机时期发生的极端金融事件相对应,从而从实证角度证明了金融压力指数能够描述金融风险极值。Balakrishnan[3]测度了新兴经济体的金融压力指数,研究了金融压力从发达经济体向新兴经济体的传导过程。Ozcelebi[4]研究了发达国家金融压力指数对其他国家的影响,发现发达国家会利用经济优势,将大部分压力传导到新兴经济体。Cevik[5]关于金融压力指数与经济活动之间关系的研究表明,金融压力指数对宏观经济变化有很大影响,金融压力指数能够预示经济状况。王维国[6]构建了反映货币、银行和资产价格风险的压力指数,利用區制转移向量自回归模型对3类压力指数进行了识别。Macdonald[7]利用金融压力指数研究了不同国家的金融稳定情况,发现金融市场存在较强的依赖性和风险溢出性。丁岚[8]利用由动态权重合成的中国金融压力指数进行的分析表明,我国金融压力呈现出周期性特征,金融风险处于较高水平,但总体水平可控。陈忠阳等[9-11]考虑了金融子市场压力指数在时间维度上的相关性,认为在相关性较高时期,子市场风险溢出效应较大,系统性风险也较大。
由于仅测度金融压力指数无法直观反映金融风险的程度和状态,所以近年来学界强化了对金融压力状态识别问题的研究。秦建文等[12-14]利用马尔科夫区制转换模型、Logistic模型对金融压力状态进行识别,分析不同状态转换的概率。章曦[15]将金融压力指数的测度、识别和预测纳入同一分析框架,通过建立识别指数以有效识别系统性金融风险的程度。马勇[16]采用指数识别法和事件识别法来识别金融风险。许悦[17]采用门限自回归模型识别金融压力,研究金融风险状态与经济活动之间的格兰杰因果关系。Yao[18]认为在确定金融压力状态的阈值后,金融压力指数可有效识别压力状态。
综上可知,学界关于金融压力指数的测度、识别和应用等成果较为丰富。在测度方面,已有研究经历了从静态赋权法到动态赋权法的演变,使金融压力指数的测度更及时、准确;在识别方面,已有研究形成了较为有效的测度方法,能够区分金融风险的不同状态;在应用方面,已有研究主要集中在金融风险与宏观经济的非线性传导关系上。但已有研究也还存在一定不足。比如,采用的识别方法比较单一,主要为马尔科夫区制转换模型和Logistic模型等非线性自回归模型,对风险识别理论的研究较少,未能深刻剖析金融风险状态变化的原因;再如,学界对金融压力指数的识别重视不够,这可能导致在研究金融风险的非线性传导关系时,对于风险状态变量的设置存在一定偏误。本文从金融压力指数识别角度出发,构建指标体系测度金融压力指数,通过B-N数据分解法将金融压力指数分解为随机冲击、确定项和周期项,并根据分解结果进行识别,以期更好地把握金融风险识别的理论依据。
二、变量选取与研究方法
(一)金融市场的风险因素与指标选取
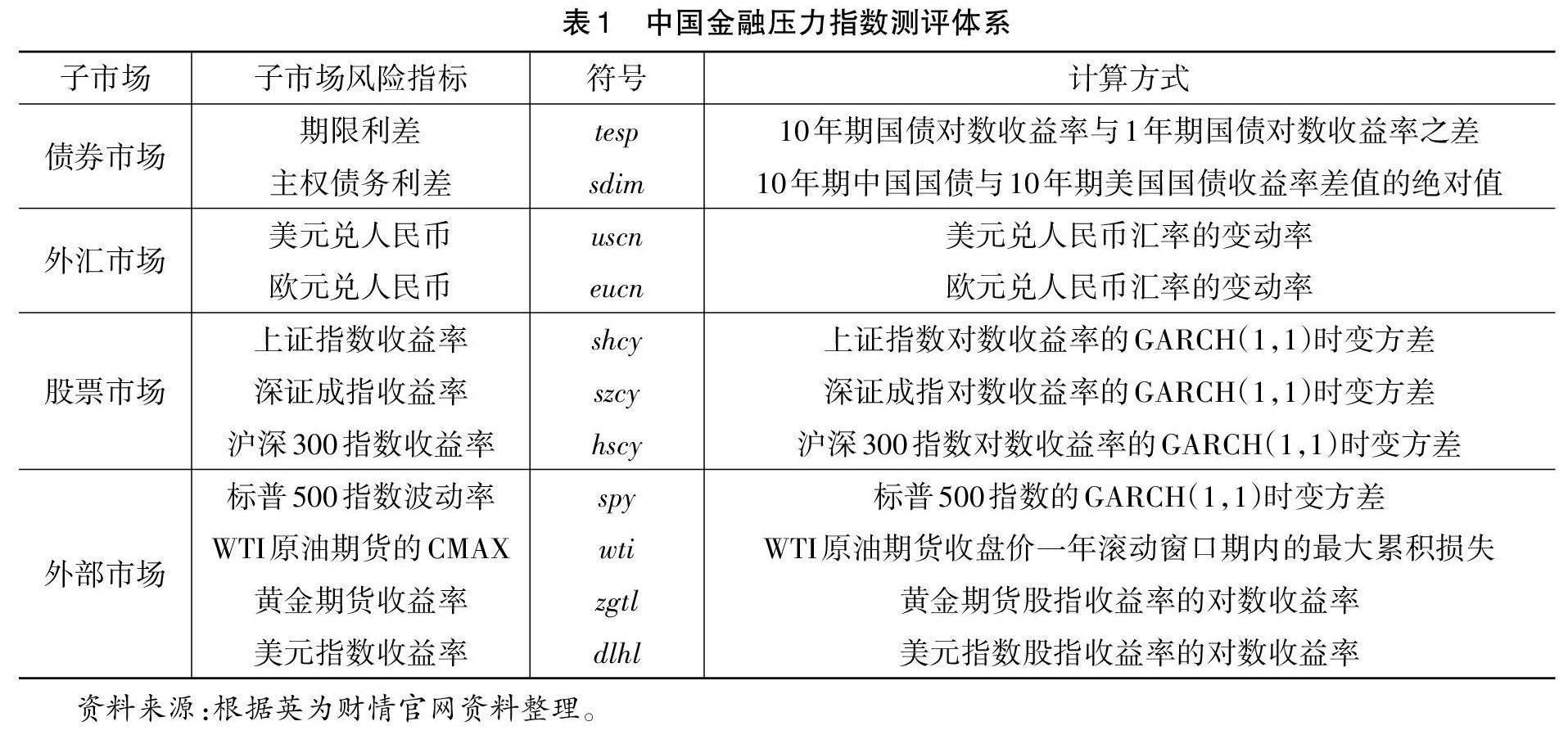
国内股票、债券、外汇等内部市场变动会直接影响投资者和金融机构决策,对中国金融市场稳定造成较大影响。同时,国际大宗商品期货价格变动、美国股票指数变动等外部市场风险也会影响国内投资者和风险管理部门决策,进而影响中国金融市场稳定。因此,本文将金融市场划分为债券市场、外汇市场、股票市场和外部市场,先测算各金融子市场的压力指数,再合成中国金融压力指数。本文借鉴已有文献[1,14],选择日度频次进行研究,以保证指标具有更强的时效性。本文构建的指标体系见表1,样本区间为2004年9月3日到2020年6月24日,共3632个样本。
债券市场的测度指标包括期限利差和主权债务利差。期限利差主要反映债券市场长期风险与短期风险的关系,该指标值越大,说明投机机会越多,债券市场风险越大。主权债务利差主要反映长期内人民币与美元的投资利差。当中国长期国债收益率高于美国长期国债收益率时,具有投机性质的“热钱”会大量流入我国,影响我国债券市场供需平衡,对债券市场带来一定波动;同时,我国央行为维持货币供应量和利率,会以人民币收购一部分外币,这会进一步影响我国货币供需稳定。因此,主权债务利差越大,国外“热钱”流入越多,越不利于我国金融市场稳定。
对外汇市场的测度以美元兑人民币汇率和欧元兑人民币汇率的变动率来衡量。外汇市场主要考虑因人民币升值或贬值所带来的资本异常流动风险。本文选择汇率变动率而非汇率波动率进行测度的原因是:第一,虽然外汇波动率可以描述汇率变动的速度和幅度,但却不能刻画人民币升值和贬值程度。相较于汇率波动率,汇率变动率可以有效反映人民币升值和贬值程度,而人民币升值和贬值都会对国内货币市场造成一定冲击。第二,由于我国实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度,因而汇率制度受政策的影响较大。汇率制度改革后,人民币汇率的波动率会在汇改后出现异常波动,此时出现的波动更多与政策干预有关,而并非市场行为所致。此外,央行一直将维持人民币汇率的基本稳定作为主要目标,这就决定了长期来看汇率波动率不会很大,不能真实反映外汇市场风险状态。因此,本文选择美元兑人民币汇率和欧元兑人民币汇率的变动率作为衡量外汇市场的风险指标更为合理。
股票市场的测度指标包括上证指数收益率、深证成指收益率和沪深300指数收益率。本文使用较为成熟的研究方法,采用时变方差刻画各指数风险。首先通过3种指数的日度收盘价求对数收益率,其次利用GARCH模型获得时变方差,最后进行合成,以此来衡量我国股票市场的风险水平。此外,根据有关学者的研究,在GARCH模型族中,GARCH(1,1)模型就已能够描述金融资产的风险状态,为计算方便,本文在数据预处理时统一采用了GARCH(1,1)模型。
外部市場主要衡量因外部政治经济环境突变所带来的风险。由于我国金融体系建立较晚,金融市场发展尚不成熟,加之受经济全球化等影响,当前我国金融市场受到的国外金融风险冲击越来越多。因此,本文在外部市场中引入了多项风险指标,主要包括美国标普500指数波动率、WTI原油期货收盘价一年移动窗口内的最大累积损失、黄金期货收益率和美元指数收益率。其中:标普500指数、黄金期货和美元指数的风险用时变方差度量;WTI原油期货采用日度收盘价计算一年滚动窗口期内每个交易日的最大累积损失,该指标可反映世界原油期货价格变动时的市场风险。
(二)金融风险的测度和识别方法
金融风险量化是研究金融风险性质时要解决的主要问题。金融风险并不仅仅是由金融体系中单一市场导致的,而是一种传导和扩散性风险,某一金融市场的突发性事件不仅会对自身产生影响,还会对其他金融市场产生影响。因此,在测度金融风险时不能只考虑某一金融市场的风险状况,还应考虑市场之间的传导和扩散效应。下文介绍研究中所使用的风险测度模型和方法。
1.金融压力指数的测算方法。金融压力指数的测算涉及两个环节,即数据预处理(包括风险指标的测度和数据标准化处理)以及金融市场风险合成(包括各子市场风险合成和金融市场风险合成)。
在数据预处理环节,波动性主要用GARCH模型残差的时变方差来表示。模型形式为:
[σ2t=α0+i=1pαiε2t-i+…+j=1qβjσ2t-j] (1)
其中,p为[ε2t]的滞后阶数,q为[σ2t]的自回归阶数。模型(1)为GARCH(p,q)模型,满足如下条件:[α0>0];[α1,…,αp≥0];[β1,…,βq≥0]。
通常,最常用的模型为GARCH(1,1)模型,其方差方程为:
[σ2t=α0+α1ε2t-1+β1σ2t-1] (2)
式(2)满足[α0>0],[α1≥0],[β1≥0]。虽然在GARCH模型的建模过程中有比较合理和实用的方法确定模型滞后阶数,如AIC信息准则、BIC信息准则等,但选择GARCH(1,1)模型就已能够解释金融资产收益率存在的异方差现象。Illing等[1,8]利用GARCH模型计算代表性金融资产的时变方差时,也采用了GARCH(1,1)模型。本文沿用这一思路,对子市场风险指标采用GARCH(1,1)模型来计算时变方差。
最大累积损失(CMAX)可以很好地测度资产风险,其为某一时刻金融资产的价格水平与前T个交易日期内价格最大值的比值(T取1年内的总交易日数)。该比值越小,表明金融风险越大。因此,最大累积损失与金融风险呈反向相关关系。Illing[1]将最大累积损失引入系统性金融风险指标中,用于测度加拿大系统性金融压力指数。国内相关学者为了方便对最大累积损失进行正向标准化处理,对最大累积损失进行了改进,使其与金融风险正相关。既有文献采用的滚动窗口期多有所不同,以一年365天计算,双休日和法定节假日暂停交易,则交易日约为250天左右,故本文采用向前250天作为滚动窗口期进行滚动计算。最大累积损失(CMAX)的计算公式为:
[CMAXt=1-xtmax[x∈(xt-j/j=0,1,2,…,T)]] (3)
式(3)中,[CMAXt]为t时刻金融资产最大累积损失,[xt]为t时刻资产价格,[max[x∈(xt-j/j=0,1,2,…,T)]]为过去T期滚动窗口期内金融资产价格的最大值。
为减少量纲的影响,本文对各金融子市场指标数据进行标准化处理。因子市场风险指标影响方向均已调整为正向,故本文采用正向极值法对数据进行标准化处理。标准化处理公式为:
[x*tj=xtj-minj(xtj)maxj(xtj)-minj(xtj)] (4)
式(4)中,[xtj]为原始数据,[x*tj]为经过正向标准化处理后的数据。
在金融压力指数测度环节,假设金融市场内第[i]个子市场的第j个风险指标权重为[ωij],[fsiit]表示第[i]个子市场在[t]时刻的金融压力指数,则子市场权重[ωij]的计算公式为:
[ωij=1Stdijj=1m1Stdij] (5)
式(5)中,[Stdij]为第[i]个子市场第[j]个指标的前250天滚动标准差。将权重[ωij]与风险指标数据标准化得分进行加权求和,可以构建第[i]个子市场的金融压力指数模型,模型形式为:
[fsiit=j=1mωij×x*tj] (6)
关于指标权重的计算,已有研究主要采用因子分析法、熵值法、静态CRITIC赋权法等方法。其中,静态CRITIC赋权法能够刻画子市场间的风险溢出效应,而因子分析法和熵值法在测算金融压力指数时并未考虑子市场间的风险溢出性,故静态CRITIC赋权法有一定的优越性。金融市场各子市场间的风险传导是时变的,在风险较小时,子市场间的风险溢出性并不明显,而一旦金融市场出现高风险冲击,则该冲击风险会由一个子市场迅速传至其他子市场。静态CRITIC赋权法所计算的风险相关系数[rik]是静态的,不能有效刻画子市场风险溢出的时变特征。在式(7)中,通过对相关系数[rik]进行改进,可使其能以T个时期为滚动窗口期滚动计算相关系数,如此便可将相关系数[rik]改进为动态相关系数[rik,t-T],改进的动态CRITIC赋权法能够更好地刻画风险溢出的时变特征。由于动态CRITIC赋权法允许子市场间的相关系数随时间变化,计算得到的金融压力指数更精确且更具时效性,因而本文采用动态CRITIC赋权法计算权重[ωi,t],计算公式为:
[ωi,t=ci,ti=1nci,t] (7)
式(7)中,[ci,t=σi,t-Ti=1n1-rik,t-T],[σi,t-T]为第[i]个子市场的金融压力指数在前T个滚动窗口期内的滚动标准差,[rik,t-T]为第[i]个子市场和第[k]个子市场在前T个滚动窗口期内的动态相关系数。
2.金融风险状态的识别方法。风险状态识别主要涉及马尔科夫区制转换模型和B-N数据分解法。
其一,马尔科夫区制转换模型。金融风险状态识别是测算金融压力指数的一个重要目的,可据其确定高风险和低风险时刻。模型识别法对于识别金融风险状态有很好的效果,它不仅可以识别金融风险的不同状态,还可估计状态转换的概率。常用的识别模型有马尔科夫区制转换模型、Logistic模型等非线性模型。本文以马尔科夫区制转换模型为例,分析中国金融风险状态特征,模型形式如下:
[FSIt=α(st)+β1(st)FSIt-1+…+βp(st)FSIt-p+μt] (8)
模型中:[FSIt]为[t]时刻金融压力指数,[α(st)]为常数項,[β1,β2,…,βp]为自回归模型中滞后项的系数向量,残差项[μt?IID0,st],[st]为时间[t]的不可观测的状态随机变量,由马尔科夫链过程生成。马尔科夫链过程定义为当前样本值只受前一期样本值的影响,即:
[pij=Pst+1=j|st=i] (9)
式(9)中:[pij]为生成[st]的概率,且满足[j=1Npij=1],[i∈1,2,…,N],[j∈1,2,…,N];N表示区制分类,通常设置风险状态为高、低两种区制,因而N取值为2。
本文采用一阶两区制马尔科夫链过程,令[i=0],[j=1],则区制转换概率P为:
[P=Pst+1=0|st=0Pst+1=1|st=0Pst+1=0|st=1Pst+1=1|st=1=p1-pq1-q] (10)
式(10)表示在t期为低风险状态的条件下,t+1期为低风险状态的条件概率为p, t+1期为高风险状态的概率为1-p,显然二者概率满足总和为1的条件。
其二,B-N数据分解法。B-N数据分解法常被用于分析宏观经济问题中由突发事件或外生事件所带来的冲击效应[17]。设[fsi]为金融压力指数,则[fsi]的一阶差分值可由下式表示:
[Δfsit=μ+εt+i=1∞γi×εt-i] (11)
式(11)中:[Δfsit=fsit-fsit-1],表示金融压力指数的一阶差分序列;[μ=t=2nΔfsitn-1],表示一阶差分序列在样本期内的均值;[εt]是服从均值为0、方差为[σ2]的随机变量。根据B-N数据分解法的分解原理,[fsii]的确定项趋势DTt可以分解为:
[DTt=fsi0+μ×t] (12)
式(12)中,[fsi0]是金融压力指数的初始值,[t]为样本数。随机游走趋势项[Tt]可以分解为:
[Tt=fsit+φΔfsit-μ1-φ] (13)
式(13)中,[φ]為[Δfsi]的一阶自回归系数。由此,周期项Ct可以分解为:
[Ct=-φΔfsit-μ1-φ] (14)
结合以上3个公式,随机冲击项STt可表示为:
[STt=fsit-Ct-DTt] [=fsit+φΔfsit-μ1-φ-fsi0+μ×t] (15)
三、金融压力指数的测算及分析
(一)子市场金融压力指数趋势分析
由表2可初步了解子市场金融压力指数的统计特征。债券市场金融压力指数主要刻画因债券利差所产生的风险。债券利差大,表明债券市场有大量投资机会,此时投机资本会流入债券市场,产生一定风险;债券利差小,说明短期内投资机会少,此时投机资本流动性较差。外汇市场金融压力指数主要刻画因人民币币值变化所引起的国际资本流动风险。人民币币值变化会引致国际“热钱”流动,冲击我国货币体系。股票市场金融压力指数主要刻画股价波动所带来的风险。在一定时期内,股票市场波动率小,说明市场较稳定,投融资活动产生的风险小;若股票市场波动率大,则会导致投资者产生恐慌情绪,抑制投资积极性。外部市场金融压力指数主要刻画大宗商品期货市场的风险。大宗商品期货价格变动与国际金融市场稳定之间密切相关。期货价格异常变动既会引起投资者恐慌,又会刺激投机行为,造成金融市场波动。由表2可以初步判断,各子市场金融压力指数具有显著差异。债券市场、外汇市场和外部市场的平均风险值较为接近,股票市场的平均风险值较小。从变化程度来看,债券市场和股票市场的变化大于外汇市场和外部市场。从区间来看,外汇市场和股票市场的区间比债券市场和外部市场大。从偏度来看,债券市场、股票市场和外部市场为右偏,外汇市场为左偏。
1.债券市场金融压力指数分析。从图1可以看出,2003—2020年间,我国债券市场共出现了5次较高风险时期。第一次是2004—2005年,为防止投资过热,国务院于2004年3月采取了紧缩性措施,央行配合实施了压缩信贷规模的货币政策,使得债券市场大幅波动。第二次是受2008年美国次贷危机影响,金融风险达到了样本期内的最大值。第三次是2014—2015年,债券市场进一步开放,企业资产债券化进程加快,但信用违约事件增加,风险随之增大。第四次是2018年,债券违约逐渐呈常态化趋势,同时受中美贸易摩擦等影响,部分企业经营成本上升,偿债能力下降,加剧了债券市场风险。第五次是2020年,受新冠疫情影响,企业经营状况不佳,偿债能力下降,债券违约风险上升。但随着复工复产的推进,企业生产能力得到释放,债券风险迅速降至低点。
2.外汇市场金融压力指数分析。由图2可知,外汇市场金融压力指数的变化主要与我国汇率制度市场化改革紧密相关。1994—2005年间,我国实行并轨制汇率制度,官方汇率与调剂汇率并行,其主要特点是盯住美元,人民币币值只受美元币值影响。因此,这一阶段外汇市场压力较小。2005年汇率制度改革之后,不再以单一美元为标准,而是实行参考一篮子货币进行调节的浮动汇率制。2006—2015年,即使发生了次贷危机,但汇率波动并不大。主要原因是此时我国还未完全放开汇率市场,央行为防范投机资本流入,利用外汇储备干预外汇市场、稳定汇率,缩小汇率浮动区间,降低了美元贬值对人民币币值的影响。自2015年8月11日起,汇率中间价决定权逐步开放,再次推动了汇率市场化进程。此次汇改之后,人民币汇率波动性明显上升,汇率市场化程度进一步加深。
3.股票市场金融压力指数分析。由图3可以看出,我国股票市场经历了3次较为严重的风险时期。第一次是在2007年,为抑制股市过热,财政部将证券交易印花税税率由1‰上调到3‰,此举对股票市场造成了很大波动。第二次是在2008年,为缓解美国次贷危机的冲击,我国进一步扩大内需、刺激投资,资金多流入基础设施领域和房地产行业,分担了部分次贷危机风险,但也抬高了经济杠杆率。第三次是在2015年,这是继2008年次贷危机后的又一次较为严重的风险时期。高杠杆率资本面对股市下跌表现出极高的敏感性,一旦出现不利信息,极易形成较大风险。
4.外部市场金融压力指数分析。由图4可以看出,外部市场的主要冲击来自国外重大事件。2008年次贷危机使得美国房地产泡沫破裂,房贷违约事件激增,股市剧烈动荡。2016年外部市场波动较大,不确定因素增加。从政治层面来讲,国际政治形势持续动荡,英国脱欧、美国大选等对全球经济形势有很大影响。从经济层面来讲,2016年世界经济低迷,需求不振,同时全球资产泡沫扩大、美联储加息、不良贷款率上升等,进一步加剧了金融形势困境。2020年初的外部市场压力主要来源于新冠疫情导致的美股暴跌,连续触发熔断机制,造成投资者恐慌。
(二)金融压力指数的分布特征
利用动态CRITIC法可对债券市场、外汇市场、股票市场、外部市场4个子市场的金融压力指数进行合成,从而得到整个金融市场的压力指数。分析主要从两个维度展开:首先,从时间维度分析样本期内我国发生的重大风险事件;其次,为弥补时间维度分析的不足,采用核密度估计方法对金融压力指数进行分析,以全面把握金融市场风险特征。
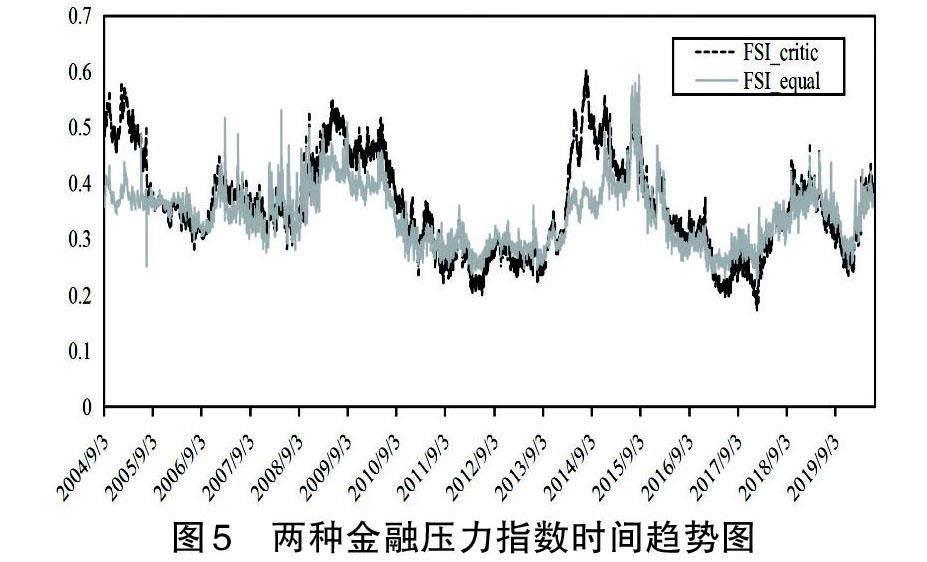
1.金融压力指数趋势分析。图5为以等方差法和动态CRITIC法测度的金融压力指数时间趋势图。通过对比可以发现:第一,两种指数对研究期内发生的重大金融风险事件都有一定程度的反映,基本展现了研究期内我国发生的主要风险事件,其中包括金融市场自身发生的风险事件,还体现了受国际环境等因素的影响而产生的风险。2008年美国次贷危机和2015年中国股灾主要是因金融市场缺乏有效监管造成的,2018年和2020年则更多是受国际贸易冲突和新冠疫情等金融体系之外的事件影响。这说明,只要某一事件会造成资产价格不合理波动,其就可能造成金融压力指数上升。第二,两种指数的波动性有所不同,以动态CRITIC法测度的金融压力指数在发生风险事件时指数增幅较大,而以等方差法测度的金融压力指数在发生风险事件时指数增幅相对较小。这主要是因动态CRITIC法在测度金融压力指数时考虑了金融子市场之间的风险溢出和传导效应,子市场之间相关性越强,风险传导效应越大。金融风险较大时,投资者会在各种金融资产中进行选择,风险也会随之传导至其他市场。
2.金融压力指数的核密度分析。核密度曲线图能够描绘峰度、偏度、极大值、极小值和尾部特征等,可以借此从宏观上把握金融体系的风险状态。由图6可知:根据等方差法和动态CRITIC法测算金融压力指数进而绘制的核密度曲线图都呈现“尖峰厚尾”的特征,FSI_equal的最小峰度在6.5左右,超过了正态分布的峰度,FSI_critic的峰度在4.5左右。这说明等方差法和動态CRITIC法这两种方法都能在一定程度上刻画金融风险特征,但二者的区别更明显。一是以等方差法测算的金融压力指数有两个明显的峰值,分别位于0.3和0.38处;而以动态CRITIC法测算的金融压力指数只有一个明显的峰值,位于0.35处。由图5可知,FSI_equal在2004年9月到2008年9月以及在2010年9月到2014年9月间基本保持稳定,FSI_equal的核密度曲线在这两个区间附近形成了比较明显的聚集,数据密度较大。二是FSI_critic的样本区间比FSI_equal的样本区间更大,前者在0.1~0.6之间,而后者在0.2~0.6之间。FSI_critic的核密度峰值小于FSI_equal的核密度峰值。这主要是因动态CRITIC法能够捕捉到更为敏感的极端信息,而等方差法是一种静态赋权方法,不能有效捕捉极端值。三是动态CRITIC法比等方差法更能体现金融风险的“厚尾性”。由图6可以看出,FSI_critic的核密度曲线左右尾部均比FSI_equal厚,且右尾部又出现了一个小高峰,说明此处的风险值也出现了一定聚集,出现较高风险的次数较多。
由于动态CRITIC法具有更准确、动态的特性,故下文选择基于动态CRITIC赋权法计算的金融压力指数作为金融市场的风险指标,并对该指数作进一步分析。
四、金融压力指数分解与金融风险识别
(一)金融压力指数分解
为避免实证中出现伪回归现象,本研究对金融压力指数进行了平稳性检验,结果(限于篇幅,文中未列示)表明,以动态CRITIC法测度的金融压力指数的P值为0.0670,在5%的置信水平上不平稳,而其一阶差分序列的P值为0.0000,在5%的置信水平上平稳,故本研究采用差分后的数据进行金融压力指数分解分析。
由图7可知:第一,随机游走成分的走势和金融压力指数的走势相似度非常高,说明金融压力指数与随机游走成分具有很强的相关性。如2008年9月,美国次贷危机导致我国金融市场大幅波动,此时随机游走成分也出现大幅上升,表明这一时期金融市场不确定性增大,随机成分成为与金融风险相关性最强的因素。再如,2015年我国发生股灾,各大指数纷纷下跌,金融风险上升,此时随机游走成分同样呈现上升态势。在金融风险较为稳定的2011—2014年间,随机游走成分维持在0.3左右,未发生明显上升。这说明当金融市场面临较大冲击时,市场不确定性会增大,此时随机游走成分将会影响整个金融市场的风险状况。第二,金融压力指数的周期成分在金融风险较高时非常明显。金融风险较高时,周期成分非常明显,而金融风险越稳定,周期成分则越接近于0。在金融市场比较稳定的2012年和2017年,周期成分在-0.01~0.01之间变动;2008年9月和2015年9月前后,周期成分的变动范围扩大为-0.03~0.03。第三,结合随机游走成分和周期成分来看,金融压力指数的变化往往是受二者的综合影响。当金融市场较为稳定时,周期成分接近于0,此时金融压力指数主要受随机游走成分影响;当金融市场受到较大冲击时,周期成分会产生强烈波动,这种波动会作用于金融市场,导致金融压力指数上升。
根据B-N数据分解法,随机游走成分还可分解为随机冲击项和确定项。确定项趋势的经济含义是金融压力指数在长期内的量化趋势,主要根据金融压力指数的初始值、差分值和时间长度计算得到,其受金融压力指数初始值的影响较大。通过计算可知,确定项平均值为0.4481,最小值、最大值分别为0.3903和0.5060,方差仅为0.0011,说明在样本期内,我国金融市场面临的长期风险约为0.4481。确定项可被看作我国金融体系面临的一种长期风险,是由正常的经济活动所产生的风险。
发生金融危机时,金融风险除来自确定项的风险之外,还来自突发事件所带来的随机冲击,这种冲击是不可预期的,且随着金融活动范围的不断扩大,冲击来源越来越广泛。由图8可知:其一,随机冲击、随机游走、金融压力指数这3个序列的走势相似度较高,原因可能在于随机冲击项是随机游走成分的重要組成部分,而金融压力指数的走势极易受随机游走成分的影响。其二,随机冲击项为正的时期表示此阶段某种冲击会加剧市场上的金融风险,随机冲击项为负的时期则表示此阶段金融市场比较稳定,金融风险维持在可接受、可控制的范围之内。如2008年9月前后,随机冲击项为正,随机游走成分呈现上升态势,金融压力指数上升;2012年和2017年,随机冲击项为负,表明金融市场未发生明显的冲击性事件,随机冲击并未造成随机游走成分呈现上升态势,也未造成金融压力指数上升。其三,随机冲击上升阶段,金融体系可能面临一些潜在风险的冲击,当这种冲击小于0时,其对整个市场的影响可能并不明显,而一旦这种冲击大于0,则很可能演变为较为严重的金融风险事件,甚至可能演变为金融危机。相反,在随机冲击下降阶段,财政部、央行等部门可能为缓解金融风险过高的局面而通过财政政策、货币政策进行干预,政策措施的实施会遏制金融风险攀升的势头,逐步化解随机冲击所带来的风险,使得金融风险稳定在合理水平。因此,随机冲击的下降阶段往往伴随着有针对性的政策手段。
(二)金融风险识别
学者们在研究金融风险与宏观经济、政策效果等问题时,往往会考虑其中存在的非线性特征[11,17],在分析金融风险时也应根据金融风险的阶段性特征识别高低风险时期。目前学界主要采用马尔科夫区制转换模型来识别金融压力的高低状态。本研究先建立马尔科夫区制转换模型,检验金融压力指数是否具有明显不同的状态,并根据转换概率图分析样本期内状态变化的原因,再根据B-N数据分解得到的确定项对金融风险进行识别,最后对两种识别方法进行比较,总结各自的优缺点。
1.基于马尔科夫区制转换模型的识别。利用马尔科夫区制转换模型估计风险转换特征,结果(限于篇幅,文中未列示)表明:金融风险维持在低风险时期的概率参数估计值为0.9644,P值为0.0000,说明我国金融体系处于低风险状态,不易向高风险区制转换,具有一定黏性。由高风险向低风险转换的概率参数估计值为0.0986,P值为0.0000,说明存在由高风险向低风险转换的可能性,但持续时间较短,整个样本期内,我国金融风险整体处于可控范围之内。一般来讲,风险状态转换概率越高,金融市场越不稳定,若金融市场长期处于高风险与低风险的不断转换中,说明这一时期金融市场不断受到来自自身或外界不稳定因素的冲击,货币当局未能及时采取有效措施降低冲击带来的影响。我国金融风险区制转换概率较低,说明我国金融风险监管和降低风险的政策措施均有较好成效,但金融体系仍有一定概率处于高风险时期,这就要求在识别系统性金融风险的基础上,实施相应的政策措施以有效化解高风险,使高风险状态逐渐向低风险状态转换。
进一步地,本研究根据转换概率绘制了转换概率图,这样不仅可以了解每一时刻的风险状态,还可以清楚高风险和低风险的转换时期。由图9可以看出,金融压力处于高风险状态的时期分别为2008年9月至2009年2月、2015年2月至2016年1月。在2007年5月至2008年9月、2010年11月至2012年2月、2014年11月至2015年11月、2019年1月至2019年9月这4个时间段,金融风险状态转换较为频繁。在区制转换概率矩阵中,由低风险状态向高风险状态转换的概率为0.0356,而从高风险状态向低风险状态转换的概率为0.0986,说明我国金融体系整体风险由高风险向低风险状态转换的概率相对较大。
2.基于B-N数据分解法得到的确定项的识别。根据随机游走成分的确定项来识别金融风险高低状态的主要依据是:当金融市场未受冲击时,金融风险比较稳定,金融压力指数并未表现出较大波动,此时风险主要是正常经济活动产生的风险,即为随机游走成分中的确定项;当金融市场受重大事件冲击时,随机冲击的波动幅度增大,这时随机游走成分中随机冲击的影响增强,使得随机游走成分呈上升趋势,继而使得金融风险增大。因此,一旦金融压力指数超过随机游走成分中的确定项,则随机冲击产生的影响就会加剧金融风险。本文根据这一思路利用确定项来识别金融风险的高低状态。图10是根据确定项识别的状态图,DT线是确定项的均值。DT线之下为低风险状态,表示金融市场风险较小,随机冲击成分影响较小;DT线之上为高风险状态,表示随机冲击所占的比重逐渐增大,推动金融压力指数上升。由图10可知,样本期内,金融风险较高的时期主要有3个:2004年9月至2005年7月、2008年10月至2009年9月、2014年7月至2015年9月。可见,基于确定项的识别方法也能够有效识别中国金融市场的高风险时期,如2008年金融危机和2015年股灾等。这意味着基于确定项的识别结果与基于马尔科夫区制转换模型所得到的结论具有一定的相似性,基于确定项识别金融风险状态具有一定的合理性。
(三)两种识别方法的比较
第一,通过模型拟合,区制转换模型可以非常清楚地得到单个样本属于不同风险状态的概率,这对预测金融风险状态有重要意义,即可以通过金融压力指数来预测处于高风险和低风险状态的概率。区制转换模型能够识别出金融风险在不同状态之间转换的时期。例如,2007年9月至2008年9月,这期间金融风险状态发生了多次转换,说明这一时期金融市场出现了不稳定因素;从2008年美国次贷危机爆发到2012年9月,风险状态出现了较长时期的频繁转换,表明金融危机在较长时期内造成了我国金融市场不稳定。第二,区制转换模型具有较大灵活性,可以通过设置不同的区制个数计算多种状态的概率,因而对金融风险的识别更准确、高效。但是,区制转换模型只是通过金融压力指数来计算概率,并不能对金融风险进行更详细的分解,而利用B-N数据分解法得到的确定项来识别金融风险能够弥补这一不足。B-N数据分解法先分解得到影响金融风险的随机游走成分和周期项成分,又将随机游走成分分解为随机冲击和确定项,最后利用确定项来识别风险状态,这为金融风险的识别提供了理论依据,能够使区制转换模型得到的转换概率具有更强的理论意义。因此,基于马尔科夫区制转换模型和基于B-N数据分解法得到确定项这两种方法可从不同角度识别金融风险,是对风险识别的重要补充。
五、结论与建议
(一)主要结论
本文将我国金融市场划分为债券市场、股票市场、外汇市场和外部市场4个子市场,构建金融压力指数综合评价体系,利用标准差倒数权重法测算4个子市场的日度金融压力指数,采用等方差法和动态CRITIC法对各子市场的金融压力指数进行合成,分别得到静态和动态的金融压力指数,并利用核密度分析法绘制了核密度曲线。本文得到的主要研究结论为:其一,采用等方差法和动态CRITIC法得到的金融压力指数在描述金融市场风险时分布曲线的形状有明显差别,前者呈“双峰”特征,后者呈“单峰”特征,后者能够更好地描述金融市场出现的极端值,更准确地描述金融风险。其二,随机冲击是影响我国金融压力指数的重要因素,当某个金融事件所产生的随机冲击超过了随机游走成分中的确定项时,该冲击就会造成金融压力指数上升,意味着金融风险增大。在金融风险识别中,可以确定项为标准划分金融压力指数的风险状态。其三,以随机游走成分中的确定项和以马尔科夫区制转换模型对金融风险进行的识别表明,两种方法识别的风险状态较为接近,各有优劣。概率转换图对于单个样本的转换概率具有较好的估计效果,可以利用模型估计得到每一个样本的概率,对于金融预警及相关研究有很大帮助;而基于确定项的识别方法具有较强的理论意义,金融压力指数通过分解可得到随机游走成分和周期项,随机游走成分又可分解为随机冲击和确定项,当一个突发事件发生时,它通常是以随机冲击的形式影响金融市场,市场上的金融风险就会超过确定项的临界值,从而由低风险向高风险状态转换的概率会增大。因此,研究中这两种识别方法可以互为补充。
(二)政策建议
第一,建立更加完善的风险测度指标体系。随着世界经济的深度交融,一国的金融风险已不仅仅由自身的风险状况所决定,在量化风险时不仅要考虑国内金融风险因素,还要考虑外部风险事件的影响。事实证明,在我国防范和化解系统性风险的一系列举措下,整个金融体系的风险已经得到了很好的控制。但是,当前国际政治经济形势不容乐观,风险事件频发,不利信息会迅速扩散到金融市场,打击投资者信心,造成金融市场波动。此外,因一些西方国家实施制裁手段,我国外向型企业经营成本上升,盈利能力和偿债能力下降,企业违约有所增加,银行积累了较多不良贷款,影响了企业与银行之间正常的借贷关系,风险进一步由实体经济传至金融体系,对金融体系造成了一定冲击。因此,为有效度量金融市场风险,应建立一套更加符合我国实际的风险度量指标体系,不仅应包含国内风险指标,还应包括考虑外部风险的指标,风险监管机构和有关部门应主动对可能影响金融风险状态的突发性事件进行预估,预先制定合理可行的应急方案。
第二,制定相关政策时应考虑金融子市场间的风险溢出效应,提升政策有效性。当面临突发性风险事件时,有关部门往往会借助财政政策和货币政策来降低不利影响。相对于实体经济,金融体系的风险传导更为迅速和广泛。对于调控金融风险的货币政策,应考虑时效性,央行为抑制投资过热往往会采取紧缩性政策,这一行为会释放不利于投资的敏感信息,对金融市场产生迅速且严重的影响。因此,有关部门在制定相关政策时应保持谨慎态度,深入分析政策可能带来的后果,最大限度降低对市场的负面影响,提升政策有效性。同时,金融市场内部是相互影响的,风险也有很强的传导性,因而政策制定者在制定财政政策和货币政策时,应充分考虑金融子市场间的风险溢出效应。对单个市场的政策措施可能造成其他子市场波动,这种风险溢出效应可能增大整个金融体系的风险。因此,在制定政策时应全面考虑,综合利弊。当某项政策对其他子市场会产生不利影响时,可利用配套手段降低这种不利影响。另外,由于溢出效应具有时变特征,因而还应考虑对其他子市场的风险溢出程度。
第三,进一步完善监管制度,加强对风险的管理和防范。由于金融风险发生后相关部门所采取的调控措施容易引致其他风险,故对于金融风险的监管应以防范、预防为主。我国早期为促进实体经济发展,对金融创新多持宽松态度,供给和需求不断增加能够化解金融创新产生的一部分风险,但是近年来,随着供给过剩,供需矛盾逐渐加剧,企业经营成本上升,金融创新风险逐渐暴露出来。金融体系违约比例上升、不良贷款率上升等,都说明我国与金融创新相配套的监管制度和规范未充分发挥作用,金融监管仍需加强和完善。同时,之前因过于依赖金融创新,使得金融业未能给实体经济提供足够有效的资源配置,反而将筹集的资金用于具有更高風险的金融创新活动,在不断的金融创新中,风险必然逐渐积累。因此,今后在促进金融创新的同时,还应立足服务实体经济的本质要求,促进实体经济发展。随着金融创新的不断深化,可通过规范金融创新方式,使金融创新处于有效的监管之中。
参考文献:
[1]ILLING M,LIU Y.Measuring financial stress in a developed country:an application to Canada[J].Journal of financial stability,2006(3):243-265.
[2]HAKKIO C,KEETON W R.Financial stress:what is it,how can it be measured,and why does it matter?[J].Eco- nomic review,2009(2):5-50.
[3]BALAKRISHNAN R, DANNINGER S, ELEKDAG S,et al.The transmission of financial stress from advanced to emerging economies[J].Emering markets finance and trade,2011(sup2):40-68.
[4]OZCELEBI O.Assessing the impacts of financial stress index of developed countries on the exchange market pressure index of emerging countries[J].International review of economics and finance,2020(9):288-302.
[5]CEVIK E,DIBOOGLU S,KENC T.Financial stress and economic activity in some emerging Asian economies[J].Re- search in international business and finance,2016(C):127-139.
[6]王维国,王际皓.货币、银行与资产市场风险状况的识别:基于金融压力指数与MSIH-VAR模型的实证研究 [J].国际金融研究,2016(8):71-81.
[7]MACDONALD R,SOGIAKAS V,TSOPANAKIS A.Volatility co-movements and spillover effects within the Euro- zone economies:a multivariate GARCH approach using the financial stress index[J].Journal of international financial markets,institutions and money,2018(1):17-36.
[8]丁岚,李鹏涛,刘立新.中国金融压力指数的构建与应用[J].统计与信息论坛,2019(10):63-72.
[9]陈忠阳,许悦.我国金融压力指数的构建与应用研究[J].当代经济科学,2016(1):27-35+125.
[10]丁述军,庄须娟,李文君.区域金融风险部门间传染机理与实证分析[J].经济经纬,2019(3):1-8.
[11]姚晓阳,孙晓蕾,李建平.考虑市场相关性的中国金融压力指数构建方法与实证[J].管理评论,2019(4):34-41.
[12]秦建文,王涛.中国金融压力与宏观经济动态效应研究:基于MS-VAR模型的实证分析[J].中央财经大学学 报,2017(9):32-42.
[13]郑金麟,张业圳,谢八妹.我国系统性金融风险的衡量与识别[J].金融监管研究,2019(12):54-65.
[14]张勇,彭礼杰,莫嘉浩.中国金融压力的度量及其宏观经济的非线性效应[J].统计研究,2017(1):67-79.
[15]章曦.中国系统性金融风险测度、识别和预测[J].中央财经大学学报,2016(2):45-52.
[16]马勇,黄科.金融压力指数及其政策应用:基于中国的实证分析[J].金融监管研究,2019(7):1-17.
[17]许悦.系统性压力综合指数的有效性研究[J].统计与决策,2017(2):166-170.
[18]YAO X Y,LE W,SUN X L,et al.Financial stress dynamics in China:an interconnectedness perspective[J].Inter- national review of economics and finance,2020(7):217-238.
[19]JAMES C,MORLEY.A state-space approach to calculating the Beveridge-Nelson decomposition[J].Economics Le- tters,2002(1):123-127.
[20]李子聯,陈强.中国对外贸易的疫情冲击效应[J].现代经济探讨,2021(4):75-82.
[21]AKLAN N A, ?INAR M, AKAY H K. Financial stress and economic activity relationship in Turkey: post-2002 period [J].Journal of management & economics,2015(2):567-580.
[22]KIM H,SHI W,KIM H H.Forecasting financial stress indices in Korea:a factor model approach[J].Empirical eco- nomics,2015(1):1-40.
[23]BEVERIDGE S,NELSON C R.A new approach to decomposition of economic time series into permanent and transi- tory components with particular attention to measurement of the ‘business cycle[J].Journal of monetary economics, 1981(2):151-174.
[24]KIM C J.Markov-switching and the Beveridge-Nelson decomposition:has US output persistence changed since 1984?[J].Journal of econometrics,2008(2):227-240.
[25]清華大学国家金融研究院金融与发展研究中心课题组.中国系统性金融压力的监测[J].国际金融研究,2019 (12):3-12.
[26]李子联.进出口贸易中不确定性事件的冲击效应[J].财经理论与实践,2010(6):77-82.
(责任编辑:甘海燕)

