直升机声学超材料舱壁的低频多带隙降噪特性

王晓乐，孙萍，顾鑫，赵春宇，黄震宇

1.上海交通大学 感知科学与工程学院，上海 200240

2.航空工业空气动力研究院 气动噪声重点实验室，哈尔滨 150001

直升机作为一种多功能的空中平台在军事突袭任务、灾难空降救援、紧急医疗运输以及现场新闻报道等多种用途中发挥着举足轻重的作用［1-2］。然而，直升机的动力配置方式会产生高量级的舱内噪声，从而使得直升机的驾乘舒适度远不及固定翼飞机。直升机高强度的舱内噪声不仅容易引起驾乘人员烦躁疲劳、注意力下降，而且可能损伤人员听力；此外，语音通话信号和仪表报警信号还极易受到舱内噪声的掩盖而影响正常飞行操控，甚至可能导致严重事故［3］。

引起直升机舱内噪声的主要振/声激励源包括：发动机-齿轮箱-传动轴系统、主旋翼、尾旋翼以及湍流边界层［4］。这些激励源主要通过2 类传递路径对舱室声学环境产生影响：一是结构声传递，即发动机-齿轮箱-传动轴系统的机械振动，通过支撑杆等连接结构传递至舱室壁板，进而向舱内辐射噪声；二是空气声传递，主旋翼、尾旋翼以及湍流边界层所产生的空气声波，通过壁板、舱门、风挡、孔隙等结构透射至舱室［5-6］。基于此，直升机舱内噪声频谱呈现独特的离散音调宽带分布特征［6-7］。尽管不同直升机型号对应的舱内噪声频谱会存在一定的差异，但500 Hz 以下频段的噪声量级通常会超过100 dB，是亟需降低的主导频段。

直升机舱内噪声的控制可以从振声激励源抑制、传递路径控制和接收者保护3 个方面入手。对于振声激励源的抑制，诸如旋翼叶片数量、面积、扭曲和形状修改，旋翼叶片通过速度控制，发动机-齿轮箱-传动轴改型等方式，设计和实施难度大，容易影响转子稳定性、机身操控性、空气动力学效率、载荷承重和航程能力，因而牵扯一系列的适配、权衡与验证过程，需要在直升机总体设计阶段便实施，难以用于已定型机型［7-10］；对于接收者的保护，尽管直升机驾乘人员在整个飞行任务中都需要佩戴耳罩，但是最近公开文献对支奴干CH-147F 型直升机进行的舱内噪声暴露测试表明：现有耳罩很难提供足够的500 Hz 以下频段的噪声防护［11］；相较而言，从传递路径进行控制，实现振动与噪声的隔离与吸收，是直升机舱内降噪最为行之有效的方法，其设计和实施难度都较小，尤其适用于已定型机型的改造。

当前的传递路径控制技术可分为无源控制和有源控制两种。其中，无源控制技术主要包括在关键传递路径结构处加筋或附加质量、安装动力吸振器、敷设阻尼和多孔吸声材料等方法，其优点是性能可靠、鲁棒性高且造价低廉，但是受到重量代价和安装空间的严格限制，已被证明很难满足直升机500 Hz 以下低频的舱内降噪要求［12-14］。有源控制技术主要利用扬声器产生次级声场干涉或利用机电/压电作动器抑制结构声辐射的原理达到舱内降噪目的，其低频控制效果比无源控制技术好，但是受到作动器和误差传感器布点数量、放置位置以及系统复杂度的限制，存在全局控制性能不佳、鲁棒性差且成本造价高等缺点［15-17］。因此，迫切需要发展适用于直升机舱内降噪应用的传递路径控制新技术，以期形成一套对附加重量、改造成本、飞行性能影响小且满足驾乘舒适度要求的噪声控制策略。

由于直升机舱壁是结构声和空气声传递路径的共经结构，对其进行声学性能的改造成为直升机舱内噪声控制难题破局的关键。近年来提出的基于局域共振原理的声学超材料突破了常规声学材料工作机理上的桎梏，以其小尺寸结构控制大波长声波的工作特征，为解决低频振动与噪声控制问题提供了全新思路［18-22］。声学超材料包含可人为设计的微观结构（亦称“单元”），通过精准设计单元的局域谐振与耗能模式，使得声学超材料在宏观层面呈现自然材料所不具备的超常动态特性，进而赋予声学超材料卓越的振声调控特性。通过在杆、梁、板、壳等传统工程结构上周期性地附加局域共振单元，可以构建一类局域共振型声学超材料结构，这类新型结构可以形成低频弹性波带隙，在带隙频率范围内可以显著地抑制弹性波的传播与辐射［23］。目前涉及的声学超材料结构大多一个单元中仅含有一个局域共振系统，而且考虑的基本都是单自由度或单方向谐振［24-32］，这样的结构形式显然无法满足直升机500 Hz 以下的宽带舱内降噪应用需求。尽管可以将结构形式更为复杂的局域共振单元引入声学超材料结构的设计，从而实现更为丰富的低频带隙行为［33-40］，然而复杂的结构形式却容易造成声学超材料结构的制备与施工工艺复杂化，反过来造成声学超材料结构的应用障碍。

本文将声学超材料结构的思想引入直升机舱壁声学性能的改造，构造一类针对直升机500 Hz以下低频舱内降噪要求的多带隙声学超材料结构。建立这类声学超材料结构的有限元动力学模型。开展小尺寸均匀平直板安装所提出声学超材料样件的隔声性能和振声性能试验，验证有限元动力学模型的有效性。最后，将声学超材料样件应用于大尺寸壁板结构，并分别开展隔声性能和振声性能试验，用以评估实际效果。所提出的多带隙声学超材料结构形式简单、批量制备方便、低频性能优异，有望成为解决直升机舱内降噪难题的潜在方案。

1 声学超材料结构设计

构造声学超材料局域共振单元的结构形式多种多样，为了充分考虑直升机舱壁的实际工作环境以及声学超材料的制备方便程度，选择带有端部质量的悬臂梁作为共振结构，经由支撑将共振结构连接至振动基板，承受结构振动和空气声波的复杂激励。图1 所示为提出的声学超材料结构及其构成单元的结构示意。其中，每个单元内部包含4 个共振结构，通过调整端部的质量和悬臂梁的刚度，可以灵活设计各个共振结构的谐振频率，按照谐振频率由低到高，依次将单元中的4个共振结构标号为1～4。

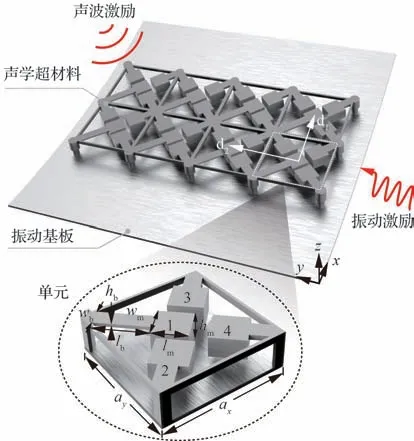
图1 声学超材料结构的基本形式Fig.1 Basic configuration for acoustic metamaterial structure

对于单个共振结构，其关键几何参数为：端部质量的长度lm、宽度wm和厚度hm，悬臂梁的长度lb、宽度wb和厚度hb。由于声学超材料的优异声学特性来源于其自身的结构形式而非材料组分。因此，对于声学超材料的构成材料并无特殊要求，可选用质量密度小，加工性能佳，阻燃无毒的航空适用材料。

需要说明的是，为了使所提出的声学超材料结构具有显著的带隙特性，必须满足2 个设计条件：①每个单元的特征尺寸（ax或ay，亦称晶格常数）须小于振动基板中所关注弹性波波长的一半［41］；②每个单元中由单个共振结构所贡献至振动基板上的力净和应非零［42］。

2 声学超材料结构动力学模型

忽略结构阻尼，在长波极限条件下，图1 所示的声学超材料结构可以模化为图2 所示的动力学模型。该模型包括2 部分：一部分为分布参数的振动基板，另一部分为周期性分布于振动基板上的集总参数“质量-弹簧”共振结构。

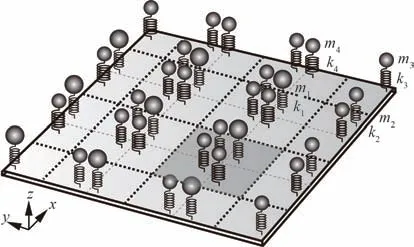
图2 声学超材料结构动力学模型示意图Fig.2 Dynamic model schematic for acoustic metamaterial structure

由于实际情况下的直升机舱壁面板的法向维度远小于其面内维度，故可采用Kirchhoff 薄板理论描述振动基板的弯曲振动特性。在所采用的有限元法中，将振动基板离散为4 节点的矩形单元网格，每个节点计及3 个位移自由度：挠度w，绕x轴的转角θx，绕y轴的转角θy。为简化分析，假设附加的“质量-弹簧”共振结构仅影响振动基板单元节点处的横向位移，而对绕x轴和y轴的转角不产生作用。

对于无限大尺寸的声学超材料结构，每个单元中均存在4 个“质量-弹簧”共振结构，其质量大小和弹簧刚度分别用m1～m4和k1～k4表示。为了建模方便，如图2 中粗虚线所示，将声学超材料结构的单元进行重新划分，从而使得4 个“质量-弹簧”共振结构的作用点得以合并。假设振动基板上安装有N个声学超材料单元，共计4N个“质量-弹簧”共振结构，记第p个“质量-弹簧”共振结构安装在振动基板的第q个节点处。根据牛顿第二定律，第p个“质量-弹簧”共振结构的质量矩阵mp和刚度矩阵kp可表述为

进一步建立振动基板与共振结构的耦合振动方程，耦合后整体系统的质量矩阵M和刚度矩阵K可表述为［43］

式中：F和q分别为整体结构的广义力矢量和横向位移矢量；ω为圆频率。

3 带隙特性计算与分析

声学超材料最重要的特性之一便是所谓的带隙特性。在带隙频率范围内，波无法在结构中自由传播。本节首先给出详细的带隙特性计算方法，进而开展算例研究，分析所提出的声学超材料结构的带隙特性及形成机理。

3.1 带隙特性计算方法

基于有限元法，声学超材料结构单个单元的动力学控制方程可表述为

式中：KC和MC分别为单元的刚度矩阵和质量矩阵；qC和FC分别为单元节点的广义位移矢量和广义力矢量，具体元素为

式中：上标T 代表转置。如图3 所示，各元素下标L、R、B、T、I 分别表示单元左边界、右边界、下边界、上边界及内部，各元素下标LB、LT、RB、RT则表示单元左下、左上、右下、右上4 个角节点。

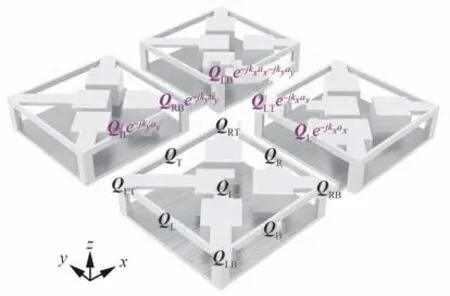
图3 4 个相邻单元的位移及受力关系Fig.3 Displacements and forces at the boundaries of four connected unit cells

通过考虑单元边界条件的周期性，可以简化单元动力学控制方程式（6）。根据Bloch 定理［44］，当波从参考单元沿着2 个基矢方向分别移动n1d1和n2d2至目标单元时，目标单元节点处的广义位移矢量和广义力矢量（以Qtar指代）可由参考单元节点处的广义位移矢量和广义力矢量（以Qref指代）经相因 子eμ1和eμ2缩放获得。其中，d=[d1，d2]表示单元基矢，μ=[μ1，μ2]表示传播矢量，两者存在式（9）所示的关系。

式中：k=[kx，ky]为Bloch 波矢。于是，二维周期系统的Bloch 定理可以表述为

式中：rtar=rref+n1d1+n2d2；rtar和rref分别为目标单元和参考单元的径矢；n1和n2分别为沿着单元的2 个基矢分量d1和d2移动的倍数，可写为矢量形式n=[n1，n2]T。据此，图3 给出了4 个相邻单元边界处的位移相容和力平衡关系示意。

根据式（10），单元各边界处的广义位移矢量存在以下关系［45］：

将式（11）～式（15）表示为矩阵形式：

式中：

=[qB，qLB，qL，qI]T。R(kx，ky)中I矩阵为单位矩阵，其下标表示该单位矩阵的维数对应于相应边界和角点上的自由度数。

同样，根据式（10），单元边界处的受力关系可表示为［45］

4 个单元公共角点处的受力关系为

将式（16）代入式（6），可得：

在式（20）两边同时乘以R(kx，ky)的共轭转置矩阵RH(kx，ky)，可得约简形式的单元动力学控制方程：

将式（17）～式（19）代入式（20）的右边并展开得：

由于考虑的是自由波传播问题，因此FI=0，进而可将式（21）转换为本征值问题：

式中：(kx，ky)=RH(kx，ky)KCR(kx，ky)，(kx，ky)=RH(kx，ky)MCR(kx，ky)分别为单元约简形式的刚度矩阵和质量矩阵。每给定一组Bloch 波矢k可得到一组本征值和本征向量。为了减少计算量，充分利用单元的对称性，可将Bloch 波矢k仅设定在不可约 Brillouin 区的边界（Γ→X→M→Γ，见图4）。计算得到的本征频率ω即对应在声学超材料结构中可自由传播的本征波的频率。而本征频率ω随Bloch 波矢k的变化曲线即为能带结构图，其中不存在任何色散曲线的频率范围即为带隙。

图4 无限尺寸原始板（虚线）与声学超材料板（圆点）的能带结构比较Fig.4 Comparison of band structures of infinite pristine plate（dotted lines）and acoustic metamaterial plate（filled circles）

3.2 带隙特性算例分析

基于所建立的声学超材料结构单元无阻尼自由弯曲振动的有限元模型，本节开展算例研究，计算分析无限大振动基板附加声学超材料后的带隙特性。

首先，需确定单元的特征尺寸。振动基板中传播的弯曲波的波长λp为

式 中：hp和Dp=分别为振动基板的厚度和弯曲刚度；ρp、Ep和νp分别为振动基板材料的密度、杨氏模量和泊松比。为了有效体现声学超材料的局域共振带隙特性，单元的特征尺寸须满足［41］

对于铝制振动基板，其具体材料参数取ρp=2 700 kg/m3，Ep=69 GPa，νp=0.33。鉴于主要关注500 Hz 以下频段，并且取振动基板厚度hp=1.2 mm，根据式（24）和式（25）可得max{ax，ay}＜75 mm。为顾及结构的紧凑程度，方便曲面应用，本算例中选择的单元特征尺寸为ax=ay=38 mm。

其次，通过设计调整声学超材料单元中4 个共振结构的几何参数，可使其谐振频率均位于500 Hz 以下。本算例中每个单元包含的4 个共振结构的几何参数详见表1。

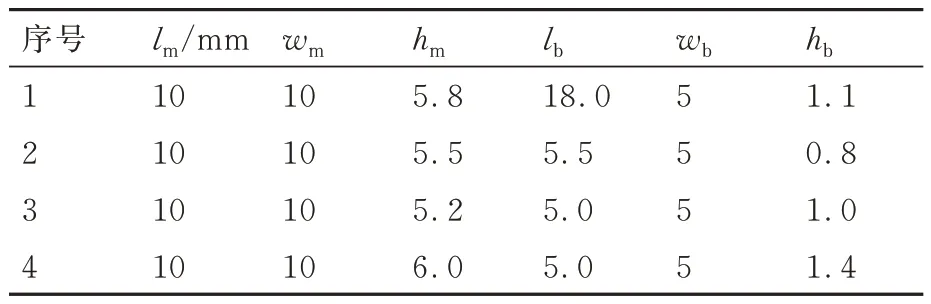
表1 每个单元包含的4 个共振结构几何参数Table 1 Geometric parameters of four resonant structures contained in each unit cell

每个单元包含的4 个共振结构定义为ABS 材料，其密度、杨氏模量和泊松比分别为1 050 kg/m3、2.5 GPa、0.35。本算例中，声学超材料的整体厚度为12 mm，其完整覆盖时与所附加振动基板的质量比为38%。

对于算例参数的声学超材料板，其能带结构如图4 所示。为便于比较，图4 中还给出了原始板即未附加声学超材料而仅振动基板的能带结构。通过比较这些能带结构，可以清晰地观察到500 Hz 以下频段声学超材料板所呈现的4 个完整带隙，分别为带隙1（106.8～110.7 Hz）、带隙2（203.9～210.5 Hz）、带隙3（307.7～316.9 Hz）、带隙4（436.9～455.8 Hz），在图4 中以阴影区域标注。

需要注意的是，声学超材料单元周期性地附加于振动基板还会引入Bragg 散射带隙。基于经典固体理论，布拉格散射带隙出现频率fB可以由单元特征尺寸来预测：

根据式（26）算得fB=2 018 Hz，远超所关注的频段范围，因此可以判断500 Hz 以下频段4 个带隙的产生归因于在亚波长尺度的主体结构中添加共振结构而产生的类Fano 干涉［46］而非Bragg 散射。

为了更直观地了解4 个带隙产生的物理机理，进一步借助商业有限元软件COMSOL Multiphysics 6.0 计算了各带隙上下限频率处的振型图案，如图5 所示。

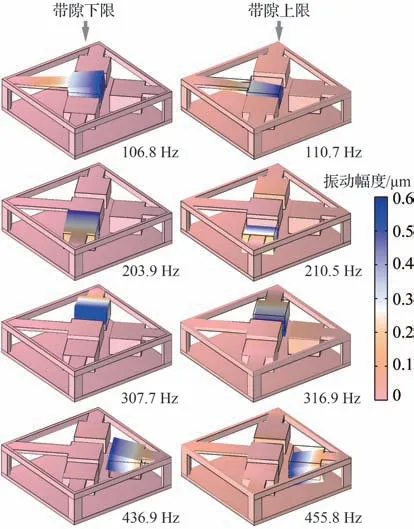
图5 4 个带隙上下限频率处的振型图案Fig.5 Mode shapes at the upper and lower frequencies of four bandgaps

由图5 可知，每一个带隙的产生均对应一个共振结构产生明显的局域共振现象，按照带隙出现频率由低到高，依次对应单元中的1～4 号共振结构发生谐振。因此，可以通过设计各个共振结构的谐振频率来调整各带隙的出现频率；在各带隙的下限频率处，振动基板几乎没有明显的运动，反而各个共振结构表现出显著的运动幅度。这种现象类似于振动结构上放置动力吸振器，在动力吸振器自身谐振时，振动结构中的能量被动力吸振器捕获，从而得到明显的振动抑制，亦即意味着带隙的开启；与此不同的是，在各带隙的上限频率处，振动基板与各个共振结构之间产生反向振动。这是由于声学超材料单元中每个共振结构的施加将原本单自由度系统的振动基板改造为相应的二自由度系统，而各带隙的上限频率便为各个二自由度系统的二阶共振频率，亦即意味着带隙的闭合。

4 小尺寸样件声学性能表征

基于带隙特性算例参数，进一步建立声学超材料结构的法向入射传声损失与振动传递函数的有限元计算模型。由3D 打印方式制作声学超材料样件，将其附加于小尺寸的均匀平直振动基板，分别开展法向入射传声损失试验和锤击激励振声试验，用以表征声学超材料的隔声增强性能和振声抑制性能，并验证有限元模型的有效性。

4.1 隔声增强性能与分析

建立如图6 所示的法向入射传声损失计算有限元模型。该模型基于COMSOL Multiphysics 6.0 的“声-结构相互作用”模块建立，包括振动基板和接触其上的声学超材料所构成的“固体力学”物理场以及入射和透射空气域所构成的“压力声学”物理场。2 个物理场通过“声-结构边界”处的力与位移连续性条件耦合关联。振动基板的边界条件设置为简支以模拟声阻抗管试验中样件的安装情况。平面声波通过入射空气域的端口垂直激励声学超材料结构后，一部分声能反射回到入射空气域，另一部分声能则透射进入透射空气域，入射和透射空气域的端口均设置为平面波辐射边界，以防止回波干扰；入射和透射空气域的侧壁设置为硬声场边界。提取入射波能量Wi及透射波能量Wt，可计算法向入射传声损失STLn，即

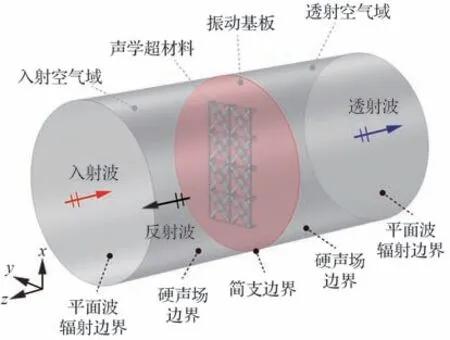
图6 法向入射传声损失计算有限元模型示意图Fig.6 Schematic diagram of finite element model for calculating normal incident sound transmission loss

相应的法向入射传声损失试验在特制的大口径声阻抗管中进行。该声阻抗管测试系统的搭建遵 循ASTM E2611-19 标 准［47］，可放置直径为225 mm 的圆形样件进行测试。如图7（a）所示，2 对压力场传声器（Brüel &Kjær，4938）通过安装底座分别侧嵌于入射声管和透射声管，2 个相邻传声器（M1与M2，M3与M4）之间的距离均为100 mm。该测试系统的有效测量频段为70～890 Hz。入射声管的末端放置扬声器（HiVi，SS8IIR），由功率放大器（YAMAHA，PX3）驱动发出20～1 600 Hz 频段范围的白噪声作为激励，透射声管的末端放置长度为1.5 m 的吸声尖劈，以尽可能减小回波干涉影响。试验样件照片如图7（b）所示，其中声学超材料包含2×4 个完整单元，振动基板为厚度1.2 mm的均匀铝板，两者的贴合采用双面胶（3M，55236）。样件的法向入射传声损失测试基于4 个传声器传递矩阵法［47-48］，4 个传声器的声压信号经数据采集仪（NI，USB-4431）获取后在计算机中进行频谱分析和传声损失计算。

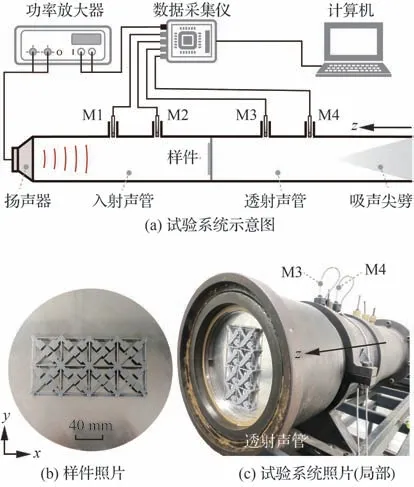
图7 法向入射传声损失试验装置Fig.7 Experimental setup for measuring normal incident sound transmission loss

图8 所示为样件法向入射传声损失的试验与仿真结果比较。作为参考，图8 中还给出了未附加声学超材料的原始板的试验与仿真结果。由图可知，无论对于原始板还是声学超材料板，仿真结果与试验结果的吻合程度都较好，表明了所建立的法向入射传声损失计算有限元模型的有效性。在所关注的500 Hz 频段内，声学超材料板对应曲线呈现出4 个明显的隔声尖峰，峰值增量均超过10 dB。需要说明的是，为了匹配峰值，将有限元模型中声学超材料与振动基板的接触面设置为弹性薄层边界（总弹簧常数为1.28×108Nm，弹簧损耗因子为0.15，附加重量为5 g），用以计及双面胶的使用对系统动态特性的影响。试验结果中4 个隔声尖峰对应频率分别位于104、211、325、457 Hz。注意到这4 个尖峰频率与仿真结果以及图4 所示的带隙计算频段之间存在稍许偏差，主要原因在于声学超材料样件由3D 打印方式制备，不可避免地存在几何尺寸偏离和材料成型非均匀度，由此造成了声学超材料单元包含的4 个共振结构谐振频率的偏差。尽管如此，图8 所示的结果依然表明，声学超材料施加于振动基板后能够在带隙频率附近显著提高振动基板的隔声性能。

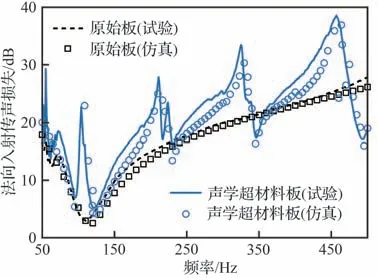
图8 法向入射传声损失试验与仿真结果比较Fig.8 Experimental and simulated results comparison of normal incident sound transmission loss

需要指出的是，声学超材料施加于振动基板后还会在某些频段造成隔声性能退化的现象，如图8 所示的231、346、492 Hz 频率附近。造成这种现象的原因在于声学超材料的施加在这些频段导致了二自由度系统的二阶共振，从而导致透声增强。可尝试通过增加声学超材料的结构阻尼来改善这些频段处的隔声性能，但增加声学超材料的结构阻尼会一定程度上削弱带隙效应［49］，因而需要折中取舍。

4.2 振声抑制性能与分析

接下来采用冲击力锤作为激励，测试声学超材料附加于均匀平直振动基板后对其振动传递与振声辐射特性的影响。

如图9（a）所示，在半消声室测试环境中，使用尼龙细线将振动基板（长度为500 mm，宽度为500 mm，厚度为1.2 mm 的铝板）自由悬挂。在振动基板背面安装一枚轻质加速度传感器（PCB Piezotronics，352C22），用以测量该响应点处的振动响应。该加速度传感器重量仅为0.5 g，相对于振动基板而言足够轻，故可以忽略其附加重量对振动基板模态特性的影响。在振动基板正面距离其中心200 mm 处放置一个自由场传声器（BSWA，MPA416）获取该点的辐射声压。使用冲击力锤（Brüel &Kjær，8206）垂直敲击振动基板背面的激励点。锤击激励点和加速度响应点对称设置在振动基板的对角，与板的2 个相邻边缘分别相距65 和55 mm。每次测试过程锤击3 次，做平均。3 路信号，即力、加速度和声压，由数据采集仪（NI，USB-4431）记录并在计算机中进行频谱分析，获得相应的振动传递函数（加速度/力）和振声传递函数（声压/力）。振动或振声传递函数的幅值越小，表明声学超材料对振动基板的振动传递或振声辐射的抑制作用越明显。图9（b）和图9（c）分别示出了原始板和附加声学超材料后的样件照片。声学超材料样件与振动基板之间通过双面胶（3M，55236）贴合。整个振动基板共附加15 块包含2×4 个完整单元的声学超材料样件，声学超材料的附加总重量与振动基板的重量比为35%。

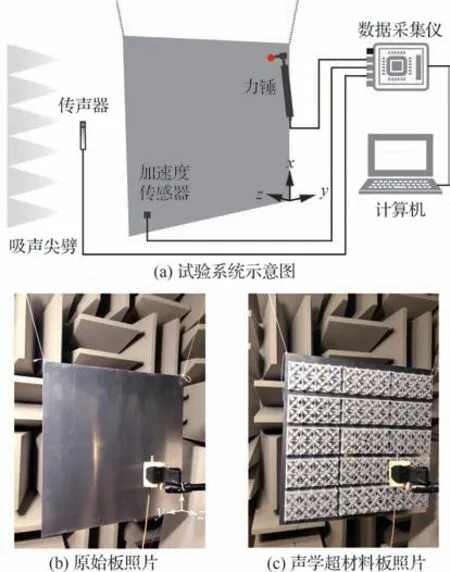
图9 锤击振声试验装置Fig.9 Experiment setup for vibroacoustic measurements by using hammer excitation

考虑到振声耦合的计算复杂度，这里仅建立如图10 所示的振动传递函数计算有限元模型。该模型基于COMSOL Multiphysics 6.0 的“结构力学”模块建立。振动基板的边界条件设置为自由以模拟锤击试验中样件的安装情况。声学超材料与振动基板的接触面同样设置为弹性薄层边界，包含的动力学参数同法向入射传声损失计算有限元模型。

图10 振动传递函数计算有限元模型示意图Fig.10 Schematic diagram of finite element model for calculating vibration transfer function

试验获得的原始板与声学超材料板的振动传递函数幅值比较如图11 所示。在所关注的500 Hz 频段内，声学超材料可以明显抑制振动基板中的弯曲波传播，可以清晰地辨别出4 个振动传递低谷，对应的振动传递函数幅值下降幅度均超过10 dB，4 个低谷频率分别位于104、221、325、457 Hz（图11 中箭头指示），与图8 所示的法向入射传声损失曲线的4 个尖峰频率一致。因此，可以判断这4 个振动传递低谷的出现同样归因于声学超材料单元产生的4 个局域共振带隙，在带隙频率范围内原本振动基板中可自由传播的弯曲波能量被局限在声学超材料单元中的4 个共振结构，从而使得振动基板具有非常低的响应幅度。

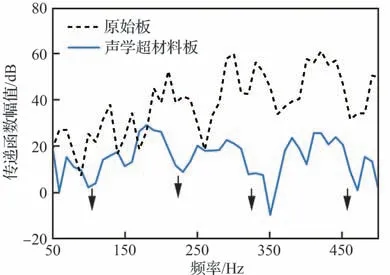
图11 振动传递函数幅值试验结果Fig.11 Magnitudes experiment results of vibration transfer function

图12 所示为振动传递函数幅值的试验与仿真结果比较。其中，图12（a）和图12（b）分别对应原始板和声学超材料板结果。由图12 可见，无论对于原始板还是声学超材料板，仿真结果均可以较好地吻合试验结果的峰谷趋势，表明了所建立的振动传递函数计算有限元模型的有效性。

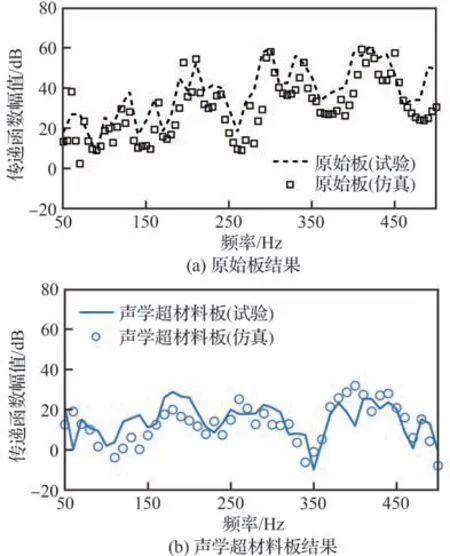
图12 振动传递函数试验与仿真结果比较Fig.12 Experimental and simulated results comparison of vibration transfer function

借助所建立的振动传递函数计算有限元模型，可以直观地观察所关心频率处的振动响应衰减情况。图13 中比较了简谐力激励幅值为1 N情况下的原始板与声学超材料板在104 Hz（对应图11 所示的第1 个低谷频率）处的法向位移幅值仿真结果。可以发现，在安装声学超材料后，围绕激励点附近的声学超材料中标号为1 的共振结构产生了明显的局域共振现象，从而显著抑制了传递至响应点的振动位移幅度。这一现象与图5分析的带隙产生机理一致。

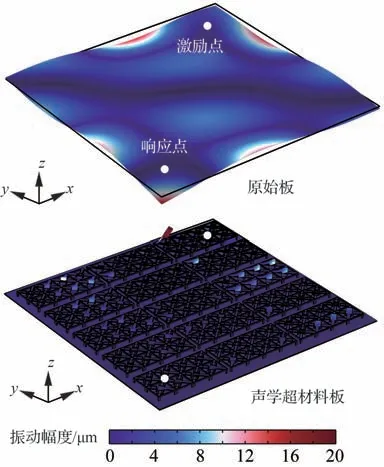
图13 原始板与声学超材料板在104 Hz 处的法向位移幅值仿真结果比较Fig.13 Comparison of normal displacement amplitudes between pristine plate and acoustic metamaterial plate at 104 Hz

图14 所示为原始板与声学超材料板的振声传递函数幅值的试验结果比较。由图可知，声学超材料的附加能够明显降低振动基板在所关注的500 Hz 频段内的振声辐射能力。图14 中箭头指示的频率等同于图11 中指示的振动传递函数的4 个低谷频率。可以看到，声学超材料的附加对振声传递函数幅值的降低主要体现在104、221、325 Hz 附近的前3 个带隙，而在457 Hz 对应带隙处并未有效体现。其原因主要在于：一方面，振动基板在457 Hz 临近反共振模式，振动基板本身整体的振动幅度便较低，而声学超材料的附加主要以抑制振动基板响应幅度的方式降低振声辐射，因此反共振模式附近的效果便无法有效体现；另一方面，声学超材料此时本身恰处于局域共振模式，剧烈振动的共振结构还会辐射部分声能造成声辐射增强。

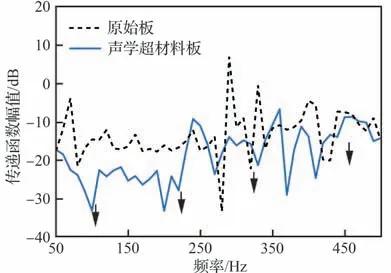
图14 振声传递函数幅值试验结果Fig.14 Magnitudes experiment results of vibroacoustic transfer function

5 大尺寸壁板试验效果

由于直升机舱壁为大尺寸的加筋曲板结构而非小尺寸的均匀平直板结构，有必要进一步开展声学超材料附加于大尺寸曲面加筋壁板的降噪效果试验验证。

5.1 扩散场入射传声损失试验

如图15 所示，测试用的壁板结构为单一曲率矩形加筋板，轴向长桁和周向隔框作为加强筋铆接于蒙皮之上。长桁、隔框和蒙皮分别由2、1.5、2.5 mm 厚的航空级铝材制成。壁板总重量为20.6 kg，其投影长度和宽度分别为1 504、1 185 mm，曲率半径为1 026 mm，等效面密度约为11.6 kg/m2。使用混凝土制成的框架将试验壁板夹持固定于测试窗口中，图15 所示的虚线范围内部为有效测试区域。在框架-试验壁板之间以及框架-测试窗口之间使用硅酮胶进行声学密封，避免漏声对试验结果造成影响。

图15 大尺寸试验壁板结构示意图Fig.15 Schematic of large-scale sidewall panel for experiments

在混响-全消声室中开展扩散场入射传声损失测试，试验系统示意图如图16 所示。根据式（28）计算样件的扩散场入射传声损失Rd：

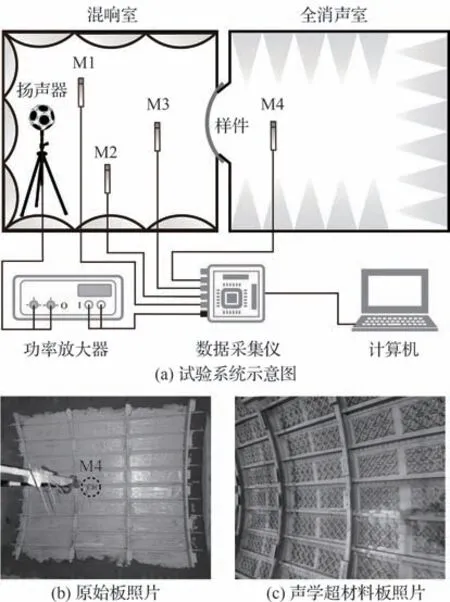
图16 扩散场入射传声损失试验装置Fig.16 Experimental setup for measuring diffuse-field incident sound transmission loss

式中：为由位于混响室不同位置的3 个自由场传声器M1～M3（Brüel &Kjær，4189）获得的平均声压级；LA为消声室中距离样件中心500 mm处的自由场传声器M4（Brüel &Kjær，4189）获得的单点声压级。混响室中的扬声器（Brüel &Kjær，4292-L）由功率放大器（Brüel &Kjær，2716-C）驱动产生50～5 000 Hz 频段的白噪声激励。4 个自由场传声器获得的声压信号由数据采集仪（Brüel &Kjær，3560C）记录并送至计算机进行频谱分析与计算。

图16（b）所示为未附加声学超材料样件的原始板照片。该试验构型作为参考基准，在试验开始和结束时均进行测量，以验证测试结果的可重复性和数据一致性。对于每1/3 倍频程，2 次测试结果之间的最大差值应低于0.5 dB。图16（c）所示为附加声学超材料样件的声学超材料板照片，使用双面胶（3M，55236）将声学超材料样件与试验壁板进行贴合。可以看到，声学超材料样件分布在由长桁和隔框间隔而成的蒙皮区块（该区块具有沉槽，实际蒙皮厚度减薄至2 mm）。整个试验壁板上共附加了48 块包含2×4 个完整单元的声学超材料样件，附加总重量为试验壁板的2.3%。

原始板与声学超材料板的扩散场入射传声损失试验结果比较如图17 所示。对于原始板结果，在125 和900 Hz 频段出现了2 个明显的隔声塌陷，分别对应原始板各蒙皮区块的一阶弯曲共振和原始板整体的环向共振，其中环向共振频率fr可由式（29）粗略估计［26，50］：

图17 扩散场入射传声损失试验结果Fig.17 Experimental results of diffuse-field incident sound transmission loss

式中：r为壁板的曲率半径。由式（29）算得fr=836.7 Hz，与试验结果的吻合程度良好。

当附加声学超材料以后，在500 Hz 以上频段，声学超材料板对应的扩散场入射传声损失均明显高于原始板构型，平均隔声性能提升可达6 dB。在所关注的500 Hz 以下频段，除250 Hz的1/3 倍频程中心频段以外，附加声学超材料均有利于提高试验壁板的扩散场入射隔声性能，但提升量并不如声阻抗管中测试的法向入射传声损失结果那样明显，仅可粗略辨别200、315、400 Hz 的1/3 倍频程中心频段对应的隔声增强现象。可能存在以下2 个方面的原因：①低频激励引起的壁板振动在纵向和周向的多个蒙皮区块上存在较高的相关性，不能仅从抑制蒙皮区块振动的角度考虑整体壁板的隔声增强，还应该兼顾长桁和隔框区域的处理；②在低于环向共振频率的低频段，壁板结构刚度占主导地位［51-52］，试验时固支边界的施加已经显著增加了整体结构刚度，而声学超材料的附加无法进一步提升壁板的结构刚度，因而未能获得理想的隔声增强效果。尽管如此，试验结果仍然表明声学超材料在提高复杂结构壁板的扩散场入射隔声性能方面起到正面作用。

5.2 振动传递与振声辐射特性试验

在所搭建的扩散场入射传声损失试验系统基础上，将扬声器和M1～M3 号传声器撤除，激励改用激振器施加，如图18（a）所示，可将试验系统改造为激振器振声试验。激振器（PCB Piezotronics，2007E）推杆端部安装力传感器（PCB Piezotronics，208C01）用以获取壁板背侧激励点F 处的输入力，并在壁板背侧放置3 个加速度传感器（PCB Piezotronics，352C22）用以拾取壁板A1～A3 位置处的加速度振动响应。图18（b）和图18（c）分别给出了激励点与响应点位置对应的壁板正侧示意图和实际背侧照片。需要说明的是，激励点位于长桁和隔框的交汇点，符合直升机舱壁实际承载动力装置的安装节点位置；3 个响应点则均位于不同的蒙皮区块中心，是壁板原本振动和声辐射较为强烈的部位。

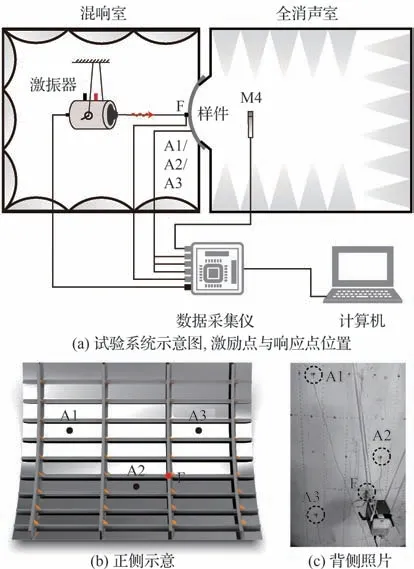
图18 激振器振声试验装置Fig.18 Experiment setup for vibroacoustic measurements by using shaker excitation

图19 分别为原始板与声学超材料板在A1～A3 3个位置处的振动传递函数幅值比较。可以看到附加声学超材料后，壁板在500 Hz 以下频段3 个位置处的振动响应幅度均得到了明显地抑制，尤其是图中箭头指示的4 个带隙频率（箭头指示频率同图11）附近，振幅下降幅度可达10 dB。这意味着尽管振动基板由简单的均匀平直板变为更为复杂的弯曲加筋板，但由附加的声学超材料带隙引起的振动衰减现象依然能够明显体现。需要强调的是，如此优异的抑振效果是在附加的声学超材料总重量仅为试验壁板重量的2.3%情况下获得的，从而充分证明了多带隙声学超材料在抑制复杂壁板结构振动方面的潜力。

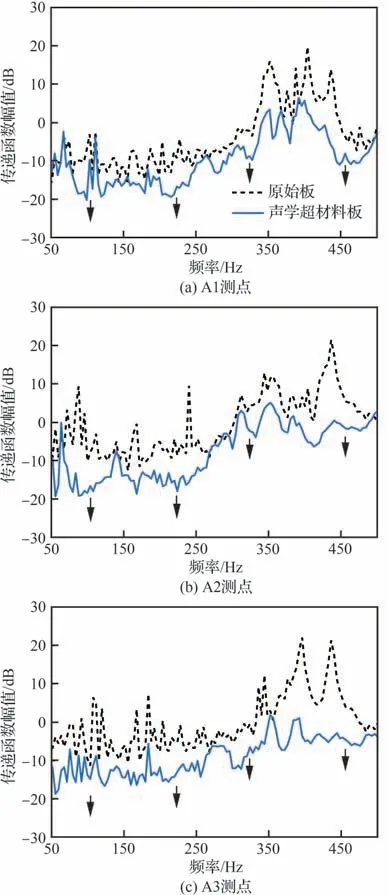
图19 振动传递函数幅值试验结果Fig.19 Magnitudes experimental results of vibration transfer function

原始板与声学超材料板的振声传递函数幅值比较如图20 所示。从图中观察到，声学超材料的附加可以较为明显地在150 Hz以上频段降低试验壁板的振声辐射能力，能够粗略辨别221、325、457 Hz带隙频段对应的声辐射抑制现象。

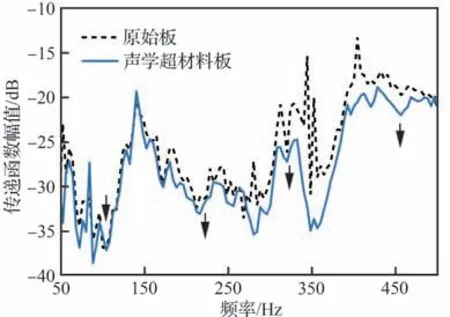
图20 振声传递函数幅值试验结果Fig.20 Magnitudes experiment results of vibroacoustic transfer function

另外需要注意的是，因为长桁和隔框区域并未附加声学超材料，故无法有效抑制这些区域振动产生的声辐射。这启发我们在实际应用时不仅仅需要在蒙皮区域附加声学超材料，还需要对长桁和隔框区域进行额外的声学处理，例如贴敷定制结构形式的声学超材料或约束层阻尼。此外，声学超材料处于局域共振模式而造成的潜在声辐射增强问题值得后续深入研究。

6 结论

1）提出了一类低频多带隙声学超材料，能够在直升机舱内噪声所关注的500 Hz 以下频段呈现4 个完整带隙，每一个带隙的产生对应声学超材料单元包含的一个共振结构的局域共振，可以通过设计各个共振结构的谐振频率来调整各带隙的出现频率。

2）在小尺寸均匀平直的振动基板上开展的法向入射传声损失试验与锤击激励振声试验结果均表明，理论预测的声学超材料带隙频率范围与实测的隔声提高区和传递函数幅值衰减区较为吻合，验证了理论计算结果的正确性。声学超材料对振动基板的峰值隔声增加量以及振动和振声传递函数幅值的抑制量均超过10 dB，表现出了优异的降噪性能。

3）在大尺寸曲面加筋壁板上开展的扩散场入射传声损失试验与激振器激励振声试验结果均表明，尽管附加的声学超材料总重量仅为试验壁板重量的2.3%，由声学超材料带隙引起的隔声增加与振动衰减和声辐射抑制现象依然能够明显体现，证明了提出的多带隙声学超材料在对复杂结构壁板降噪应用方面的潜力。