目标气动特性下动力翼参数影响分析与优化

孙蓬勃，周洲，李旭，王科雷

西北工业大学 航空学院，西安 710072

近年来，随着环保要求和运输效率需求的提升，分布式电推进技术受到了关注，并在飞行器的设计中逐步得到了应用发展。以XV-24［1］和Lilium［2］为代表的分布式动力翼（Distribution-Propulsion-Wing，DPW）飞行器将涵道动力与机翼高度融合，形成了复杂的气动-推进耦合关系，已经打破了传统的飞发匹配概念。新型推进方式的变革体现了飞行器设计从单一动力研究到飞行器总体、动力、气动等技术集成研究的变化，为航空科技发展提供新的方向［3］。此类构型的推进单元本身成为升力产生面的一部分且动力装置改变了机翼表面的流动，从而显著影响整体的气动力特性。这为分布式动力翼飞行器带来了广阔的设计空间，但也因为传统的基于干净来流的翼面设计方法失效，带来了极大的设计困难。因此，深入开展分布式动力翼的气动设计研究对于真正实现其优势具有重要的工程意义和学术价值，对此许多学者开展了研究。

Kerho［4-5］针对一种TeDP（Turboelectric Distributed Propulsion）验证飞机开展了设计研究，对二维剖面外形的涵道唇口形状和涵道安装角进行了设计研究，并进一步开展了翼段三维设计与实验研究。Schiltgen 等［6］和Papathakis［7］分 别对split-wing 这样一种机翼完全由动力充当的构型进行了数值模拟，结合进出口宽度、唇口曲率等参数进行了二维外形建模与设计分析；Lauer和Ansell［8-9］用贝塞尔曲线对分布式电推进构型的二维剖面进行了参数化建模与优化设计。夏济宇等［10］结合二维理论模型与工程经验模型提出了一种适用于矢量电推进系统的气动-推进耦合模型。Guo 和Zhou［11］将分布式涵道单元内外流分开考虑，基于超椭圆参数化方法对进排气道外形进行了优化推进效率的设计。王科雷等［12］依次对动力翼二维剖面翼型、动力单元翼段、分布式动力翼整体的动力/气动综合特性进行了数值研究，梳理了分布式动力翼内外流耦合与其二维-单元-整体特性之间的内在联系。张星雨等［13］通过地面试验结合数值模拟的方法对分布式电推进技术验证机的气动性能及其气动-推力耦合关系开展了研究。

飞行器设计通常需要满足给定的升力和力矩特性。然而基于目前的研究可以看出，已有的动力翼研究多关注其自身的特性分析和优化设计，但对如何将动力翼设计收敛到所需的目标气动特性的研究较少。如能在满足气动特性目标值的前提下发挥动力翼的优势，则更具有实际工程意义。具体可从以下3 个方面展开讨论：

1）从设计难度上看，相比常规机翼，动力翼的升力和俯仰力矩等气动特性都有显著改变；所受影响因素较多，不同情况下的气动特性变化过程相对复杂。这增加了动力翼气动设计的收敛难度，如何使动力翼设计方案能够契合所给的设计目标和约束成为需要研究的方向。

2）从设计思路上看，分布式动力翼具有典型的单元周期特性及动力壁面的类翼面特性。从文献［11-12］中对动力翼特性规律的认识以及设计逻辑的研究来看，可以根据内外流与升力、推进（阻力）特性之间关系对动力翼设计进行拆分。取动力翼剖面形状来进行升力和力矩特性调控，取进排气道进行推进（阻力）特性调控，二者之间相互耦合，但又相对独立。所以首先开展动力翼剖面二维设计研究是有重要作用的，其结果可直接指导动力翼外流面的形状设计，并可进一步作为进排气道三维形状设计的基础，以降低直接开展三维设计所需的计算迭代次数，从而提高动力翼的设计效率。此外由于其本身较快的计算和设计收敛速度，也可用于动力翼方案的快速对比评估。

3）从设计方法上看，多数对于分布式动力翼飞机的设计研究均基于传统的参数优化方法，在考虑发动机影响的条件下进行优化并收敛到目标，面对较多的变量参数和复杂流动机理，这种方式难以准确收敛到所需的气动特性目标值，且计算次数较多，计算量极大。所以相比正向的直接优化逐步接近目标气动特性的方式，动力翼的反设计成为值得探索的方法。

因此面向分布式涵道动力机翼的设计，基于上述思路，本文通过一种以弦向环量分布为目标的动力翼二维反设计方法开展了动力翼二维形状的反设计研究，分析了相同升力和俯仰力矩前提下，涵道壁位置与涵道壁弦长对反设计外形及其气动性能的影响，并进一步开展了分布式动力翼剖面二维外形优化反设计，以期采用反设计方法实现给定气动特性目标下分布式动力翼剖面形状的快速设计，为动力翼的进一步三维设计提供基础，并用于方案的快速对比评估和优化。

1 动力翼二维反设计方法

反设计方法通过求解空气动力学反问题的方式来使设计外形达到期望的气动特性，具有计算效率高、针对性强等特点［14］。然而，传统的翼型反设计方法主要针对均匀远场来流，当设计对象是动力翼剖面这种内外流深度耦合的构型时，仍需发展相应的气动反问题求解方法。升力和力矩特性是典型的翼型设计目标，而如图1 所示，图中x为弦向位置，γ为环量，翼型的弦向环量分布（即弦向升力分布）是对升力和力矩的表征，所以可将其分解到动力翼剖面的各部分作为反设计目标；在此基础上通过参数化表达目标环量分布和其他构型参数，可以进一步实现动力翼反设计方案的优化。

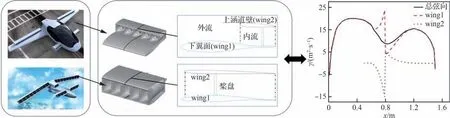
图1 分布式动力翼二维反设计Fig.1 2D inverse design of distribution-propulsion-wing

为了给出分布式动力翼反设计的完整流程并提高反设计效率，主要介绍以下两点的推导和方法：

1）考虑桨盘等其他部件诱导影响的翼型理论推导与初步反设计流程。

2）反设计修正方法。

在反设计迭代的过程中，虽然是二维流场计算，但因迭代次数一般较多，直接采用CFD 方法仍然是比较耗时的。因此在迭代初期使用快速高效的势流方法，结合反设计方程推导，有助于快速收敛到目标解附近，在迭代后期再基于CFD计算进行进一步修正。

1.1 初步反设计

1.1.1 翼型理论推导

根据文献［15］，对于二维薄翼型，其气动特性可通过中弧线上的点涡环量分布来描述，其任意一点x0处的边界条件为

式中：左侧为来流在中弧线上当地位置的法向分量，右侧为弦向各ξ处点涡对当地法向诱导速度之和；V∞为来流速度；α为翼型迎角；y′(x0)为当地中弧线斜率；c为翼型弦长。

对于动力翼二维剖面当中的一个翼型，将桨盘及其他部件的诱导速度考虑进来作为此翼型背景来流的一部分，在中弧线任意一点有叠加了桨盘等其他部件诱导速度后的局部流动迎角αlocal(x)及局部速度Vlocal(x)。

进一步将弦向环量γ分布由傅氏级数表达：

式中：θ为弦向各处坐标ξ的三角函数变换，相应的坐标x0对应为Θ；A0、An为系数。

将式（2）代入式（1）右侧，可得

通过式（3）可以看出，翼型沿弦向的环量γ分布可视为与中弧线斜率y′和当地来流速度Vlocal相关的函数。如果在翼型上，从前缘到后缘，布置N个控制点，通过给定在各控制点的目标环量值γi(i=1，2，…，N)并计算流场得到各控制点处的当地速度Vlocal，将中弧线斜率值作为求解对象，可在任意控制点Θ处将式（3）代入式（2）：

将式（4）中的积分离散化，提取出y′的系数并将各控制点处构造的方程组写为矩阵形式：

式中：θi为各点的三角函数坐标；(Δθ)j为第j处θ区间量Δθ的大小。

根据式（6）的推导，可以看到式（5）中矩阵A是奇异的（最后一行对应后缘点处的等式，此时θi=π，所以此行值均为0），因而构建方程组时应去除掉过于接近后缘的几个点，考虑到一般翼型弯度变化的连续性，这不会产生过大的误差，反而带来了求解上的便利。采用伪逆法求解式（6），便可以得到桨盘等其他部件影响下的薄翼型中弧线形状。

1.1.2 翼型厚度影响分解

实际翼型设计过程中，厚度带来的影响经常是不可忽略的。文献［16］中，假设流动是不可压和有势的，一个有厚度翼型所对应的环量分布可分解为如图2 所示的两部分。Part1 表示具有对应厚度分布的对称翼型在该迎角下的环量分布，Part2 表示对应弯度分布的薄翼型在0°迎角下的环量分布。所以需首先计算Part1 中对称翼型的弦向环量分布，并在反求Part2 薄翼型弯度分布时，在目标环量分布的给定中将这一部分去掉。

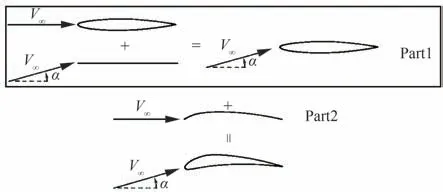
图2 翼型厚度影响分解Fig.2 Decomposition of airfoil thickness influence

但是针对所研究的对象，由于存在桨盘等其他部件的诱导速度，翼型表面各处的背景来流是不同的。所以在计算Part1 对称翼型弦向环量分布时，采用二维涡格法［16］把实际翼型表面各处的来流速度矢量转移给对称翼型上对应表面位置的涡格，作为其速度边界条件（图3）。

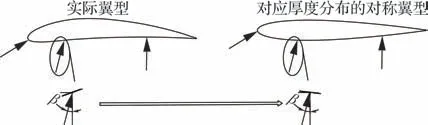
图3 对称翼型的速度边界条件Fig.3 Velocity boundary conditions of symmetrical airfoil

1.1.3 二维自由尾迹涡格法

为了能够对分布式动力翼构型进行快速计算迭代并获取桨盘等其他部件对所求翼面各处的诱导速度，采用自由尾迹涡格法求解。李旭等［17］参考Shollenberger［18-19］的求解思路，基于自由流线模型，利用涡面对射流进行建模，结合一阶涡格法，建立了二维自由尾迹涡格计算方法。如图4 所示，以离散涡面加半无限长涡面表征二维桨盘喷流，其中离散段用来迭代受物面影响的自由尾迹；同时也将翼型离散为涡面。详细的迭代计算过程可参考文献［17］。

图4 翼面与桨盘喷流的涡面Fig.4 Vortex surface of airfoil and disk jet

1.1.4 初步反设计流程

图5 显示了分布式动力翼二维剖面初步反设计流程，主要包括以下6 个步骤：

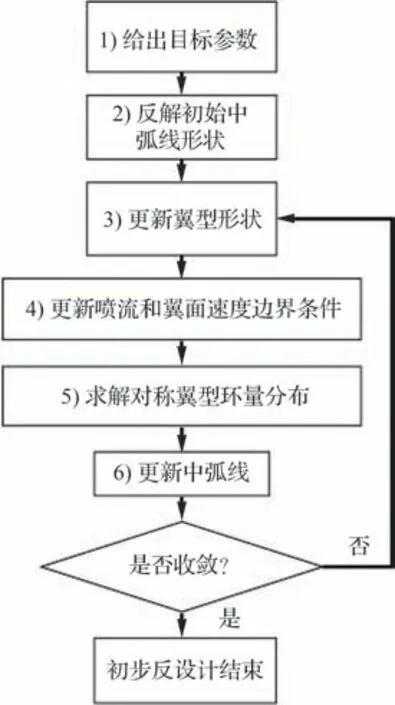
图5 初步反设计流程Fig.5 Primary process of inverse design

1）给出桨盘的推力、半径、弦向位置，翼型弦长，来流速度，并给出各翼面目标环量弦向分布。初始的翼型中弧线形状可以是无安装角的直线，两翼型之间保持一定高度差以容纳桨盘。

2）初始的桨盘喷流可以是平直的直到无限远，通过涡格法计算翼型中弧线上各处所受的诱导速度，并通过式（5）计算得到翼型中弧线形状。

3）基于给定的翼型厚度分布，得到翼型形状。由于翼型弦向环量分布是由傅里叶级数拟合得到的，所以当阶数给定不合适的时候，容易出现过拟合的问题，表现为求解得到的翼型形状的振荡（图6），这会严重影响到后续求解的收敛性；所以此处预先通过CST（Class Shape Function Transformation）拟合的方式［20-21］对翼型进行了光顺，从而提高设计程序的鲁棒性；光顺方法为分别光顺上下表面，求均值得到新的中弧线，再通过给定的厚度分布生成新的翼型外形。进一步垂直平移翼面，使得桨盘能被容纳在给定的位置。

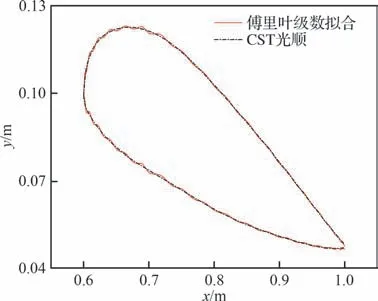
图6 CST 光顺翼型Fig.6 CST airfoil smoothing

4）结合喷口内壁形状更新桨盘喷流离散涡面的初始形状，并通过自由尾迹涡格法迭代求解得到翼型表面各处的当地来流速度矢量。

5）由给定的厚度分布生成对称翼型，将步骤4）中的翼型表面各处局部速度矢量赋给对称翼型作为边界条件，由涡格法计算对称翼型表面压力分布，进而得到对称翼型的弦向环量分布。

6）将对称翼型的弦向环量分布从目标环量分布中去除，通过式（5）计算更新翼型中弧线形状。返回步骤3），直到相近两次迭代得到的翼型中弧线形状均方误差小于10-5，则认为初步反设计收敛。

1.2 修正方法

1.2.1 CFD 方法验证

使用商业数值模拟软件FLUENT 进行CFD计算，采用动量源方法（Momentum Source Method，MSM）模拟桨盘推力对来流的加速作用，采用k-ω剪切应力传输（Shear Stress Transport，SST）湍流模型，求解RANS（Reynolds-Averaged Navier-Stokes）方程，数值计算过程中空间离散采用二阶迎风MUSCL（Monotone Upstreamcentered Scheme for Conservation Laws）插值的Roe 格式，时间离散与推进则采用隐式AF（Approximate Factorization）方法。

首先针对NASA 涵道风扇［22］采用动量源方法进行计算分析并与实验结果进行对比。如图7所示，将实验中的桨盘拉力值以对应大小的动量源的形式代替，最后比对30 m/s 来流工况下的总拉力T，边界条件设置与实验条件相一致，结果见表1，可见在不同网格数量下，MSM 计算结果与实验值相对误差η最大为3.37%，最小为1.28%。通过表1 结果对比，能够排除网格数量对计算结果的影响，并且说明动量源方法的有效性。

表1 MSM 不同数量网格计算结果Table 1 Calculation results of MSM with different grid numbers

图7 MSM 计算网格Fig.7 Mesh of MSM calculation

另外，也针对第2～4 节中的NLF（1）-0416 翼型经过网格无关性验证后给出二维CFD 计算结果，总网格数约为12 万。计算工况为来流马赫数0.1、雷诺数4×106、迎角1°［23］。翼型表面压力分布如图8 所示，可见与实验结果基本一致。

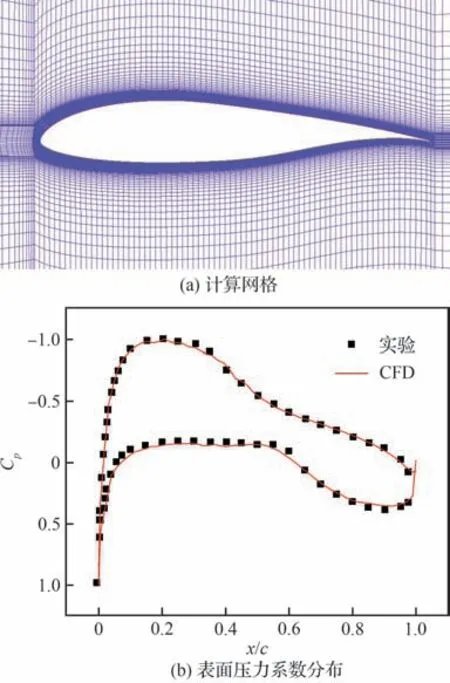
图8 NLF（1）-0416 二维计算网格与Cp分布Fig.8 2D mesh of NLF（1）-0416 and Cp distribution

通过对表1 和图8 的分析，能够说明所用CFD 方法的准确性。

1.2.2 CFD 修正

由于在初步反设计流程中采用的是快速势流方法，无法考虑黏性效应且准确性受涡核半径等参数设置的影响，与实际流动存在一定偏差，所以还需通过CFD 计算来对反设计进行校核修正。如图9 所示，在初步的反设计迭代收敛后，对设计结果进行二维CFD 计算，得到实际的弦向环量分布（图9（a）中的初步反设计）并与目标弦向环量分布进行对比，通过将差量叠加修正进初步反设计的设计目标，反复进行若干次初步反设计的方式（图9（b）），使得初步反设计的实际结果最终与目标弦向环量分布接近一致。

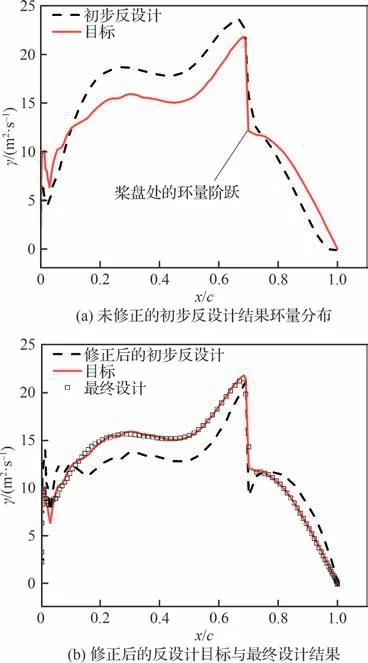
图9 CFD 修正示例Fig.9 Example of CFD correction

1.2.3 Modified Garabedia-Mcfadden（MGM）修正

由于傅里叶级数拟合是对弦向环量分布的整体性描述，因此经过1.1 节和1.2.2 节迭代得到的设计结果，某些时候在局部环量梯度较大的位置（尤其是桨盘附近和前缘）或所取阶数n不合适时，仍可能与目标环量分布存在少量差距，这时可使用MGM 对设计结果做进一步微调。

Malone 等［24］基于线性小扰动理论，改进得到了MGM 方法用于翼型反设计；其思想是将翼型表面压力系数与气动外形参数结合，得到计算、目标压力系数与翼型表面坐标相关联的MGM 方程。但由于设计对象是翼型中弧线形状且目标为环量分布，翼型表面目标压力分布是未知的，所以给出保持厚度分布、只修正中弧线形状的MGM 方程（环量等效于翼型上下表面压强差，所以相当于上下表面各自的压力分布修正叠加，因而公式形式与常规MGM 方程一致）：

式中：R为残差，R=γt-γc，其中γc和γt分别为计算环量值与目标环量值；x为翼型弦向坐标；F0、F1、F2为常值系数，用以实现稳定迭代，它们后面的项分别代表中弧线各点高度位置的修正量ΔY及其对x的一阶和二阶导数。基于文献［23］中的求解方法对中弧线进行迭代微调，使动力翼环量分布与目标分布的平均相对误差（Average Relative Error，ARE，进一步下降，直到收敛。第2～4 节在反设计研究中，权衡气动特性的收敛精度和迭代计算次数，取收敛标准为ARE ＜0.06。

2 反设计示例

验证第1 节介绍的反设计方法的有效性。为尽量保证所给目标分布的合理性，同时也为研究相同升力和力矩特性下动力翼相比传统翼型的优势并进一步结合研究背景，以弦长1.5 m 的通航飞机典型研究翼型NLF（1）-0416（图10）的弦向环量分布为目标，反设计与其物面升力和力矩一致的动力翼二维外形。给出动力翼单元剖面中wing1（下翼面）、wing2（上涵道壁）、桨盘的弦向位置和长度，如图11 所示（(xd-x1)/(x2-x1)=0.3）。动力翼剖面的两翼型厚度分布形式与NACA 四位数翼型相一致，最大相对厚度均为8%。桨盘半径r=0.15 m，推力T′=400 N（T′为二维等效推力，其与三维圆桨盘单元推力之间的关系详见文献［4］）。远场来流速度V∞=60 m/s，大气参数按海拔1 000 m 给定，密度ρ=1.111 kg/m3，迎角α=0°。

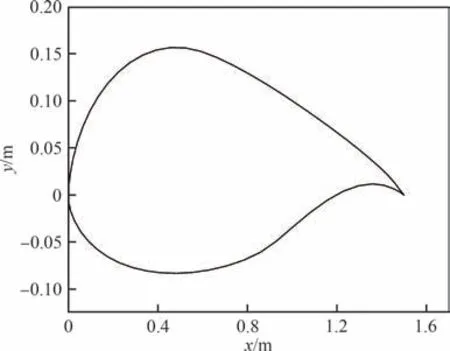
图10 NLF（1）-0416（弦长为1.5 m）Fig.10 NLF（1）-0416（chord is 1.5 m）

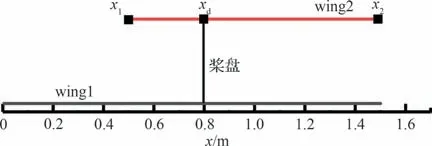
图11 部件位置Fig.11 Part location

如无特别说明，气动力系数的参考长度均为总弦长。此外，实际上动力翼俯仰力矩除受环量分布影响，也与参考点和两翼型物面阻力矢量及桨盘推力矢量的位置关系有关，把评估俯仰力矩时的参考点放在桨盘中心线上，尽量减少力矩对比时桨盘推力线和壁面阻力对俯仰力矩的影响；参考点弦向位置在1/4 总弦长处。

对于如何给定动力翼剖面翼型的目标环量分布形式，参考文献［24］对翼型表面压力分布的描述思路来进行。文献［24］将翼型上/下表面的压力分布形式按激波阶跃位置分为前加速段和后减速段。类似的，可将动力翼上部涵道壁的翼型环量分布按桨盘处的环量阶跃分为前部桨盘抽吸段和后部恢复段两部分。前部环量分布由于受翼型本身形状变化和桨盘抽吸的影响，可能存在多个极值点，所以通过多项式的形式描述；而考虑到桨盘后的内流面单侧压强较高，且翼型内外压强差（环量）向后缘一般单调恢复至0，所以参考文献[24]指数函数的方式描述后部恢复段的环量分布形式。需要说明的是这种描述方法不一定能涵盖所有环量分布形式，这里仅为一类较符合实际的形式，用以开展反设计方法的验证工作。在实际设计时，可根据具体情况和经验制定不同的目标环量分布形式。

结合上述讨论，在反设计示例中，wing1 和wing2 的弦向目标环量分布按如下方式给出：首先通过CFD 计算得到基准翼型的弦向环量分布，然后将上涵道壁wing2 环量分布形式表示为

式中：γd为桨盘前处的wing2 当地环量值，考虑到桨盘抽吸一般会使wing2 前部下表面压力低于外表面，所以γd一般为负数，取γd=-15 m2/s；Δγ=T/(2rρV∞)为桨盘前后压力阶跃所对应的环量值阶跃；n1、n2、n3为分布控制系数，在对比不同系数取值设计结果的基础上，可得到相对合理的系数取值范围，取n1=0.7、n2=5、n3=5。将目标翼型与wing2 的目标环量分布相减，得到下部翼面wing1 的目标环量分布。目标翼型及其分解为wing1 和wing2 的弦向环量分布如图12 所示。

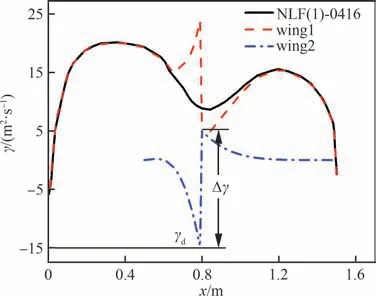
图12 目标环量分布Fig.12 Target circulation distributions

图13 给出了经过8 轮CFD 修正初步反设计之后的环量分布，可见反设计得到的弦向环量分布与给定的目标基本接近，但在桨盘和前缘附近仍有一些差距，这使得此时的环量分布平均相对误差仍比较高。进一步使用MGM 方法进行修正，F0、F1、F2分别取值为4、2、2。经过另外8 次结合CFD 计算的MGM 修正后，最终设计得到的环量分布与外形如图14 所示，图中CL为升力系数，Cm为俯仰力矩系数。可见经过外形微调之后，最终设计的到的环量分布与目标吻合良好，平均相对误差为0.058 7，物面升力系数和俯仰力矩系数与目标翼型一致。

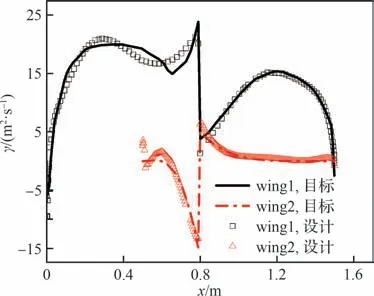
图13 CFD 修正设计后的环量分布Fig.13 Circulation distributions after CFD correction

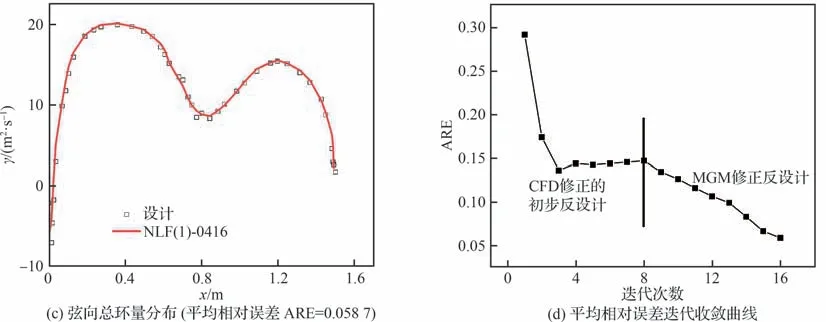
图14 最终设计结果Fig.14 Final design results

3 不同动力翼外形参数分析

在验证了反设计方法的有效性之后，针对动力翼的两个主要设计参数（上涵道壁的弦长Cduct=x2-x1和前后位置x2）对反设计结果的影响进行分析；同时也与给定总环量分布时所参考的目标翼型进行对比，以研究动力翼相比传统翼型的区别和优势。除所分析的参数外，来流和其余动力翼参数取值与第2 节一致。

3.1 涵道壁位置影响

计算分析了涵道壁后缘位置x2=1.5，1.3，1.1 时，不同动力翼反设计结果的升力、阻力和俯仰力矩随迎角变化的情况及与目标翼型NLF（1）-0416 的对比。各翼面目标环量分布如图15所示，反设计结果如图16 所示（图中俯仰力矩参考点取在（0.375，0）处，即1/4 弦长位置）。

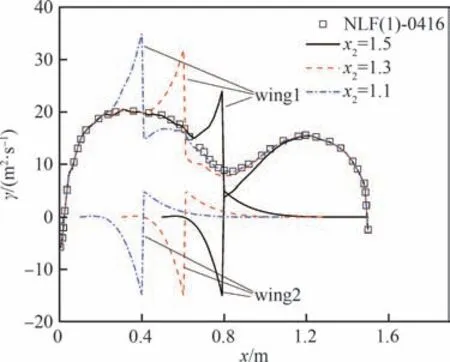
图15 不同x2 反设计目标环量分布Fig.15 Target circulation distributions of inverse design with different x2

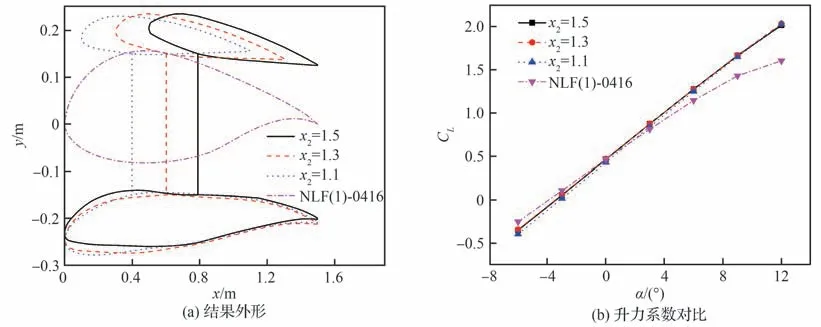
图16 不同x2 反设计结果Fig.16 Inverse design results of different x2

可见在相同的总环量分布下，在0°迎角设计点时，各动力翼方案的升力系数CL和俯仰力矩系数Cm与目标翼型基本一致；随着上部涵道壁前移，其安装角逐渐减小，下翼头部也随之下偏；相比翼型NLF（1）-0416，各动力翼方案的升力系数随迎角变化的斜率CLα基本一致且均偏高，较大迎角时的抗分离能力提升；各动力翼方案物面阻力系数CD（动力翼剖面外形的壁面阻力之和，不包括桨盘推力）均小于目标翼型，涵道壁靠前时物面阻力较小；随着上部涵道壁前移，俯仰力矩系数随迎角变化的斜率Cmα由负到正。

为研究图15 中变化的原因，给出各动力翼方案在0°和12°迎角时的表面压强分布、12°迎角时的流场速度分布以及6°迎角时的弦向总环量分布，如图17～图20 所示。

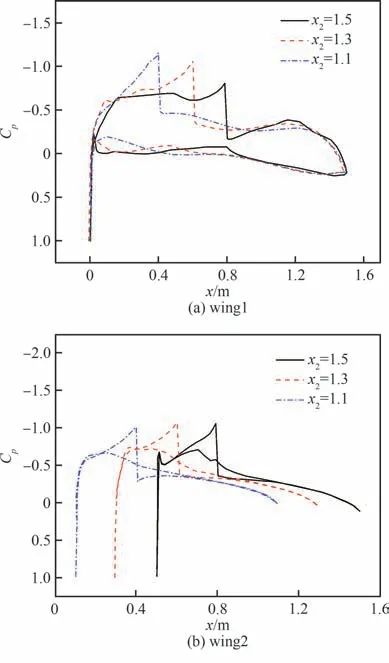
图17 不同x2时0°迎角表面压强分布Fig.17 Surface pressure distributions at α=0° with different x2

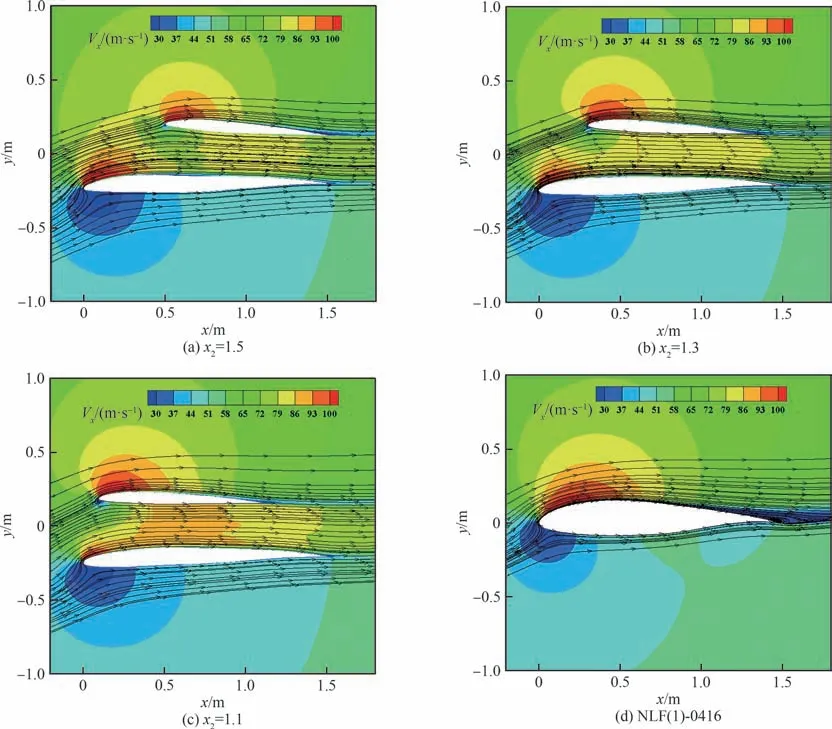
图18 不同x2时12°迎角流场速度分布Fig.18 Velocity distributions of flow fields at α=12° with different x2

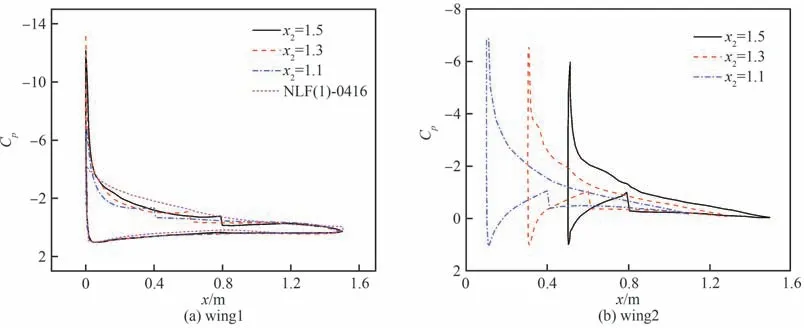
图19 不同x2时12°迎角表面压强分布Fig.19 Surface pressure distributions at α=12° with different x2

图20 不同x2时6°迎角环量分布Fig.20 Circulation distributions at α=6° with different x2

从环量分布看，下翼面环量为正值，其对远场来流有顺时针诱导偏折的效应，当上涵道壁越靠前缘，当地来流迎角相对越大，而其在设计点的目标环量（升力）分布形式不变，因而其安装角越小。从压力分布看，桨盘对入流有抽吸加速的效果，当桨盘位置跟随上涵道壁前移，其对下翼前部附近的抽吸增升也会增加，但下翼前部的目标环量分布不变，所以其前部会对应下偏以抵消升力增量；在12°迎角时，目标翼型的流动分离出现在上表面后缘，而对于动力翼，其下翼后缘处在喷流影响中，上涵道壁的后缘曲率也相对较小，所以动力翼大迎角抗分离能力相对目标翼型有所提高；动力翼阻力系数的下降也是由于桨盘抽吸提高了动力翼尤其是下翼的前缘吸力，因而上涵道壁及桨盘越靠前时阻力越小。从6°迎角环量分布看，随着迎角高于0°设计点，动力翼两个翼面都有显著的前缘吸力峰，且强度大于目标翼型，因而CLα增加；随着上部涵道壁的前移，其环量（升力）增量的作用位置也前移，使得动力翼整体焦点前移，引起Cmα由负到正的转变。

3.2 涵道壁弦长影响

计算分析了涵道壁弦长Cduct=1.4，1.0，0.6时，不同动力翼反设计结果的升力、阻力和俯仰力矩随迎角变化的情况及与目标翼型NLF（1）-0416的对比。反设计目标环量分布如图21 所示，结果曲线如图22 所示。可见在相同总环量目标弦向分布下，在0°迎角设计点时，各动力翼方案的升力系数CL和俯仰力矩系数Cm与目标翼型基本一致；随着上部涵道壁弦长增加，其安装角下降，并且因为相对厚度参数不变，其整体厚度增加；相比翼型NLF（1）-0416，各动力翼方案的升力系数随迎角变化斜率CLα仍然均偏高，其中Cduct=1.4 时 最高；中小迎角时，各动力翼方案物面阻力系数CD仍均小于目标翼型，涵道壁弦长较长时，其厚度增加，但物面阻力仍相对较小；随着上部涵道壁弦长增加，俯仰力矩系数曲线斜率Cmα整体仍由负到正变化。

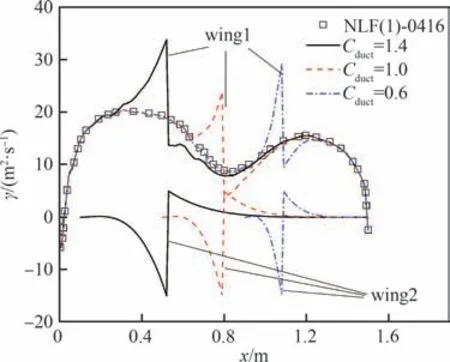
图21 不同Cduct 反设计目标环量分布Fig.21 Target circulation distributions of inverse design with different Cduct

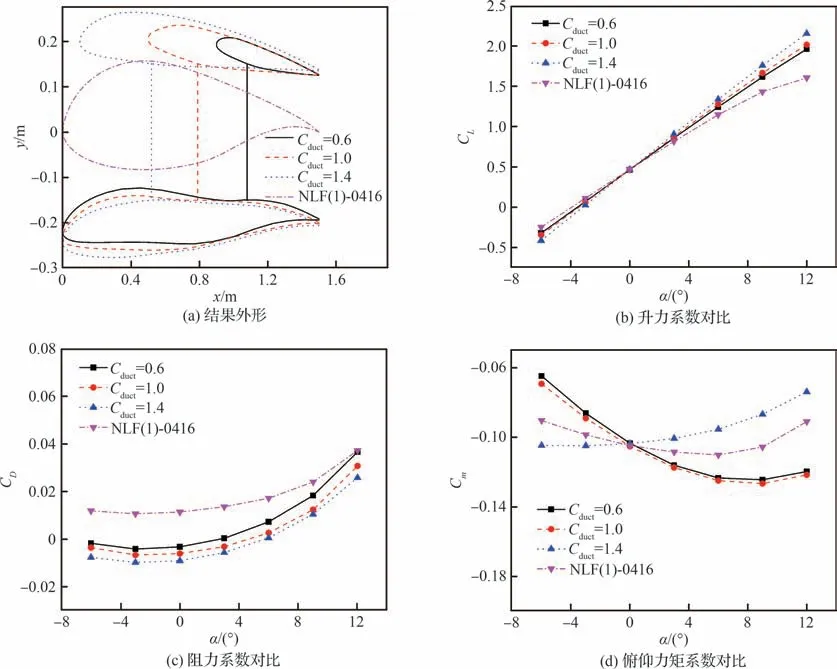
图22 不同Cduct 反设计结果Fig.22 Inversed design results of different Cduct

为研究图22 中现象出现的原因，同样给出不同动力翼方案在0°和12°迎角时的表面压力分布、12°迎角时的流场速度分布及6°迎角时的总环量弦向分布，如图23～图26 所示。

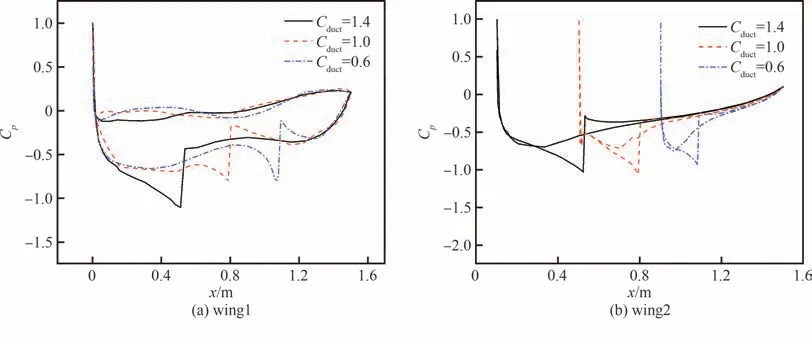
图23 不同Cduct时0°迎角表面压强分布Fig.23 Surface pressure distributions at α=0° with different Cduct

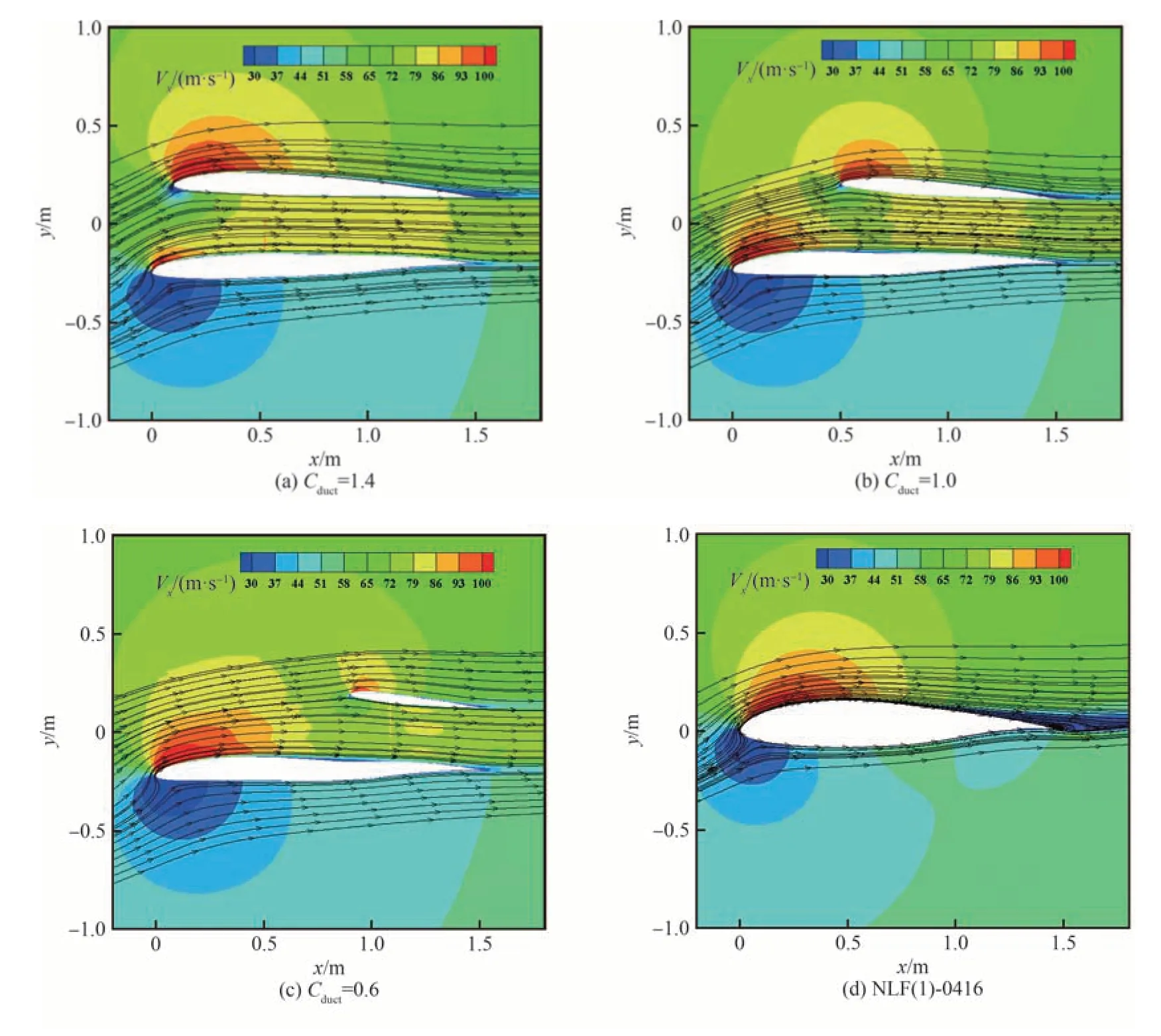
图24 不同Cduct时12°迎角流场速度分布Fig.24 Velocity distributions of flow fields at α=12° with different Cduct

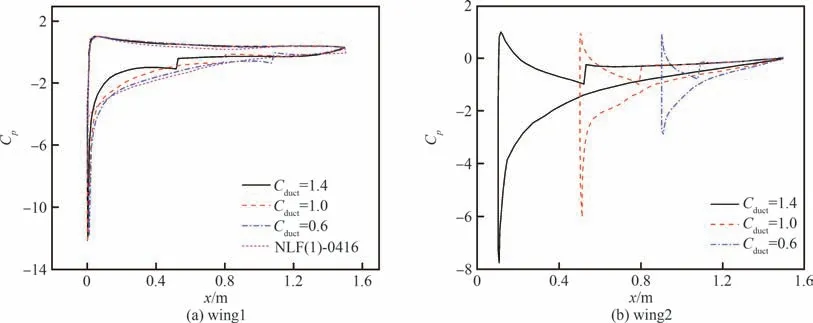
图25 不同Cduct时12°迎角表面压强分布Fig.25 Surface pressure distributions at α=12° with different Cduct

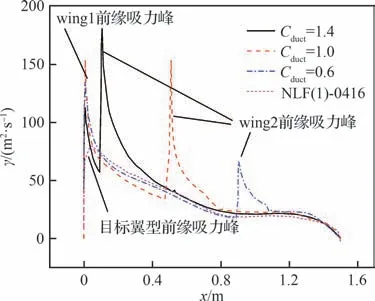
图26 不同Cduct时6°迎角环量分布Fig.26 Circulation distributions at α=6° with different Cduct

从目标环量分布、流场与压力分布看，上涵道壁安装角变化和下翼头部下偏原因与3.1 节分析类似。此外在较大迎角时，目标翼型的流动分离出现在上表面后缘，而对于动力翼来说，其下翼后缘处在喷流影响中，上涵道壁则是在靠近后部且弦长较短时受下翼影响其局部迎角较小，弦长较长时前缘半径较大且安装角较小，所以动力翼大迎角抗分离能力相对目标翼型均有所提高；动力翼阻力系数的下降也是由于桨盘抽吸提高了动力翼尤其是下翼前缘吸力并且强于翼面变厚增加的形阻。从6°迎角环量分布看，随着迎角高于0°设计点，动力翼两个翼面都有显著的前缘吸力峰，且强度大于目标翼型，因而CLα增加；随着上部涵道壁弦长增加，因其翼面尺度变大，其前缘的吸力峰强度和范围显著提高，使得动力翼整体升力系数曲线斜率变大；另外其Cmα由负到正的转变原因也与3.1 节类似。

综合3.2 节和3.1 节反设计所得到的外形来看，其下翼形状有时会出现中部的凹陷，与常规翼型有所区别。这是因为进行的是分布涵道机翼的剖面二维外形的反设计，为满足所给特定的目标环量分布，有时会出现这种外形结果；并且对于这种涵道风扇与翼面耦合的构型，相当于涵道进口附近的下表面较低，这种情况是正常的；根据后续多迎角的分析，其也基本没有产生流动分离等不良影响。实际设计过程中，可从多学科的角度对设计结果进行分析取舍，并对应调整和限制目标环量分布的形式、涵道壁相对位置和长度等参数，使最终的剖面形状符合气动、结构等各学科的期望。

4 动力翼优化设计

在验证了反设计方法的有效性及对两个涵道壁参数的影响进行对比分析之后，继续开展固定总弦向环量分布下的动力翼二维优化设计，以期实现具有最小物面阻力系数（即除桨盘外其他部件的阻力之和）CD的设计结果；此外，考虑到实际转子桨盘应工作在尽可能均匀的来流条件下以降低畸变带来的功率损失及涵道进气段应使总压损失尽可能小，所以在二维优化设计的过程中，使桨盘前20 mm 处的总压恢复系数σ和速度均匀指数U最小，也同样作为优化目标之一。

总压恢复系数σ和速度均匀指数U定义为［1，25］

式中：为来流总压；为各网格处的总压；Ai为各网格面积，二维情况下以截面上的网格高度表征；qi为流量函数。

式中：Vi为各网格上的速度大小；为桨盘处平均速度大小。

优化案例同样以第2 节中的弦向总环量分布为优化过程中每个方案的反设计目标，以第2节的动力翼形状为优化基准，同时固定相同的来流状态和桨盘推力；优化过程中的变量为涵道壁后缘弦向位置x2以及翼型厚度分布参数，其他参数固定为第2 节中的值。翼型厚度分布Z(x)通过6 阶CST 方法进行参数化：

式中：dz为后缘厚度，厚度分布涉及a0～a6共7 个控制变量。优化工作的数学表达式为

3个优化目标的权值比例为0.50∶0.25∶0.25。

优化流程如图27 所示：首先使用最优拉丁超立方方法生成100 个初始样本点，建立Kriging 代理模型以加快迭代速度；然后使用多岛遗传算法进行寻优，使用寻优结果变量进行反设计校核，并更新代理模型数据库，以此循环；最终得到全局优化设计结果。优化算法主要参数设置为：①亚种群规模为20；②岛数为10；③进化代数为10；④交叉、变异和迁移概率分别为1.0、0.01、0.01；⑤ 迁移间隔为5。

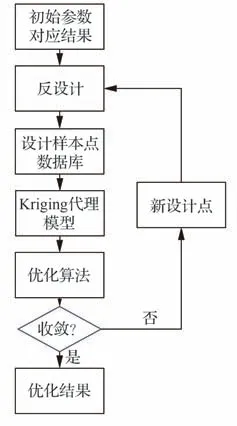
图27 优化框架Fig.27 Optimization framework

图28 显示了初始方案与优化之后的方案对比。相比初始方案，优化后的动力翼剖面形状在设计点升力和力矩特性不变的前提下，物面厚度有所增加，上涵道壁前移，物面阻力系数下降了160%；同时桨盘前入流的总压损失很小，总压恢复系数基本维持不变；此外速度分布的均匀性进一步提升。阻力进一步下降的主要原因与第3 节分析类似，图29 为动力翼表面压力分布对比，可见上涵道壁带动桨盘位置前移，增强了对动力翼前部壁面的抽吸，优化后的上涵道壁前部整体的压力水平较低，进一步降低了前后压差阻力。而通过调整厚度分布，使桨盘入流的均匀性和总压恢复得到了保持，较厚的动力翼剖面形状也有利于结构布置。

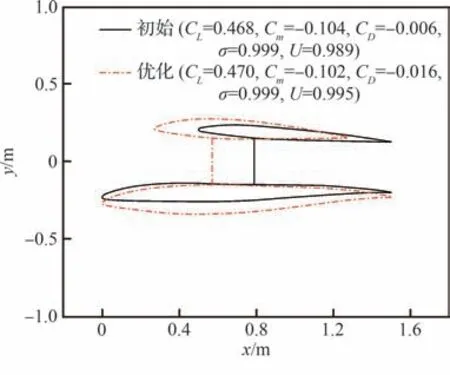
图28 优化结果Fig.28 Optimization results

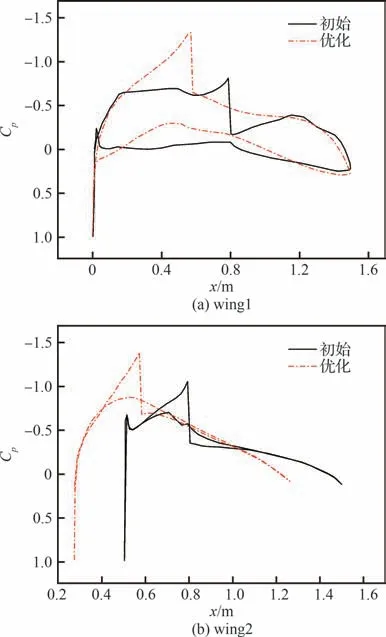
图29 优化结果Cp分布Fig.29 Cp distributions of optimization results

5 结论

基于一种以弦向环量分布为目标的动力翼二维反设计方法，对升力和俯仰力矩相同的动力翼反设计方案进行了涵道壁参数影响分析和进一步的减阻优化设计，主要有以下结论：

1）所使用的动力翼二维反设计方法通过基于翼型理论推导的初步反设计、CFD 修正和MGM 修正方法，能够快速收敛到目标环量分布附近，平均相对误差为0.058 7。

2）随着动力翼上涵道壁位置前移，上涵道壁安装角降低，桨盘跟随前移并对下翼前部的抽吸影响增加，使物面阻力下降、下翼前部跟随下偏；此外动力翼焦点前移，Cmα由负到正变化；迎角大于0°设计点时，动力翼前缘吸力峰比目标翼型更高，所 以CLα较高，并且在12°迎角时仍未出现分离。

3）随着动力翼上涵道壁弦长增加，上涵道壁安装角降低，同样有桨盘跟随前移使其对下翼前部抽吸影响增加，使下翼前部下偏且桨盘抽吸的影响强于涵道壁厚度增加，使整体阻力下降；另外动力翼焦点前移，Cmα由负到正变化；动力翼相比目标翼型的CLα均较高，上涵道壁弦长较长时其前缘吸力峰强度和范围较大，CLα最高。

4）相比动力翼的初始形状，优化后的动力翼涵道壁前移，厚度有所增加，阻力系数下降了160%，同时桨盘入流总压基本没有损失，速度分布均匀性进一步增加。