基于改进VMD算法的水轮机组空化状态仿真实验

苏涛 卢宇

摘 要：为提高水电站水轮机组空化状态识别准确率，提出一种基于振动信号的水轮机组空化状态识别方法。通过利用差分优化算法获取变分模态分解（VMD）最佳分解层数与惩罚因子参数组合改进VMD算法，并利用改进的VMD算法提取水电站水轮机组峰值、偏度、均方根频率等时频特征，然后将提取的时频特征输入BP神经网络中进行分类识别，实现了水电站水轮机组空化状态识别。仿真结果表明，所提方法实现了不同工况下水轮机组水轮和尾水管严重空化、空化加速、空化初生、无空化4种状态的识别，平均识别准确率达到98.88%。相较于基于SVM模型的识别方法，所提方法识别准确率提高了8.76%。

关键词：水轮机组；状态识别；VMD；差分优化算法；BP神经网络

中图分类号：TM769

文献标志码：A文章编号：1001-5922（2024）03-0149-04

Simulation experiment on cavitation state of hydraulic turbine units based on improved VMD algorithm

SU Tao，LU Yu

（Xiangbiling Hydropower Station of Guizhou Jinyuan Weining Energy Co.，Ltd.，State Power Investment Group，Bijie 553107，Guizhou China）

Abstract：To improve the accuracy of cavitation state recognition for hydroelectric turbine units，a vibration signal based cavitation state recognition method for hydroelectric turbine units is proposed.By using the differential optimization algorithm，the optimal combination of the number of decomposition layers and penalty factor parameters of Variational Mode Decomposition （VMD） was obtained，the VMD algorithm was improved，and the improved VMD algorithm was used to extract the time-frequency features such as peak，skewness and root mean square frequency of the hydropower station turbine unit，and then the extracted time-frequency features were input into the BP neural network for classification and recognition，so as to realize the cavitation state identification of the hydropower station turbine unit.The simulation results showed that the proposed method had achieved recognition of four states of severe cavitation，accelerated cavitation，initial cavitation，and no cavitation in the water turbine and tailpipe under different operating conditions，with an average recognition accuracy of 98.88%.Compared to the recognition method based on SVM model，the proposed method had improved the recognition accuracy by 8.76%.

Key words：water turbine unit;state identification;VMD;differential optimization algorithm;BP neural network

水电站水轮机组作为水力发电的重要设备，其安全稳定性直接关系到水力发电效率。然而对于水轮机组而言，由于受到水流流体流态的影响，可能导致水轮机组处于非设计工况（空化状态）中运行，进而降低水轮机组效率，缩短水轮机组使用年限。因此，有必要对水轮机组空化状态进行预防。近年来，刘忠等通过采用傅里叶分解算法分解水轮机空化声发射信号，实现了水轮机空化信号特征提取［1］。汪刚等提出了一种支持向量分类算法（SVCC）用于水轮机空化现象智能识别的分类模型训练，判别准确率达到80%［2］。韩文福等提出了一种基于炮声谱与特殊脉动谱特征提取的水轮机空化智能识别方法，实现了水轮机空化噪声的学习和识别，识别效率达到80%［3］。通过上述研究可以发现，目前针对水电站水轮机组的空化状态识别已向人工智能化方向发展，但普遍存在识别效率有待提高的问題。因此，为解决该问题，提高水电站水轮机组空化状态识别准确性，研究利用变分模态分解VMD算法提取水电站水轮机组空化状态振动信号，应用BP神经网络分类模型进行识别，实现水电站水轮机组空化状态识别。

1 水轮机特征信号提取算法

1.1 ＶＭＤ算法

VMD是一种时频分析方法，通过将输入信号x（t）分解为K个本征模态函数fBi，可将复杂信号分解成多个单分量信号，进而实现特征的提取，如式（1）［4］：

x（t）=∑mi=1 fBi+∑Ki=m+1 fBi+γ（t）  （1）

式中：m为低频有效分量的个数；γ（t）为其余分量。

将模态函数fBi按照频率大小从低到高排列，可得到重构信号y～（t）［5］：

y～（t）=∑mi=1 fBi （2）

1.2 ＶＭＤ算法改进

由于水电站水轮机组原始空化状态信号模态复杂，且具有非线性和非平稳的特点，因此为实现水轮机组空化状态信号特征提取，研究采用VMD算法对该复杂信号进行分解，获取水轮机组空化状态信号特征。但由于VMD算法性能与分解层数和惩罚因子密切相关，而标准VMD算法的分解层数和惩罚因子通常由经验设定，可能存在较大的误差［6-7］。因此，为解决该问题，提高VMD算法性能，研究利用具有较强全局搜索能力的差分优化算法对VMD算法进行了改进。

差分优化算法是一种高效的全局优化算法，具有良好的收敛速度和自适应性［8-9］。

因此，利用差分优化算法获取VMD的最佳分解层数和惩罚因子组合，提高VMD算法性能。基于差分优化算法改进的VMD算法流程如图1所示。

2 水电站水轮机组空化状态识别

2.1 BP神经网络结构

BP神经网络是一种多层前馈神经网络，基本结构如图2所示，包括输入层、隐含层和输出层三部分［10］。其中，X1，X2，…，Xn为网络输入；Y1，…，Yn为网络输出；ωij和ωjk分别表示输入层到隐含层、隐含层到输出层的权值。

BP神经网络具有强大的泛化能力和非线性映射能力，常用于分类识别领域，并取得了良好的成果。因此，研究选用该网络作为水电站水轮机空化状态识别方法。

2.2 水轮机状态识别流程

基于上述改进的VMD算法和BP神经网络，将水电站水轮机组空化状态识别方法设计如下，首先利用改进VMD算法提取水电站水轮机组时频域特征，然后将提取的时频域特征输入BP神经网络中进行识别，即实现了水电机组空化状态识别。

（1）数据收集与整理。收集整理不同工况下水电站水轮机组严重空化、空化加速、空化初生、无空化4种空化状态数据，并进行归一化预处理，然后按一定比例将数据划分为训练集和测试集［11-12］；

（2）改进VMD算法设计。初始化改进VMD算法的分解层数和惩罚因子并计算包络谱信息熵是否满足阈值条件，当包络谱信息熵连续20次低于设定阈值或达到最大迭代次数，输出最佳分解层数和惩罚因子;

（3）特征提取。将输出的最佳分解层数和惩罚因子作为VMD的分解层数和惩罚因子，并利用VMD提取水电站水轮机组空化状态的特征，包括峰值、偏度、裕度因子、整流平均值、均方根值、峭度6种时域特征和均方根频率、重心频率、频率标准差、频率方差、均方频率5种频域特征［13-14］；

（4）BP神经网络模型构建。设置BP神经网络层数为3层，然后根据改进VMD提取的时频域特征，确定BP神经网络输入神经元；根据空化状态类别，设定输出神经元数量;

（5）BP神经网络训练。将训练数据集输入BP神经网络进行训练，并利用交叉熵函数检验模型偏差［15］，当模型偏差满足设定阈值范围时，保存模型，并利用测试集评价模型性能;

（6）状态识别。将待识别水电站水轮机组状态数据通过改进VMD提取特征后，输入训练完成的BP神经网络中，其输出结果即为识别结果。

3 仿真实验

3.1 实验环境搭建

实验基于TensorFlow深度学习框架搭建BP神经网络模型，并在MATLAB软件上进行实现，在Window10操作系统上运行。系统配置Intel 酷睿 i7 8700K CPU，gtx2060 GPU，16 G内存。

3.2 数据来源及预处理

本次实验数据来自自主采集的水电站水轮机组数据，包括3种工况条件下，水电站水轮机组严重空化、空化加速、空化初生、无空化4种空化状态。实验样本数据如表1所示。

最后，对样本数据进行标准化处理，如式（3），并将标准化后的数据按5∶1比例划分为训练集和测试集［16］。

xij=（xij－x-i）/σi（3）

式中：xij表示输入特征i的第j个原始值;x-i、σi分别表示i的均值和标准差。

3.3 评价指标

实验选用准确率（acc）、Kappa系数、F1值作为所提模型识别的性能指标。其中，准确率和F1值的计算方法分别如式（4）和（5）［17-18］：

acc=TP+TNTP+TN+FP+FN（4）

F1=（α2+1）P·Rα2P+R（5）

式中：TP、TN分别表示真正例和真负例；FP、FN分别表示假正例和假负例；P表示精确度，可通过式（6）计算［19］；R表示召回率，可通过式（7）计算［20］；α=1表示调和因子。

P=TPTP+FP（6）

R=TPTP+FN（7）

3.4 参数设置

实验设置改进VMD算法的差分优化算法种群数量为50，变异算子为0.5，交叉算子为0.12，最大迭代次数为100。利用差分優化算法对VMD算法的分解层数和惩罚因子进行寻优，得到不同分解层数为5，惩罚因子为10时，模态分解效果最好。

设置BP神经网络输入神经元数量为11，对应改进VMD算法提取的11个特征值，输出层神经元为4，对应4种空化状态。

3.5 结果与分析

3.5.1 VMD分解验证

为验证所提改进VMD算法的有效性，实验基于水电站水轮机组信号数据对所提算法进行检验。以水轮机组尾水管压力脉动严重空化为例，图3为改进VMD算法分解得到的各模态时频域分量图。

由图3可知，各模态呈现出一定的周期性且模态波形清晰，可完成模态分离和信号分解。

3.5.2 BP神经网络空化状态识别验证

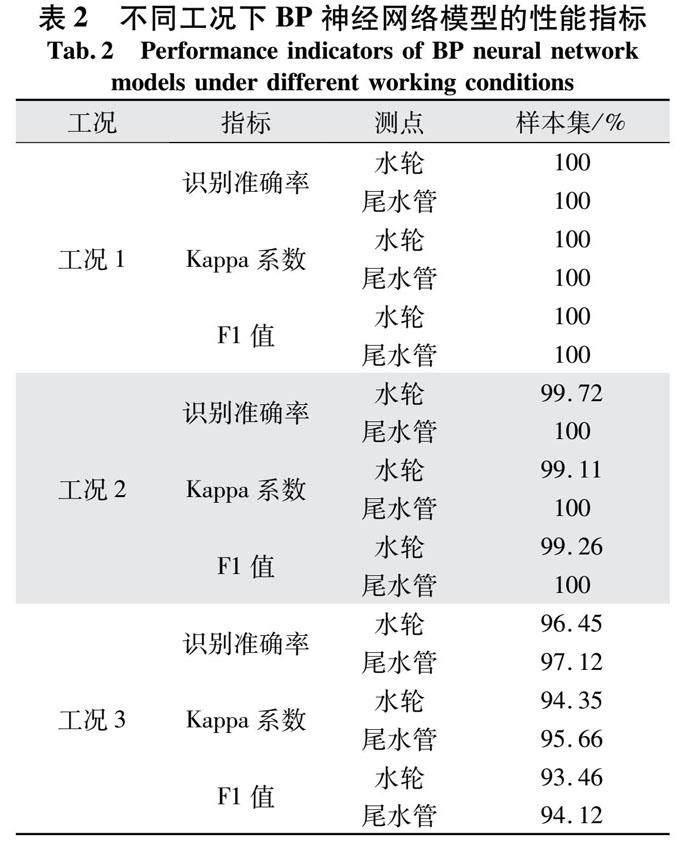
为定量分析所提BP神经网络模型对水电站水轮机组空化状态识别的有效性，实验分析了不同工况下所提模型的各项性能指标，结果如表2所示。

由表2可知，在不同工况下，所提BP神经网络模型对水电站水轮机组的水轮和尾水管均表现出良好的识别效果，各项性能指标均达到95%以上，平均识别准确率达到98.88%。其中，所提模型对工况1条件下水轮机组空化的识别效果最好，各项性能指标达到100%。由此说明，所提的基于BP神经网络模型可有效识别不同工况下的水电站水轮机组空化状态，且具有较高的识别准确率。

为进一步验证所提基于BP神经网络识别模型的有效性和优越性，研究分析了不同工况下所提模型与常用分类识别模型SVM对水电站水轮机组空化状态的识别效果。

工况1，SVM模型对水电站水轮机组转轮、尾水管预测分类与实际分类结果一致，识别准确率率达到100%；工况2，SVM模型预测分类与实际分类结果出现部分误判；工况3，SVM模型预测分类与实际分类结果误判样本增多，识别效果较差。综合来看，基于SVM模型的识别准确率为90.12%，相较于所提的基于BP神经网络模型的识别准确率98.88%，对水电站水轮机组的识别准确率有待提高。由此说明，所提的基于BP神经网络的水电站水轮机组空化状态识别模型具有一定的优越性。

4 结语

综上所述，所提的水电站水轮机组空化状态识别方法，通过利用差分优化算法改进的VMD提取水轮机组空化状态信号时频特征，并将其输入BP神经网络中进行识别，实现了不同工况下水电站水轮机组水轮和尾水管严重空化、空化加速、空化初生、无空化4种状态的识别，且具有较高的识别准确率，平均识别准确率达到98.88%。相较于基于SVM模型的识别方法，所提方法识别准确率提高了8.76%，具有良好的识别性能和优越性。

【参考文献】

［1］

刘忠，李显伟，邹淑云，等.水轮机空化声发射信号降噪与混沌图像特征提取［J］.哈尔滨工程大学学报，2023，44（8）：1361-1367.

［2］ 汪刚，王桂虹，骆彦辰，等.水轮机空化现象智能识别的分类模型训练方法［J］.水力发电，2023，49（7）：67-72.

［3］ 韩文福，倪晋兵，桂中华，等.模型水轮机初生空化的特征谱提取识别方法［J］.水力发电学报，2023，42（8）：69-79.

［4］ 张琰妮，史加荣，李津，等.融合残差与VMD-ELM-LSTM的短期风速预测［J］.太阳能学报，2023，44（9）：340-347.

［5］ 刘可真，普伟，赵庆丽，等.基于VMD–BiLSTM机制的小水电日发电量预测［J］.电力科学与工程，2023，39（9）：28-37.

［6］ 陈天涯，陈盛，郑阳，等.基于VMD-CIMFs-TCN的水电机组振动预测［J］.水电能源科学，2023，41（9）：159-163.

［7］ 郁伟，李正权，邢松.改进WOA-VMD算法的心电信号去噪［J］.中国医学物理学杂志，2023，40（9）：1143-1150.

［8］ 杨韬，李芃，王银花.基于STEKF和VMD-SVD的电能质量扰动信号去噪方法［J］.淮北师范大学学报（自然科学版），2023，44（3）：46-53.

［9］ 張建中，顾冲时，袁冬阳，等.基于优化VMD与GRU的混凝土坝变形预测模型［J］.水利水电科技进展，2023，43（5）：38-44.

［10］ 曹喆，林思地，李正奎，等.基于改进BP神经网络的气流烘丝机控制方法研究［J］.工业控制计算机，2023，36（9）：46-49.

［11］ 任子为，刘彦杰，张仕进.基于BP神经网络的碳钢激光切割工艺参数预测模型及验证［J］.工业控制计算机，2023，36（9）：53-54.

［12］ 周建，陈柯如，闫絮，等.基于BP神经网络的黄土侵蚀沟自动提取方法［J］.时空信息学报，2023，30（2）：193-201.

［13］ 陈国强，申正义，孙利，等.基于BP神经网络优化遗传算法的智能座舱感性意象预测［J］.汽车工程，2023，45（8）：1479-1488.

［14］ 沈恂，刘世军，陈晨，等.基于BP神经网络在线训练的开关磁阻电机无位置控制仿真研究［J］.通化师范学院学报，2023，44（8）：63-67.

［15］ 孟哲，余粟.基于Spark和优化BP神经网络的出租车需求预测模型［J］.数据与计算发展前沿，2023，5（4）：112-126.

［16］ 张谷玉，韩旭.基于BP神经网络-证据理论的产品情感评价策略［J］.包装工程，2023，44（16）：41-47.

［17］ 朱世元，方世鹏.基于深度学习的橡胶制品缺陷检测技术创新［J］.粘接，2023，50（7）：26-29.

［18］ 范德和，李新海，周恒，等.基于卷积神经网络的设备运行状态智能控制优化模型分析［J］.粘接，2023，50（6）：179-182.

［19］ 韩宝辉，赵起超，常荣，等.叶绿素a浓度反演模型：堆栈自编码器粒子群优化BP神经网络［J］.地球信息科学学报，2023，25（9）：1882-1893.

［20］ 徐为海.基于BP神经网络的镇江地区土层剪切波速预测［J］.山西建筑，2023，49（18）：77-80.

收稿日期：2023-10-13；修回日期：2024-01-02

作者简介：苏 涛（1995-），男，助理工程师，主要从事水利电力科学研究；E-mail：lxsut5014@yeah.net。

引文格式：苏 涛，卢 宇.基于改进VMD算法的水轮机组空化状态仿真实验［J］.粘接，2024，51（3）：149-152.