基于广域信息处理的配电网故障隔离技术研究
思 勤,郭 杉,贾俊青
(内蒙古电力科学研究院,内蒙古呼和浩特 010020)
随着电网规模的不断扩大,电网系统逐步朝着智能化、分布化以及精确化的方向发展。而与传统电网相比,现代电网已经具有了故障隔离的功能[1-3]。故障隔离是指通过设备检测与智能算法来定位及预测故障发生的位置,且在故障发生后,系统会进行快速检测,并对故障加以隔离。随着分布式电源(Distributed Generation,DG)[4-6]的大规模接入,电网的建设成本和损耗得到了较大程度的优化,使得组网也更为灵活,可以为用户提供高质量的电力供给服务。
但在接入分布式电源后,电网的整体结构与工作方式较传统电网均存在一定差异。例如分布式电源的接入方式为并联接入,而传统配电网大多为星形结构。同时分布式电源的容量不同,安装位置存在的差异也会对配电网的运行产生一定影响,例如分布式电源电压调节异常、电流过载、电源孤岛等现象均会对故障隔离系统产生较大的影响。因此,文中在包含分布式电源的配电网络中提出了一种电网故障隔离方法,以保证电网的正常和平稳运行。
1 电网故障隔离模型设计
1.1 含DG的配电网故障定位模型
在配电网中加入DG 支路后,其网络拓扑将变得复杂,并会对电路中电流、电压的方向以及功率产生较大的影响。同时,DG 并入配电网中闭合与关闭所产生的振荡和过冲均会对电网的运行造成影响,进而导致对故障的定位更加困难。包含DG 的配电网模型如图1 所示。
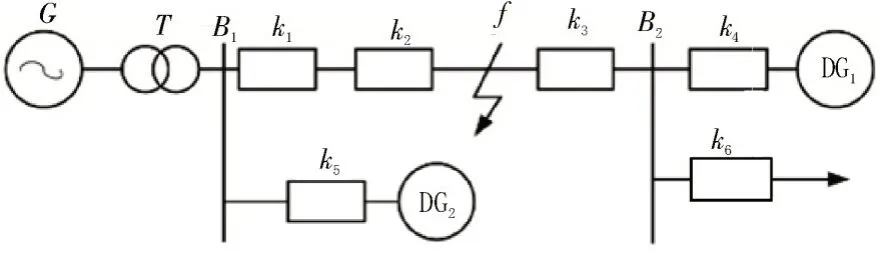
图1 包含DG的配电网模型
图1 中,每个矩形均表示一个馈线终端单元(Feeder Terminal Unit,FTU),电流按照箭头的方向依次经过FTU,f为模拟故障点。假设f点发生短路故障,而DG1、DG2未接入电网中,则k1、k2点均会检测到该故障,此时使用信号分析算法即可判断故障发生在k2和k3之间。当分布式电源DG1、DG2接入电网后,整个电网将会由原来的G点供电变为三点多电源供电,此时电流流向就会发生变化。若f点发生短路故障,DG1供电会使k3也检测到故障电流。传统算法是将DG1、DG2以及G点依次断开,记录故障数据后再进行综合分析,以获得故障发生的位置。但该算法操作复杂,准确度也较低。因此,文中使用改进的经验模态分解(Empirical Mode Decomposition,EMD)算法、粒子群(Particle Swarm Optimization,PSO)算法和支持向量机(Support Vector Machine,SVM)对电路相关信号进行分析,并快速完成故障定位,进而实现故障隔离功能。
1.2 复杂信号分析算法
经验模态分解算法(EMD)[7-9]能在时域和频域中实现对信号的自动分解,即对信号的筛选。经过这一筛选过程,信号被分解为多种本征函数,而每个本征函数均可被看作是包含有不同频率分量的信号。含有DG 的配电网系统具有多个电源,产生的信号为复杂信号,使用EMD 算法便可将其分解。而EMD 算法将信号分解为本征信号需要满足以下条件:
式中,Nz为函数最值点的个数,Ne为函数零点的个数,fmax(ti)为函数的上限包络,fmin(ti)为函数的下限包络。EMD 分解的主要步骤如下。
步骤1:设原信号为x(t),使用三次样条插值法对函数的最大和最小值点进行拟合操作,以获得对应的上下包络线。同时,求出上下包络线的平均值m(t),并计算x(t)与m(t)的差值,再根据式(1)判断是否满足本征函数的筛选条件。若满足,则将该差值记为IMF1;否则,将差值作为新的信号h(t),且按照上述步骤继续筛选新的本征函数。直至本征函数出现,该步骤结束。
步骤2:从复杂信号x(t)中去除IMF1信号并生成新信号,再对新信号按照步骤1 进行计算,从而得到IMF2;继续不断循环,直至获得设定本征函数值IMFn。筛选终止条件为:
其中,ε是判决阈值。由步骤1、2 可以得到n个IMF 本征信号及一个剩余信号项s,即:
EMD 分解的具体流程如图2 所示。
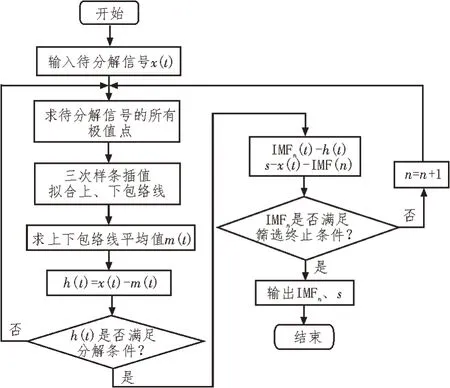
图2 EMD分解流程
1.3 基于树形SVM的故障诊断算法
支持向量机(SVM)[10-12]针对的是线性多分类问题,其基本思想是对多个样本划分最优超平面,具体如图3 所示。

图3 支持向量机基本思想
图3 中,划分最优超平面的直线可表征为:
式中,ω和b为需要求解的参数。因此,可将问题转化为线性规划的求解问题,则有:
该线性规划问题可以通过拉格朗日法[13]进行求解,计算过程如下:
文中配电网故障信号经EMD 算法分解后情况较为复杂,故使用单个SVM 算法通常无法满足要求。因此,使用二叉树SVM 算法进行故障诊断。
分解后的信号分析可以抽象为一个k类的分类问题,算法可表示为四元算法组,即:
式中,q为二叉树的根节点集合,集合个数为问题的分类数量;p为分类数量的权重排序;SVM 为二叉树集合;DC 为样本数量集合。
采用二叉树SVM 算法训练样本的效率较高,故训练时间会缩短。文中根据故障类别使用4 个SVM对故障分析模型进行分析。二叉树模型如图4所示。

图4 二叉树模型
1.4 基于PSO的SVM参数优化算法
SVM 参数可由式(6)计算得到,但算法的效率及计算准确率均较低,因此该文使用粒子群算法[14-16]对参数进行优化,以实现SVM 的自动优化。
粒子群算法(PSO)是一种模拟鸟类捕食的仿生学启发算法。若种群个数为m,维度为n,种群可用x=(x1,x2,…,xm)T表示。设种群中个体最接近食物的位置为pbest,整个种群最接近食物的位置为gbest,且个体接近食物的过程由自适应度fit 控制。每个个体均会不断迭代自身的飞行速度以及实时位置,二者的迭代公式如下:
式中,vid、xid分别为个体某时刻的速度及位置;β为权重值;c1和c2为学习因子;r1、r2为0~1 之间的随机数;pid及pgd分别为粒子个体与种群极值的位置。粒子群算法的执行流程如图5 所示。

图5 粒子群算法执行流程
1.5 EDM-PSO-SVM算法流程
算法流程如图6 所示。数据样本分为训练和测试样本集,二者均可通过EMD 算法进行分解;分解后的数据再输入至SVM 模型中进行训练,同时SVM的模型参数则由PSO 算法加以优化。最终输出故障检测结果,并实现故障隔离。

图6 算法执行流程
2 实验与分析
2.1 实验环境搭建
实验使用IEEE 标准33 节点配电网模型进行算法仿真,该配电网如图7 所示。其中,DG1-DG3为3 个分布式电源,编号1~33 的黑色小节点为开关节点。
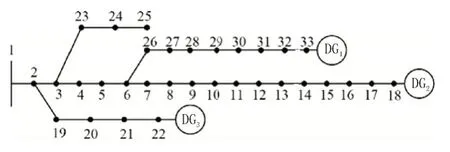
图7 配电网模型
实验所采用的仿真工具为Matlab R2018a,同时根据所提算法来编写对应程序。此外,PSO 种群个数为100 个,算法迭代次数为45 次,数据维度选择30维。实验相关配置如表1 所示。

表1 配置参数
2.2 算法测试
为验证所提算法的可行性,根据编写的程序进行故障隔离实验测试。首先假定电路中有一处故障,且其发生的位置随机,DG1、DG2以及DG3表示分布式电源,0 和1 则表示电源的开启状态。实验测试结果如表2 所示。
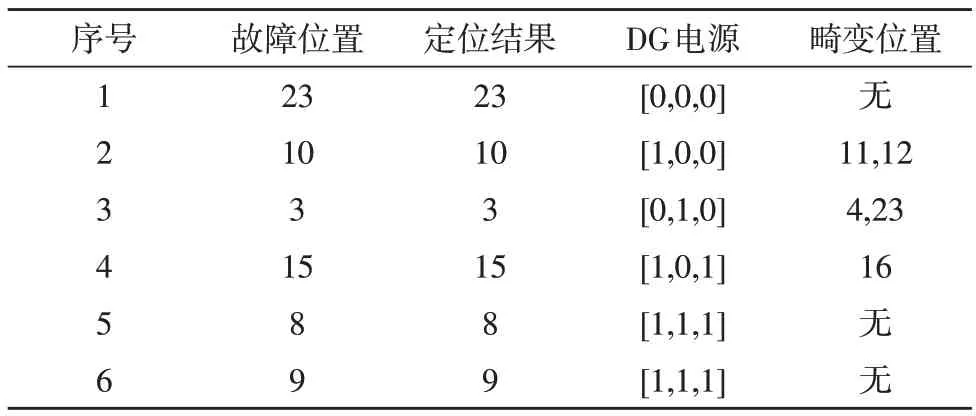
表2 单故障测试结果
由表2 可知,当配电网不包含分布式电源时(序号1),算法可准确地对故障进行定位,这表明该算法能对不含DG 的配电网进行故障定位。而当配电网中包含DG 时,可以看到虽然在部分位置出现了畸变,但该算法也同样能够对故障进行定位。由此证明,该算法对于单故障段定位的可行性。
对配电网而言,多故障是最常发生的现象,因此文中在配电网中随机放置了多处故障来对算法进行检测。实验结果如表3 所示。
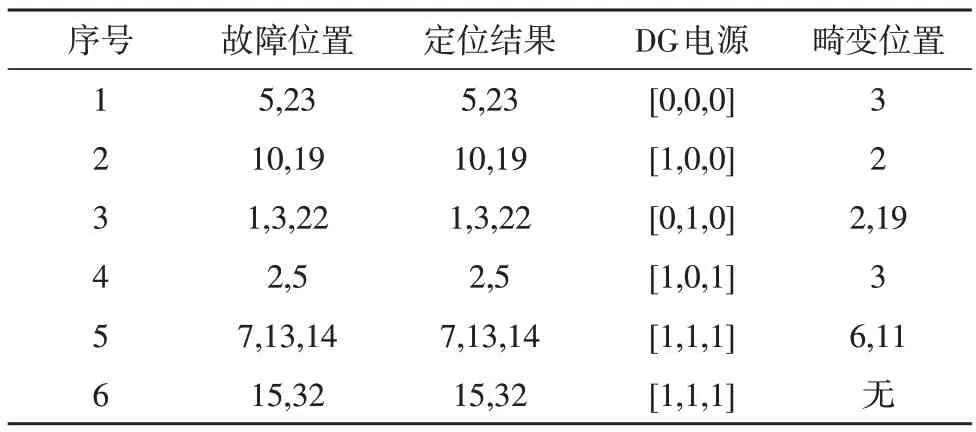
表3 多故障测试结果
从表3 中可以看出,所提算法在多故障检测实验中全部检测正确,且检测项次中并无漏报、错报等现象。尽管畸变现象进一步加重,但该算法能够对配电网中的多故障进行有效检测。
为了对所提算法的性能进行更为客观的评估,在实验中加入GWO-SVM、IWO-SVM 以及SVM 作为对比算法,评估指标为故障成功定位次数以及运行时间,仿真测试共进行30 次,结果如表4 所示。

表4 对比算法测试结果
表4 中,基础SVM 算法的定位成功率最低,而使用GWO、IWO 以及文中PSO 算法对SVM 参数进行优化后,成功率均有一定程度的提升,但该文算法的成功定位次数最多,表明其性能良好。此外,由于采用了EMD 信号分解算法,平均运行时间也最短,说明其效率也较优。
3 结束语
含有DG 的广域信息配电网传输信号通常较为复杂[17-18],且难以对其进行分析。文中针对传统分析方法所存在的不足,提出了一种基于广域信息处理的电网故障隔离技术。该技术使用EMD 算法对信号进行采集分解,并利用SVM 提取信号的特征,再采用PSO 算法优化SVM 参数,进而使模型的训练速度得以提升。实验测试表明,该文算法在所有对比算法中的平均运行时间最低且定位准确率最高,综合性能及效率俱佳,可以应用于实际的电网故障隔离系统中。

