基于灰色BP 神经网络的电力碳排放峰值预测
吴海杰,王联智,谢敏,王康桑,符艺超
(南方电网海南数字电网研究院有限公司,海南海口 570203)
现阶段,我国经济发展过程中面临着许多环境问题,其中最为紧要的问题是发电公司的二氧化碳排放量较高。因此,如何正确地预测碳排放峰值,结合预测结果制定碳减排策略,并在短时间内控制碳排放峰值,这均成为了现代社会发展过程中急需解决的问题。目前,学者们从不同的角度和理论出发,研究碳排放峰值预测方法。文献[1]提出了基于STIRPAT 模型的峰值预测方法,在能源结构优化模式下构建了STIRPAT 模型。该模型结合VSTE 算法计算电力碳排放平均值,进而预测碳排放峰值。然而,该方法过分依赖人工操作,使得构建的模型在求解过程中受到不同因素影响,出现了较大预测误差。文献[2]提出了基于双回归预测模型的峰值预测方法。构建了电力碳排放双回归预测模型,根据电力耗能情况,将不同电力设备运行参数进行了相关处理,并将其输入到预测模型中,实现电力碳排放峰值精准预测。该方法虽然能够快速取得预测结果,但在实际操作过程中无法很好控制碳排放总量,因此预测结果还存在一定的误差。
针对上述方法所以存在的问题,提出了基于灰色BP 神经网络的电力碳排放峰值预测方法。灰色BP 神经网络具有较好的非映射性能,还能够根据实际情况灵活地设定参数,能够降低预测误差,提升预测精度。
1 基于灰色BP 神经网络的预测模型构建
基于误差反传播的灰色BP 神经网络具有连续逼近函数极限值的优势,使得预测结果存在最优解[3]。此外,还可以根据不同环境设定模型结构的层数、单元数及训练因子等,使预测过程更具有灵活性和随机性,提升预测精准度与效率。灰色BP 神经网络能够训练大量数据,并明确数据之间的关系[4-5]。采用快速下降方法通过反向传递不断地调节网络权值和门限,从而减小网络的误差。该方法的核心思想是引入一种新的学习方法,通过对网络逆向传递进行迭代修正和训练,使得网络输出矢量与所需矢量保持一致。
灰色BP 神经网络模型将随机变量视为一定区间内变动的灰色变量,经过处理后累加序列都呈现指数增长趋势[6],该情况下的原始数据序列和累加序列分别为:
将原始数据序列和累加序列作为输入值,构建基于灰色BP 神经网络的碳排放峰值预测模型,如图1 所示。

图1 预测模型
在网络输出层的错误平方和小于规定值时,完成了模型训练,以此能够有效降低网络加权次序偏差[7]。模型训练具体步骤是:通过对各个节点初始化,随机地分配各个节点权重和门限。在参数设定完成的情况下,分别对输入层和输出层连接权重和阈值进行计算。选择下一种输入方式,反复迭代,直到网络输出结果符合规定为止。
2 电力碳排放峰值预测模型求解
为了求解电力碳排放峰值预测模型,在灰色BP神经网络中引入了递推算法,该算法通过选取随机碳排放路径,计算各个因子对应的影响权值,进而获取相应路径碳排放数值[8-9]。随机选取的碳排放新路径为:
式中,Li表示第i种碳排放量路径;λ表示碳排放系数[10];L′(ξ)表示碳排放路径抽取函数[11]。在计算电力碳排放量过程中,使用递推算法计算电力碳排放量,公式为:
式中,ai表示第i种电力消费模式;fi表示第i种电力折标系数;λi表示第i种电力碳排放系数;j表示电力设备数量。
递推算法采用的是随机选择电力碳排放路径方式,主要是通过对不同路径上碳排放影响因素分析,获取最大和最小碳排放周期[12]。具体的操作流程如下:
步骤一:随机获取各路径碳排放量,通过引入微分方程参数,对其进行加权处理,得到了新的灰色BP 神经网络模型。
步骤二:采用正规化的方法剔除了数据之间的非线性关系,并将其引入到模型中。利用Lasso 回归分析方法,分析了各因素对碳排放量峰值预测的影响[13-14]。Lasso 回归分析通过惩罚函数来压缩模型中的系数,将一些因子变成0,以筛选出显著变量。
设a为自变量,b为因变量,经过m次取样后得到的预测样本标准值为(a,b),自变量a的第k个预测值为:
式中,T表示预测周期。因变量对自变量的回归模型可表示为:
式中,εi表示随机自然数。如果要筛选出影响显著变量,需要给该公式添加一个条件,约束表达式为:
式中,t表示调和参数;φ表示最佳调整阈值。Lasso 回归就是通过不断调整调和参数值,降低回归系数,压缩变量系数直到为0,以此获取显著变量,即碳排放峰值[15]。
步骤三:由于电力碳排放量计算具有邻接性,因此在计算一个节点的碳排放量时,仅需获得邻近节点碳排放量,无需了解该节点碳排放流信息,碳排放流邻接特性示意图,如图2 所示。

图2 碳排放流邻接特性示意图
通过对各节点功率分配,可以得出各节点间的联系。根据电网碳排放邻接性,依次求取初始点到不同节点的碳势。在每次递推时,在确定某一节点碳势后,就可求取全部节点碳势。因此,每一次递推都能在任意一段时间内获取精准的节点碳势计算结果。最终,利用有限递推方法,求出了网络中全部节点碳势[16]。具体计算公式如下:
式中,Pi表示节点注入的有功功率;Gj表示电力机组支路有功功率;Ωi、Ωj分别表示第i、j两个电力碳排放及节点注入的集合。判断是否所有节点都已经轮询完毕,若是获取了全部节点碳势,完成递推。
步骤四:在偏差允许的条件下,实现了预测模型的求解,得到了电力碳排放量峰值预测结果。
3 实验
为了验证研究的基于灰色BP 神经网络的电力碳排放峰值预测方法是否合理,设计了相关实验,以此来验证方法的可行性。
3.1 实验过程
分析了电力碳排放流,其示意图如图3 所示。
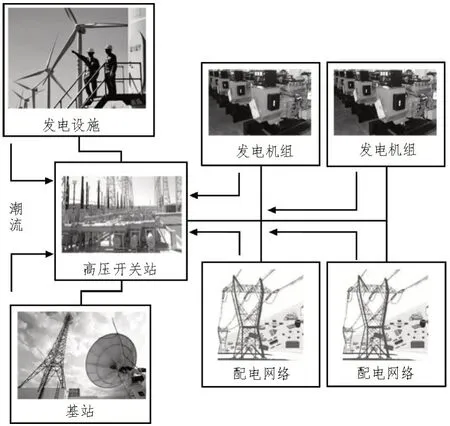
图3 电力碳排放流示意图
通过分析配电网络与主网功率交换方向及规模,确定各主要网络间的碳排放量的计算次序。若将有功电力注入到主网,则可将其作为主网供电,而不能作为主网负荷。若将有功电力注入到主网配电网络中,利用分布式电源与常规火电厂之间边界信息,对配电网络中碳排放进行分析。在此基础上,将根节点的碳势和注入功率作为主网的重要变量,对主要网络碳排放量进行了计算。根据主网碳排放流量分析了其碳排放流的分布。
3.2 实验数据分析
碳排放峰值不是表示一年碳排放量达到峰值,而是从这一年开始某个地区碳排放量出现稳定趋势。在基准情景、低碳情景和强化低碳情景下,采集碳排放峰值如表1 所示。
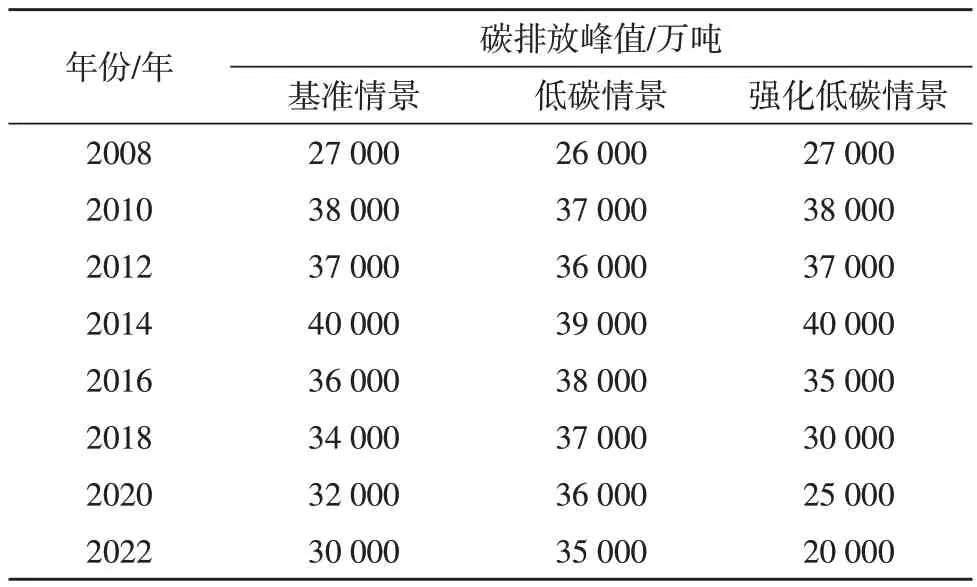
表1 碳排放峰值采集结果
由表1 可知,基准情景、低碳情景和强化低碳情景下碳排放峰值分别为40 000 万吨、39 000 万吨、40 000 万吨,在2014-2022 年三种情景的碳排放均呈缓慢下降趋势。
3.3 实验结果与分析
检验文献[1]方法、文献[2]方法和研究方法的电力碳排放峰值预测结果,如图4 所示。

图4 三种方法峰值预测结果
由图4(a)可知,在基准情景下文献[1]方法碳排放峰值与表1 数据存在最大为600 万吨的误差;在低碳情景下文献[1]方法碳排放峰值与表1 数据存在最大为500 万吨的误差;在强化低碳情景下文献[1]方法碳排放峰值与表1 数据存在最大为400 万吨的误差。由图4(b)可知,在基准情景下文献[2]方法的碳排放峰值与表1 数据存在最大为400 万吨的误差;在低碳情景下文献[2]方法的碳排放峰值与表1 数据存在最大为500 万吨的误差;在强化低碳情景下文献[2]方法的碳排放峰值与表1 数据存在最大为600万吨的误差。由图4(c)可知,使用所研究方法在三种情景下的碳排放峰值与表1 数据一致。
通过上述分析结果可知,使用所研究方法电力碳排放峰值与实际数据一致,说明该方法的预测结果更为精准。
4 结束语
由于碳排放变化趋势呈现非线性,灰色BP 神经网络进行碳排放峰值预测,原因在于灰色BP 神经网络具有较好非映射性能,还能够根据实际情况灵活地设定参数,使用Lasso 回归筛选法和递推算法对该模型进行了求解,得到了相关的电力碳排放峰值预测结果。实验结果表明,在基准情景、低碳情景和强化低碳情景下,所研究方法的碳排量峰值与实际数值一致,都为40 000 万吨、39 000 万吨、40 000 万吨,由实验验证了所研究方法的合理性,能够为碳排放控制提供技术支持。
——《2013年中国机动车污染防治年报》(第Ⅱ部分)

