基于DQN 算法的泵站供水系统节能控制优化
陈财会,张 天,黄健康,金 典,王卓悦,张小磊
(哈尔滨工业大学<深圳>土木与环境工程学院,深圳 518055)
随着我国城镇化的不断深入推进,我国城区人 口由1981 年的1.4 亿人增长至如今的4.4 亿人。为保障城区人口的用水需求,我国给水事业发展迅速,城镇供水系统投资规模日益扩大。 据国家统计年鉴数据,2021 年年底全国供水总量达到631 亿m3,供水投资为771 亿元[1]。 我国供水企业每年需要投入大量的能源成本,以维持庞大供水体系,其中高达95%的电耗用于维持水泵的运转[2]。 故而,泵组的优化调节已被证明是降低整个供水系统运行成本的切实有效的方法[3]。
《中华人民共和国国民经济和社会发展第十四个五年规划和2035 年远景目标纲要》(简称“十四五”规划)明确指出,要加快交通、能源、市政等传统设施数字化改造,全面提高资源利用效率,强化重点用能单位节能管理,实施能量系统优化、节能技术改造等重点工程[4]。 根据“十四五”规划的指导,研究出现实可行的系统优化算法是解决供水系统能量浪费问题的重要方向之一。
在我国城市供水体系中,由于泵站大多采用人工调节的方式,其往往根据历史经验制定各水泵运行转速和启停方案,虽然可满足当前用户端的用水需求,但未考虑供水泵站总体运行效率,存在运行效率低下、能量浪费问题[5]。 因此,在满足城镇居民用水需求的前提下,提升供水泵站中泵组总体效率所带来的节能效益十分可观。
泵站中水泵组运行状态的节能优化问题,可抽象为在供水需求不断变化的情况下,以水泵组总效率为优化目标,水泵高效区为约束条件的动态规划问题。 而深度强化学习算法既具有良好的感知能力,又具有良好的决策能力。 目前,已有许多研究[6]证明,深度强化学习算法在动态规划问题上具有良好的适用性,且已被广泛应用于工业制造、优化调度、游戏博弈等领域。 而深度强化学习在我国供水领域中应用很少,具有良好的研究前景。 Zhang等[7]首次提出将粒子群优化算法应用于水厂中进水泵组的优化运行,最终实现节电4.2%的效果。
目前,成熟的深度强化学习算法包括Qlearning、深 度Q 网 络(deep Q-learning network,DQN)、深度确定性策略梯度(deep deterministic policy gradient,DDPG)等算法[8-9]。 由于水泵的流量和扬程在数值上连续变化,本文针对水泵组运行状态的节能优化问题,采用适应于连续状态空间的DQN 算法进行泵站供水系统最优节能控制研究。
1 理论设计计算
1.1 优化水泵组运行状态问题的数学描述
1.1.1 水泵高效区的界定
在求解水泵组运行状态优化问题之前,应先定义何为水泵的高效运行,即界定水泵的高效运行区。变频泵的高效区如图1 所示,在额定转速下,水泵运行时的效率η是关于流量Q的非线性函数,其峰值为水泵运行的最高效率。 通常取最高效率的90%为高效段的下限,此时对应的流量分别图1 中的QA、QB,其工况点为水泵高效运行区的边界点,即图1 中的A、B 两点,对应的扬程分别为HA、HB。
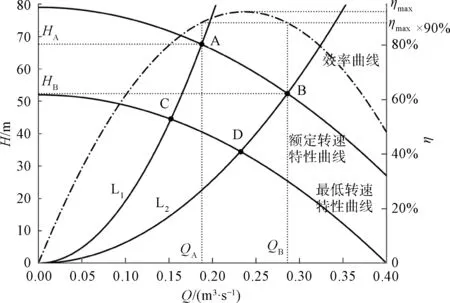
图1 变频泵的高效区Fig.1 High-Efficiency Area of Variable Frequency Pumps
设额定转速下,水泵的特性曲线方程如式(1)。
其中:Hx——虚总扬程,m;
Sx——泵体内虚阻耗系数;
H——扬程,m;
Q——流量,m3/s。
当调节水泵转速n时,图1 中水泵的特性曲线也会改变。 现计算任意转速ni下水泵的特性曲线方程。 由水泵的相似定律可得式(2)~式(3)。
其中:Q0、Qi——额定转速n0和任意转速ni下的流量,m3/s;
H0、Hi——额定转速n0和任意转速ni下的扬程,m;
ki——调速比。
将式(2)和式(3)代入式(1)得到式(4),即为任意转速下水泵的特性曲线方程。
为防止水泵因超载运行而损坏,水泵转速不宜超过额定转速n0。 此外,为防止气蚀现象的产生,水泵的转速不能过低,因此,需设立最小转速nmin,相应的最小调速比为kmin。 则最小转速下的水泵特性曲线方程为式(5)。
此时水泵的高效区拓展至图1 中的环扇形区域ABDC,其由4 条曲线围成,分别为额定转速和最低转速下的水泵特性曲线,以及由A、B 两点引出的相似抛物线L1、L2。 在同一条相似抛物线上,各点所对应的水泵效率相等,所以相似抛物线L1、L2上的点同样为对应转速下的高效段边界点。 相似抛物线L1、L2的方程分别为式(6)~式(7)。
通过联立式(5)~式(7),可解出C、D 两点分别对应的扬程HC、HD和流量QC、QD。 再根据A、B、D、C 分别对应的Q值和H值,即可得到高效工作区。
1.1.2 目标函数建立
本文对优化泵组运行状态问题的数学描述如下:设泵组中含有x台变频泵,y台工频泵,各泵的泵型确定,管路特性曲线确定,且采用并联供水方式。 已知供水流量要求Qsum和扬程要求He,求得水泵的运行组合以及各水泵的调速比ki,在泵站达到供水要求并且各个水泵均处于高效运行状态的前提下,使泵站达到最高总效率。
基于该问题描述,泵站供水时,系统优化的目标函数如式(8)。
其中:γ——水的容重,N/m3;
Qsum——供水总流量要求,m3/s;
He——供水扬程要求,m;
η——效率;
Ni——第i台泵的功率,W。
1.1.3 设置约束条件
水泵的工况点必须在其高效区内,以此为约束条件,数学描述如式(9)~式(10)。
其中:Qmin、Qmax——高效区限制,如式(11)~式(12)。
1.2 优化泵组运行状态问题的马尔可夫决策过程描述
本文采用的DQN 算法是强化学习的经典算法之一,用于解决智能体(agent)与环境(environment)的交互中,寻求最佳策略并获得最大利益的问题。
而马尔可夫决策过程(Markov decision process)为强化学习算法提供框架[10],其模型可用元组(S,A,T,R,β)表示。 其中,S表示系统的状态空间;A表示动作空间;T代表状态转移矩阵,即从某一状态执行特定动作后转变为另一状态的概率;R为执行特定动作后获得的即时奖励;β为折扣系数(β∈[0,1]),即未来奖励的重要程度,可以避免马尔可夫决策过程陷入无限循环。
在供水系统中,供水流量要求Qsum和扬程要求He是随机量,故优化水泵组运行状态问题可视为不确定条件下的贯序决策问题,适用于马尔可夫决策过程模型。 本节将该问题表述为马尔可夫决策过程,并对模型参数进行定义。
1.2.1 状态空间
在某一时间步(step)中,智能体将观测环境的状态,该状态包括各个水泵的运行状态,包括流量、扬程等参数,其表达式如式(13)。 由于泵站供水的方式普遍采用并联式供水,各个水泵的扬程视为相同。
1.2.2 动作空间
当智能体获取环境状态S后会给出动作A,其包括调控各变频泵的转速以及各工频泵的启闭状态。 本文将对变频泵和工频泵的调控分别划分为动作空间Av和Ag,表达式如式(14)~式(15)。
其中:Av——智能体对变频泵的调控,0 为调低转速,1 为转速保持不变,2 为调高转速;
Ag——智能体对工频泵的开闭状态,0 为开启,1 为关闭;
a∈A,i∈[1,x],j∈[1,y]。
1.2.3 状态转移函数
传统的马尔可夫模型通过状态转移矩阵预测未来的状态,但当状态空间为高维连续时,可采用状态转移函数进行预测,即式(17)。
状态转移函数可通过神经网络学习而得。
1.2.4 即时奖励
智能体在状态s时执行动作a,会获得即时奖励r。 因为优化水泵组运行状态问题的目标为最大化泵站总效率,设电机效率不变,则即时奖励r可设置为式(18)。
2 设计方案
2.1 DQN 算法流程
DQN 算法是在马尔可夫决策过程提供的框架下求解强化学习问题的算法之一,需满足马尔可夫决策过程的假设条件[11]。 因此,可在上述马尔可夫决策过程描述的基础上,构建DQN 算法流程,其总体过程为智能体基于环境反馈的奖励,学习出每个状态下的最优动作。
对于当前状态最优动作的判断,需要动作价值函数Q(s,a)提供该状态下每个动作的价值。 而估值网络Q负责输出当前状态下所有动作的价值函数{Q(s,ai)|i= 1,2,…}。 因此,动作价值函数的准确与否,决定智能体的决策是否合理。 为不断修正动作价值函数,DQN 算法引入目标网络Qtarget 和经验回放池replay_memory,以不断更新估值网络的权重。经过多轮更新,智能体能够判断出每个状态下的最优行为,但为防止陷入局部最优,智能体在选择动作时,会采取ε-greedy 策略,即有小概率选择随机动作,而不根据动作价值函数Q(s,a) 进行选择。
DQN 算法原理如图2 所示,概念说明如表1 所示。

表1 DQN 算法中相关概念说明Tab.1 Instruction of Related Concepts in DQN Algorithm
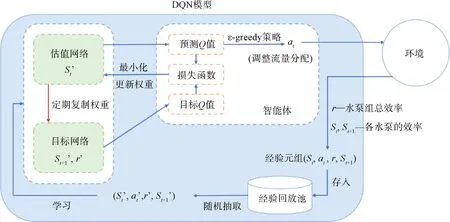
图2 DQN 算法原理Fig.2 Principle of DQN Algorithm
基于DQN 算法,水泵组运行状态调控的训练过 程如图3 所示。
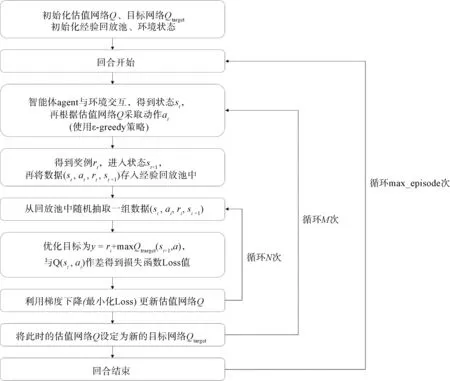
图3 DQN 算法过程Fig.3 Process of DQN Algorithm
2.2 仿真环境的搭建
2.2.1 设置供水场景
本文以深圳M 给水厂及其负责片区的供水情况为训练场景。
总流量与扬程数据源于给水厂提供的周供水数据,其中前5 d 的数据用于训练,后2 d 的数据用于结果评估。 供水所用的泵组中,设置5 台变频泵,采用并联供水方式,其具体参数如表2 所示。

表2 水泵性能参数Tab.2 Parameters of Pump Performance
2.2.2 供水过程中各个水泵的功率N 和效率η的确定
评估DQN 算法优劣性的基础是仿真环境能否准确模拟供水需求和水泵组运行状态。 若模拟变频泵的工作状态,则需要得到在任意转速下变频泵的功率N关于流量Q和扬程H的定量关系式。 对于已投入运营的大型水泵,通过现场测试该关系式较为困难,而通过分析水泵的性能曲线图得到该关系式则较为容易。
水泵性能曲线如图4 所示。
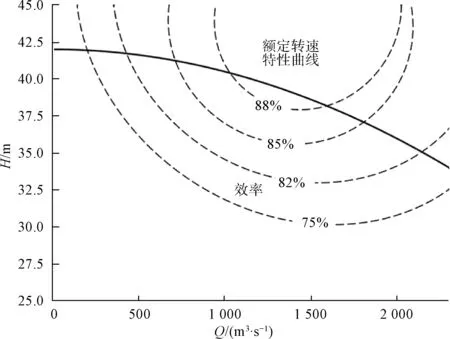
图4 水泵性能曲线Fig.4 Pump Performance Curve
根据各个水泵的性能曲线图,可得到额定转速下,水泵的一系列效率η0、流量Q0、扬程H0以及由此计算出的功率N0的离散值,即式(19)~式(22)。
再根据相似定律,可以得到任意调速比ki下,各水泵的功率Ni、流量Qi、扬程Hi,即式(23)~式(25)。
再搭建监督学习神经网络:在PyTorch 框架下,搭建2 层全连接层,各层的神经元个数为128,各层间激活函数为ReLU 函数。 其工作原理如图5 所示。
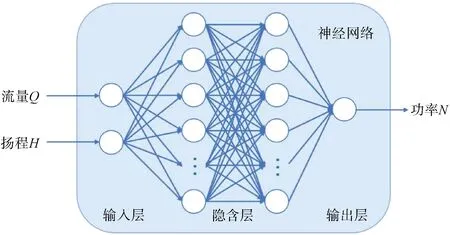
图5 监督学习神经网络工作原理Fig.5 Principle of Supervised Learning Neural Networks
从而可得到功率N关于流量和扬程的非线性关系模型,即式(26)。
为验证模型效果,本文通过式(27)计算出每台水泵在不同流量与扬程下的效率η,并在Matlab 软件中绘制曲面图,其结果如图6 所示。
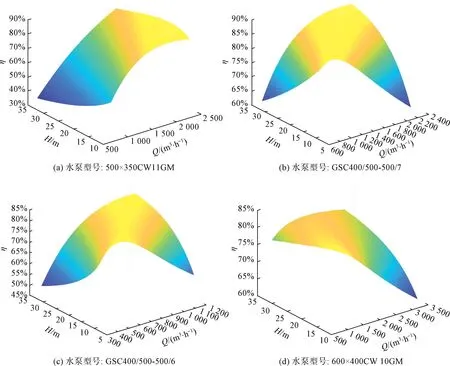
图6 效率-流量和扬程拟合关系曲面(4 种水泵)Fig.6 Fitting Relationship of Efficiency-Flow and Head (Four Kinds of Pumps)
其中:ρ——提升液体的密度,kg/m3;
g——重力加速度,m/s2。
由图6 可知,水泵的效率均位于40%~90%,结果符合实际情况;而水泵高效区要求效率为70%以上,为程序调节水泵至高效运行区提供了操作空间。
2.2.3 设置DQN 参数
本文所使用的深化学习工具为PyTorch,设置的状态空间包括5 台水泵的流量和水泵组提供的扬程H,动作空间为调节各个水泵的转速。 本文所涉及的估值网络和目标网络均采用深度神经网络(DNN)结构,隐藏层层数为3 层,每层128 个神经元,层与层之间的激活函数采用ReLU 函数。 超参数设置如表3 所示。

表3 超参数设置Tab.3 Hyperparameter Settings
3 网络训练及其结果分析
3.1 水泵组状态调控结果分析
图7 代表在智能体离线学习过程中,均方损失函数的变化情况。
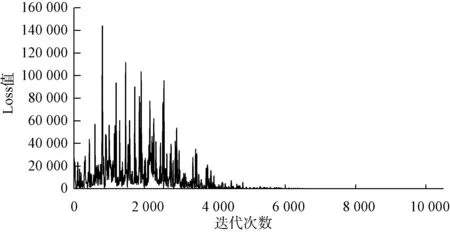
图7 均方损失函数变化Fig.7 Changes of Mean Squared Loss Function
损失函数指神经网络训练过程中预测值与真实值之间的差距,在本问题的研究中,网络预测值为各状态下的动作价值。 可将损失值反向传播,以更新网络权重。 由图7 可知,随着训练迭代次数的增加,均方损失函数逐渐减小至0,并保持不变,说明深度神经网络逐渐接近行为值函数,智能体可学习出最优策略。
为了检验学习结果,本文将上述训练完成的网络保存后,选取水厂周供水数据的第6 ~7 d 部分作为测试集,运行结果如图8 和图9 所示。
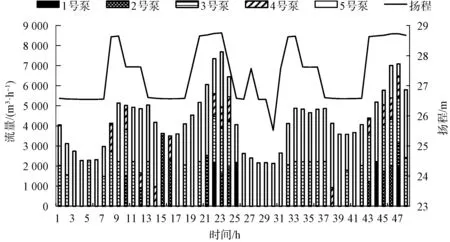
图8 水泵组运行状态变化Fig.8 Changes of Running State of the Pumps
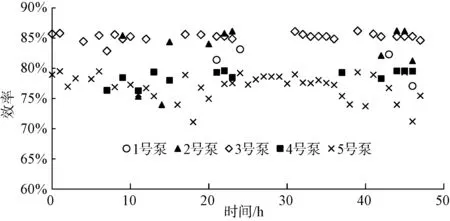
图9 运行中的水泵的效率变化Fig.9 Efficiency Changes of Running Pumps
图8 为不同时间段的水泵组运行情况,包括各水泵提供的流量和扬程,其中供水需求(总流量和扬程)的改变间隔为1 h。 智能体在需求改变后自动调整各变频泵的转速,在满足供水需求、各水泵均在高效区工作的基础上,使得水泵组总效率尽可能高。
图9 为各水泵在不同时间段的效率。 不同时间段上运行的水泵最低效率为70%,说明水泵的性能良好。 同时,在运行过程中,1 号、3 号、4 号水泵的效率均大于其最高效率的90%,说明水泵均处于高效区。 而波动较大的2 号泵,由图9 可知,其在运行过程中的效率为水泵效率的86.2%~74.0%,即最高效率为水泵效率的86.2%,运行中的最低效率是最高效率的85.8%,未处于水泵的高效区,还需优化。
3.2 对比分析
为说明DQN 算法的有效性,本文在相同供水需求的前提下,将人工调控与DQN 调控两种方式下的水泵组在不同时间段的功率消耗进行对比。 人工调控主要通过监测管网控制点的水压,通过比较实时水压与设定水压的差值,适当对部分水泵进行启停控制,以确保水泵在正常运行范围内,满足水压水位等要求。 由于上文所计算的效率为水泵效率,而实际中需考虑电机效率对水泵组总效率的影响,本文需对电机效率进行设定。 由于给水泵站的电动机铭牌效率普遍大于90%[12],本文设电机效率为90%,并由此计算水泵组在各时间段消耗的总效率。 对比结果如图10 和表4 所示。
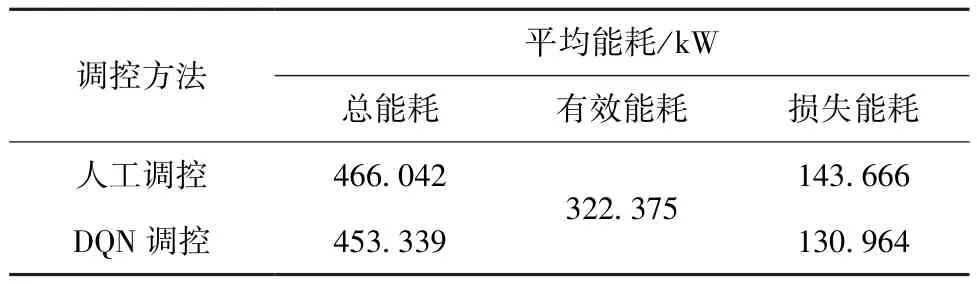
表4 调控结果对比Tab.4 Comparison of Control Results
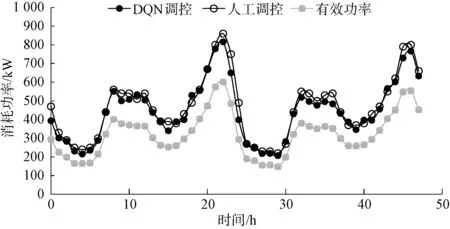
图10 调控结果对比Fig.10 Comparison of Control Results
由表4 可知,若采用人工调控,则泵组平均总消耗功率为466.042 kW;若采用DQN 算法调控,则泵组平均总消耗功率为453.339 kW。 而平均有效功率为322.375 kW,故两种方法的平均损失功率分别为143.666 kW 和130.964 kW,即DQN 算法相较于人工调控降低了8.84%的损失能耗。 在此节能效果下,该水厂一年可节省电耗1.11×105kW·h,即节省吨水电耗1.27×10-2kW·h/t。
由此可见,DQN 算法应用在给水领域,节能效果良好,不仅满足用户端的用水需求,且使各水泵均处于高效区工作,具有良好的经济效能,有效降低了泵站的运行能耗。
4 结论
针对水泵的流量和扬程在数值上连续变化的特点,首次将适应于连续状态空间的DQN 算法应用在给水领域,适应性良好。 根据用户的实时用水需求,通过DQN 算法快速求解出最优的水泵组合与流量分配,从而确定各水泵转速,节省人力资源,减少工作人员未及时调控的风险,提高供水服务水平。 同时,由于引入了经验回放池,DQN 算法能在运行过程中实时更新模型,针对不同的供水需求和其他环境变化,实现在线学习。 在本文的计算条件下,相较于人工调控,DQN 算法调控降低了8.84%的损失能耗,一年可节省吨水电耗1.27×10-2kW·h/t,实现了节能减排,具有良好的经济效能,说明基于DQN 算法的泵站供水系统最优节能控制方法具有较强的可推广性和实用性。

