位移电流测试方法的改进及应用

纪文宇　张汉壮

摘 要 自从麦克斯韦第一次提出位移电流这一概念之后，其在薄膜表征中便得到广泛的应用。然而，在课堂教学中，极少涉及位移电流的测试原理及相关应用讲解，更缺少对其实际应用的介绍。本文从位移电流的测试原理出发，联系实际应用，提出了基于周期性阶跃电压驱动的电流测量（CPSIV）的新方法。这将有效地加深学生对于位移电流物理本质的深入理解。同时，我们以量子点发光二极管（QLED）为平台，对这一新的测试方案进行了实验验证。针对其中空穴传输层薄膜的缺陷特性及其对器件性能的影响进行了表征，揭示了器件的发光开启机制，证实了我们方案的可靠性。

关键词 麦克斯韦方程;位移电流;周期性阶跃电压;长寿命缺陷态;量子点发光二极管

电磁场的规律经过麦克斯韦全面的总结，形成了用以解决各种宏观电磁场问题的麦克斯韦方程组[1]：

其中?D／?t 是位移电流密度。位移電流的引入成功地解决了安培环路定理在非恒定情形下遇到的矛图1 类平行板电容器器件位移电流测试示意图（a） 常规位移电流测试原理; （b） 薄膜中存在缺陷的情况; （c） 位移电流测试驱动电压及缺陷评估原理盾，使得电磁场形成了真正的统一理论[1]。位移电流的本质是电场随时间的变化。在实际应用中，对于半导体薄膜，由于缺陷的存在，经常通过位移电流测量来评估其中缺陷态的特性[2-3]。当使用位移电流测量法来表征半导体器件时，通常的做法是对器件施加周期性三角波电压，获得相应的电流密度。基本原理如图1（a）所示，模型器件由两相对电极及中间的半导体薄膜构成，类似于平行板电容器。设器件的几何电容及半导体薄膜厚度分别为C 和d，对器件施加偏置电压V，则器件靠近电流表一侧的电荷量Q'可表示为

-Q'=CV （5）

如图1（b）所示，当器件内部距离电极x 位置有一正电荷（电荷量为q）时，器件靠近电流表一侧的电荷量Q 可表示为

对上式进一步分析运算可得器件表面电荷密度σ 为

其中Cu 为单位面积电容，A（x）为电荷感应效率，n（x，t，V）为自由载流子密度，ρ 为被缺陷捕获载流子密度。即，公式（7）右边第一项为器件几何电容引起的位移电流，第二项为自由载流子及介电层中的缺陷对位移电流的贡献。此外，实际测得器件的总电流itotal 为位移（displacement）电流密度idis 与传导电流密度之和，是时间t 和电压的函数。当器件处于准静态时，忽略传导电流，idis 为

按照公式（7），当首次测量器件时，半导体薄膜中存在缺陷捕获过程，即ρ 对电荷密度σ（进而位移电流idis）有贡献。而在接续的第二次测量中，这一捕获过程的影响大大降低。所以，所得位移电流的大小会有差值，如图1（c）所示。两次位移电流的差值可以反映器件中缺陷态的信息，其中σinj为第一次注入的电荷密度， σext 为反向扫描时抽取出的电荷密度，σtrap 为缺陷俘获的电荷密度。

1 位移电流测试方案的改进

以上对于半导体薄膜缺陷态的表征无法体现缺陷态寿命的信息，即无法评估不同寿命的缺陷态对器件性能的影响。为此，我们提出利用周期性阶跃式上升三角波电压代替传统线性三角波电压，如图2（a）所示，驱动电压周期为T 。通过调控阶跃电压的步长Δt 及ΔU ，可以获得时间分辨瞬态电流特性。图2（b）为某一电压下连续两次扫描器件电流测试结果。RC 所示部分为器件的电容充电过程，我们这里定义充电时间大于5RC（R 为电路等效电阻，C 为等效电容）时为稳态。由图可知，第二次扫描得到的电流明显低于第一次扫描得到的电流，如前所述，这是由于缺陷态的影响。通过选取tn 与tn+5RC 之间任意时刻的两电流值做差，我们可以得到不同缺陷态寿命电流特性的影响。这一结果证实，在实际的位移电流测试中，需要针对具体薄膜特性来有针对性地对驱动电压的模式进行设计，以得到更加真实的薄膜缺陷信息。在相关教学中向学生讲解这一原理是必要的，一方面使其对位移电流的本质及其测试有更加深入的了解，同时也为学生在以后的相关实验及科研中对相关数据的分析提供理论支撑。

2 半导体薄膜中缺陷态及其对电流影响分析

近年来，半导体材料及光电器件得到迅速发展，成为科技的制高点。在实际的半导体中，某些区域的晶体结构由于遭到破坏并不完整，会形成各种形式的缺陷[4]。在某些情况下，缺陷对半导体材料的光电性能起着积极的作用[5]。例如，氧化锌（ZnO）和二氧化锡（SnO2）纳米粒子薄膜的电荷输运行为受Mott变程跳跃过程影响，即电荷载流子主要通过ZnO 和SnO2 纳米晶体中的缺陷态传输[6];在AgInS2 和CuInS2 量子点中，缺陷态也可以成为发光中心[7]。然而，在大多数情况下，缺陷的存在会降低半导体薄膜的性能[8]。缺陷引起的载流子俘获效应降低了自由载流子浓度，从而降低了载流子迁移率[9];同时，对于光电器件来说，空间电荷区的电子空穴会通过缺陷态发生非辐射复合，随着缺陷态密度的增加，器件的辐射效率将会降低[10]。因此，研究半导体材料中缺陷的相关信息对于优化半导体薄膜和提高光电器件性能起着至关重要的作用。位移电流测量法是研究半导体器件中电荷载流子动力学的一种简单有效的方法[11]。

根据缺陷态能级的深浅不同可分为浅缺陷态和深缺陷态。浅缺陷态为能级接近导带或价带的缺陷态，它能够捕获附近经过的载流子。被捕获的载流子由于热运动会重新回到导带或价带中继续参与传输。因此，这个过程中会显著降低载流子的传输速度[12]。但是，在一些氧化物无定型薄膜如ZnO 接SnO2 纳米晶体薄膜中，电荷载流子是通过浅缺陷态之间以Mott变程跳跃的方式进行传输的[6]。一般被深缺陷态捕获的电荷载流子会长时间地存在于缺陷能级中，这些载流子将会对后续注入的电荷载流子产生库仑排斥作用，从而降低载流子的迁移率，所以它们是影响薄膜准稳态时电学特性的主要来源。

3 器件制备及测试系统

我们制备了结构为ITO/ZnO （40nm）/QDs（25nm）/4，4'，4″-Tris（N-carbazolyl）-triphenylamine（TCTA，60nm）/MoO3（8nm）/Al（100nm）的倒置QLED器件，如图3所示。首先，将带有图案的ITO 玻璃基片依次用丙酮、无水乙醇、去离子水分别超声清洗15 分钟后，用氮气吹干，再把ITO 玻璃基片放到紫外臭氧清洗机中照射处理15 分钟，以增加ITO 表面的润湿性。之后在充满氮气的手套箱中沉积ZnO 及QD 薄膜。ZnO 及QD薄膜通过溶液旋涂工艺制备，转速为2500r/min，旋涂时间为1分钟。ZnO 及QD薄膜旋涂之后分别在120℃和80℃下热处理30分钟。最后将带有ZnO及QD薄膜的衬底转移到真空蒸镀室内，在压强低于4.5×10-4Pa的条件下沉积空穴传输层TCTA（60nm）、空穴注入層MoO3（8nm）和金属Al电极（100nm）。利用紫外固化胶和盖玻片对器件进行简单封装，并在空气中完成相应的光电测试。器件的电流密度电压亮度（J-V-L）特性通过Keithley 2400型数字源表和光度计LS-110进行测试，器件电容特性通过LCR 测量仪（Precision LCR Meter TH2829C Tonghui）获得。

上述的ZnO 纳米颗粒按照文献方法合成[13]，并溶于无水乙醇溶剂中，浓度为40mg/mL。所用Zn（CH3COO）2 ·2H2O 及KOH 购买于天津百伦斯生物技术有限公司，CdSe/ZnS QDs（甲苯溶剂，浓度为12mg/mL）量子点购于纳晶科技公司。

4 结果与讨论

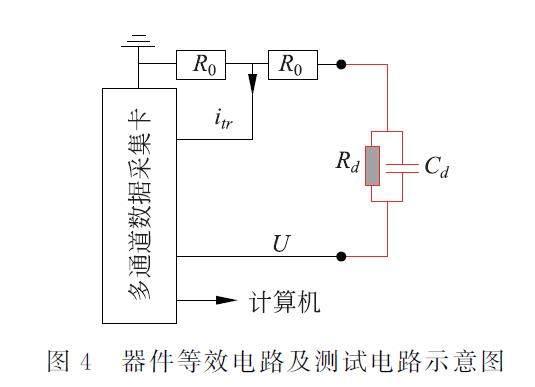
按照文献报道[14]，QLED 可以用一个电阻和一个电容并联组成的等效电路来代替。如图4所示，在测试电路示意图中，RS 代表由电极和导线等引起的串联电阻，R0 为分压电阻，用以测试器件的电流及电压。电压的输出及测量由多功能数据采集卡（PCIe-6321）来完成。通过PCIe-6321的模拟输出通道（AO 通道）提供阶跃电压的输出，PCIe-6321的差分输入可以测量电压。所采集的数据为不同驱动电压下电阻R0 的电压，根据电阻R0 的值就可以算出通过QLED 器件的电流。

由于QLED器件可以看作RC元件，当QLED 器件中的载流子复合、缺陷态捕获等载流子动力学过程可忽略时，结合图2（a）所施加的驱动电压，根据戴维宁定理就可以得到在第n 个阶跃电压（tn＜t＜tn+△t）下经过QLED 器件的瞬态电流响应itr（t）的表达式：

其中，Re 是戴维宁定理中的等效电阻，Cd 和Rd分别为器件的等效电容和等效电阻，可以通过测试器件的阻抗谱得到。公式（9）中第一项代表器件的稳态（steady state）电流iSS （t），第二项为器件的位移电流iRC （t）。iRC （t）对器件的电流变化具有重要贡献，当分析器件中长寿命缺陷态的特性时，应当排除位移电流iRC （t）的影响。一方面，由于iRC （t）在经过5ReCd 的时间后会下降至最大值的0.67%，所以选取tn +5ReCd 时的电流作为器件在该阶跃电压的电流来研究缺陷态问题，则阶跃电压持续时间Δt 应当大于5ReCd 。另一方面，由于缺陷态的填充时间在几百微秒至几秒的时间尺度内。当阶跃电压持续时间Δt 太大时，器件的长寿命缺陷态在第一周期内前一部分阶跃电压将被基本填满，使得第一周期和第二周期的电流基本相同，所以阶跃电压持续时间Δt 也不能过大。在实际测试中，我们一般取阶跃电压持续时间Δt 为10ReCd 左右。同时，对于阶跃电压高度ΔU 来说，为了更加细致地描述载流子动力学过程，ΔU需要取得适当小，一般取阶跃电压高度ΔU 为0.05V。

在选择R0 之前，先对QLED 进行阻抗谱测试，获得器件的等效电阻Rd 和等效电容Cd ，其分别为5492kΩ和1.80nF。因此，分压电阻R0 设定为100kΩ，根据公式（9）可得Re 为98.2kΩ。则5ReCd 约为0.9ms，本实验中阶跃电压持续时间Δt 设置为2ms。

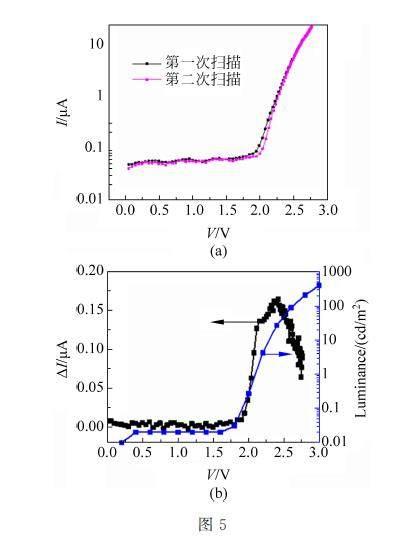
图5（a）为对QLED 器件连续两次扫描所得电流电压（I-V ）曲线。可以明显看出，驱动电压在2.0V～2.5V 之间时，第一次扫描所得电流与第二周期电流存在差异。就像前文分析的一样，这是由器件中的长寿命缺陷态所造成的。为了更好地分析长寿命缺陷态引起的电流变化，我们将同一电压下第一周期的电流减去第二周期电流得到第一、二周期电流差随电压的变化，如图5（b）所示。可以看到随着电压增加，器件中会出现明显的电流差。在QLED器件中，电子传输层ZnO以及量子点层中的缺陷态主要为浅缺陷态[15]，对电流差的贡献很小。所以QLED器件中的长寿命缺陷态应该来自空穴传输层TCTA，即电流差的出现是因为空穴传输层的长寿命缺陷态捕获空穴所引起的。

在图5（b）中，我们还应当注意到随着电压的增加，电流差会出现一个峰值。这是因为在第一周期阶跃电压上升的过程中，器件中的长寿命缺陷态将不可避免地捕获载流子而引起散射效应，使得第一、二周期的电流越来越接近。因此，电流差将会随着电压的增加出现峰值甚至下降。对于不同材料结构的器件来说，其中的缺陷态会有显著不同，长寿命缺陷态越多对器件电流的影响就越大，所测电流差的峰值也会相应增大，所以器件电流差的峰值可以一定程度上表征器件中长寿命缺陷态的多少。

如前所述，由于第一、二周期的电流差是因为空穴传输层的长寿命缺陷态捕获空穴导致的，所以电流差突增时的电压代表空穴的注入电压，即，此时空穴开始大量注入到器件当中，与量子点中注入的电子形成激子，导致发光。根据图5（b）中的电流差―电压变化曲线可知，所测QLED 器件的空穴注入电压约为2.0V，与QLED的开启电压（亮度为0.1cd/m2 时的电压）一致。因此，我们完全可以推断QLED器件的电致发光开启是由空穴注入所决定的。

5 總结

我们根据麦克斯韦所提出的位移电流概念，结合实际半导体薄膜的特性，通过改变驱动电压模式，建立了基于周期性阶跃电压的位移电流相关表征方法，用以评估薄膜中的长寿命缺陷态，并利用多层薄膜构成的器件进行了验证。实验结果与我们的理论结果一致。同时，利用此种测试原理，还揭示了器件中电致发光开启电压的特性，即，QLED器件的电致发光开启由空穴注入电压决定。因此，我们相信此研究方法也能够对其他光电子器件中的长寿命缺陷态进行表征。此测试系统还有进一步的优化空间，例如，将多功能数据采集卡更换为具有更高电压分辨率和电流分辨率的设备，可以表征更短时间尺度的缺陷态。

参考文献

[1] 赵凯华，陈熙谋. 电磁学[M]. 北京：高等教育出版社，2011.

[2] MONTERO J M， BISQUERT J. Interpretation of trap-limitedmobility in space-charge limited current in organic layerswith exponential density of traps[J]. J.Appl.Phys.， 2011，110（04）：3705-3710.

[2] QIU X C， LIU Y， HU Y Y. Traps in metal halide perovskites：Characterization and passivation[J]. Nanoscale，2020， 12（44）： 22425-22451.

[4] 刘恩科，朱秉升，罗晋生. 半导体物理学[M]. 北京：电子工业出版社，2017.

[5] WANG J P， GREENHAM N C. Charge transport in colloidal ZnO nanocrystal solids： The significance of surface states[J]. Appl.Phys.Lett.， 2014， 104（19）：1-5.

[6] WANG Y C， ZHU X X， JI W Y， et al. Electron transport mechanism in colloidal SnO2 nanoparticle films and its implications for quantum-dot light-emitting diodes[J]. J.Phys.D： Appl.Phys.， 2022， 55（37）：4004.

[7] LI L， PANDEY A， WERDER D J， et al. Efficient synthesisof highly luminescent copper indium sulfide-based core/shell nanocrystals with surprisingly long-lived emission[J].J.Am.Chem.Soc.， 2011， 133（5）： 1176-1179.

[8] LI C， DUAN L， QIU Y， et al. Universal trap effect in carriertransport of disordered organic semiconductors： Transitionfrom shallow trapping to deep trapping[J]. J.Phys.Chem.C， 2014， 118（20）：10651-10660.

[9] LI H Y， LI C， DUAN L， et al. Charge transport in amorphousorganic semiconductors： Effects of disorder， carrierdensity， traps， and scatters[J]. Isr.J.Chem， 2014， 54（7）：918-926.

[10] NEAMEN D A. 半导体物理与器件[M]. 4版. 赵毅强，姚素英，史再峰，等. 北京：电子工业出版社，2018.

[11] NOGUCHI Y， ISHII H， KIM H J， et al. Device propertiesof Alq3-based organic light-emitting diodes studied bydisplacement current measurement[J]. J.Photon.Energy，2012， 2（1）： 021214.

[12] ZHU X X， WANG Y C， JI W Y， et al. Unraveling theTurn-On Limitation of Quantum-Dot Electroluminescencevia a Stepwise-Increasing Voltage Measurement[J]. Phys.Rev.Appl.， 2023， 19（2）： 4010.

[13] KWAK J， BAE W K， LEE D， et al. Bright and efficientfull-color colloidal quantum dot light-emitting diodes usingan inverted device structure[J]. Nano Lett.， 2012， 12（5）：2362-2366.

[14] XU L， WANG J， HSU J W P. Transport effects on capacitance-frequency analysis for defect characterization in organicphotovoltaic devices[J]. Phys.Rev.Appl.， 2016，6（6）： 4020.

[15] WANG F F， HUA Q Z， JI W Y， et al. High-performanceblue quantum-dot light-emitting diodes by alleviating electrontrapping[J]. Adv.Opt.Mater.， 2022， 10（13）：2200319.