基于固有可靠度和使用可靠度的干线协调效果评价
白 翰,王修光,黄洪科,王国军,燕 翔
(1. 山东交通学院 交通与物流工程学院,山东 济南 250357; 2. 山东正衢交通工程有限公司,山东 济南 250013;3. 山东天为工程技术有限公司,山东 淄博 255000)
0 引 言
我国城市交通管控水平有限,道路交通管理设施不足,交通参与者的整体交通素质不高,各种交通流之间干扰严重,导致城市交通信号控制具有高度的复杂性和不确定性[1]。如何准确量化干线协调控制方案实施前的适用性,分析判断干线协调控制方案实施后的效益性,是当前城市交通信号控制存在的现实问题。
为了获得较好的干线协调效果,学者们基于不同的控制目标来寻找最佳的协调控制方案。J.D.LITTLE等[2]将相位差、周期时长、行驶车速、相位相序等要素综合考虑,以双向绿波为最大目标,提出了一系列干线协调控制模型;YANG Xianfeng等[3]提出一种可涵盖多条大流量路径的协调优化模型。在此之上,学者们将延误[4-6]、排队车辆数[7]、安全[8]、减少排放[9]等多种指标[10-12]作为协调目标建立了干线优化模型;赵欣等[13]在公交优先的场景下提出了一种干线协调模型,能最大限度地增加公交车不停车通过交叉口的概率;鄢小文等[14]考虑车队离散因素,提出路径可协调度的概念,建立了干线协调的两节点关联性模型。
近年来,学者们开始关注干线协调控制中的信号控制方案实施后的评价和改进。如:卢凯等[1]通过对车速的数据样本与概率分布进行分析,制定了绿波协调控制方案的评价与设计标准;林强等[15]研究了从干线交叉口结构、运行质量、交通安全和环境影响等4方面形成相对完整的线控制评价集,得出了能反映线控制系统实施后的运行效果优劣的结果;丁建梅等[16]以车均延误、排队长度、停车次数、空气污染指数作为评价指标,对用VISSIM仿真手段所获取的基础数据以置信度准则方法确定了控制效果的评价向量;冯宣东[17]研究了“跟车法”计算机辅助调查系统,收集了配时参数、检测和评价信号配时效果,并作为评价和优化信号配时的方法;韩伟帅[18]基于云模型,研究了绿波协调控制方法的适用性与效果性评价。在交通可靠性研究中,学者们更多的是对连通可靠度[19]、运行时间可靠度[20]、容量可靠度[21]、畅通可靠度[22-23]等方面展开。
在干线协调控制效果评价方面,卓曦等[24]从绿波系统效率与安全指标出发,提出了一种绿波协调控制系统灰色关联评价方法;魏向达等[25]以车辆轨迹数据为基础,在保证评价方法简便可操作的基础上实现了对不同绿波方案的评价。以上研究大多是单独考虑干线协调的可实施性或效益性,较少考虑实施前的适用条件与实施后效果相结合的一体化可靠性评价,且当前研究多借助较为复杂的计算方法进行评价,难以广泛应用。
基于此,笔者充分考虑了干线协调控制方案实施前、后的适用性与效益性之间的联系,为提高评价方法时效性、普及性、便捷性,针对干线协调控制效果可靠性的内涵,结合速度、交通流量、停车次数、绿波带宽等表征参数,建立了干线协调控制效果可靠性的综合评价体系,为更可靠的干线协调控制效果设计提供支持。
1 干线协调可靠度定义
可靠度是指单元或系统在规定使用期间和预定工作条件下,能够满足预定功能的概率[22]。按照产品工作可靠性的定义,可分为固有可靠度和使用可靠度。按照可靠性规划,可分为原材料及零部件选用、自身固有效果及使用效果等所确立的可靠性[26]。
笔者从固有可靠度和使用可靠度两方面出发,对干线协调控制实施前的路段适应条件与实施后的路段控制效果进行评价。固有可靠度(布设前)可定义为:在当前交通流条件下,能实现干线协调控制方法的可靠性,主要受道路交通流量、速度及车辆密度影响;使用可靠度(布设后)可定义为:在当前交通流状态和实现干线协调控制方法具备一定可能性的条件下,经信号控制优化设计后,实际运行中的干线协调控制能达到与设计理想效果相接近的可靠性,其主要由使用效果指标与设计效果指标的差值大小决定。
2 干线协调控制效果可靠性模型
根据相关资料和专家咨询,对干线协调控制效果的绿波带宽进行定量划分可靠性的临界值。认定当某个方向上的绿波带宽达到或超过原设计绿波带的25%,则认为该双向干线协调控制效果没有实现,说明该控制效果处于不可靠状态,需要再次进行设计或单向协调控制。故笔者借助该结论,展开以最大绿波带宽作为干线协调控制的目标,以固有可靠度和使用可靠度评价指标对干线协调控制效果影响临界值的确定及模型建立。
2.1 固有可靠度
固有可靠度主要由交通流秩序决定,其中速度与交通流量是决定交通流秩序的重要因素。当车辆实际速度变化较为频繁或剧烈时,会导致道路实际平均车速也发生较大波动,从而使得实际平均速度与设计平均速度产生较大差异,干线协调控制系统的绿波带宽也会有较大波动,导致实际干线协调控制效果降低。当实际交通流量与设计交通流量产生差异时,同样会影响干线协调控制的固有可靠度,主要表现在当实际交通流量大于设计交通流量时,会导致以设计绿波带宽行驶时存在小部分交通量无法正常通过;当实际交通流量小于设计交通流量时,虽以设计绿波带宽行驶能保证车辆全部通过,但会出现部分绿波时间冗余和浪费现象。因此,笔者选取平均速度与交通流量作为干线协调控制效果固有可靠度评价指标。
2.1.1 平均速度临界值确定
在其他条件不变情况下,根据绿波带宽临界的结论,采用图解法与控制变量法,假设以40km/h作为车辆在干道行驶的理想速度,通过不同的平均速度值,对续进协调方式下的干线绿波带宽的影响进行分析,如图1。
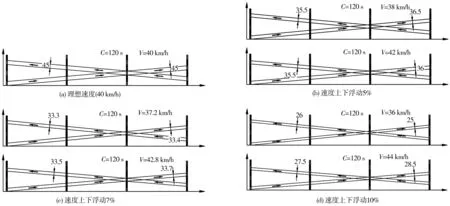
图1 干线信号协调示意Fig. 1 Schematic diagram of arterial signal coordination
由图1(b)~图1(d)可知:绿波带宽随着平均速度的增加而不断减小,当减小至理想绿波带宽的75%时,其相应平均速度浮动值为7%,与已知结论中绿波带宽变化为原来设计绿波宽度25%的临界值相对应。为保证实验准确性,针对理想速度为60、80 km/h的干线协调控制分别进行平均速度上下7%的浮动,发现与已知结论中绿波带宽变化为原来设计绿波宽度25%的临界值相对应,如图2。故当平均速度上下浮动数值范围在[-7%, 7%]时,干线协调控制效果的固有可靠度较高且满足条件,反之,则固有可靠度较低且无法满足条件。
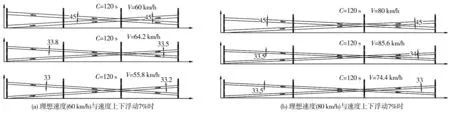
图2 干线信号协调示意Fig. 2 Chart of arterial signal coordination
2.1.2 交通流量临界值确定
当道路交通流为设计交通流量时,单位小时内在绿波时间内可通过的交通量为Q,如式(1):
(1)
式中:S为路段的饱和流率,pcu/h;B为干线协调控制绿波带宽,s;T为公共周期,s。
由绿波带宽的最大减小时间(或空余时间)为绿波带宽25%结论推导可知:若要保证干线协调控制效果的固有可靠度处于可靠范围,则协调相位变化的交通流量最大值为ΔQ,如式(2):
(2)
综上,可认为在其他条件不变情况下,当协调方向的交通量在[-25%, 25%]时,干线协调控制效果的固有可靠度较高且满足条件;反之,则固有可靠度较低且无法满足条件。
交通量和速度变化直接影响干线协调控制效果的固有可靠度。为更直观地表达交通量与速度的离散程度,利用实际平均速度及实际平均交通流量与设计平均速度及设计交通流量之间的差值来表示其离散度,如式(3)、 式(4):
(3)
(4)
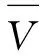
借助干线协调控制效果评价公式,鉴于fv有超过[-7%v, 7%v]的可能,为直观清晰地表达速度与其具体可靠度之间关系Kv,如式(5)。
(5)
同理,交通量与其具体可靠度间之间关系Kq可由式(6)表示。
(6)
为量化交通量与速度对干线协调控制固有可靠度的影响,笔者利用层次分析法,对照准则进行分析,如表1。制作了影响因素相对重要程度调查表,共20份;利用专家经验法对接触过干线协调控制工作或研究的专家等进行调研;通过数据整理、归一化、判断矩阵权重与特征值计算,得到速度权重值α和交通量权重值β,如表2。当影响因素数目n≥3时,方可进行一致性检验,而文中固有可靠度影响因素仅有交通量与平均速度,故无需进行一致性检验。

表1 层次分析法可靠性指标重要程度等级及含义
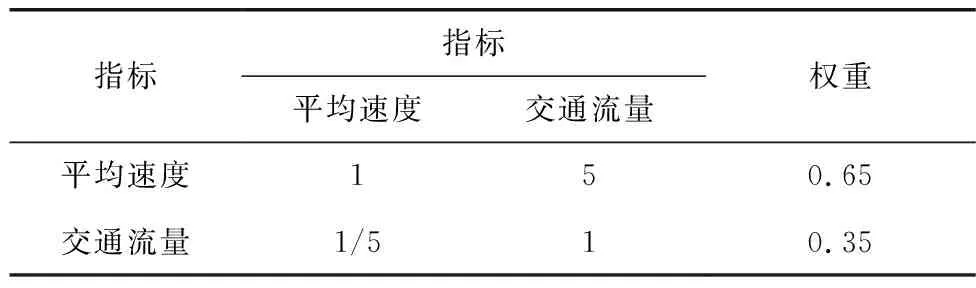
表2 指标重要度及权重值
由各项影响因素权重值,结合可靠性影响分析结论,笔者提出了干线协调控制效果固有可靠性的目标函数,如式(7):
K1=αKv+βKq
(7)
式中:α、β分别为影响因素的平均速度和交通量权重值;K1为干线协调控制效果固有可靠度。
根据城市道路基本路段服务水平划分方式,提出干线协调控制效果固有可靠度评判级别,如表3。

表3 干线协调控制效果固有可靠度等级
2.2 使用可靠度
干线协调控制是指当车辆沿某条干道行驶过程中,连续获得多组的绿灯信号,因此保证车辆在沿线交叉口连续通过是考察干线协调控制效果的重要指标。故笔者选取停车次数作为使用可靠度的初步检验指标,并认为当实际停车次数与设计停车次数完全一致时,可认为干线协调控制使用可靠度满足条件;反之,则无法满足条件。其初步检验指标如式(8)。
K2≤0 (n≠0时)
(8)
式中:n为实际与设计停车次数差值;K2为干线协调控制效果使用可靠度。
当n=0时,可认为使用可靠度能初步满足条件,其可靠度仍受绿波带宽影响。故笔者在此基础上,借助绿波带宽影响因素对使用可靠度能否满足条件进行最终评价。
当实际协调效果与设计协调效果相差过大时,与设计绿波宽度相比,这二者差值在[-25%, 25%]之外时,此时干线协调控制的使用可靠度无法通过,且为负值;反之,则使用可靠度可通过。基于此,笔者提出了一项干线协调控制效果使用可靠性的评价函数,如式(9):
(9)
式中:Co为设计绿波带宽,s;C为实际绿波带宽,s;ΔC为实际绿波带宽与设计绿波带宽绝对值,s。
根据城市道路基本路段服务水平划分方式,提出了干线协调控制效果使用可靠性的评判级别,如表4。

表4 干线协调控制效果使用可靠度等级
2.3 可靠性综合评价模型
针对续进式的干线协调控制方案,笔者提出了在应用前后的干线协调控制效果综合评价方法,建立了基于固有和使用可靠度的干线协调控制效果可靠性综合评价模型,评价函数如式(10)。
(10)
3 干线协调控制可靠度应用
笔者选取济南市的烟台路与齐州路、烟台路与腊山河东路和烟台路与腊山河西路交叉口为实例,进行干线协调控制效果可靠性综合评价,评价时间为周三09:00—10:00的平峰时段。
3.1 固有可靠度评价
笔者利用试验车法获取了各交叉口的交通量、平均速度,并进行固有可靠度评价。齐州路—腊山河东路的平均速度标准差由西至东为0.49 km/h,由东至西为0.59 km/h;腊山河西路—腊山河东路的平均速度标准差由西至东为0.46 km/h,由东至西为0.38 km/h。齐州路—腊山河东路的平均速度可靠性Kv由西至东为0.81,由东至西为0.79;腊山河西路—腊山河东路的平均速度可靠性Kv由西至东为0.82,由东至西为0.86。烟台路与齐州路的协调相位交通流量标准差由西至东为71辆/h,由东至西为72辆/h;烟台路与腊山河西路的协调相位交通流量标准差由西至东为60辆/h,由东至西为65辆/h;烟台路与腊山河东路的协调相位交通流量标准差由西至东为65辆/h,由东至西为63辆/h。烟台路与齐州路交叉口协调方向交通流量可靠性Kq由西至东为0.35,由东至西为0.39;烟台路与腊山河西路交叉口协调方向交通流量可靠性Kq由西至东为0.41,由东至西为0.46;烟台路与腊山河东路交叉口协调方向交通流量可靠性Kq由西至东为0.58,由东至西为0.56。
由此可知:烟台路(齐州路—腊山河东路)各方向平均速度与交通量的可靠度均大于0且较高,无需对交通流进行整顿,取各方向平均速度可靠度的平均值作为最终平均速度可靠度即可;最终平均速度可靠度为0.82,交通量可靠度为0.46。
由式(7)可知:烟台路(齐州路—腊山河东路) 干线协调控制效果固有可靠度K1=0.69,为一般可靠。
3.2 使用可靠度评价
经多次设计及审核,最终烟台路(齐州路—腊山河东路)的设计协调效果为:双向绿波不停车,东向西绿波带宽为42 s,西向东绿波带宽为40 s。方案经检测后实际效果为:双向绿波不停车,东向西绿波带宽为39 s,西向东绿波带宽为38 s,如表5。由表5可知:设计停车次数与实际停车次数差值n=0,且设计带宽与实际带宽差值均在25%以内,协调效果基本达到;由式(9)可知:双向使用可靠度分别为0.72、0.80,取平均值后的可靠度为0.76,即烟台路协调效果使用可靠度K2=0.76,为可靠。

表5 烟台路(齐州路—腊山河东路)设计效果与实际效果统计
综上,烟台路(齐州路—腊山河东路)的固有可靠性为一般可靠,能够且适合进行干线协调控制方案设计,干线协调控制效果容易实现。方案实施后,实际效果与协调效果基本一致,干线协调控制方案使用可靠度达到预期。
4 结 语
笔者通过量化行驶速度、交通流量、停车次数、绿波带宽等表征参数,提出了干线协调控制效果的固有可靠度与使用可靠度评价方法;构建了干线协调可靠性综合评价体系;以济南市为例,评估了干线协调控制方案的可靠度。研究结果表明:济南市烟台路的固有可靠性为一般可靠,适合进行干线协调控制方案设计,方案实施后,实际协调控制效果可靠。

