基于IWOA-BP的石英振梁加速度计温度补偿研究
张 晗,林盛受,毛志成,梁金星
东南大学仪器科学与工程学院
0 引言
石英振梁加速度计(quartz vibrating beam accelerator,QVBA)具有灵敏度高、功耗低和体积小等优点,因此适合应用在惯导系统中。使用振荡电路实现对加速度计谐振梁的起振,谐振频率的偏移体现出加速度的变化。后续针对输出信号的频率进行测量,不存在因模数转换环节而引入的转换误差[1],测量过程中也不易于受到环境噪声的干扰[2]。
目前针对加速度计等惯性器件的温度补偿主要包括硬件补偿和软件补偿。硬件补偿主要是从加速度计的结构设计、制造工艺、封装技术等方面进行优化,降低温度对加速度计的影响。硬件补偿方案可靠性较高,但研发周期较长,成本较大。软件补偿方案是通过重复性的温度实验,采集温度与输出漂移的数据,进而建立温度与输出漂移之间的模型。对整体系统而言,不会增加过多的功耗。软件补偿方案对建模的精度具有一定要求,补偿算法会具有一定的复杂性。
在加速度计软件温度补偿的研究方面,付红坡等[3]提出了一种基于改进减法聚类与自适应神经模糊推理系统相结合的温度漂移模型,将其运用在石英挠性加速度计中。M.Zhu等[4]提出一种基于卡尔曼滤波和遗传算法优化的径向基神经网络温度补偿方案,用于针对高g值加速度计的温度漂移建立模型。B.Li等[5]提出一种采用变系数回归和最小二乘支持向量机相结合的温度补偿方法,对谐振式加速度计进行温度补偿,并把模型导入FPGA以完成实时补偿。G.Guo等[6]提出一种基于改进麻雀搜索算法优化深度长短期记忆神经网络,实现了对MEMS加速度计的实时温度漂移补偿。
相较于硬件补偿,软件补偿同样可以具有较高的可靠性和稳定性。文中考虑到加速度计系统的功耗、尺寸,以及现有实验技术条件,采用基于软件误差建模的温度补偿方案。
1 石英振梁加速度计
1.1 QVBA基本组成
图1为QVBA结构示意图,包括谐振梁、质量块、铰链、支撑座、隔振框和安装框。

图1 石英振梁加速度计结构示意图
加速度计的敏感轴方向与质量块所处平面相垂直,在外界施加加速度作用于质量块上时,通过杠杆作用,惯性力被放大且被耦合到谐振梁上。当谐振梁收到拉/压力时,梁的谐振频率发生改变,通过对谐振频率的变化进行检测,即可得到系统所处环境的加速度值。
文中谐振梁在振荡电路的激励下可以工作在面内弯曲振动模态,梁的谐振频率可以由式(1)给出[7]:
(1)
式中:b为谐振梁的宽度;l为谐振梁的长度;ρ为石英晶体的密度;s为石英晶体的弹性柔顺系数;h为谐振梁的厚度;F为谐振梁受到的轴向力。
石英加速度计的谐振梁所受力F与外界加速度a之间存在的关系式如下:
(2)
式中:m为质量块的质量;L0为质量块重心到铰链中心的距离;L1为质量块厚度与谐振梁厚度之差;λ为常数,λ=2L0/L1。
式(1)也可以简化为
f=k0+k1a
(3)
式中:k0为加速度计的零位偏值;k1为加速度计的标度因数。
结合式(1)和式(2),可以推导得到k0、k1的表达式为:
(4)
(5)
1.2 QVBA的温度特性
温度变化对QVBA造成的影响主要体现在谐振梁的尺寸、石英晶体的密度和弹性柔顺系数的变化[8]。
由于谐振梁会因为环境温度的变化而产生热胀冷缩的现象,因而导致谐振梁的尺寸随温度发生变化。可以使用式(6)表示加速度计中石英谐振梁的线膨胀方程:
(6)

由于石英晶体并不是完全的各向同性,沿石英晶体Z轴方向的线膨胀系数与X轴和Y轴的线膨胀系数值不相等,即αx=αy≠αz。
石英晶体的密度ρ是温度的函数,可以使用式(7)表示加速度计中石英晶体的材料密度-温度特性方程:
(7)

石英晶体的弹性柔顺系数为sij,其中i、j表示石英晶体沿不同方向的弹性柔顺系数。石英的弹性柔顺系数会随着温度的变化而改变,类似的,弹性柔顺系数的温度特性方程可以表示为
(8)

经过上述分析,谐振梁的尺寸、石英晶体的密度和弹性柔顺系数都具有一定的温度特性,它们的改变会影响到零偏和标度因数的数值,从而造成输出误差。
虽然本文中采用的加速度计是差分式结构,即将2个含有敏感谐振梁的微结构集成封装,差分输出可以一定程度上减少共模干扰,并消除大部分的温度漂移。但由于制造误差、封装差异等因素,2根谐振梁的温度特性并不完全一致。因此,在全温实验环境下,仍需要采用温度补偿的方案来提升加速度计的稳定性。
2 温度补偿技术
2.1 加速度计温度补偿模型
目前,常用的加速度计温度补偿模型可以分为独立建模和统一建模的温度补偿模型[9]。
独立建模的温度补偿模型需分别建立零偏-温度模型和标度因数-温度模型,选取合适的数学模型进行拟合。该方案易于实现,但缺点在于二次建模相较于一次建模会引入更多的建模误差,所以使用时需要尽可能地减少建模误差,提高模型的准确性和可靠性。
统一建模的温度补偿模型是采用加速度计信号输出及温度传感器输出作为补偿模型的输入量,以离心转台真实设定的加速度a作为输出量,采集三者的数据进行拟合。该方案的优点是只需要一次建模,缺点是采集实验数据要进行加速度计量程范围内的温度实验,该环节需要高精度的温控离心转台设备,对实验设备的要求较高。
2.2 BP神经网络
人工神经网络是深度学习的基本组成部分,其思路是模仿人的大脑工作原理,人为构造出的一种数学模型。BP(back propagation)神经网络是人工神经网络的一种,它采用误差反向传播的方式更新神经元间的连接权重,所以称为BP神经网络。
BP神经网络具有3层结构,分别是输入层、隐藏层和输出层。因为隐藏层的激活函数选择非线性S型函数,使得模型具有了拟合非线性的能力,仅含一个中间层的神经网络能以任意精度逼近一个非线性函数[10]。因此,本文选择BP神经网络对温度补偿模型进行拟合,BP神经网络的结构图如图2所示。

图2 BP神经网络的三层结构
对于3层的BP神经网络,假使输入向量为:x=(x1,x2,…,xi,…,xn)T,输出向量期望值为:y=(y1,y2,…,yk,…,ym)T,Wij为输入层与隐藏层之间的连接权值,Wjk为隐藏层与输出层之间的连接权值。θ为隐藏层节点的阈值,η为输出层节点的阈值。φ、ψ分别为隐藏层、输出层的激活函数。各隐藏层节点的输出Pj可以由式(9)计算:
(9)
输出层节点的输出Ok可以由式(10)计算:
(10)
最终,可以得到神经网络模型输出值与真实数据值之间的误差函数E:
(11)
BP神经网络的训练目标是求取合适的权值和阈值,使累积误差函数值最小。通常的训练方法是采用梯度下降策略,即根据梯度下降的方向对网络的参数进行调整。
然而,BP神经网络在算法选取初始权值和阈值时具有一定的随机性,导致算法存在鲁棒性差和局部最优等问题,在一定程度上会影响到补偿模型的精度。因此本文采用改进鲸鱼优化算法(improved whale optimization algorithm,IWOA)对BP神经网络进行优化,使用IWOA算法对BP神经网络的最优初始参数进行全局搜索寻优,减少算法陷入局部最优的可能性。
2.3 WOA算法
鲸鱼优化算法(whale optimization algorithm,WOA)是由Mirjalili等于2016年提出的,属于一种群智能优化算法,算法的数学模型是以座头鲸的狩猎活动作为原型。鲸群的狩猎活动主要包含3种阶段:缩小包围圈、螺旋更新位置和随机搜索猎物[11]。鲸群中的每个个体代表着一个可能解,个体通过不断迭代更新在解空间中的位置,最终搜索到全局最优解。
2.3.1 包围阶段
在鲸群搜索猎物的过程中,如有鲸鱼发现猎物,鲸群整体会向猎物移动,实现包围。体现在算法模型中,数学表达式为:
X(t+1)=Xbest(t)-A·D
(12)
D=|C·Xbest(t)-X(t)|
(13)
式中:t为当前迭代次数;X(t+1)为个体更新后的位置;Xbest(t)为目前最优个体的位置。
系数A和C的表达式如下:
A=2a·r1-a
(14)
C=2·r2
(15)
式中:r1和r2为介于[0,1]之间的随机向量;a为一个收敛因子,随着迭代次数的增加从2至0线性衰减,标准WOA中一般定义为式(10)。
(16)
式中Tmax为最大迭代次数。
2.3.2 螺旋更新阶段
当座头鲸得到猎物的位置时,它的行为是绕着猎物以螺旋轨迹游动,不断接近目标,该过程的数学表达为:
D′=|Xbest-X(t)|
(17)
X(t+1)=D′·ebl·cos(2πl)+Xbest(t)
(18)
式中:b为常数,用于决定螺旋形状;l为[-1,1]间的随机数。
在WOA算法中,鲸鱼根据随机概率值选择包围和螺旋更新位置2种行为中的一种,假设2种行为的发生各有50%的概率,采用概率p来对鲸鱼位置更新所属阶段进行判断,具体表达式如下:
(19)
2.3.3 搜索阶段
当系数|A|≥1时,表示处于搜寻猎物的阶段,此时鲸群中的个体将通过随机运动的方式尝试获取猎物的方向,其数学表达如下:
D″=|C·Xrand(t)-X(t)|
(20)
X(t+1)=Xrand(t)-A·D″
(21)
式中Xrand(t)为从当前种群中随机选取的个体位置。
2.4 改进WOA算法(IWOA)
2.4.1 改进收敛因子a
在算法搜索初期,较大的a有利于快速对整个求解空间进行遍历,可以实现较强的全局搜索能力,从而能够确定最优解的大致范围。在逐渐接近最大迭代次数时,较小的a可以实现较强的局部搜索能力,这样才能使得后期寻优过程中不会错过最优解。
根据式(16)可知,a在标准WOA算法中为线性收敛。a的线性收敛不能平衡算法的全局和局部搜索能力,可能会致使算法易于陷入局部最优且效率低,进而影响算法搜索的精度。
对此,本文针对a提出一种非线性收敛方案,具体表达式如下:
(22)
2.4.2 引入自适应权重
在标准WOA算法中,最优解Xbest在式(19)中未得到充分利用[12]。本文引入自适应权重,利用最优解提升算法精度。
定义自适应权重系数ω如下:
(23)
同时,位置更新公式需做如下修改:
X(t+1)=ω(t)·Xbest(t)-A·D|A|<1,p<0.5
(24)
X(t+1)=D′·ebl·cos(2πl)+(1-ω(t))·Xbest(t)p≥0.5
(25)
在包围阶段的式(24)中,权重ω随着迭代次数的增加而增大,使得每次迭代后,个体会更加靠近猎物,从而提高算法的优化精度。在螺旋更新阶段的式(25)中,使用较小的权重,便于在更新位置的同时更好发现当前猎物周围的更优解,从而提升算法的局部搜索能力。
3 实验测试与结果分析
3.1 温度实验
神经网络模型的训练需要大量的加速度计温度实验数据,温度实验的环境对训练的结果尤为重要。本文构建了一个具有可重复性的温度实验系统,它由espec可编程温箱、高精度分度转台、QVBA样机、数据采集电路模块组成。安装时,QVBA的敏感轴垂直于转台平面,分度转台可以实现0°~360°的旋转,对QVBA实现-1g~+1g的加速度输入。
本文对QVBA样机进行多次重复性测试,温度测试范围为-40~60 ℃,以10 ℃为温度阶梯,共计11个温度点,每个温度点保温1 h。实验分为零偏数据获取和标度因数数据获取。在零偏数据获取中,加速度计处于0g状态,在每个温度点的保温阶段进行数据采集,采样频率为1 Hz。在标度因数数据获取中,每个温度点的保温阶段结束后,将加速度计分别置于+1g和-1g的状态下,待转台稳定后,每个位置至少记录1 min,采样频率为1 Hz。
在全温实验中,本文将补偿前后的加速度计输出进行对比,以全温零偏极差、全温零偏稳定性和全温标度因数稳定性作为评价指标。
全温零偏极差ΔBiasT的计算公式如下,单位为mg:
ΔBiasT=Biasmax-Biasmin
(26)
全温零偏稳定性Bstab的计算公式如下,单位为mg:
(27)
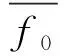
全温标度因数稳定性SFstab的计算公式如下,单位为ppm:
(28)

3.2 结果与分析
按照3.1中介绍的测试步骤,进行多次重复性温度实验。选取20 ℃作为模型温度的基准值,并对数据进行预处理。根据2.1中所述,结合实验条件,本文选择独立建模的温度补偿方案,得到补偿后的加速度输出为
(29)
式中:a(T)为补偿后的加速度;fout为加速度计实时输出频率。
获取当前温度,带入补偿模型可以得到该温度点下的零偏输出fBias(T)和标度因数SF(T)。
本文使用MATLAB R2023a对模型进行训练,其中IWOA的迭代次数设置为200次,种群数为30,零偏模型拟合后的均方根误差(RMSE)为0.014 5。
为证实模型的有效性,再次重复测试步骤,实现对验证数据的采集并带入补偿模型。根据验证数据的补偿结果,绘制出使用BP和IWOA-BP补偿前后加速度计零偏和标度因数随温度变化的折线图,分别如图3和图4所示。

图3 加速度计零偏补偿结果
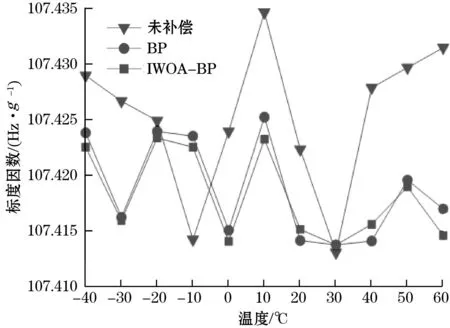
图4 加速度计标度因数补偿结果
图3和图4为QVBA在11个温度测试点下,使用BP模型和IWOA-BP模型补偿前后,加速度计的输出随温度的变化曲线。从图3、图4中可以看出,补偿前的加速度计输出明显受到温度的影响,产生了输出误差。经过IWOA-BP模型补偿后,加速度计的温度性能得到了一定的改善。验证数据集在补偿前后的标度因数和零偏参数的变化如表1所示。

表1 补偿前后加速度计性能参数对比
对比结果表明,与普通BP神经网络相比,经过IWOA优化的BP神经网络有着更好的准确性,普通BP神经网络由于自身的局限性,陷入了局部最优,未能得到全局最优解。经过IWOA-BP模型补偿后,全温实验下,零偏极差性能约提升了12倍,零偏稳定性性能约提升21倍,标度因数稳定性性能约提升40%,3项性能评价指标均得到了一定提升。
4 结束语
本文首先介绍了QVBA的工作原理,分析了温度误差产生原因,为了提高QVBA的温度性能,提出了一种基于IWOA的算法优化BP神经网络对QVBA的温度误差进行建模,改进后的算法提高了BP神经网络的鲁棒性和准确性。随后,对QVBA进行了温度实验,并利用采集的数据建立了温度补偿模型。经过补偿,全温零偏极差从12.241 mg下降至0.977 mg,全温零偏稳定性从4.161 mg下降至0.196 mg,零偏性能约提升1个数量级,全温标度因数稳定性从59.676 ppm下降至35.751 ppm。通过补偿前后数据对比,验证了提出的IWOA-BP温度补偿模型的有效性。

