一种基于凸优化的装备能力指标权重赋值方法

葛萌萌

(中国西南电子技术研究所,成都 610036)

0 引 言

装备能力评估可以全面了解装备的优点与不足,是装备建设中的重要一环。科学合理地评价装备能力可以反映装备在不同环境中的使用效果,进而辅助装备的开发论证以及多个备选方案的对比选择[1]。

指标权重赋值在装备能力评估中发挥着重要作用,直接影响着评估结果的合理性和准确性,因此一直是国内外学者关注的热点问题[2-3]。目前,指标权重赋值方法主要分为主观赋权、客观赋权和主客观相结合赋权3类方法。其中,主观赋权法主要是根据专家经验对各指标重要程度进行评价进而计算权重,如德尔菲法[4]、层次分析法[5]、环比评分法[6]等,但该类方法依赖专家经验,主观性太强;客观赋权法通过对指标数据进行分析,建立数学模型,进而实现指标的赋权,如灰色关联法[7]、标准间冲突性相关性法(Criteria Importance Through Intercriteria Correlation,CRITIC)[8]、熵权法[9]等,但该类方法完全忽视了专家经验和历史经验信息,可能会出现与实际情况不符合的问题。针对上述两类赋权方法的缺点,主客观相结合的赋权方法随之出现。文献[10]将属性层次模型法与CRITIC方法相结合,提高了权重配置的合理性。文献[11]将环比评分法与熵权法相结合,并利用优化模型将两种方法求得权重值集成起来。

熵权法作为一种经典的客观赋权法,主要是利用指标间的差异性来对指标进行客观赋权,但是该方法具有一定的缺陷,如在无人战斗机能力评估时,需要考虑侦察能力和打击能力两个评价指标,若在评估时打击能力表现出的差异性比侦察能力小,则不能片面地认为打击能力没有侦察能力重要。针对该问题,目前很多学者将信息熵与优化理论结合起来,通过指标间的灰关联深度系数来确定指标客观权重大小的变动范围,并利用极大熵准则构建优化模型,进而求解指标权重[12-13],但是该类方法中灰关联系数并不能真实反映指标的实际重要程度。

本文针对装备能力评估中指标权重配置问题,基于极大熵准则,提出了基于凸优化的装备能力指标权重赋值方法,通过案例分析验证了该方法的有效性及合理性。

1 评估指标体系设计

1.1 指标体系设计原则

评估指标是用来衡量装备效能优劣的标尺。装备能力不是一个可以直接测量得到的真实数值,需要通过一些具体的、能够量化的指标来反映,即装备能力评估指标体系。指标体系中选择的指标不能太少,否则将无法体现装备的各方面能力,同时也不宜太多,否则会造成指标体系过于庞杂、冗余,给后续评估工作造成困难。通常指标体系设计应该遵循以下原则[14]：

1)客观性——选取的各评估指标能够客观真实地反映装备能力;

2)完备性——指标体系能比较全面地反映被评估对象的方方面面,确保指标的完备性;

3)实用性——充分考虑所选取指标量化的难易程度和可靠性,使指标体系具备实用性;

4)科学性——影响装备能力的因素有很多,应分清主次,抓住主要因素,使评估指标体系既相对简单,又不影响装备能力评估的实质;

5)系统性——应按系统论观点,将指标体系作为一个有机的整体,分层次、分角度反映装备的能力。

1.2 指标体系构建流程

根据上述指标体系设计原则,在针对具体装备能力进行评估时,指标体系构建流程如图1所示。

图1 指标体系构建流程Fig.1 The flow chart of index system construction

评估对象及评估目的分析：评估对象、评估目的均会影响指标体系的构建,评估对象、评估目的不同,指标体系中所选择的具体指标也会不同,首先必须明确评估对象,对评估目的进行分析。

指标体系初建：根据评估对象和目的,构建评估指标初集,确定指标体系结构,初步建立指标体系。

指标体系筛选：初建的指标体系可能存在指标冗余、复杂等问题,因此需要进行检验筛选,保证指标精简、独立。

指标体系优化：通过专家咨询等方法,对筛选后的指标体系进行评价,判断是否科学完备,若是,即确定该指标体系为最终指标体系,否则根据专家意见进行指标体系优化。

1.3 机载雷达装备能力评估指标体系

依据上述设计原则与流程,以机载雷达装备能力评估为例,可以构建如图2所示的指标体系。由于机载雷达装备的主要作用是探测目标,在战场上探测目标的同时,也要考虑自身平台的生存能力和装备的可靠性,因此机载雷达装备能力指标体系以雷达探测能力、平台生存能力和装备可靠性3个指标作为二级能力,并基于机载雷达系统工作原理与结构,以最大探测距离、目标发现用时、定位误差、航迹连续性、机动速度、隐身系数、抗毁系数、平均故障间隔时间、无故障连续工作时间、平均故障修复时间作为底层能力指标。

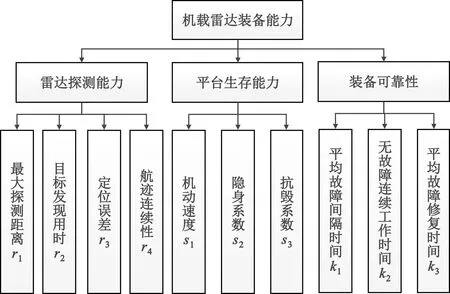
图2 机载雷达装备能力评估指标体系Fig.2 The capability evaluation index system for airborne radar equipment

2 基于先验信息辅助的指标权重赋值模型构建及求解

2.1 数据预处理

在进行指标权重赋值模型构建之前,需要对各底层性能指标数据进行预处理,使其规范在同一量纲下,也称归一化处理。

本文考虑的指标主要分为效益型和成本型,其中效益型指标归一化处理函数为[15]

(1)

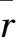
成本型指标归一化处理函数为

(2)

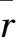
2.2 目标函数构建

由于各指标权重是一个随机变量,具有不确定性,而“熵”可以准确科学地反映指标的重要性分布程度。根据极大熵准则,在已知部分信息的基础上,认为所有指标的权重熵值总和达到最大时,指标权重的配置最为合理[13]。因此,可以构造如下目标函数：

(3)

式中：wi为第i个指标的权重;N为所求权重的指标个数。

2.3 约束条件确定

通常,一些先验信息可以作为约束条件。本节列举了一些在装备能力评估中常见的约束条件,分别进行描述。

1)显而易见,各指标权重之和为1,即

(4)

2)各指标权重均为非负实数,即

wi≥0,i=1,2,…,N

(5)

3)根据专家经验,某个指标对能力评估影响极大/极小,其权重值必须大于/小于某一数值,即

wp>χ或wp<χ,p∈{1,2,…,N}

(6)

4)根据仿真或试验验证,在相同指标体系下,装备1能力优于装备2能力,该先验信息也可作为约束条件,即

(7)

5)在某次试验中,对某装备进行了等级评估,该历史经验信息也可作为约束条件,即

(8)

2.4 模型构建及求解

根据上述目标函数以及约束条件,可以构建如下指标权重配置优化模型：

(9)

式中：hj(wi)为约束条件。可以有多个约束条件,由式(4)～(8)确定。

由于上述目标函数为凸函数,约束条件均为线性约束,因此,式(9)中的优化问题为凸优化问题,进而,权重wi(i=1,2,…,N)可以通过Matlab中CVX工具箱求解[16]。

3 案例分析

本节以1.3节建立的机载雷达装备能力评估指标体系中的雷达探测能力和平台生存能力两个二级指标为例,通过分别构建不同的优化模型,对两个二级指标的底层指标权重进行配置。

3.1 雷达探测能力

假设有3个型号的机载雷达装备,通过仿真/试验数据,可以先验已知其雷达探测能力排序为型号1>型号3>型号2,各底层指标数据如表1所示。

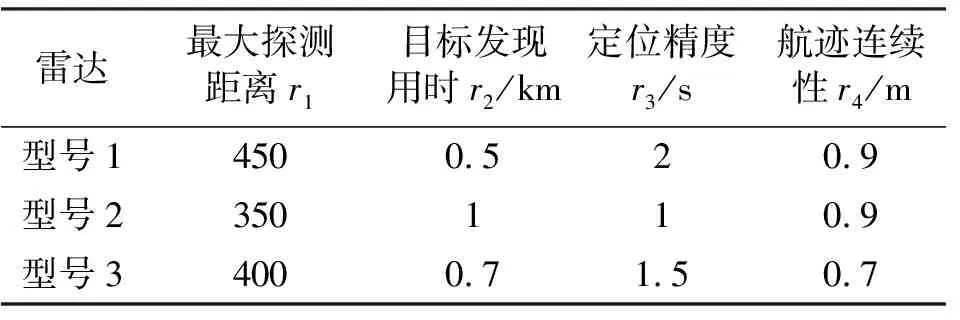
表1 各型号雷达探测能力底层指标数据Tab.1 The underlying index data of radar detection capability

在进行指标权重配置之前,首先对底层指标按式(1)和式(2)进行归一化处理,其中效益型指标有最大探测距离、航迹连续性;成本型指标有目标发现用时、定位误差。经过归一化处理后,其结果如表2所示。

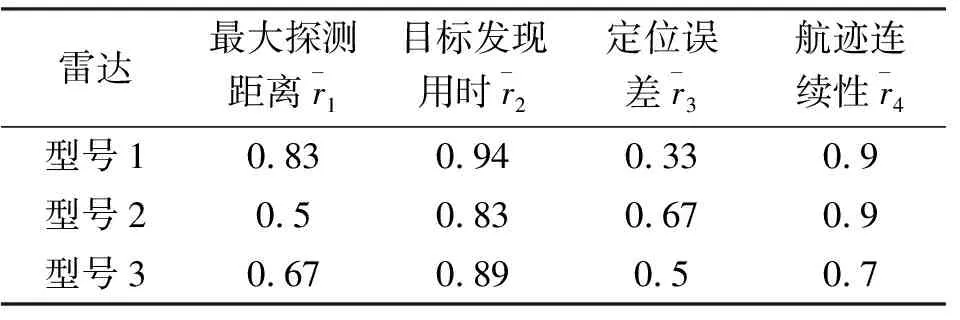
表2 各型号雷达探测能力指标数据归一化处理结果Tab.2 Normalization processing results of radar detection capability index data

进而,根据先验信息,可以构造如下关于权重配置的优化模型：

(10)

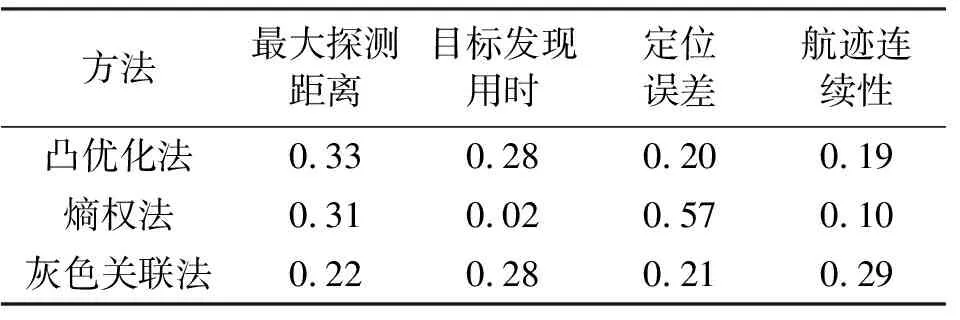
表3 各指标权重值Tab.3 The weights of radar detection capability index

从表3可以看出,各指标的权重各不相同,即各指标性能对雷达探测能力的影响程度也各不相同。根据本文提出的凸优化方法得到的各权重结果可以看出,定位误差和航迹连续性的权重较低,即定位误差和航迹连续性相对于其他指标对雷达探测能力影响较小。同时,从表2数据中可以发现,虽然各型号雷达探测能力为型号1>型号3>型号2,但是型号1的定位精度在各型号中反而最低,型号3的航迹连续性反而低于型号2,这也侧面反映了定位精度与航迹连续性两个指标对雷达探测能力影响较小,与求得的指标权重结果相符。而熵权法求得定位精度权重最大,灰色关联法求得航迹连续性权重最大,与实际不符,进一步表明凸优化方法更为准确、合理,更加贴合实际应用。

3.2 平台生存能力

针对平台生存能力,为方便计算,各底层指标归一化后的数据如表4所示。

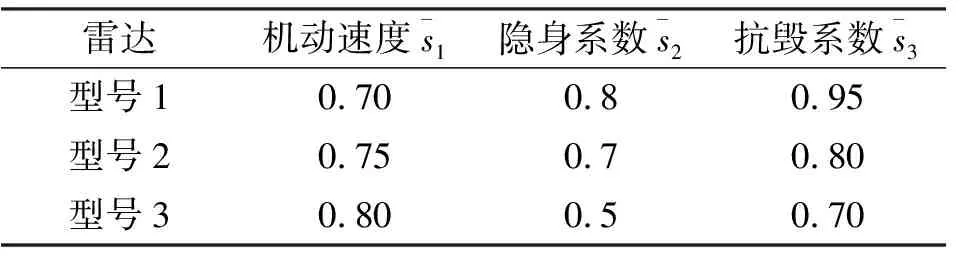
表4 各型号平台生存能力底层指标量化值Tab.4 The quantified values of the underlying index for platform survivability

假设专家认为隐身系数对平台生存能力影响很大,其权重不小于0.5,同时,假设3个型号的平台生存能力按五等级标度法进行等级评价,分别为很好、好、一般。以此先验信息为约束条件,可以构造如下优化问题：

(11)

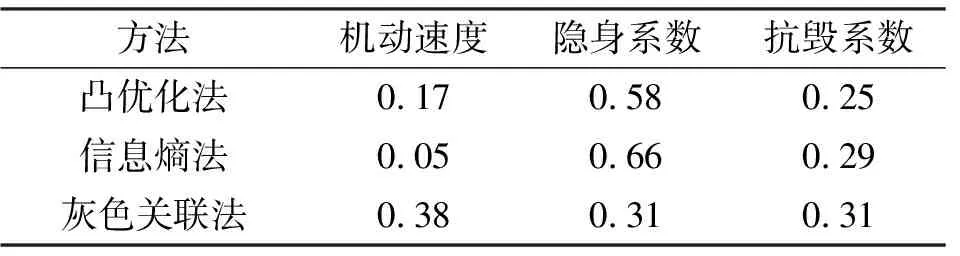
表5 各指标权重值Tab.5 Weights of the platform survivability index

根据表4和表5可以看出,由于型号1的机动速度<型号2<型号3,但是型号1的平台生存能力却大于型号2和型号3,因此可以判断机动速度指标对平台生存能力影响较小,其指标权重也应该较小。利用本文提出的方法得到的机动速度的指标权重为0.17,在3个权重值中最小,与实际相符。求得的权重结果均满足约束条件,表明了该算法的有效性。同样地,指标权重配置的合理性优于熵权法和灰色关联法。

4 结 论

本文针对装备能力评估中指标权重配置问题,基于极大熵准则,提出了基于凸优化的装备能力指标权重赋值方法。首先,构建了机载雷达装备能力评估指标体系;然后,以最大化各指标权重的熵值总和作为目标函数,常见的先验信息作为约束条件,构建指标权重配置优化模型,并利用CVX工具箱求解指标权重;最后,以机载雷达装备能力评估指标体系为例,验证了该方法的有效性,并与熵权法和灰色关联法作对比,进一步说明了该方法更为准确、合理,贴合实际应用。