利用无监督预训练的轨迹深度关联

李 平,李雨航

(中国西南电子技术研究所,成都 610036)

0 引 言

在空、海战场监视系统的常规性执勤任务中,由于雷达探测结果存在系统性误差[1],使得同一真实目标会产生多条空间位置平行或相交的轨迹。轨迹关联是将此类误差轨迹判断为一个目标,对于监视分析任务尤为重要。

轨迹关联一般基于时空相似度算法结合聚类的方式,核心在于使用高度量性的相似度算法。文献[2]利用最长公共子序列度量轨迹的相似度,并通过具有噪声的基于密度的聚类(Density-based Spatial Clustering of Applications with Noise,DBSCAN)算法对出租车轨迹进行聚类。文献[3]通过计算子轨迹间的水平距离、垂直距离、角度距离来度量轨迹的相似性,并提出轨迹空间聚类(Trajectory Ordering Points to Identify the Clustering Structure,TR-OPTICS)算法用于轨迹聚类。这些方法对噪声具有较强的鲁棒性,但仅考虑轨迹点序列的空间位置来衡量相似度,没有从时间维度进行度量,导致准确度不高。文献[4]结合时空属性提出时间加权相似度(Time Weighted Similarity,TWS)和空间加权相似度(Space Weighted Similarity,SWS)有效提升轨迹相似度的准确性。该方法通过调整相似度和距离等阈值参数能够高效地处理实时轨迹关联,但其准确性受参数设置的影响较大,迁移性弱,且忽略了轨迹内部各点的关联性以及轨迹的形状特征。

随着深度学习的发展,通过构建神经网络模型,自动提取数据深度特征,在信号处理、自然语言处理等领域都得到了广泛的应用。文献[5]使用长短时记忆(Long Short-Term Memory,LSTM)神经网络提取干扰信号的时域、频域特征,完成特征融合后进行分类识别。文献[6]利用循环神经网络(Recurrent Neural Network,RNN)模型对人员轨迹进行分类,并设计多种检测评估方式对人员位置进行估计。文献[7]通过构建双向注意力机制模型,设计遮蔽语言模型(Masked Language Model,MLM)与下句预测(Next Sentence Prediction,NSP)相结合的预训练任务,以无监督的方式训练出高精度的预训练模型。文献[8]通过增加训练数据扩大向量编码长度,并仅使用遮蔽语言模型设计预训练任务,训练得到更鲁棒的预训练模型。文献[9]通过构建更简洁的词嵌入层大幅度减少模型参数量,并设计更具学习难度的序列顺序预测任务(Sentence Order Prediction,SOP),使模型在维持原有性能的前提下参数量大幅减小。利用大量无标注领域数据以无监督方式作预训练,使用少量标注数据对预训练模型参数进行微调成为当今的主流解决方案。然而,在轨迹关联领域,基于深度学习的预训练模型应用较少。

针对时空相似度算法参数敏感迁移性差的问题,本文采用深度学习方法,提出一种基于无监督预训练的轨迹自动关联方法。利用Geohash经纬度编码算法表征轨迹特征,构造双向自注意力机制神经网络结构对无标注轨迹数据进行预训练;构建孪生网络结构训练少量标注轨迹对,得到高度量性能的轨迹匹配模型。采用Geolife GPS轨迹数据集[16-18]进行模型验证,结果表明,基于深度学习预训练的轨迹自动关联效果在轨迹关联领域达到最优。

1 轨迹数据预处理

1.1 轨迹数据去噪

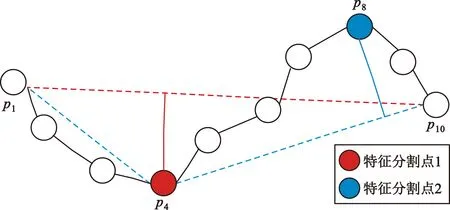
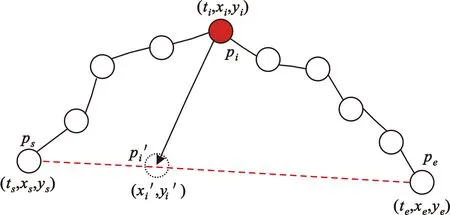
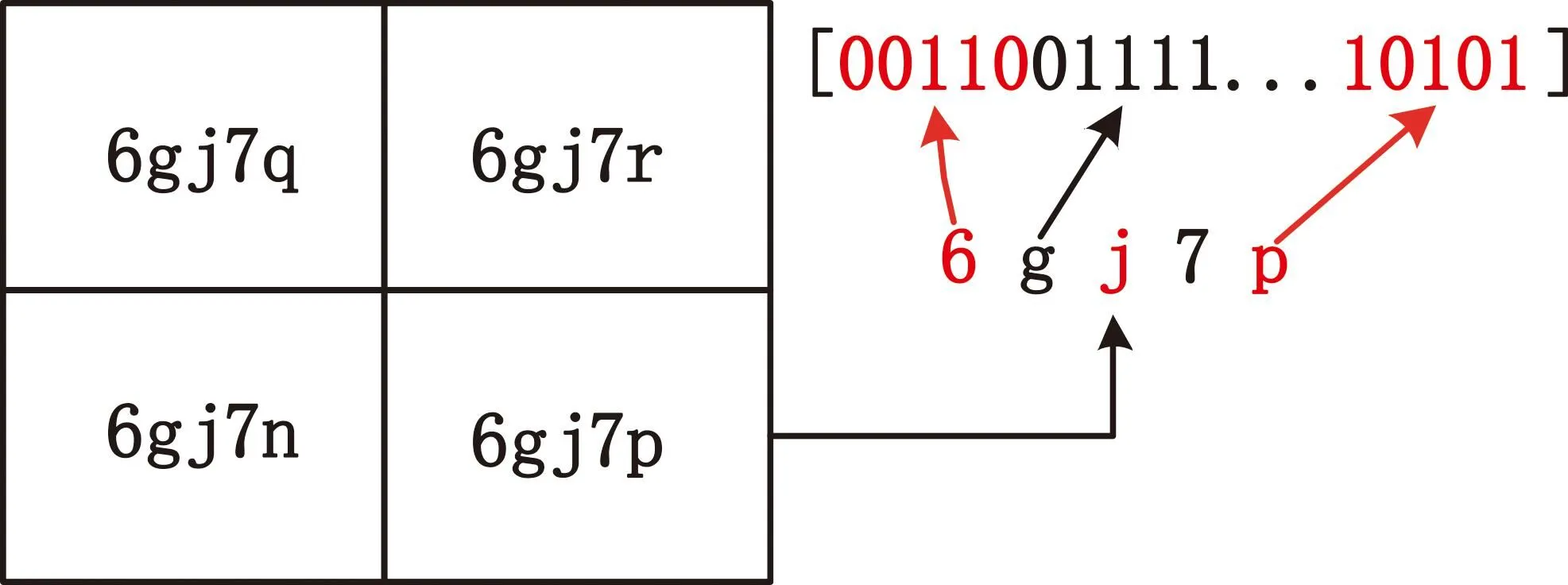
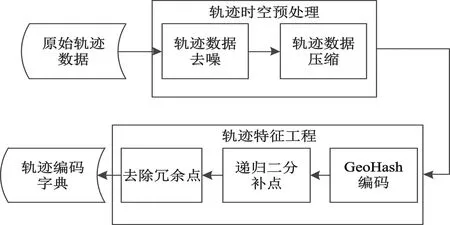
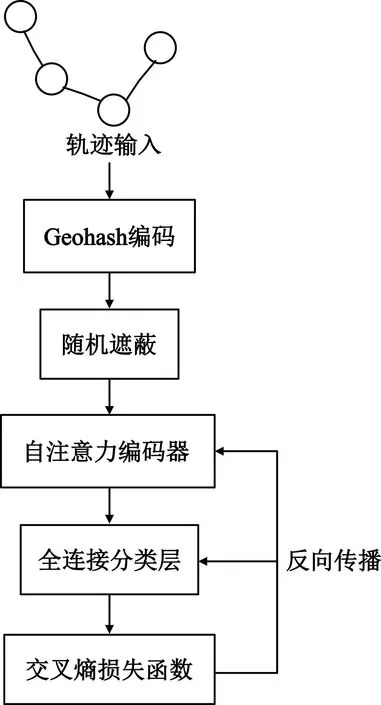
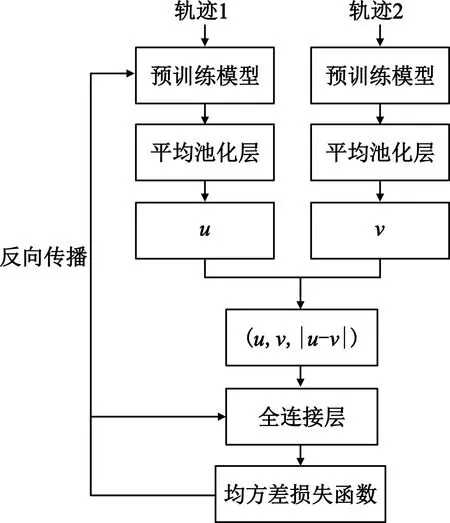
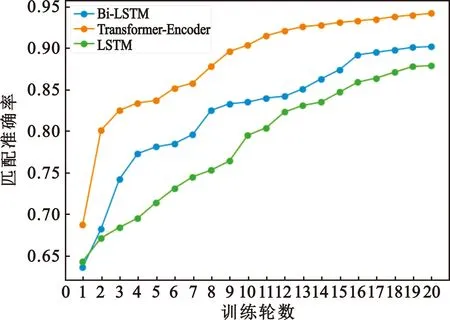
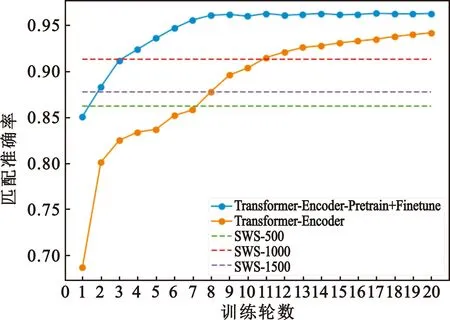
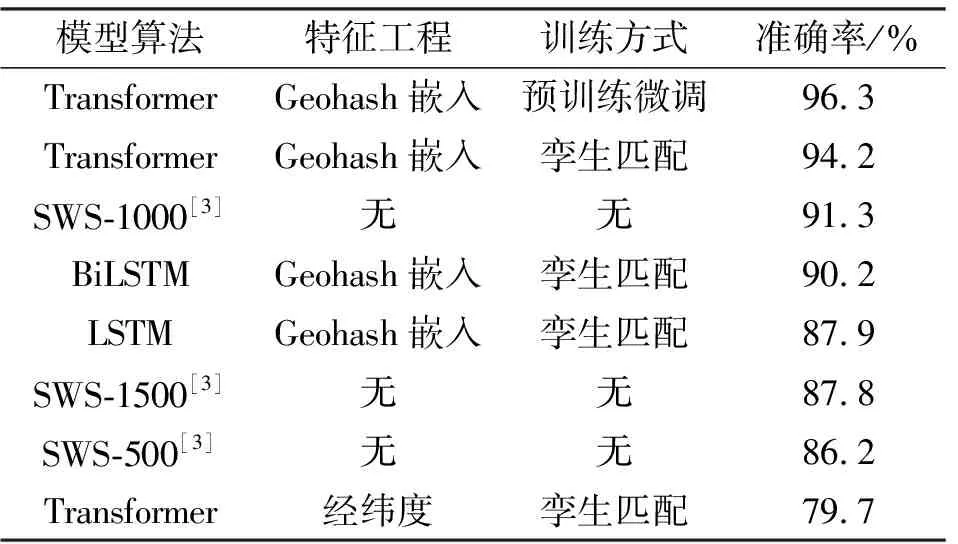
传感器捕获的轨迹数据可表示为T=[(p1,t1),(p2,t2),…,(pn,tn)],其中(pi,ti)表示在ti时刻(t1

(1)

式中：pk表示轨迹中的第k个点;l为滑窗窗长。当处理第k个点时,将该点与其前l-1个点一起求平均得到滤波后的点。从轨迹起始点开始,以步长为1进行滑窗,依次处理各点得到去噪后轨迹。

1.2 轨迹数据压缩

轨迹压缩能够大幅度去除冗余轨迹点,保留关键轨迹信息,减小轨迹处理计算量,并提升轨迹数据处理的鲁棒性。Douglas-Peucker算法[11]被广泛使用于轨迹数据压缩中,轨迹压缩过程如图1所示。

图1 轨迹压缩过程Fig.1 The process of trajectory compression

轨迹序列的起始点被选作锚点,结束点被选作浮动点。计算两点之间所有轨迹点到其连线的垂直距离,筛选出其中的最大值,如最大值超过设置的距离阈值,该最大值点被认定为特征分割点并储存。从特征分割点处将轨迹分为两段,将前段的特征分割点设置为浮动点,后段的特征分割点设置为锚点。对每段子轨迹都进行上述步骤的递归操作,直到所有距离都小于阈值。存储的所有特征分割点以及原始始末点所构成的轨迹按照时序排列,即为压缩后的轨迹。该算法只考虑了轨迹空间关系,忽略了时间因素的影响。时间比率算法(Top-Down Time-Ratio Algorithm,TD-TR)[12]将考虑时间因素的距离计算方式加入Douglas-Peucker算法中,计算时间相对距离的方式如图2所示。

图2 时间相对距离Fig.2 The relative distance of time

(2)

1.3 Geohash轨迹预处理

轨迹序列一般基于轨迹点的经纬度表征为二维向量形式,该方式所能表示的信息量较少。针对神经网络模型的特征提取,本文的轨迹高维向量转化方法分为两步：首先基于Geohash编码将轨迹点编码为字符串并构成编码字典;其次随机初始化编码向量映射矩阵,完成轨迹的向量转化。

如图3所示,Geohash编码基于Base32编码通过递归二分的方式将二维经纬度转化成字符串,每一个字符串代表某一空间区域,编码位数越多区域越小,定位更精准,矩形区域中的所有坐标点都共享该字符串[14]。

图3 Geohash编码示例Fig.3 Example of Geohash encoding

对轨迹数据编码并构造编码字典,再随机初始化Geohash向量嵌入矩阵,利用向量嵌入将轨迹序列映射至高维向量空间。轨迹序列由二维经纬度离散向量转化为高维连续区域栅格编码向量,使得模型更容易学习到轨迹内部以及轨迹之间的关系表示。本文对输入轨迹完整预处理方式如图4所示。

图4 轨迹预处理流程Fig.4 The pre-processing flow of trajectory

原始轨迹数据依次通过均值滤波器剔除轨迹噪声点,通过TD-TR算法压缩轨迹,完成轨迹时空预处理。其次,对压缩后轨迹数据做特征工程处理,利用Geohash编码得到轨迹中所有点的编码表示;构建窗长为2、步长为1的滑窗,按照时间顺序从起始点开始对轨迹数据进行滑窗操作,当滑窗内两轨迹点对应的Geohash编码不一致时,使用递归二分补点方式在两轨迹点之间补点并按照时间顺序排列,直到新增点对应的Geohash编码与其邻接点保持一致;依次遍历补点后的轨迹数据去除邻接点中Geohash编码重复的点。最后,整理全部轨迹点的Geohash编码去重并保存为编码字典。上述方式能够丰富原始轨迹数据特征,减弱不同物理设备采样率、精度不同所造成的数据失真,并且将二维轨迹点数据转化为契合神经网络模型的输入形式。

2 模型构建与训练

2.1 自注意力机制神经网络模型构建

自注意力机制神经网络模型(Transformer)[7]通过引入自注意力机制,接收一个向量序列并产生一个重新加权的向量序列,在机器翻译领域取得了重大突破。本文基于Transformer的编码器结构构建基于自注意力机制的特征提取结构,提取轨迹数据深度特征。优化后的神经网络模型结构如图5所示。

图5 自注意力编码器结构Fig.5 Self-attention encoder structure

首先,原始输入轨迹信号通过序列嵌入层映射为高维向量输入,通过线性尺寸调节层减小向量尺寸,降低模型计算复杂度。其次,依次通过查询线性转换层、键线性转换层、值线性转换层得到查询矩阵、键矩阵、值矩阵,利用查询矩阵与键矩阵求得注意力分数矩阵。可用下式来表示注意力分数的计算过程：

(3)

式中：Q表示查询矩阵;K表示键矩阵;dk表示向量隐藏层大小;softmax()为激活函数,可表示为

(4)

2.2 基于遮蔽预测的轨迹预训练

基于大规模数据量的无监督预训练任务,在自然语言处理领域能大幅度提升各类下游任务的性能[7-9]。本文对无标注轨迹数据进行预训练,提升模型对轨迹深度特征提取能力。预训练过程如图6所示。

图6 预训练过程Fig.6 Pre-training process

原始轨迹数据通过Geohash编码转化为编码序列;对编码序列进行随机遮蔽操作,随机选中编码序列中15%的部分,对选中的编码以80%的概率替换为字符MASK,10%的概率保留,10%的概率替换为字典中任意一个编码[8];将遮蔽后的编码序列通过自注意力编码器得到考虑编码序列各部分重要性的加权输出;通过全连接分类层得到每一个编码位置对应的预测结果;将MASK编码对应的预测结果输入至交叉熵损失函数计算损失值。交叉熵损失函数可表示为

(5)

式中：y是样本x属于某一个类别的真实概率;fθ(x)是神经网络结构输出的样本属于某一类别的预测分数。损失值L用来衡量预测结果与真实结果的差异性。最后,利用Adam优化器更新自注意力编码器以及全连接分类层的模型参数。重复以上过程,完成模型预训练,提升对轨迹数据的向量编码能力。

2.3 孪生匹配网络结构

构造带标签的轨迹对匹配数据集,基于孪生网络结构[13],构建孪生匹配神经网络;通过训练轨迹对匹配任务,对预训练后的自注意力模型进行参数微调。孪生匹配神经网络结构如图7所示。

图7 孪生匹配网络结构Fig.7 Siamese matching network structure

轨迹对数据依次通过预训练后的自注意力模型输出重新加权求和后的轨迹点高维向量集合;利用平均池化层,从轨迹点的维度对向量求平均,降低向量尺寸,分别得到两轨迹的向量表示u,v;将两轨迹向量以及两者的绝对偏差向量|u-v|横向拼接得到轨迹对向量;通过全连接层输出轨迹对相似值,进一步利用均方差损失函数求得训练损失值,该过程可表示为

(6)

式中：y是样本x属于某一类别的真实概率;fθ(x)是神经网络结构输出的样本属于某一类别的预测分数。最后,在反向传播过程中更新自注意力模型与全连接分类器的参数。重复以上过程,完成孪生匹配网络结构参数微调,使模型能够输出轨迹对信号的相似度分数。

3 实验结果

为了评估特征工程方式、神经网络结构、预训练方式对轨迹信号匹配能力的影响以及与时空相似度算法相比深度学习的有效性,本文根据轨迹深度关联的流程进行以下3组实验：

实验1,利用Geohash向量嵌入与直接使用经纬度完成特征工程进行轨迹匹配;

实验2,分别构造自注意力神经网络结构(Transformer)、长短时记忆(LSTM)神经网络、双向长短时记忆(Bidirectional LSTM,Bi-LSTM)神经网络作为特征提取器进行轨迹匹配;

实验3,引入预训练方式与直接使用标注轨迹对数据集训练,以及使用实时场景表现优秀的空间加权相似度(Space Weighted Similarity,SWS)算法[3]进行轨迹匹配。

实验数据集采用微软亚洲研究院公开的用户生活轨迹GPS数据集(Geolife)[16-18]。该数据集采集了182位用户为期5年的生活轨迹,共计17 621条轨迹,涵盖了中国30个城市,出行方式包括步行、慢跑、自行车、公交车、自驾、火车、飞机。数据的采集使用多种GPS记录设备,平均采样率为1～5 s或者5～10 m,轨迹点信息包含经度、纬度。为构造匹配轨迹集,从原始数据集中任意选取1 000条轨迹,依次对轨迹数据进行采样间隔为2,4,6,8点的重采样。为增强数据鲁棒性,将信噪比设置为50 dB构造经度、纬度的高斯白噪声添加至轨迹数据。以5%的概率任意选取轨迹点并以5 000～10 000 m的距离偏差构造异常点。经过上述处理后,每条原始轨迹构造得到4条关联轨迹,共计5 000条关联轨迹集。将匹配的轨迹数据两两组合得到10 000对正样本轨迹对,同时筛选时间与空间距离较为接近的负样本对,构造得到10 000对负样本轨迹对,共计20 000对关联轨迹对数据,正负样本对比例为1∶1,按照9∶1的比例划分为训练集与测试集。

在神经网络训练方面,使用Python语言和Pytorch深度学习框架,学习率设置为2×10-5,batchsize设置为40,epoch设置为20。

3.1 两类特征工程方式的轨迹对匹配准确率

构造自注意力机制模型用于训练与测试,隐藏层向量尺寸设置为128,隐藏层深度设置为4,多头注意力数目设置为32。采用Geohash向量嵌入方式时,编码字典基于Geolife原始17 621条轨迹数据集构造,嵌入向量尺寸设置为32。上述参数为实验过程的最优设置。通过线性层将嵌入向量尺度转化为隐藏层向量尺度;采用经纬度构造方式时,将经纬度直接作为向量输入,通过线性层将其向量尺度调节为与隐藏层相同。测试准确率随训练迭代轮数的变化情况如图8所示。

图8 匹配准确率变化曲线(实验1)Fig.8 Matching accuracy in Experiment 1

使用Geohash向量嵌入方式在2 000轨迹对测试集上达到94.2%的匹配准确率相较于直接使用经纬度作为向量输入提升14个百分点。5位的Geohash编码每一个编码栅格大约能够表示10 km2,即大致5 100万个编码就能表征整个地球,与之相比4位精度的经纬度则需要约648亿个组合,实际情况会更加稀疏,使得模型的训练难度大幅度提升,因此Geohash向量嵌入方式更有利于模型学习轨迹点之间的关联关系。

3.2 3类神经网络结构作为特征提取的轨迹对匹配准确率

基于Geohash向量嵌入完成特征工程,分别构建自注意力神经网络结构、长短时记忆神经网络、双向长短时记忆神经网络作为特征提取器,隐藏层向量尺寸都设置为128,隐藏层深度都设置为4,自注意力神经网络结构的多头注意力数目设置为32。测试准确率随训练迭代轮数的变化情况如图9所示。

图9 匹配准确率变化曲线(实验2)Fig.9 Matching accuracy in Experiment 2

自注意力神经网络结构(Transformer)、双向长短时记忆神经网络(Bi-LSTM)、长短时记忆神经网络(LSTM)在2 000轨迹对测试集上的匹配准确率分别为94.2%,90.4%,87.9%。LSTM为单向的循环神经网络编码器,仅考虑了前序序列对后序序列的影响;Bi-LSTM基于前向LSTM与后向LSTM拼接而成,考虑了上下文序列的影响,但是对长距离的影响关系存在遗忘性;Transformer引入自注意力机制,考虑上下文序列的影响,基于注意力矩阵度量不同位置序列之间的影响关系,不会因为距离因素产生遗忘,因此,Transformer编码器更适合对轨迹序列的特征编码。

3.3 两类训练方式和SWS算法的航迹对匹配准确率

基于Geohash向量嵌入完成特征工程构造自注意力机制模型,隐藏层向量尺寸设置为128,隐藏层深度设为4,多头注意力数目设置为32。基于Geolife原始17 621条轨迹数据集作预训练,并基于18 000对匹配轨迹对训练集对预训练后的模型进行参数微调;SWS算法距离阈值分别设置为500 m,1 000 m,1 500 m。基于2 000对匹配轨迹对测试集进行测试,测试准确率随训练迭代轮数的变化情况如图10所示。

图10 匹配准确率变化曲线(实验3)Fig.10 Matching accuracy in Experiment 3

SWS算法在距离阈值设置为1 000 m时性能最佳。预训练结合参数微调的方式比直接使用标注轨迹训练匹配准确率提升2个百分点,比SWS-1000算法匹配准确率率提升5个百分点。SWS算法具有较为优异的基线能力,但其对距离阈值的设置较为敏感,泛用能力较弱。随机掩码预训练任务同样适用于轨迹序列,此任务为无监督不需要人工整理训练数据集,可以提供大数据量的轨迹数据作为预训练数据集,使得模型更好地学习轨迹数据的特征分布,预训练后的模型加强了下游轨迹匹配的模型基准能力。

3组实验综合匹配准确率如表1所示。从本文实验数据可以看出,从特征工程的角度比较,使用Geohash向量嵌入方式提升模型匹配性能14个百分点,向量嵌入的特征工程方式更能表示轨迹数据的特征结构;从模型结构的角度比较,Bi-LSTM比LSTM的匹配性能高2个百分点,Transformer相较Bi-LSTM匹配性能提升4个百分点,自注意力机制的注意力加权求和方式更能提取关键特征信息;从训练方式的角度比较,预训练参数微调方式,相比直接训练匹配模型,模型的收敛速度更快,并提升匹配性能2个百分点,预训练方式增强神经网络结构对轨迹数据的特征表示能力;从算法层面比较,预训练微调方式相较SWS算法提升5个百分点匹配准确率,时空相似度算法根据不同的轨迹点分布情况需调节合适的距离阈值,本文提出的Geohash向量嵌入结合预训练微调的方式更具鲁棒性,且轨迹关联性能更高,取得了最优实验结果。

表1 模型匹配准确率Tab.1 Model matching accuracy

4 结束语

本文针对轨迹匹配问题提出了一种基于无监督预训练的轨迹深度匹配关联方法。采用公开数据集进行的实验结果表明,Geohash向量嵌入结合自注意力神经网络结构使用预训练微调的方式,轨迹匹配准确率高于时空相似度度量方式,可达96.3%,说明该方式能提取轨迹数据的深度特征,提高轨迹匹配精度。

从本文实验可以看出,特征工程轨迹向量处理方式、模型特征提取方式以及预训练任务会影响模型的匹配性能,这为以后的研究提供了思路,具备工程应用推广性。后续研究工作主要从三个方面展开：第一,将轨迹信号可能含有的其他特征,如高度、速度、方向、意图等融入向量嵌入的表达方式中,丰富特征结构,提高输入模型的特征向量质量;第二,对预训练任务进一步研究,设计与特征相关的预训练任务与随机掩码任务相结合,提升模型对轨迹数据的特征表示能力;第三,针对模型复杂度与训练耗时的问题,研究在提升准确率的同时通过调节模型结构、向量嵌入等方式降低模型训练复杂度。结合以上研究内容,将继续开展其他类型轨迹数据集及模拟实时轨迹的实验验证。