工程预算在建筑工程造价控制中的应用研究
张晓辉
(中铁十二局集团建筑安装工程有限公司,山西 太原 030000)
建筑工程造价控制是整个工程建设过程中极为关键的一环,它涉及到项目的投资决策、设计、施工以及竣工验收等各个阶段。而工程预算作为工程造价控制的核心,对于合理确定工程造价、有效控制工程投资、提高企业经济效益等方面都具有重要意义[1]。
工程预算是指在工程建设过程中,根据工程设计、施工图纸、定额标准、取费标准等,对工程所需资金进行预先计算和确定的过程。它不仅是工程建设的基础,也是工程造价控制的重要依据。通过工程预算,可以合理确定工程的投资规模、资金使用计划,为项目的决策和实施提供有力支持。
1 建筑工程造价原始数据列的修正与预处理
工程预算的关键环节是人员消耗量、材料消耗量和机械消耗量的确定。因此,本文提出采用实地调查法、定时测量法和访问调查法三种方法来收集建筑工程造价原始数据。通过对上述方法的综合应用,不仅可以明确当前建筑业所使用的施工工艺和技术手段,而且可以确保所测数据的代表性[2]。此外,通过对施工各方的采访、调查,可以确保定额子目的合理和完整。
原始数据的预处理可理解为对异常数据的处理。可采用误差极限调整的方法将异常数据剔除。在剔除前需要确定观测次数[3]。在实际要求的精确度条件下,数据序列的分布性系数为:
式中:Kp代表数据序列的分布性系数;tmax代表有效数据最大值;tmin代表有效数据最小值。精确度可以通过下述公式确定:
式中:E代表精确度;代表算数平均值;vi代表残余误差;n代表观测次数。
在上述公式当中,若Kp的值与1越接近,则说明数据差异稳定范围越小,数据可利用价值越高,越不需要通过增加测定次数的方式获得更多数据。若Kp的值与0越接近,则说明数据差异稳定范围越大,数据可利用价值越低,越需要通过增加测定次数的方式获得更多数据。利用误差调整法对上述处理的数据序列进行修正。表1为误差调整系数对照表。

表1 误差调整系数对照表
将得到的调整系数代入到下述公式中,确定数据序列的最大极限值和最小极限值,进一步确定建筑工程造价原始数据的标准范围:
式中:Limmax代表建筑工程造价原始数据最大极限值;Limmin代表建筑工程造价原始数据最小极限值;K代表调整系数。在上述处理过程中,为进一步提高数据质量,可结合改进格鲁布斯原则对异常值进行分析和剔除,其流程如图1所示。
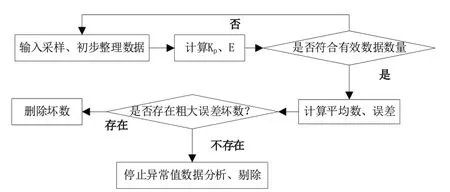
图1 改进格鲁布斯原则对异常值进行分析和剔除流程图
按照上述论述,收集建筑工程造价的原始数据。这些数据可能包括人工成本、材料成本、设备成本、间接费用等。对收集到的数据进行清洗,去除重复、错误或不完整的数据。使用格鲁布斯原则或其他相关方法对数据进行异常值识别[4]。异常值是指那些明显偏离其他数据点的值,可能由于错误、异常操作或其他原因导致。对识别出的异常值进行深入分析,了解其产生的原因。这可能包括检查数据来源、核对计算过程等。根据异常值的分析结果,决定是否剔除这些异常值。如果异常值是由错误或异常操作导致的,可以考虑剔除;但如果异常值是由正常范围内的波动或其他合理原因导致的,可以保留[5]。剔除异常值后,对剩余数据进行重新计算,以得到更准确、可靠的建筑工程造价数据。通过以上流程,可以改进格鲁布斯原则在建筑工程造价原始数据列中异常值的分析和剔除过程,提高数据的准确性和可靠性,为建筑工程造价控制提供更准确的数据支持。
2 构建工程预算定额调整模型
结合灰色理论模糊计算,构建工程预算定额调整模型。首先,需要确定工程预算定额调整模型的输入和输出变量。输入变量可能包括建筑工程的各个分项工程的造价数据、市场价格波动、政策变化等因素。输出变量可能包括调整后的工程预算定额。利用灰色理论,建立灰色预测模型。灰色预测模型可以对含有不完全信息的数据序列进行预测,具有计算简单、运算量小、精度高、可靠性高等优点。模型的基本形式为:
式中:x(0)代表原始数据序列;x(0)(k+1)代表预测值;a和b均为模型参数。该模型可以通过最小二乘法求解。
在灰色预测模型的基础上,结合模糊数学理论,建立模糊数学模型。模糊数学模型可以对具有模糊性、不确定性或不完全确定性的问题进行处理,提供更加灵活、全面的解决方案。图2为模型的基本运算程序。
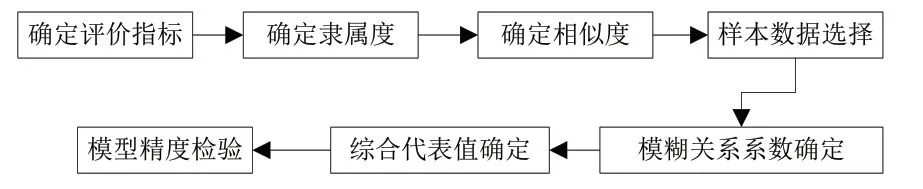
图2 模型运算程序图
根据输入变量的特征和实际情况,确定每个输入变量的隶属度函数。隶属度函数用于描述输入变量对输出变量的影响程度,可以根据具体情况进行调整和优化[6]。利用模糊数学模型和隶属度函数,对输入变量进行模糊运算。通过模糊运算,可以得到输出变量的模糊值。根据输出变量的模糊值,确定调整系数。调整系数用于对工程预算定额进行调整,可以根据实际情况进行调整和优化。利用调整系数,对工程预算定额进行调整,得到调整后的工程预算定额。
3 串行设计模式下的工程总价控制
工程预算在建筑工程造价控制中的应用中,串行设计模式下的工程总价控制是一种重要的策略。在串行设计模式下,工程总价控制首先需要将整个工程的预算进行分解,细化到个别的项目或工作包。通过这种方法,可以使预算更具操作性、可控性,并方便对其进行监测与调整[7]。图3为串行设计模式下的建筑工程造价控制流程图。

图3 串行设计模式下的建筑工程造价控制流程图
串行设计模式强调工程的阶段性,每个阶段都有相应的设计、施工和验收等环节。在每个阶段开始时,根据该阶段的工作内容和目标,制定相应的预算。随着工程的推进,对每个阶段的实际成本进行跟踪和监控,确保不超出该阶段的预算。
在串行设计模式下,由于设计阶段和施工阶段是顺序进行的,因此,在设计阶段就可以根据预算情况进行相应的优化和调整。例如,在设计阶段可以通过价值工程分析等方法,对设计方案进行优化,以降低成本或提高性价比。在施工阶段,也可以根据实际情况对预算进行调整,例如,对材料采购、人工费用等进行重新评估和预算。在串行设计模式下,由于设计和施工的顺序性,一些潜在的风险可能在后续阶段才会显现。因此,在工程总价控制中需要加强对风险的识别和应对[8]。例如,在设计阶段就需要考虑施工阶段的潜在风险,并制定相应的应对措施和预算调整方案。在串行设计模式下,工程总价控制还需要建立一个有效的信息反馈机制。通过对每个阶段的实际成本和预算执行情况进行分析和比较,可以及时发现问题和不足,为后续阶段的预算制定和调整提供经验和参考。同时,也可以通过持续改进和优化预算控制方法和技术,提高工程造价控制的效率和准确性。最终,按照图4所示,将通过串行设计得到的成果发布。
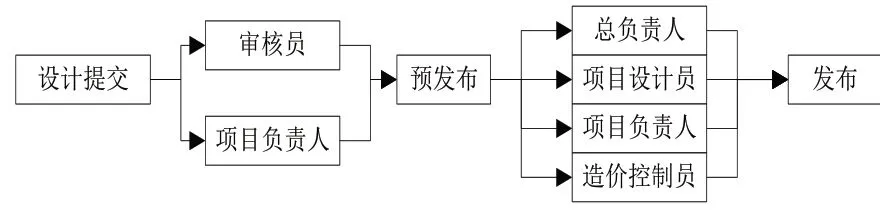
图4 串行设计成果发布示意图
总之,工程预算在建筑工程造价控制中的应用中,串行设计模式下的工程总价控制是一种全面、系统和动态的管理策略。它强调对整个工程造价过程的全面监控和调整,确保工程造价在可控范围内并实现最佳的经济效益。
4 应用实例
以某办公楼建筑工程项目为例,对其进行造价控制。该办公楼为框架结构,局部地下1层、地上4层、首层为4.3 m,标准层为3.8 m,总建筑面积为5 863.25 m2。本项目拟采用一根15 m长的预应力混凝土方桩桩基,单桩极限承载力为850 kN。静压沉桩时,按标高控制和受压桩力控制,以控制压桩力为主要依据,以设计标高为参照。挡水板、承台梁的混凝土标号为C30,抗渗等级为P6。
选择将该工程中叠合梁施工环节产生的造价作为研究对象,将利用工程预算的工程造价控制结果与该项目设计阶段给出的造价标准记录如表2所示。

表2 控制结果与标准对照表
结合表2中的内容,我们可以对工程预算在建筑工程造价控制中的应用效果进行分析。从表2中的数据可以看出,在各个项目中,控制结果的造价均低于设计阶段要求的造价标准。这意味着通过有效的工程预算控制,建筑工程的造价得到了有效的管理和控制。
首先,工程预算在建筑工程造价控制中的应用有助于提高工程造价的准确性。通过精确的预算编制和严格的预算执行,可以减少不必要的浪费和支出,确保工程造价在可控范围内。
其次,工程预算在建筑工程造价控制中的应用有助于提高工程的效益。通过有效的预算控制,可以确保工程建设所需的资金得到合理分配和使用,避免资金浪费和挪用。这有助于提高工程的效益和投资回报率。
最后,工程预算在建筑工程造价控制中的应用还有助于提高工程的透明度和可追溯性。通过详细的预算记录和监控,可以确保工程的各项支出和收入都有明确的记录和来源,便于后续的审计和检查。
综上所述,从表2中的数据可以看出,工程预算在建筑工程造价控制中的应用是可行的。通过有效的预算编制和执行,可以确保工程造价得到有效控制,提高工程的效益和透明度。因此,我们应该继续加强工程预算在建筑工程造价控制中的应用,提高工程造价管理的效率和准确性。
5 结语
总之,工程预算在建筑工程造价控制中具有重要作用。在实际应用中,通过加强人才培养、完善预算编制制度、加强施工过程中的费用控制以及引入先进技术和管理方法等措施,可以提高工程预算在建筑工程造价控制中的应用效果,为项目的决策和实施提供有力支持。

