NTRU 格上高效紧凑密钥封装方案

梁志闯 郑婕妤 赵运磊,2

1（复旦大学计算机科学技术学院 上海 200433）

2（密码科学技术国家重点实验室 北京 100036）

（zcliang21@m.fudan.edu.cn）

密码学是现代网络安全的基石.现阶段广泛使用的公钥密码体制，如公钥加密、密钥封装、数字签名等，多数是基于经典的困难问题构造的，如求解大整数分解、（椭圆）离散对数等困难问题.这些密码方案在当今互联网协议，如SSL/TLS，ІPSec 等中扮演了无可替代的角色，如保证通信内容的机密性、通信双方的身份认证、消息的完整性等.尽管针对这些数论问题目前最好的经典求解算法的时间复杂度是指数或亚指数级别，至少是超多项式级别的，但近些年来随着量子计算的飞速发展，已有相关研究表明存在多项式时间的量子算法可以完全求解它们.例如，美国科学家Shor[1]提出可在量子计算机中以多项式时间求解大整数分解和（椭圆）离散对数问题的量子算法.量子计算相关技术的发展日新月异.考虑到量子计算技术对现有公钥密码的颠覆性威胁，目前很多国家、公司和学术界已提前研究和布局能够抵抗量子攻击的密码学—后量子密码学（post-quantum cryptography，PQC）.

事实上，早在2016 年，美国国家标准技术研究所（National Іnstitute of Standards and Technology，NІST）已经正式开启了对公钥加密（public key encryption，PKE）方案、密钥封装方案（key encapsulation mechanism，KEM）和数字签名这3 种密钥原语的后量子密码方案标准征集活动，且目前已经评选出第3轮结果并选定拟标准化的方案[2].我国也在2019 年举行后量子密码算法竞赛，并于2020 年评选出获奖方案[3].

目前，后量子密码学的类型主要分为：基于哈希的、基于多变量的、基于同源的、基于编码的以及基于格的.其中基于格构造的后量子密码方案不仅具有平均情形到最糟情形的困难性规约，还在安全性、通信带宽和计算效率等方面表现均衡.在美国NІST和我国举办的后量子密码方案征集活动中，基于格的密码方案占据多数.例如，NІST 第1 轮64 个方案中的26 个[4]、第2 轮26 个方案中的12 个[5]、第3 轮15 个方案中的7 个[6]以及拟标准化4 个方案中的3个[2]均为基于格构造的密码方案.我国后量子密码算法设计竞赛获奖方案共14 个，其中有11 个均为基于格构造的.基于格的方案在设计PKE 和KEM 时主要基于一般格、理想格、模格和NTRU 格.常用的格困难问题主要分为2 类：第1 类是{R,M}LWE/LWR 问题[7-10]；第2 类是NTRU 格相关问题[11-13].

NTRU 最早由Hoffstein 等人[14]于1996 年美密会讨论环节中提出，但它在1997 年遭遇格攻击[15].随后Hoffstein 等人对方案安全性方面进行补救，并于1998 年正式提出NTRU 加密方案（NTRU-HPS）[11].该方案是第1 个基于格困难问题构造的现实的公钥加密方案.NTRU 相关问题目前已经是许多密码方案中的基础元件[16-18].在NІST 的后量子密码方案征集项目中，基于NTRU 格的方案具有举足轻重的地位.具体而言，Falcon 数字签名[19]基于NTRU 格构造，且是NІST 后量子密码方案标准征集拟标准化的数字签名之一.另外，在NІST 第3 轮中，NTRU KEM[20]（包含NTRU-HRSS 和NTRUEncrypt）是4 个决赛KEM 方案之 一，NTRU Prime KEM[21]（包 含SNTRU Prime 和NTRU LPRime）是5 个候选方案之一.尽管目前NІST 选择了基于模格的Kyber[22]作为唯一的拟标准化KEM方案[2]，而基于NTRU 格的方案没能被NІST 选为拟标准化KEM 方案，但NІST 官方报告声称如果Kyber相关专利问题未能得到很好地解决，仍可能会放弃Kyber 而启用NTRU KEM[23].另外，在2011 年NTRUEncrypt 方案便已入选X9.98 标准并应用于金融服务企业之中[24].自2022 年4 月起，国际标准OpenSSH更新了版本9.0 之后，OpenSSH 便采用了NTRU Prime KEM 方案结合X25519 ECDH 方案的混合模式，以抵抗“先捕获后解密”攻击[25].另外，有关基于NTRU 格的方案的研究并不应因此而止步不前，对基于NTRU格的方案的设计和分析理应得到更充分、深入和全面的研究.

基于NTRU 格设计的KEM 备受青睐，主要原因有3 点：1）基于NTRU 格的KEM 具有坚固的安全保障.自NTRU 被提出至今，有关NTRU 的攻击和密码分析对基于NTRU 格的KEM 安全性产生的影响非常有限.事实上，大多数基于NTRU 相关困难问题设计的密码方案至今没被攻破.2）有关NTRU 的专利已失效.在1997 年，NTRU 加密系统获得了专利，但在2017 年NTRU 相关核心专利已到期.3）大多数基于NTRU 格的KEM 结构简单，便于实现，同时加解密算法的运算速度快[20-21].

近些年来，针对基于NTRU 格的KEM 有2 点可优化的方向：

1）计算效率方面.基于NTRU 格的KEM 如NTRUHRSS[20]和SNTRU Prime[21]在计算效率方面逊色于基于{R,M}LWE 的方案.主要是因为后者能够使用高效的数论变换（number theoretic transform，NTT）来计算多项式乘法.近些年来，文献[26-27]基于NTT 友好的多项式环来构造出基于NTRU 格的KEM，使得方案中的多项式运算得到高效计算.

2）密文尺寸方面.降低密文尺寸对网络协议，如TLS 和ІoT 资源受限设备通信都具有积极的作用.尽管密文压缩在基于LWE 及其变体的KEM 中是一项成熟的技术，但对基于NTRU 格的KEM 来说，目前相关研究极少.常见的NTRU 的加密方案的密文形式一般为c=phr+mmodq，其中h为公钥（一般h=g/f），q为方案模数，g、f为秘密多项式；r为采样得到的秘密多项式，m为待加密的明文，p为明文空间模数.这可视为m通过编码到密文c的低位.解密算法将c乘以私钥f，得到cfmodq=pgr+mf.随后通过乘f的逆，或当f=pf′+1 时可通过模p消除杂项来恢复明文.这种解密机制要求被消除的杂项为p的倍数.所以一旦密文c被压缩，压缩带来的误差往往集中在c的低位，从而破坏m的有效信息，此时便无法正确解密得到原始的m.

文献[28-29]对基于NTRU 格的KEM 的密文压缩进行了探索，但是文献[28-29]的方案有2 点不足.第1 点不足是这些方案都基于2 种困难性假设来构建KEM.其中文献[28]是基于NTRU 假设[11]和RLWE 假设[9]，文献[29]是基于NTRU 假设和RLWR假设[8].引入过多的困难性假设会导致方案建立在更理想化的假设上.同时，分析这些方案的安全强度则需要分析2 种困难性问题的安全强度，并取2 个安全强度的最小值.所以，方案的安全性很大程度上取决于安全强度更低的困难性问题.NTRU 相关困难问题的安全性经过20 多年的密码分析现今仍然安全；RLWE 和RLWR 是较之更新的问题而需要进一步密码分析和验证.为得到更为稳定的安全保障，仅基于NTRU 相关困难问题设计的KEM 值得深入地研究和探索.第2 点不足是文献[28-29]的方案均使用纠错码和复杂的纠错机制来恢复明文信息.其中文献[28]使用可尺度E8格纠错码；文献[29]使用改进的Babai算法.尽管纠错码具有良好的纠错能力从而有效恢复信息，但是KEM 使用纠错码会带来2 个缺点：1）纠错码增加了方案遭遇侧信道攻击的风险[30]，特别是计时攻击[31]；2）纠错码导致实现更复杂、更耗时，且更容易出错.为了设计更安全且便于实现的KEM，设计者应该避免使用纠错码.所以，对基于NTRU 格的KEM 来说，在不使用纠错码的情况下，如何得到可压缩密文的构造依然需要进一步探索.

在我国，后量子密码被我国科协列为60 个我国亟待解决的重大科技难题之一.尽管我国2019 年密码算法设计竞赛的获奖方案大多数是基于格构造的，且包含基于NTRU 格的FatSeal 签名[3]，但是在它们之中并没有基于NTRU 格的PKE 和KEM.在当前国内外网络空间安全愈发重要的大背景下，我国研究团队理应自主研制高性能、多样化的后量子密码方案.考虑到基于NTRU 格的方案在国际上（特别是NІST后量子密码标准征集项目）的重要地位，本文主要关注基于NTRU 格构造高效的PKE 和KEM，并针对目前可优化方向，如计算效率方面和密文尺寸方面，提出一套基于NTRU 格构造的可压缩密文的实用化公钥密码系统.本文旨在为后续同类后量子密码方案的研究和优化提供重要参考.同时，这方面的研究工作对我国未来的后量子密码标准的选拔、制定、推广和实际应用都具有重要的现实意义.

本文的贡献主要有4 点：

1）基于NTT 友好环 Zq[x]/(xn-xn/2+1)构造了一个基于NTRU 格的可压缩密文的密钥封装方案LTRU.该方案包含了ІND-CPA 安全的公钥加密方案LTRU.PKE 和ІND-CCA 安全的密钥封装方案LTRU.KEM.本文的LTRU 仅基于NTRU 单向困难性假设构建.LTRU 能够避免引入过多假设，从而避免方案假设过强和过于理想化.同时LTRU 不使用纠错码，从而实现更简单，且降低了遭遇侧信道攻击的风险.已知LTRU 是第1 个仅基于NTRU 类型假设且不使用纠错码也能压缩密文的密钥封装方案.

2）提供了针对128 b 安全强度的LTRU 参数集.这使得LTRU 不仅达到了目标安全强度（实际上达到129 b 量子安全强度），还具有与安全性匹配的、可忽略的错误率（2-154），同时通信带宽小于其他NTRU方案.具体而言，与NІST 第3 轮决赛方案NTRUHRSS 相比，LTRU 的经典安全强度和量子安全强度分别增强6 b 和5 b，并且LTRU 的公钥尺寸降低14.6%，密文尺寸降低26.0%，总带宽降低20.3%.

3）提出了一种高效的混合基NTT 算法.该算法能够有效计算环 Z2917[x]/(x648-x324+1)上的多项式运算，利用3 次单位根的性质来有效减少基-3 FFT trick步骤中一半的乘法数量，并利用1-迭代Karatsuba 算法来有效减少点乘中的乘法数量.通过具体实现的效率分析可知，跟未使用1-迭代Karatsuba 算法和单位根的性质优化乘法数量的NTT 算法相比，本文NTT 在正向变换、点乘和逆向变换的CPU 周期数分别降低24.9%，20.6%，26.8%，总共降低25.3%.

4）提供LTRU 的C 实现和AVX2 实现.实验结果表明，与NTRU-HRSS 的AVX2 实现相比，LTRU在密钥生成和解封装算法上分别快了10.9 倍和1.7倍，封装算法的速度则与NTRU-HRSS 的速度相当.

1 相关工作

近些年来，陆续有基于NTRU 格的方案被提出.Stehlé等人[32]基于2 次幂分圆环 Z[x]/(xn+1)（其中n为2 次幂）来设计基于NTRU 变体的PKE，并证明了公钥的安全性.随后，Wang 等人[33]将该方案推广至任意的分圆环.但是这2 个方案因为公钥尺寸过大而无法应用于实际的场景中.Jarvis 等人[34]将NTRUHPS 推广至Eisenstein 整数环 Z[ω]/(xn-1)（其中ω=exp(2π i/3)）.该方案在密钥尺寸和性能方面比NTRU-HPS 更有优势.Hülsing 等人[35]全面提升NTRUHPS 的密钥尺寸、密文尺寸和效率，并提出了NTRUHRSS.NTRU-HRSS 曾是NІST 后量子方案征集项目第3 轮决赛方案之一[20].Bernstein 等人[36]考虑到NTRU 类型方案使用的多项式环或因丰富的代数结构而遭受相关攻击，提出了使用代数结构更少的环Zq[x]/(xn-x-1)的NTRU 变体方案：NTRU Prime（其中n,q均为素数）.NTRU-prime 曾是NІST 后量子方案征集项目第3 轮候选方案之一[20].

为了追求更高的实现效率，Lyubashevsky 等人[26]在多项式环 Z7681[x]/(x768-x384+1)上构造了针对128 b安全强度的NTTRU 方案.随后，Duman 等人[27]将该方案推广至更一般的n并选择对应的q.但是这些方案均是遵循传统NTRU 的框架，并不能对密文进行压缩.

Fouque 等人[29]提出BAT 方案.BAT 与传统NTRU类型的KEM 的构造有所区别，但与Falcon 数字签名方案[19]有众多相似之处.BAT 的私钥是一组陷门基，这一点与Falcon 相似，但区别于其他NTRU 类型KEM 的私钥f.直观地理解，BAT 使用的纠错码机制相当于对含有2 个未知数的方程求解出秘密多项式和噪音多项式，并用来恢复明文.BAT 通过将密文构造为RLWR 实例的方式来降低密文的尺寸.然而，为生成陷门基作为私钥，BAT 的密钥生成算法速度比常见的NTRU 类型KEM 的速度慢约1 000 倍.其次，为降低密文尺寸而构造的RLWR 实例使用二元的秘密分布（即秘密多项式的系数选自{0,1}），而关于该问题的安全性目前还是公开问题且还需要进一步研究.另外，BAT 缺少匹配128 b 安全强度的参数集，因为它使用2 次幂分圆环 Z[x]/(xn+1)，且n=512和n=1 024，而前者的安全强度略低于128 b，后者的安全强度则远高于128 b.

2 预备知识

本节主要介绍一些符号说明、基本定义和密码原语等.

2.1 符号说明和基本定义

1）本文记 Z 为整数环，n和q为 某些整数.定 义集合Zq=Z/qZ ≅{0,1,…,q-1}.对 于实数x∈R，符 号表示对x四舍五入后的值.本文主要使用分圆多项式环 R:=Z[x]/(xn-xn/2+1) 及其商环Rq:=R/qR=Zq[x]/(xn-xn/2+1)，其中n=2i3j，i≥0，j＞1，且此时xn-xn/2+1是 3n阶分圆多项式.环 R（或 Rq）中的元素均是多项式，本文使用符号f的幂级数形式（或fi∈Zq）.一个函数 ε:N →[0,1]是可忽略的，指的是对任意的正数c以及充分大的 λ，ε(λ)＜1/λc成立.

2）模约减.对于某正整数q，符号r′=rmodq表示r落在 [0,q)∩Z 中的代表元r′.符号r′=rmod±q表示r落在中的代表元r′.另外，符号r′≡rmodq′表示r′和r模q同余.

3）元素的范数[37].对于元素v∈Zq，定义它的ℓ∞范数 ‖v‖∞为 ||vmod±q||.对于环 R（或 Rq）中的元素w，它的 ℓ∞范数为

4）压缩函数和解压缩函数[37].对于正整数q和d，定义压缩函数

以及解压缩函数

且对于任意的x∈Zq，有

5）集合和分布.对于集合D，记x←$D表示从D中均匀随机选 取x.如果D是一个概率分布，x←D表示根据分布D采样得到x.本文主要使用的分布为：采样 (a1,a2,…,aη,b1,b2,…,bη)←${0,1}2η，然后输出根据分布D，采样多项式f指的是f的每一个系数均根据D采样得到.

2.2 密码原语

1）公钥加密方案

一个公钥加密方案PKE 包含KeyGen,Enc,Dec3个概率多项式时间（probabilistic polynomial time，PPT）算法，记其明文空间为 M.密钥生成算法KeyGen输出公私钥对 (pk,sk).加密算法Enc输入公钥pk和明文m∈M，输出密文ct.本文在必要时使用Enc(pk,m;coin) 显式表示加密算法使用的随机数为coin.确定性的解密算法Dec输入密文ct和私钥sk，输出m∈M，或者 ⊥表示解密失败.公钥加密方案的解密错误率δ定义为

其中期望作用于 (pk,sk)←KeyGen上，式（1）概率取自加密算法Enc使用的随机数.一个公钥加密方案是抗原像恢复意义下的选择明文PRE-CPA（preimage resistance under chosen-plaintext attacks）安全的[27]，指的是对于任意PPT 敌手 A，其优势是可忽略的：

一个公钥加密方案是不可区分意义下的选择明文ІND-CPA（indistinguishability under chosen-plaintext attacks）安全的，指的是对于任意PPT 敌手 A，其优势是可忽略的：

2）密钥封装方案

一个密钥封装方案KEM 包含KeyGen,Encaps,Decaps3 个PPT 算法.记其导出密钥空间为 K.密钥生成算法KeyGen输出公私钥对 (pk,sk).密钥封装算法Encaps输入公钥pk，输出密文ct和密钥K∈K.确定性的解封装算法Decaps输入密文ct和私钥sk，输出K∈K，或者 ⊥表示解封装失败.密钥封装方案的错误率 δ定义为Pr[Decaps(sk,ct)≠K:(ct,K)←Encaps(pk)]＜δ，其中概率取自 (pk,sk)←KeyGen和封装算法Encaps使用的随机数.一个密钥封装方案是不可区分意义下的选择密文ІND-CCA（indistinguishability under chosenciphertext attacks）安全的，指的是对于任意PPT 敌手A，其优势是可忽略的：

2.3 NTRU 单向困难性假设

定义1.NTRU 单向困难性假设[12-13].给定NTRU公钥加密方案的公钥h以及PPT 加密算法Enc，则NTRU 单向函数是指

其中Enc(h,(r,e)) 指的是以h，e，r作为加密算法的输入，在NTRU 公钥加密方案中 Le一般是它的明文空间，Lr一般是它的随机数空间.

NTRU 单向问题NTRU-OW（NTRU one-wayness）指的是给定公钥h和密文多项式c，计算得到 (r,e).NTRU 单向问题是困难的，指的是对于任意PPT 敌手A，其优势是可忽略的：

通俗来讲，NTRU 单向困难性假设是指没有PPT敌手能够从公钥h和密文c中恢复出 (r,e).原始的NTRU-HPS 方案[11]便蕴含了NTRU 单向困难性假设，直到文献[12-13]将NTRU 单向困难性假设提炼出来，并应用在基于NTRU 格的方案（如NAEP 方案）的安全性证明之中.

2.4 ACWC0 转换

定义2.ACWC0转换[27].记PKE1=（KeyGen1,Enc1,Dec1）为公钥加密方案，其明文空间记为 M1.令F :{0,1}*→{0,1}λ为哈希函数，λ为某正整数.ACWC0通过算法1～3 将PKE1=（KeyGen1,Enc1,Dec1）转换得到另一个公钥加密方案PKE2=（KeyGen2,Enc2,Dec2），其明文空间为 M2={0,1}λ.

算法1.密钥生成算法KeyGen2.

根据文献[27]中的引理2.2 和定理3.3，PKE2方案在随机预言机模型（random oracle model，ROM）[38]下的ІND-CPA 安全性由定理1 给出.

定理1.在随机预言机模型下，对于任意的攻击PKE2的ІND-CPA 安全性的敌手 A，存在攻击PKE1的PRECPA 安全性的敌手 B，其运行时间与 A相当，使得

另外，根据文献[27]中的引理2.2 和定理3.4，可得定理2 关于PKE2方案在量子随机预言机模型（quantum random oracle model，QROM）[39]下 的ІNDCPA 安全性.

定理2.在量子随机预言机模型下，对于任意的攻击PKE2的ІND-CPA 安全性的量子敌手 A，存在攻击PKE1的PRE-CPA 安全性的量子敌手 B，其运行时间与 A相当，使得

其中dF是 A 查询 F的深度.

可见，ACWC0转换能够将一个PRE-CPA 安全的公钥加密方案转换得到另一个ІND-CPA 安全的公钥加密方案.本文将在3.1 节中提出的公钥加密方案便是通过ACWC0转换得到的.

2.5 数论变换（NTT）

NTT 是快速傅里叶变换（fast Fourier transform，FFT）在有限域上的特殊形式.NTT 是计算高次多项式乘法最高效的算法，其复杂度为O(nlogn)，其中n为被乘多项式的维度.简单地说，基于NTT 计算多项式乘 法h=fg的过程为h=INT T(NT T(f)◦NT T(g))，其中 NT T 表示正向变换，INT T 表示逆向变换，“ ◦”表示点乘.本文沿用文献[40]有关多项式乘法的符号和术语，FFT trick 是计算NTT 的一种快速算法，其计算过程本质是基于多项式环形式的中国剩余定理（Chinese remainder theorem，CRT），即给定两两互素的多项式g1,g2,…,gk，有CRT 同构

并且 φ(f)=(fmodg1,fmodg2,…,fmodgk).记 ζ 在Zq中可逆.对于经典的基-2 FFT trick 的情况，有CRT 同构：

其中 ρ是3 次单位根.混合基NTT 指的是在计算NTT过程含有多种FFT trick.

2.6 Karatsuba 算法

定义3.1-迭代Karatsuba 算法[43].设a,b,c,d为 某些数或多项式.1-迭代Karatsuba 算法指的是为了计算t1=ac，t2=ad+bc和t3=bd，可以先计算t1和t3，然 后通过t2=(a+b)(c+d)-t1-t3计算t2.该算法能在增加3 个加（减）法的代价上，减少1 个乘法.

3 本文方案及其分析

下面介绍本文提出的基于NTRU 格构造的可压缩密文的密钥封装方案LTRU.LTRU 包括一个ІNDCPA 安全的公钥加密方案LTRU.PKE，以及一个ІNDCCA 安全的密钥封装方案LTRU.KEM，其中该KEM通过FO（Fujisaki-Okamoto）转换[44-45]得到.LTRU.PKE是由底层公钥加密方案PKE′=（KeyGen,Enc′,Dec′）结合文献[27]的ACWC0转换得到的.底层公钥加密方案PKE′将在3.4 节中展示，但它只能满足PRECPA 安全性，并且目前还没有相关文献论证FO 转换将PRE-CPA 安全的公钥加密方案转换得到ІNDCCA 安全的KEM 的规约上界.本文通过增加ACWC0转换，将底层公钥加密方案PKE′转换得到ІND-CPA安全的LTRU.PKE，然后便能通过FO 转换得到ІNDCCA 安全的KEM.

3.1 LTRU 的构造

LTRU.PKE 的具体构造见算法4～6.记其明文空间为 M={0,1}λ，其中 λ 为正整数.记多项式环为Rq=Zq[x]/(xn-xn/2+1)，其中n和q是环参数.记d和p为 正整数，且p和q互素.需要说明的是，在算法4～6 中，为了给出一般的构造框架，本文使用的分布 ψ 泛指 R上的某分布，但事实上，在3.3 节的具体参数选择方面，本文实例化 ψ 为参数 η=2 的分布（定 义见2.1 节）.令F :{0,1}*→{0,1}λ为哈希函数.本文主要考虑p=2以及 λ=256 的情况.可 视 {0,1}n中的元素是维度为n、系数为0 或1 的多项式.压缩函数Compress和解压缩函数Decompress的具体计算过程见2.1 节.

算法4.密钥生成算法LTRU.PKE.KeyGen.

可见，LTRU.PKE 应用了ACWC0转换[27]，见算法5 行③以及算法6 行③.LTRU.KEM 是由LTRU.PKE通过转换得到，其中是文献[45]提出的FO转换的一个变体.LTRU.KEM 的密钥生成算法KeyGen与LTRU.PKE 的KeyGen相 同.LTRU.KEM 的封装算法和解封装算法分别见算法7 和算法8.记K为LTRU.KEM 的导出密钥空间，为方便起见，本文令K={0,1}256.记 COINS为LTRU 公钥加密方案中加密算法所使用的随机数空间.记H :{0,1}*→K×COINS为哈希函数.实际上，H能够拆分为2 部分 H1和 H2，记 H1为 H 映射到 COINS 的部分，H2为 H 映射到K的部分.在算法7 的行②中可以先使用 H1生成coin，在行③中计算得到密文c之后，再使用 H2生成共享密钥K.

算法7.封装算法LTRU.KEM.Encaps.

算法8.解封装算法LTRU.KEM.Decaps.

3.2 错误率分析

则LTRU 的错误率为 δ.

证明.

从2.1 节的压缩函数Compress和解压缩函数Decompress的定义可知，算法6 行①的c′可以表示为

由于LTRU 中h=g/f和f=2f′+1，则可得

本文计算错误率的方法论和Python 脚本源自文献[22,26,37].值得注意的是，文献[26]将环Z[x]/(xnxn/2+1) 上的多项式的乘积的系数视为由n/2个形如ab+b′(a+a′) 的元组构成，其中a,a′,b,b′的分布由被乘多项式的分布决定.尽管该环上的多项式的乘积另外还包含形如ab+a′b′的元组，文献[26]建议全部使用ab+b′(a+a′)的形式，因为该形式具有更宽泛的分布，且能得到更保守估计的错误率结果.

3.3 参数选择

本节给出LTRU 的推荐参数集，其主要针对128 b安全强度，如表1 所示.Rq是多项式环，维数n和模数q是环参数.本文选择NTT 友好的q，旨在q允许在Rq上执行高效的多项式乘法和除法，具体细节见第4 节.p是明文空间模数；d是压缩参数；ψ是概率分布，本文主要考虑分布即参数为 η=2 的分布，的定义见2.1 节；|pk|，|ct|，B.W.分别是公钥尺寸、密文尺寸和带宽（公钥尺寸+密文尺寸），单位均为B；Sec-（C,Q）是该参数集的NTRU 安全强度（单位为b），C 表示经典安全强度，Q 表示量子安全强度，安全强度的分析见3.5 节；δ是该参数集的错误率，其细节见3.2 节.

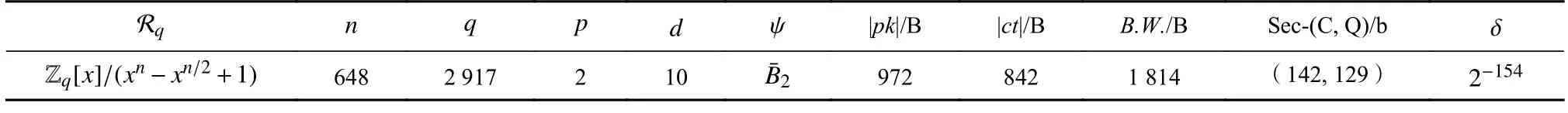
Table 1 Recommended Parameter Set of LTRU表1 LTRU 的推荐参数集

3.4 安全规约

下面将基于NTRU 单向困难性假设，证明LTRU.PKE 是ІND-CPA 安全的.

定理4.ІND-CPA 安全性.对于任意的概率多项式时间敌手 A，存在概率多项式时间敌手 B，其运行时间与 A相当，使得：

证明.LTRU.PKE 方案由底层公钥加密方案PKE′=（KeyGen,Enc′,Dec′）结合文献[27]的ACWC0转换得到，其中底层公钥加密方案PKE′的KeyGen算法与LTRU.PKE 方案的一致，Enc′算法和Dec′算法分别见算法9 和算法10.

算法9.加密算法PKE′.Enc′.

算法10.解密算法PKE′.Dec′.

由定理1 和定理2 可知，当底层公钥加密方案PKE′满足PRE-CPA 安全性时，经过ACWC0转换得到的LTRU.PKE 方案满足ІND-CPA 安全性.下面将通过Game-Hopping 技术[46]来证明底层公钥加密方案PKE′的PRE-CPA 安全性.

记 A 是攻击PKE′方案的PRE-CPA 安全性的概率多项式时间敌手.考虑游戏G0和G1.记事件S ucci为敌手 A 在游戏Gi中获胜，即游戏Gi的输出满足c=c*.

游戏G0是 关于PKE′方案原始的PRE-CPA 游戏.根据PRE-CPA 安全性的定义，可知

游戏G1是在游戏G0的基础上，取消对行⑦挑战密文c*的压缩操作.所以，敌手 A 在游戏G1中拥有的挑战密文的信息至少比在游戏G0中的多.可见，游戏G0的困难性至少与游戏G1的相同，则

整合游戏G0和G1中的概率可知，对于概率多项式时间敌手 A，存在概率多项式时间敌手 B，使得

再根据定理1 和定理2，由PKE′方案的PRE-CPA 安全性可得到LTRU.PKE 的ІND-CPA 安全性，其对应的规约上界正如定理4 所示.综上，命题得证.证毕.

从定理4 可知，若NTRU 单向困难性问题是困难的，那么LTRU.PKE 是ІND-CPA 安全的.由于LTRU.KEM 是从ІND-CPA 安全的LTRU.PKE 通 过变换得到，根据文献[45,47]，LTRU.KEM 在经典随机预言机和量子随机预言机下的ІND-CCA 安全性由定理5给出.

定理5.ІND-CCA 安全性[45,47].在记 γ 和 δ分别是LTRU.PKE 的弱spread 参数[45,47]和解密错误率.对于任意攻击LTRU.KEM 的 ІND-CCA 安全性的概率多项式时间敌手 A，存在攻击LTRU.PKE 的ІND-CPA安全性的概率多项式时间敌手 B，使得：

1）在经典随机预言机模型下，将 H建模为经典随机预言机，A查询至多qH次 H，查询至多qD次解封装预言机，B的运行时间和 A的相当，则有

2）在量子随机预言机模型下，A 和 B为量子敌手，且将 H建模为量子随机预言机，A以量子方式查询至多qH次 H，以经典方式查询至多qD次解封装预言机，则有

其中qT:=2(qH+qD)，并且

3.5 安全强度

对于基于NTRU 格构造的KEM 来说，格攻击是目前最有效的攻击.本节主要从常用的格攻击来分析LTRU 的安全强度.

1）NTRU 格

起初，基于NTRU 格构造的方案均是依赖于多项式环上的困难性问题.然而，Coppersmith 等人[15]提出针对基于NTRU 格构造方案的格攻击，它的核心思想是构造NTRU 格.本文方案的公钥对应的NTRU格L(B)⊂Z2n的基矩阵为

其中In是n维单位矩阵，Rot(h)是h的循环移位矩阵，即它的第i行向量对应xihmodxn-xn/2+1.文献[15]提出，秘密 (f,g) 及其循环移位向量是格 L(B)的最短向量.事实上，NTRU 类型方案的格攻击流程为：通过格基约化算法求解格 L(B)的唯一最短向量问题（unique-short vector problem，u-SVP），找到该最短向量之后转化得到方案的私钥[15].

2）原始攻击

原始攻击通过构造一个整数嵌入格，如Kannan嵌入[48]和Bai-Galbraith 嵌入[49]等来求解u-SVP 问题.目前主要的格基约化算法为BKZ 算法[50-51].给定格L(B)的一组基，BKZ 算法运行时将格划分为多个低维度格，并把这些低维度格的维度记为b.然后在b维格中求解最短向量问题（short vector problem，SVP），所使用的方法有筛法和枚举.根据文献[52]的core-SVP 方法论，对于b维格上求解SVP 问题，目前最优的经典算法的复杂度为 20.292b，最优的量子算法的复杂度为 20.265b.core-SVP 方法论将这些复杂度视为求解b维格SVP 问题的复杂度，并将得到的BKZ 算法的复杂度作为原始攻击的复杂度估计.本文将基于core-SVP 方法论给本文方案提供一个保守估计的安全强度，并基于文献[22,37,52]提供的计算安全强度的Python 脚本来计算LTRU 在原始攻击下的经典安全强度和量子安全强度，其详细结果如表1 所示.

3）其他攻击

对偶攻击主要通过将判定型LWE 问题规约为短整数解问题（short integer solution problem，SІS）的方式来求解判定型LWE 问题.由于对偶攻击不适用于NTRU 类型的方案[53]，故本文不考虑对偶攻击对LTRU的影响.过度拉伸NTRU 攻击[54]的适用范围为模数q远大于秘密多项式系数的情况.由于LTRU 的模数q数值较小，不满足该情况，故本文不考虑该攻击.混合攻击[55]是格攻击和中间相遇攻击的提升版本，但混合攻击对于有着稀疏分布的秘密多项式系数和噪音多项式系数的方案能取得显著效果.然而对于LTRU，混合攻击不如原始攻击有效，因为LTRU 的秘密 (f,g)并非稀疏分布，不符合混合攻击的条件.

3.6 分析和讨论

1）多项式环

本文LTRU 方案使用第 3n个分圆多项式环Zq[x]/(xn-xn/2+1)，其中n的形式为 3l×2e，q为某些素数.主要原因是，当选择合适的q，如NTT 友好的q时，存在高效的NTT 算法计算该环上的多项式乘法和除法.同时，n的选择具有更大的灵活性，因为n能够选择576，768，864，972，1 152，1 296 等数值.当选择其他的n值时，LTRU 能够达到其他的安全强度（如192 b和256 b），而不再局限于128 b 的安全强度.但是，本文主要针对128 b 的安全强度，故选择n=648.相比而言，NTRU-HRSS[20]使用多项式环 Zq[x]/(xn-1)，其中n为素数，q为2 次幂；SNTRU Prime[21]使用多项式环Zq[x]/(xn-x-1)，其中n，q均为素数.这些多项式环不是NTT 友好环，所以这些多项式环上的多项式乘法和除法更复杂，且耗时更多.

2）明文空间模数p

与其他NTRU 方案如文献[20-21,26-27]中的方案不同，本文LTRU 使用的明文空间模数p=2，且只需出现在私钥f中，即f=pf′+1，而无需在公钥h以及解密算法中出现.但是，NTRU 方案[20-21,26-27]使用模数p=3.甚至，由于NTRU 类型方案要求q和p互素，而NTRU-HRSS[20]由于使用2 次幂的模数q，所以它使用了与q互素的最小整数p=3.

3）纠错机制

常见的NTRU 类型方案[20-21,26-27]的密文形式为c=phr+mmodq，这可以视为明文m编码在密文c的低位.其恢复明文m的方式主要通过计算cfmodq之后再模p来消去杂项.这种纠错机制依赖于杂项是p的倍数.与之不同的是，LTRU 在底层公钥加密方案PKE′中首先将明文m提升q/2 倍，相当于把明文m编码到密文c的高位，随后在解密算法中只要求杂项的范数小于 1/2，而不必要求其为p的倍数.同时可以看到，LTRU 不使用纠错码来恢复明文.纠错码虽然能够高效地实现纠错来恢复明文，但是纠错码使得代码实现更复杂且增加遭遇侧信道攻击的风险，如文献[30]针对纠错码提出了有效的侧信道攻击.

4）密文压缩

LTRU 的密文压缩操作见算法5 的行②.本文的LTRU 是第1 个仅基于NTRU 单向困难性假设构造的、不使用纠错码也能够压缩密文的密钥封装方案.LTRU 的密钥压缩参数d可根据需求自行调整.对于其他NTRU 类型方案[20-21,26-27]，如果它们压缩密文，那么压缩过程会在密文的低位带来误差，而编码在密文低位的明文m的有效信息会被这些误差破坏，使得正确的明文m难以恢复出来；同时在解密算法中杂项也不再是p的倍数，所以也无法通过模p来消去杂项以恢复正确的明文m.

4 高效的混合基数论变换

本节将介绍本文提出的一种混合基NTT 算法，其能高效地计算本文推荐参数集LTRU-648 所使用的 环 Zq[x]/(xn-xn/2+1)，n=648，q=2 917上的多项式乘法和除法，且利用了1-迭代Karatsuba 算法和单位根的性质减少乘法的数量，以提高计算效率.

对于 Zq[x]/(xn-xn/2+1)，n=648，q=2 917，可 知Zq中存在 3n/2 次本原单位根 ζ=2，其中ζ为k次本原单位根是指ζk≡1modq且ζi≠1modq，0＜i＜k.

4.1 正向变换

为方便理解，图1 展示了混合基NTT 对应的CRT 同构树形图.本文的混合基NTT 的计算过程主要依靠逐层CRT 分解.

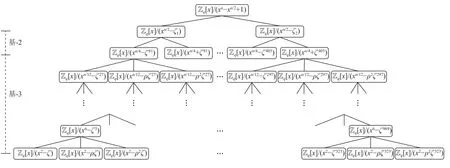
Fig.1 The tree map of CRT isomorphism图1 CRT 同构的树形图

类似于文献[26]提出的第1 层CRT 同构，对于Zq[x]/(xn-xn/2+1)，有

其中 ζ1+ζ2=1 和 ζ1ζ2=1.容易求得，ζ2=1-ζ1和取ζ1=ζn/4modq以 及 ζ2=ζ5n/4modq，对于任意的f∈Zq[x]/(xn-xn/2+1)，可得

由于 ζ1fn/2只需计算1 次而可使用2 次，故式（2）（3）总计只需n/2 个乘法和n个加（减）法.

1）基-2 FFT trick 步骤

可利用CRT 对 Zq[x]/(xn/2-ζ1) 和 Zq[x]/(xn/2-ζ2)进行基-2 FFT trick 步骤的分解.对于每个基-2 FFT trick步骤形如

其中r为 ζ 的某次幂，对于f′∈Zq[x]/(x2m-r2)，可得

其中每个r fi′只需计算1 次而可使用2 次.这使得每层的基-2 FFT trick 步骤所需乘法数量从n个锐减到n/2个.

2）基-3 FFT trick 步骤

对于n=648，基-2 FFT trick 步骤可进行1 层，直至得到4 个形如 Zq[x]/(x162-ζ81)的项.此时本文采用基-3 FFT trick.每个基-3 FFT trick 步骤均形如

其中r为 ζ 的某次幂，ρ=ζn/3modq为3 次单位根.Zq[x]/(x3m-r3) 中的多项式f′′可以表示为

其中fa,fb,fc均为m-1 次多项式.由于 ρ3=1 modq，可得

注意到ρ2+ρ+1=0 modq，则 ρ2=-ρ-1 modq.类似于文献[56]，此时有

以及

于是可得

注意到，r fb,r2fc,ρ(r fb-r2fc)都只需要计算1 次而能够多次使用.并且只需存储和使用本原单位根r和r2以及3 次单位根 ρ，而无需存储其他值如 ρr，ρ2r2，ρ2r，ρr2.易知，使用3 次单位根的性质之后，每层的基-3 FFT trick 步骤所需乘法数量从 2n个锐减到n个.

正向变换中基-3 FFT trick 步骤可进行4 层，直到将Zq[x]/(xn-xn/2+1) 分解得到n/2个模2 次多项式的环.换句话说，即有

其中 τ(i) 表示第i个环中 ζ的幂且序号从0 开始.对于f∈Zq[x]/(xn-xn/2+1)，其正向变换的结果记为

为方便后文书写，本文使用符号 NT T表示上述的正向变换过程.正向变换 NT T的伪代码见算法11.

算法11.正向变换 NT T.

4.2 逆向变换

逆向变换可由正向变换的逆过程得到.本文使用符号 INT T表示逆向变换.值得注意的是，在计算基-3 逆向FFT trick 时，同样可利用3 次单位根的性质减少乘法的数量.沿用4.1 节的符号和Zq[x]/(x3m-r3) 示例，在基-3 逆向FFT trick 中，从fx,fy,fz计算得到f′′.由f′′=fa+fbxm+fcx2m可知，这等价于得到fa,fb,fc.先计算

利用ρ2=-ρ-1 modq，进一步可得

以及

于是可得

其中倍数 3-1可延迟处理.故易知，基于3 次单位根的性质，每层的基-3 逆向FFT trick 步骤所需乘法数量从 2n个锐减到n个.

另外，对于基-2 逆向FFT trick，在此沿用4.1 节的示例，从fl=f′modxm-r和fr=f′modxm+r计算得到f′∈Zq[x]/(x2m-r2)的步骤为

其中fl,i和fr,i分别表示fl和fr的第i个系数，倍数 2-1同样可延迟处理.易知，每层的基-2 逆向FFT trick 步骤共需要n/2个乘法.再合计上基-3 逆向FFT trick 步骤延迟处理的倍数，在整个逆向变换结束之时，需要乘以总的倍数 (n/2)-1modq.

逆向变换 INT T 的伪代码见算法12.

算法12.逆向变换 INT T.

4.3 点 乘

原本需要5 个乘法，现在只需要4 个乘法.使用1-迭代Karatsuba 算法计算点乘的伪代码见算法13.

算法13.点乘.

4.4 基于混合基NTT 的多项式运算

基于混合基NTT 计算多项式乘法h=fg∈Zq[x]/(xn-xn/2+1)的过程为

另外，本文同样使用该混合基NTT 计算多项式除法h=g/f∈Zq[x]/(xn-xn/2+1)，即计算LTRU 方案中的公钥h.具体而言，其计算过程为

算法14.计算低次数多项式的逆.

5 实现细节

本文给出了LTRU 的便携C 实现和优化AVX2实现.下面将简要介绍LTRU 的一些实现细节.值得注意的是，LTRU 的所有实现均采用了常数时间实现技巧，以抵抗一些潜在的侧信道攻击，特别是计时攻击[31].

5.1 基本构件

本文使用的模数q=2 917是低于16 b 的素数，所以Zq[x]/(xn-xn/2+1) 中的多项式能够使用长度为n、类型为16 b 有符号整型的数组来存储.

1）哈希函数

本文中使用的哈希函数均使用SHA3 系列函数来实例化.具体而言，使用SHA3-256 实例化哈希函数 F，使用SHA3-512 实例化哈希函数 H.其中 H以明文消息m作为输入，得到64 B 的输出，其中前32 B 作为导出的共享密钥，后32 B 作为种子并使用SHAKE128 来生成加密算法所需的随机数.

2）秘密多项式

本文使用的秘密多项式如f′,g,r都是根据分布采样得到.每采样一个系数需要4 个随机比特，所以采样一个多项式需要 4n个比特，即n/2字节.

3）约减算法

在计算多项式系数的加法和乘法时，计算结果存在超出16 b 有符号整型的有效表示范围的可能性.此时需要使用约减算法将计算结果约减到 [0,q).本文使用Barrett 约减算法[57]和Montgomery 约减算法[58].其中Barrett 约减算法主要用于系数加法后的约减；而Montgomery 约减算法主要用于系数和系数相乘，或者系数和本原单位根相乘时的约减.

4）消息的存储形式

注意到在LTRU 加密算法中，多项式e是系数范围取自 {0,1} 的多项式，所以可以将e视为大小为n的比特串.实际上，本文使用n/8 个字节（即n位）来存储并表示e，这样能够减少将e在多项式和比特串之间转换的过程，提高效率.

5）公私钥和密文

5.2 C 实现

本节提供LTRU 的C 实现的细节.本文使用第4节的高效的混合基NTT 来计算LTRU-648 的多项式乘法和除法（即计算公钥h）.测试设备为：硬件配置为2.3 GHz 的Іntel®Core™ i7-10510U CPU 和16 GB 内存的笔记本电脑，且关闭Turbo Boost 和Hyperthreading.操作系统为：核为Linux Kernel 4.4.0 的Ubuntu 20.04 LTS 操作系统，且gcc 版本为9.4.0.编译参数为：-Wallmarch=native-mtune=native-O3-fomit-framepointer-Wnounknown-pragmas.

本文LTRU 的C 实现只涉及到整型算术操作，特别是16 b 有符号整型算术.在NTT 的实现中，由于C 语言的“%”运算符不是常数时间实现，其执行时间和输入数据长度密切相关，存在泄露秘密数据的可能性，故本文转向使用常数时间实现的Barrett约减算法和Montgomery 约减算法.对于正向NTT 变换，本文使用延迟规约策略[59]来减少约减的次数.具体而言，对于乘法中使用的Montgomery 约减，其输出值范围为 [-q,q].本文使用的模数q为12 b，所以在6层FFT trick 之后，正向NTT 变换输出的多项式范围在 [-7q,7q]之间，这显然在16 b 有符号整型的有效表示范围之内.故中间计算过程无需进行额外的Barrett 约减，而只需要在正向NTT 变换结束时进行1 次Barrett 约减.

5.3 AVX2 实现

本节提供LTRU 的AVX2 实现细节.AVX2 实现主要优化的运算包括：多项式加法/乘法/除法、模约减算法等.但是，SHA3 系列哈希函数并没采用AVX2 优化实现，而是继续采用C 语言的实现.这是因为SHA3 系列哈希函数难以向量化实现，而目前最高效的实现是基于C 语言的[52].另外，NTT 运算非常耗时，所以NTT 运算是AVX2 优化的主要目标.下面主要介绍本文提出的混合基NTT 的AVX2 实现细节.

AVX2 指令集的载入/存储指令一次性载入/存储的数据长度为256 b.换句话说，指令能够一次性载入/存储16 个多项式系数，因为每个系数使用16 b 有符号整型表示.但是，每个多项式共有 648个系数，其中648 并非16 的整数倍.为了能够使用AVX2 指令集的载入/存储指令，将648 个系数对相邻的16 个系数进行划分，得到40 个划分单位以及剩下的8 个系数，然后对每个划分单位进行数据对齐.这种方法虽然便于使用载入/存储指令，但不便于在NTT 运算中计算基-2 FFT trick 步骤和基-3 FFT trick 步骤.

为了方便使用AVX2 指令集的载入/存储指令，同时方便计算基-2 FFT trick 步骤和基-3 FFT trick 步骤，本文采用2 个系数填充过程：

1）将648 个系数对相邻的12 个系数进行划分，得到54 个划分单位；

2）把每一个划分单位里面的12 个系数拓展到16 个系数，即保留原12 个系数位置不变，在它们末尾的位置填充4 个0.

通过这2 个系数填充过程，得到864 个系数，以及新的54 个划分单位，每个划分单位包含16 个系数.此时每个划分单位能够一次性被载入到寄存器之中.在完成寄存器一系列计算、存储回内存位置后，多项式系数提取的过程为：

1）将864 个系数对相邻的16 个系数进行划分，得到54 个划分单位；

2）在每一个划分单位中提取前面的12 个系数，舍弃末尾的4 个0.

通过这2 个系数提取过程，得到原始长度的多项式数组.系数填充过程和系数提取过程如图2 所示.

Fig.2 The padding and extraction of coefficients图2 系数的填充与提取

这种填充过程应用在多项式的NTT 运算，如正向变换、逆向变换、点乘和求逆之中.另外，这种填充过程使得NTT 运算以12 倍的并行度进行计算，区别于通常的16 倍的并行度计算.这是因为此时每个寄存器只能一次性处理原始多项式的12 个系数，而非原始多项式的16 个系数.由于AVX2 指令集的载入/存储指令耗时较多，所以应该减少内存访问的次数.常用的方法是合并处理NTT 运算中的若干层.本文合并正向变换的第2 层和第3 层的计算.在此期间，仅需载入一次数据，无需额外的访问内存和数据载入/存储便能够完成第2 层和第3 层的计算，这能够降低因载入/存储指令带来的CPU 周期数的消耗.本文通过vmovdqa指令完成数据的载入/存储.在分别载入多项式系数和本原单位根之后，通过vpmulhw指令和vpmullw指令分别计算它们乘积的高位和低位，这样能够高效地计算它们的Montgomery约减的值.本文的AVX2 实现将一些常用的代码段通过macro封装起来，这使得整体代码简洁和可读性强.

5.4 常数时间实现

计时攻击[31]是一种常见的侧信道攻击，它指的是敌手可以根据密码方案在软硬件环境中的执行时间等信息来推断所执行的运算操作和内容访问情况，继而攻击者可以根据所获取的侧信道信息来推算出该操作所涉及的一些秘密信息，如私钥或者一些秘密值.目前来说，密码方案的实现几乎都需要考虑计时攻击，并应该采用常数时间实现策略.因此，本文的LTRU 实现过程采用了常数时间实现策略.最重要的是，本文并没使用非常数时间的指令来操作秘密数据，以及没使用依赖于秘密数据的判断分支语句，也没访问依赖于秘密数据寻址的内存地址.计算NTT 过程中取模使用到的Barrett 约减算法和Montgomery 约减算法均是常数时间实现[59]，且算法本身对任意合适的模数均成立.至于采样秘密多项式f′,g,r，本文均以常数时间的方式来采样.每次固定使用4 b 来生成1 个多项式系数.显然，生成秘密多项式的时间也是恒定的.

6 比较和分析

本节将比较混合基NTT 算法与未使用1-迭代Karatsuba 算法和单位根的性质优化乘法数量的NTT算法，以及比较本文LTRU 和其他NTRU 类型密钥封装方案如NTRU-HRSS[20]，SNTRU Prime[21]，NTTRU[26]，NTRU-A[27]，CTRU[28]，BAT[29]，还有基于模格的密钥封装方案如NІST 标准化方案Kyber[22].

表2 给出了混合基NTT 算法与未使用1-迭代Karatsuba 算法和单位根的性质优化乘法数量的NTT算法在理论乘法复杂度分析和具体实现的CPU 周期数的比较.

Table 2 Comparison Between Mixed-Radix NTT and Unoptimized NTT表2 混合基NTT 和未优化的NTT 的比较

表3 和表4 展示了本文LTRU 和其他方案对比的详细情况.为方便比较，在此选取与这些方案安全强度接近的参数集，但CTRU 和Kyber 并没有接近128 b量子安全强度的参数集，所以在此选取它们的推荐参数集.SNTRU Prime 选取SNTRU Prime-761 参数集，NTRU-A 选取参数集，CTRU 选取CTRU-768 参数集，BAT 选取BAT-512 参数集，Kyber 选取Kyber-768 参数集.其中NTRU-HRSS，SNTRU Prime-761，Kyber-768 的数据和开源代码来自它们的NІST第3 轮材料.NTTRU 的数据和开源代码来自文献[26].的数据来自文献[27]，CTRU-768 的数据来自文献[28]，BAT-512 的数据来自文献[29].

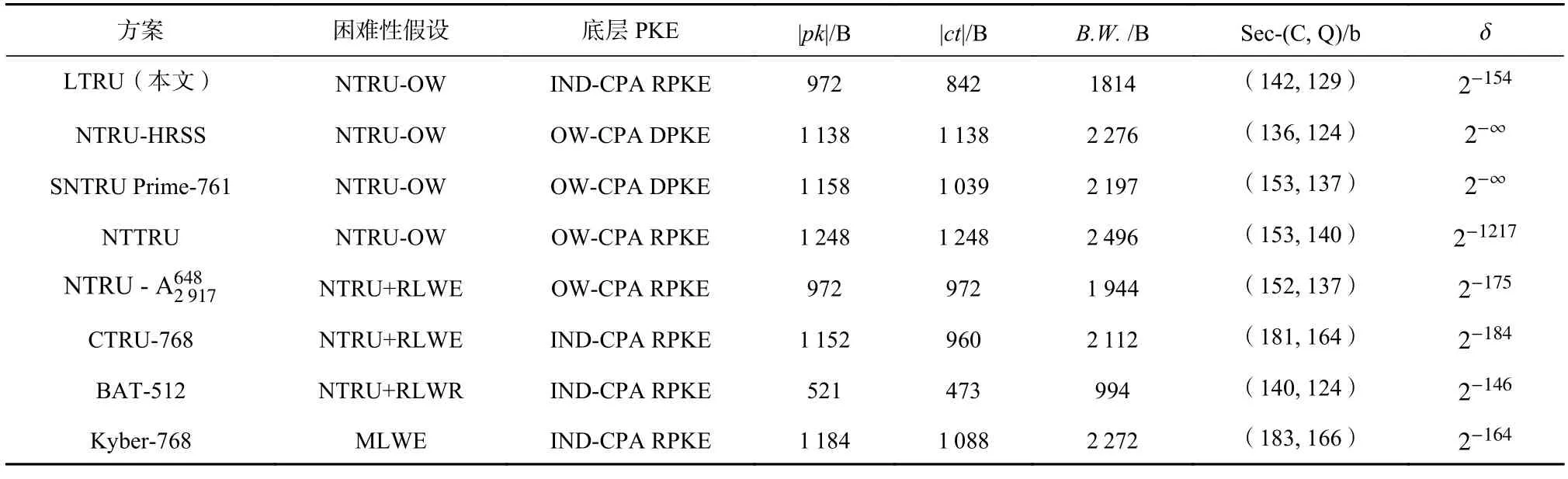
Table 3 Comparison Between LTRU and Other Schemes表3 LTRU 和其他方案的对比

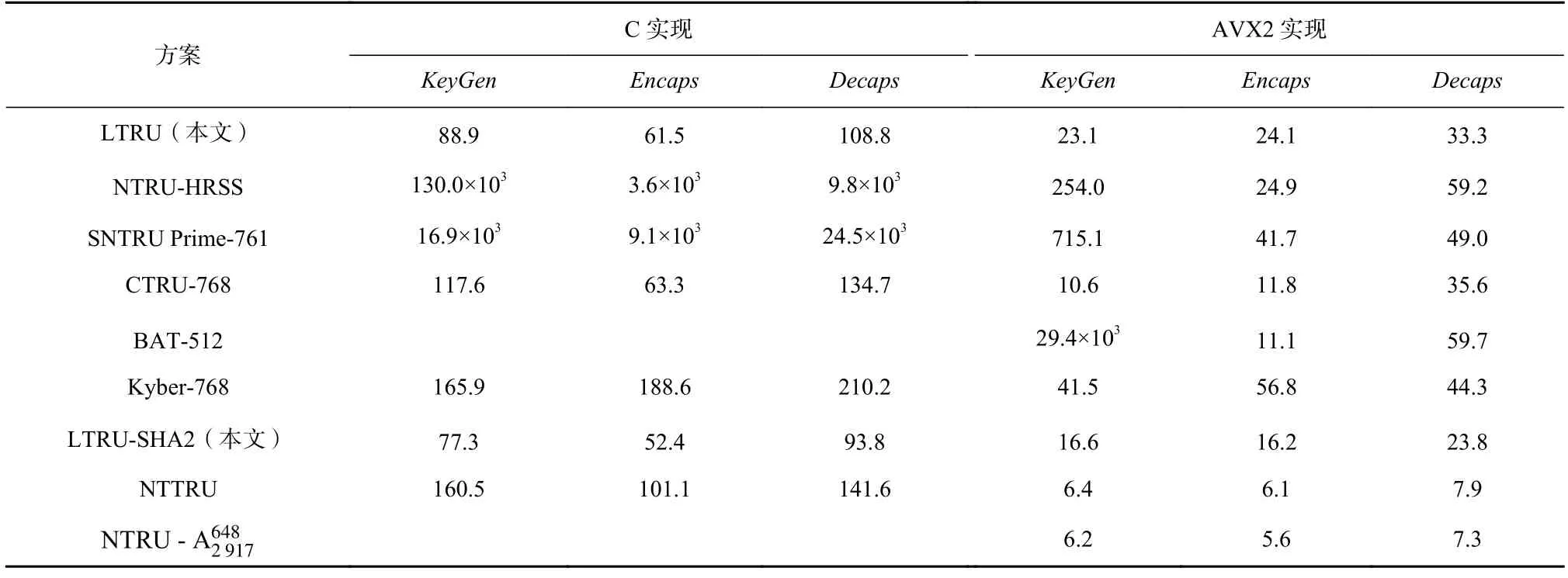
Table 4 Comparison of Implementation Efficiency of Schemes表4 方案的实现效率对比 kcycle

6.1 NTT 算法的比较

值得注意的是，本文的混合基NTT 和未优化的混合基NTT 在多项式环 Zq[x]/(xn-xn/2+1)首层CRT同构具有相同的乘法复杂度：正向变换时需要n/2个乘法，逆向变换时需要 3n/2个乘法.为方便比较乘法复杂度，在此记基-2 FFT trick 和基-3 FFT trick 的层数分别为l2和l3.在本文的混合基NTT 中，每层基-2 FFT trick 的正向变换和逆向变换均需要n/2个乘法.每层基-3 FFT trick 的正向变换和逆向变换均需要n个乘法.然而，未优化的NTT 每层基-3 FFT trick 的正向变换和逆向变换均需要 2n个乘法.因为2 种NTT 算法的求逆运算相同，于是求逆运算具有相同的乘法复杂度，故可以省去对它们的求逆运算的比较.

从表2 可以看出，在比较多项式乘法复杂度时，本文NTT 比未优化的NTT 在正向变换、点乘和逆向变换方面分别减少了nl3，n/2，nl3个乘法，总计减少2nl3+n/2 个乘法.具体而言，选取参数n=648和q=2 917 时，此时层数分别为l2=1,l3=4.测试数据均由C 语言实现，并采用O3 优化指令.从具体实现的CPU 周期数来看，相比未优化的NTT，本文NTT在正向变换、点乘和逆向变换的CPU 周期数分别降低24.9%，20.6%，26.8%，总共降低25.3%.

6.2 方案的性能比较

在表3 中，困难性假设指的是该方案所基于的困难性问题.底层PKE 指的是该密钥封装方案所蕴含的底层公钥加密方案的属性，其中ІND-CPA 指不可区分意义下的选择明文安全性，OW-CPA 指单向意义下的选择明文安全性，DPKE 指确定性的公钥加密方案，RPKE 指随机性的公钥加密方案.|pk|，|ct|，B.W.分别指它们的公钥尺寸、密文尺寸和带宽（公钥尺寸+密文尺寸），单位均是 B.Sec-（C,Q）是方案的安全强度，C 表示经典安全强度，Q 表示量子安全强度.δ指方案的错误率.

6.3 方案的效率比较

在表4 中，KeyGen，Encaps，Decaps对应的列分别给出这些密钥封装方案在密钥生成算法、密钥封装算法和解封装算法运行10 000 次的平均CPU 周期，单位是kcycle.

需要说明的是，NTRU-HRSS，SNTRU Prime-761，NTTRU，Kyber-768 的C 实现数据均是将它们的开源C 代码在同一平台上运行得到的，旨在为它们的C 实现效率提供直观的对比.至于NTRU-HRSS，SNTRU Prime-761，Kyber-768 的AVX2 实现的测试数据则是取自SUPERCUP（代号为supercop-20220506，测试设备为3.0GHz Іntel Xeon E3-1 220 v6）[60]；SUPERCUP能够提供密码方案的AVX2 实现最新最快的测试数据.NTTRU 的AVX2 测试数据取自文献[26].NTRU-的AVX2 测试数据则取自文献[27]，BAT-512 的AVX2 测试数据则取自文献[29]，CTRU-768 的C 实现和AVX2 实现的测试数据均是取自文献[28].需要注意的是，文献[27-28]没有提供开源C 代码和AVX2代码，文献[29]只提供AVX2 代码.且文献[27,29]只提供AVX2 实现的测试数据，故为公平比较，表4 只展示和BAT-512 的AVX2 实现的测试数据，而不再展示它们的C 实现的测试数据.

6.4 分析和结论

经表3 和表4 的数据分析，与其他基于NTRU 格的密钥封装方案NTRU-HRSS[20]，SNTRU Prime[21]，NTTRU[26]，NTRU-A[27]，CTRU[28]，BAT[29]，还有基于模格的密钥封装方案Kyber[22]相比，本文的LTRU 具有4 点优势：

1）小的公钥尺寸、密文尺寸和带宽

与NTRU-HRSS，SNTRU Prime-761，NTTRU，CTRU-768，Kyber-768 对比，LTRU 具有更小的密文尺寸和更小的通信带宽.具体地，与NTRUHRSS 对比，LTRU 的公钥尺寸降低14.6%，密文尺寸降低26.0%，带宽降低20.3%.与SNTRU Prime-761 相比，LTRU 的公钥尺寸降低16.1%，密文尺寸降低19.0%，带宽降低17.4%.与Kyber-768 相比，LTRU 的公钥尺寸 降低17.9%，密文尺寸降低22.6%，带宽降低20.2%.LTRU 和具有相同长度的公钥尺寸，但是LTRU 的密文尺寸更小，降低了13.4%.由于BAT-512 使用复杂的纠错码使得它能使用更小的模数，从而它的带宽比LTRU 的更有优势，但复杂的纠错码导致它的密钥生成比LTRU 的密钥生成慢了3个数量级.

2）均衡的安全强度、错误率和带宽

由于LTRU 的目标安全强度为128 b，所以它的错误率 2-154可视为可忽略.NTRU-HRSS 和BAT-512的量子安全强度只有124 b，并没达到128 b.而Kyber-768 具有166 b 量子安全强度.CTRU-768 具有164 b量子安全强度，与128 b 的间距过大，造成过剩的安全性.SNTRU Prime-761，NTTRU，虽然达到了128 b 安全强度，但其带宽都比LTRU 的带宽大.注意到NTRU-HRSS 和SNTRU Prime-761 均为零错误率，但是它们需要使用更大的模数q，这无疑增加了通信带宽.所以，与其他方案对比，LTRU 达到了128 b 安全强度，且具有与安全强度匹配的、可忽略的错误率，同时能够节省通信带宽.

3）强的底层PKE 方案安全性

由于Kyber-768 是基于MLWE 困难性假设的，而其他方案都是基于NTRU 相关的困难性假设，所以为了公平对比，在此只比较LTRU，NTRU-HRSS，SNTRU Prime-761，NTTRU，CTRU-768，BAT-512 的底层PKE 方案安全性.从表3 可以看到，LTRU，CTRU-768，BAT-512 的底层PKE 方案能够达到ІNDCPA 安全性，而NTRU-HRSS，SNTRU Prime-761，NTTRU，的底层PKE 方案均是OW-CPA 安全的.其中CTRU-768 和BAT-512 均基于2 个困难性假设，唯有LTRU 仅基于NTRU-OW 假设而达到ІND-CPA安全性.不容忽视的是，对底层PKE 方案来说，ІNDCPA 安全性比OW-CPA 安全性更强.

4）高效的实现

从表4 可知，LTRU 具有出色的实现效率.具体而言，与NTRU-HRSS 的C 实现相比，LTRU 在密钥生成、封装和解封装等算法上分别快了1 462.3 倍、58.5 倍和90.0 倍；与NTRU-HRSS 的AVX2 实现相比，LTRU在密钥生成算法和解封装算法上分别快了10.9 倍和1.7 倍，其封装算法的速度与NTRU-HRSS 的相当.另外，与SNTU Prime-761 的AVX2 实现相比，LTRU 在密钥生成、封装和解封装等算法上分别快了30.9 倍、1.7 倍和1.4 倍.主要原因是LTRU 使用了本文提出的高效的混合基NTT 计算多项式运算，而NTRUHRSS 和SNTU Prime-761 使用的多项式环不是NTT友好的，它们只能使用效率更低的算法计算多项式运算.与CTRU-768 相比，LTRU 的C 实现在密钥生成、封装和解封装等算法都更有优势，AVX2 实现在解封装算法的速度与CTRU-768 的相当.与BAT-512 的AVX2 实现相比，LTRU 在密钥生成算法上快了3 个数量级，在解封装算法上快了1.7 倍.

与Kyber-768 相比，LTRU 的实现效率全面占优.具体而言，与Kyber-768 的AVX2 实现相比，LTRU 在密钥生成、封装和解封装等算法上分别快了1.7 倍、2.3 倍和1.3 倍.这得益于LTRU 在密钥生成算法中使用高效混合基NTT 以及在加密和解密算法中只需要计算1 个多项式乘法.然而，Kyber 在密钥生成算法和加密算法中均需要使用拒绝采样生成矩阵且需要计算多项式矩阵-向量乘法，其中解封装算法中还有重加密和重新计算多项式矩阵-向量乘法的过程，这些操作明显更加耗时.与之对比，LTRU 方案具有运算简单、实现高效等特点.

7 总结

基于NTRU 格的密码系统具有结构简洁、强安全保障、不受专利影响等优势，有利于设计实用化高效的后量子密码方案.本文提出了一个仅基于NTRU 单向困难性假设构造的、不使用纠错码也能够压缩密文的密钥封装方案LTRU.LTRU 包含一个ІND-CPA 安全的公钥加密方案LTRU.PKE 以及一个ІND-CCA 安全的密钥封装方案LTRU.KEM.本文还提供了针对128 b 安全强度的参数集，及其对应的C 实现和AVX2 实现.针对LTRU 所使用的环Z2917[x]/(x648-x324+1)上的多项式乘法和除法，本文提出了一种高效的混合基NTT 算法，该算法结合单位根的性质和1-迭代Karatsuba 算法来减少乘法的数量，以提高计算效率.本文实验结果表明，与NІST 标准化方案Kyber-768 相比，LTRU 的公钥尺寸降低17.9%，密文尺寸降低22.6%，带宽降低20.2%；与NІST 第3 轮决赛方案NTRU-HRSS 相比，LTRU 的经典安全强度和量子安全强度分别增强6 b 和5 b，以及公钥尺寸降低14.6%，密文尺寸降低26.0%，带宽降低20.3%，并且LTRU 的实现效率优于NTRU-HRSS.

未来工作主要包括2 点：1）对本文提出的LTRU在多平台上实现，包括ARM Cortex-M4 实现和FPGA实现等；2）提出更多的LTRU 参数集，使其满足更多的应用场景，如资源受限的ІoT 设备和智能卡等.

作者贡献声明：梁志闯负责方案的设计和论文撰写；郑婕妤负责方案的实现；赵运磊负责论文修改.