基于弥散颗粒燃料的先进核反应堆大规模并行模拟与优化

李睿涵 侯叶凡 李玉辉 刘召远 张海红 梁金刚

1（清华大学核能与新能源技术研究院 北京 100084）

2（齐鲁工业大学（山东省科学院） 济南 250353）

（li-rh20@mails.tsinghua.edu.cn）

随着能源和环境问题日益严峻，社会亟需发展区别于传统化石能源的新能源.其中，核能由于其稳定性好、能量密度大、碳排放量低的优点而成为解决能源与环境问题的有力手段.此外，由于以上优点，核能还是航天器、潜艇、水面舰艇等特种设备的良好供能方式.因此，核能存在着较大的发展机遇.

由于核能实验研究成本较高，故计算机模拟计算成为了核能领域的重要研究方式.其中，以反应堆堆芯核反应率分布为主要研究对象的“反应堆物理”计算有助于获得反应堆有效增殖因数（keff）、功率分布等关键参数，并为堆芯热工计算、核电厂系统计算等其他模拟研究提供必要的参数，是核能模拟计算研究的重要组成部分.蒙特卡罗（Monte Carlo，MC）方法[1]是使用计算机生成随机数来模拟中子等微观粒子在堆芯内的运动、散射、吸收等随机行为的计算方法，其数学模型较为贴近堆芯实际的物理过程，故计算结果较为精确.但同时MC 方法需要对堆芯的大量粒子分别进行模拟，因此也存在着计算量大的缺点.而由于堆芯中各粒子的行为是相对独立的，故MC 方法可以将不同粒子直接分配给不同线程（进程）进行计算，这样的并行模式天然具有非常好的并行可扩展性，与之相比，基于区域分解的并行模式的并行效率随并行规模的增加而显著降低[2]，因此是一种非常适合并行计算的方法.目前，MC 方法已经在反应堆物理计算领域得到了广泛地应用[3-6].

当前，随着核技术的发展，一种新型的核燃料：颗粒燃料逐渐得到了越来越广泛的应用.诸如球床式高温气冷堆[7]、空间反应堆[8]、氟盐冷却高温堆[9]、耐事故燃料[10]等多种先进核能装置中均使用了这种燃料.颗粒燃料是将核燃料活性成分，例如UO2制成小颗粒，然后弥散在基体中，而非传统棒状燃料使用整块均匀的UO2.可见，颗粒燃料的使用必将导致堆芯几何中存在大量随机球体.以一种高温气冷堆HTRPM（high-temperature gas-cooled reactor pebble-bed module）为例，其堆芯存在约42 万个随机堆积的球形燃料元件，每个燃料元件中又包含约1 万个随机排列的燃料颗粒[7]，如图1 所示，因此其全堆总共存在约40 亿个随机排列的球体.如此复杂的几何结构会为反应堆物理计算，尤其是MC 计算带来极大的困难，大大增加其计算耗时.例如经本文验证，在相同的MC 计算规模（即模拟的中子数量，根据统计学大数定律，计算的中子数越多，结果越精确，标准差越小）以及并行规模下，如果不使用任何加速方法，一个HTR-PM 的球形燃料元件的计算耗时将达到一个传统压水堆棒状燃料元件的400 倍以上.因此有必要开展适用于颗粒燃料几何的加速方法研究.

本文以其中几何较为复杂的球床式高温气冷堆HTR-PM[7]为例，在开源MC 程序OpenMC[11]的基础上进行加速方法的研究.

HTR-PM 是由清华大学核能与新能源技术研究院主导研发的球床式高温气冷堆，具有第4 代先进核能系统[12]特征.因其具有良好的固有安全性，HTR-PM受到了学界的广泛认可.其示范堆山东石岛湾核电站属于我国16 个国家科技重大专项之一，目前已经完成了建设并实现了并网发电.因此，针对HTR-PM的研究将具有很高的工程应用价值.

OpenMC 是由美国麻省理工学院主导开发的开源MC 中子输运程序.除麻省理工学院外，阿贡国家实验室、密歇根大学等多个研究机构也对其开发工作做出了贡献.OpenMC 程序具有较高的几何建模和数据统计灵活性，并具备高性能并行能力，支持MPІ（message passing interface）和OMP（open multi-processing）混合并行.作为开源程序，OpenMC 自2011 年问世以来已经在世界范围内进行了大量的反应堆物理计算，其各项功能得到了学界的充分验证，具有较高的可靠性.因此OpenMC 适合用于开展本项研究.

除HTR-PM 外，本文还建立了一种使用颗粒燃料的空间反应堆模型，以对优化后的程序进行辅助验证.

1 模型建立

1.1 随机球体位置的生成

为建立颗粒燃料的高精度模型，必须准确设定每个燃料颗粒的位置.对于HTR-PM 中的数十亿燃料颗粒来说，通过实验方法测量其位置显然是不现实的，因此颗粒的位置也必须通过计算机模拟计算得出.

OpenMC 程序本身具备生成随机颗粒位置的功能.其使用的是RSP（random sequential packing）和CRP（close random packing）结合的方法[13].RSP 是在规定的空间内随机选取球体位置并去除重叠的球体的方法.这一方法在填充率较低时拥有较高的计算效率，但其无法生成38%以上填充率的随机颗粒，且其生成的颗粒是均匀分布在空间内的，无法模拟重力作用下的球堆.CRP 方法则可以生成填充率更高的随机颗粒，但其计算效率较低，同时也无法模拟重力的影响（由于本文不涉及CRP 方法，故对其原理不再赘述）.OpenMC 在生成随机颗粒时，会根据目标填充率进行判断，如果填充率较低，则使用RSP 方法，否则将使用CRP 方法.除此之外，OpenMC 还支持用户从外部输入颗粒的位置，为其与其他程序的耦合提供了可能.

HTR-PM 堆芯中包含2 重随机球体，首先是堆芯容器中堆积的燃料球，其次是每个燃料球中弥散的燃料颗粒，如图1 所示.在建立OpenMC 模型时，可以首先建立单个燃料球及其内部的燃料颗粒的模型，然后使用“重复结构”功能将该燃料球重复地堆积在堆芯容器内.如此一来，HTR-PM 模型中的随机球体就分为了“堆芯容器中的燃料球”和“每个燃料球中的燃料颗粒”2 部分.因此建模时无需生成一个40 亿量级的球堆，而只需生成一个40 万量级和一个1 万量级的球堆即可.对于单个球内的燃料颗粒，其填充率约为7%，且均匀分布在燃料球基体中，因此非常适合使用OpenMC 自带的RSP 方法.而燃料球则是在重力的作用下堆积在堆芯容器内，且填充率约为61%，因此不适合直接使用OpenMC 进行计算，而需要单独进行处理.

本文使用了DEM（discrete element method）程序LAMMPS[14]来生成燃料球的位置信息.DEM 方法是使用经典力学模拟每个颗粒运动过程的方法.在LAMMPS 模型中，首先设置好堆芯容器的几何，然后在高处生成燃料球，再令其在重力作用下自然下落并堆积在容器内即可.由于这一物理模型较为接近HTR-PM 的实际装料过程，因此可以得到较为准确的结果.LAMMPS 模型的具体参数与文献[15]中的一致.

值得一提的是，HTR-PM 模型并非包含42 万个燃料球的平衡堆芯模型，而是包含约5 万个燃料球和28 万个石墨球的初装堆模型[16]，这是因为当前HTRPM 示范堆山东石岛湾核电站投产不久，并未达到平衡堆芯状态，而仅有初装堆的运行数据.因此，建立初装堆模型可以与石岛湾核电站的实验数据进行对比，以更加有力地验证程序的准确性.

初装堆状态下，堆芯的燃料球和石墨球并非均匀混合，而是先在堆芯底部堆积约23 万个石墨球，然后在其上方混合堆积约5 万个燃料球和5 万个石墨球.由于LAMMPS 程序只关注球的经典力学特征，不关注其核物理性质，而燃料球和石墨球的经典力学特征，如质量、摩擦系数、弹性系数等相近，因此这2 种球在LAMMPS 模型中不作区分.在LAMMPS给出球的位置后，再人工确定其中哪些是石墨球、哪些是燃料球，最后将数据输入到OpenMC 中.

LAMMPS 程序得出的球床堆积率为61%，与文献[16]中的符合较好.

与HTR-PM 不同，本文模拟的空间反应堆[17]堆芯为包含1 519 个圆形冷却剂孔道的六棱柱，其几何中仅存在1 种随机球体，即弥散在堆芯固体区域内的大量燃料颗粒.该堆芯中颗粒填充率约为30%，且均匀分布在基体中，因此使用RSP 方法计算即可.但是，由于全堆燃料颗粒数量极多（约3 亿个），故直接使用OpenMC 在整个堆芯内部随机生成颗粒位置是不实际的，此外OpenMC 还不支持在带有冷却剂孔道的复杂几何中生成随机颗粒位置.综上所述，本文在建立空间堆模型时同样使用了“重复结构”功能：将一个冷却剂孔道周围的六棱柱区域视为一个单元，使用RSP 方法在此实心六棱柱内部随机生成燃料颗粒，并人工去除生成在冷却剂孔道中的颗粒位置，然后将1 519 个这样的单元重复填充在堆芯中，即可实现空间堆随机颗粒的建模.

1.2 HTR-PM 与空间堆全堆模型

在1.1 节所述的生成随机颗粒位置方法的基础上，本文根据石岛湾核电站初装堆相关参数[16]，建立了HTR-PM 堆芯的OpenMC 模型，如图2 所示.并根据文献[17]建立了空间堆堆芯的OpenMC 模型，如图3 所示.

Fig.2 OpenMC model of the HTR-PM core图2 HTR-PM 堆芯的OpenMC 模型

Fig.3 OpenMC model of the space reactor core图3 空间堆堆芯的OpenMC 模型

2 加速方法

2.1 网格加速的原理

前文已经提到，大量随机球体的几何结构会大大增加MC 方法的计算量.究其原因，是程序无法对随机排列的球体进行有效地检索.例如在图4（a）所示的情形中，大量随机排列的燃料颗粒空间中存在一个中子，而程序需要确认中子具体位于哪个颗粒内.为此，程序只能将中子的坐标一一带入颗粒的几何信息中进行验证，如式（1）所示：

Fig.4 Basic principle of lattice speed up图4 网格加速的基本原理

其中r0是中子位置，ri是第i个燃料颗粒的球心位置，Ri是第i个燃料颗粒的半径.如果对于某一燃料颗粒i，式（1）得到满足，则中子位于该颗粒内或其表面，而如果中子不位于任何燃料颗粒内，则中子位于基体中.

显然，由于模型中颗粒的数量极多，以上“遍历所有颗粒”的过程必然耗费大量时间，因此有必要进行优化.

针对这一问题，“网格加速”方法是一种有效的手段.如图4（b）所示，在空间中划分规则的网格，使得每个单元格的范围为

其中，(x0,y0,z0) 为网格空间角点坐标；Px，Py，Pz分别为x，y，z方向的网格栅距；i，j，k分别为x，y，z方向的网格编号.

完成网格划分后，即可建立单元格与燃料颗粒的对应关系，将与某单元格相交的所有燃料颗粒的几何信息与该单元格编号 (i,j,k)关联（该过程仅在程序初始化时进行，计算过程中无需重复）.如此，则当进行中子位置的判断时，程序即可首先根据式（2）求出中子所在的单元格 (i,j,k)，然后仅遍历该单元格内的所有燃料颗粒即可.例如图4（b）所示的情形中，只需对3 个实线的燃料颗粒进行验证，而无需验证虚线的颗粒，这就大大节省了计算时间.以上即为网格加速方法的基本原理.

2.2 虚拟网格与真实网格

当前OpenMC 中已经支持网格加速方法，但其使用的是“真实网格”，而本文为OpenMC 添加的是“虚拟网格”的方法，本节将介绍二者的不同.

在真实网格模型中，网格分界面是模型中真实存在的曲面，模型将被网格面划分为若干长方体.如图5（a）所示，使用真实网格方法将模型划分为左右2 个单元格，则最终的模型是由左右2 个长方体拼接而成的.

Fig.5 Division patterns of different lattices图5 不同网格的划分方式

而虚拟网格则是一套假想的网格，其模型几何中不存在网格面，不会对模型进行分割.如2.1 节所述，网格加速方法本质上是建立一种各球体与其所在区域的对应关系，以便根据粒子位置缩小所需遍历的球体数量.因此，网格面的存在是没有必要的，只需按照网格位置对各球体进行编号即可.例如图5（b）所示的情形下，使用虚拟网格划分模型，则只需对左侧4 个球体添加编号“1”，代表其属于左侧单元格；对右侧4 个球体添加编号“2”，代表其属于右侧单元格；对中间球体同时添加编号“1，2”，代表其同时属于2 个单元格.模型的几何不存在变化.

虚拟网格方法与真实网格相比，具有4 个优点：

1）虚拟网格对存储空间的占用更小.这是因为真实网格的模型几何由大量的单元格几何体拼接而成，其复杂度远超虚拟网格模型的单一几何体.以图2所示的HTR-PM 堆芯模型为例，为达到良好的加速效果，需要做出较细的网格划分，例如将堆芯容器内堆积的燃料球以及石墨球划分为33×33×154 的网格，同时将单个燃料球内的燃料颗粒划分为24×24×24 的网格.显然，如果使用真实网格，则如此大规模的单元格必将占据大量存储空间.表1 展示了该网格划分下虚拟网格与真实网格模型占用的存储空间对比，可见使用虚拟网格方法将大大节约存储空间.

Table 1 Storage Space Occupation of HTR-PM Model表1 HTR-PM 模型存储空间占用

2）虚拟网格的计算速度更快.具体表现在2 方面.①在程序初始化阶段，虽然虚拟网格模型需要额外对球体进行编号，但由于其模型几何大大简化，使得初始化的整体耗时远小于真实网格模型.②在程序计算阶段，由于虚拟网格模型不存在网格面，故程序无需对中子穿过这些网格面的过程进行模拟，因此虚拟网格模型也将在计算阶段节约时间.表2 展示了相同计算规模和并行规模下，HTR-PM 堆芯模型的计算时间对比.可见虚拟网格模型的初始化时间和计算时间分别约为真实网格模型的13%和82%，拥有更高的计算效率.

Table 2 Time-Consumption of HTR-PM Model表2 HTR-PM 模型计算耗时 s

表3 则展示了空间堆模型的计算时间对比，其虚拟网格的初始化时间和计算时间分别为真实网格的13%和46%，与HTR-PM 模型相比效率的提升更为明显.

Table 3 Time-Consumption of the Space Reactor Model表3 空间堆模型计算耗时 s

3）虚拟网格的数据统计更加便捷.由于真实网格模型存在网格面对模型进行分割，其难免会切断模型中随机分布的球体，使得一个完整的球在模型中实际由2 个，甚至多个“半球”拼接而成.例如图5（a）中，中间的球体被网格面分割为了2 部分.因此如果用户需要以单个球为单位统计某参数（例如功率分布），其必须人工将多个“半球”指定为一个整体进行统计，这为用户操作带来了困难.而虚拟网格模型中不存在网格面，其所有球均为一个完整的球体，因此用户可以便捷地进行数据统计.

4）使用虚拟网格加速的模型拥有更好的并行可扩展性.这是因为虚拟网格模型几何更简单，使得单个中子输运过程的耗时更短、随机性更小.由于在并行计算中，程序只有在每个进程各自完成其“负责”的全部中子的计算后，才会进入下一阶段，故更小的随机性就意味着进程间相互等待的时间更短，即程序拥有更好的负载均衡.图6（a）展示了HTR-PM 虚拟网格和真实网格的并行强可扩展性对比，其中每代中子数保持10 752 000 不变，总代数为20，并行规模为112～10 752 核；图6（b）为弱可扩展性对比，其中每代中子数为核数的1 000 倍，总代数为20，并行规模为112～131 600 核.本文针对图6 的每个数据点均进行了10 次重复测量，并标出了其平均值以及10 次测量结果的变化范围.其中某次测量的并行效率是用测量得到的计算时间与基点（112 核）下10 次测量的平均时间计算得出的.由于数据的波动性，某些“并行效率”可能超过了100%.

Fig.6 The parallel scalability comparison of the virtual lattice and physical lattice图6 虚拟网格与真实网格并行可扩展性对比

可见，在强扩展问题中，当并行规模达到约3 000核时，虚拟网格的并行效率显著高于真实网格；而对于弱扩展问题，当并行规模达到约3 000 核时虚拟网格的并行效率略高于真实网格；而达到约10 000 核时该趋势则更为显著.因此可以认为虚拟网格拥有更好的并行可扩展性.此外，真实网格测量结果的波动范围明显远大于虚拟网格，这可能是因为真实网格数据量更大、中子历史更复杂，其在缓存读写等方面具有更大的不确定性.

2.3 虚拟网格加速在OpenMC 程序的实现

在OpenMC 程序中，首先需要对初始化部分进行修改，以便生成虚拟网格.具体的方法为：根据式（2）的规则建立单元格编号与其位置的对应关系，并建立对应的3 维数组，使得数组编号与单元格编号一一对应.然后对于每一个单元格，遍历所有随机球体，如果某一球体与单元格存在交集，则程序将该球的信息，包括其编号、球心位置、半径储存在单元格对应的数组元素内.在对所有的单元格完成遍历后，就成功建立了燃料颗粒的几何信息与单元格编号的关联，即生成了虚拟网格.

除生成虚拟网格外，还涉及计算过程中对虚拟网格的利用问题，需要对OpenMC 进行修改.

OpenMC 计算中的几何处理过程包含3 项主要任务：

1）已知中子的位置，求其位于哪个几何体内；

2）已知中子的位置及其运动方向和运动距离，求其即将与哪个曲面相撞；

3）已知中子正在穿过某一曲面，求其即将进入哪个几何体.

其中，任务1 已经在2.1 节中进行了讨论，此处不再赘述.

对于任务2，由于任意曲面都可以表示为f(x,y,z)=0，因此在已知中子当前位置r0和其运动方向rdir（单位向量）后，只需求解关于运动距离l的方程：

即可求得中子运动到该曲面上所需的距离，如果方程没有正实数解，则中子不会与该曲面相撞，此时程序会将碰撞距离l记为正无穷.在模型空间的所有曲面中，l值最小的曲面即为即将与中子相撞的曲面.此处值得一提的是，假如最小相撞距离大于中子本次运动的距离，则中子不会与任何曲面碰撞，而是会在当前所处的几何体内发生核反应.

可见，这项任务的计算量同样会受到遍历的曲面数量的影响.在大多数情形下，所需遍历的曲面数量不多，无需进行优化，而当“中子位于基体内，求其即将与哪个球体相撞”时，需要对所有球面进行遍历，其计算量过大，需要借助虚拟网格加以简化.简化的方法与任务1 类似，程序首先可以根据中子的位置找出中子所在的单元格，然后仅遍历该单元格内的所有球面即可，如果这些球面均不满足碰撞要求，则只需对下一个单元格内的球面进行遍历，如此循环直至找到即将碰撞的球面，这样就有效减少了需要检验的曲面数量.

任务3 的逻辑则较为简单.在中子穿过曲面离开某几何体时，程序只需遍历与该几何体相邻的所有几何体，判断中子是否在其内部即可.但这一过程同样存在计算量问题：当中子穿过球体表面进入基体时，程序需要判断中子是否在基体空间内，这需要对组成基体空间的大量曲面（这些曲面包括基体内的所有球面）一一进行验证，极为耗时.而实际上这一过程是没有必要的，中子穿过球体表面离开球体时必然会进入基体.因此本文针对这种特殊情况进行了优化，取消了其判断过程，直接认定中子进入了基体，即可显著减小计算量.

表4 展示了在56 个进程的纯MPІ 并行下，对于高温气冷堆单个燃料球模型（中子历史为100 代，每代1 万个）使用不同优化水平时的计算耗时对比.可见对3 项任务的优化均可使计算效率得到明显提升.值得一提的是，如果使用真实网格方法对该模型进行加速，其计算耗时为65 s，可见其计算耗时高于虚拟网格方法.

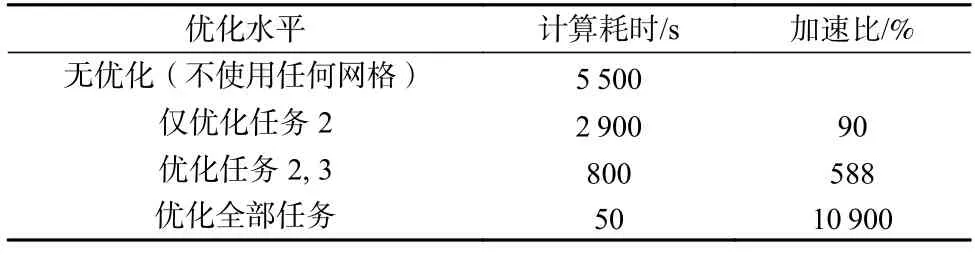
Table 4 Comparison of the Time-Consumption of Single Pebble Model in HTR-PM Under Different Virtual Lattice Optimizations表4 不同虚拟网格优化下HTR-PM 单个燃料球模型计算耗时对比

而对于HTR-PM 全堆模型（中子历史为1 000 代，每代10 万个），在相同并行规模下（10 个MPІ 进程，每个进程56 个OMP 线程）与不进行优化相比，优化全部任务后其计算耗时可以从估算耗时约10 700 h 减小到539 s，计算效率大幅度提升，加速效果更为显著.

3 结果分析

3.1 程序运行环境

本文所做的计算均在国家超级计算济南中心的山河超级计算平台开展，其采用Іntel Xeon 6258R 型号28 核CPU 处理器，主频2.7 GHz，每个计算节点包含2 个CPU，其内存为192 GB.使用的操作系统为Linux version 3.10.0-957.el7.x86_64，编译所用的软件为cmake/3.21.1，gcc/9.4.0，hdf5/1.8.13，mpich/3.4.2.

需要特别指出的是，表1 所示真实网格算例的内存占用（213 GB）超过了山河超算平台单个节点的内存，该算例实际是在北京超算平台测试的.而本文其他真实网格模型则略微缩小了网格规模，使其能够在山河平台运行.

3.2 计算结果分析

本节将介绍HTR-PM 和空间堆模型的定量化计算结果，以验证优化后程序的性能及其正确性.

有效增殖因数（keff）可以描述核反应堆的临界程度，是衡量反应堆物理计算结果的重要指标.山东石岛湾核电站于2021 年成功临界，其临界时keff=1.而本文按照其参数建立的HTR-PM 虚拟网格模型的keff计算结果为0.998 54±0.000 10，二者相差146 pcm.同时，如果使用OpenMC 程序本身的真实网格方法计算，则其keff=0.998 51±0.000 10，与虚拟网格仅相差3 pcm.可见，无论是与实验值对比，还是与OpenMC 程序本身对比，HTR-PM 虚拟网格模型的结果都符合得很好.

而本文模拟的空间堆还处于理论阶段，不存在相应实验装置.同时，文献[17]并未对空间堆燃料颗粒进行显式建模，而是将材料混合后建立了均匀燃料模型.研究表明，这样的处理方法会使计算结果存在很大偏差[18-20]，不具有参考价值.综上所述，本文的空间堆虚拟网格模型缺少实验或计算结果作为验证基准，因此其只能与OpenMC 自身的真实网格方法进行对比验证.经计算得到：虚拟网格模型的计算结果为keff=1.105 47±0.000 07，真实网格的结果为keff=1.105 51±0.00007，二者符合较好.

综上所述，可以认为使用虚拟网格优化后的程序具有良好的准确性.图7 展示了HTR-PM 的堆芯功率分布，其中白球为石墨球，无功率.得益于2.2 节所述的虚拟网格数据统计方面的便利性，该功率分布结果可以精确到单个燃料球.

Fig.7 Power distribution of the HTR-PM core图7 HTR-PM 堆芯功率分布

图8 展示了空间堆模型的堆芯径向功率分布，结果可精确到全堆尺寸的1/8000.

Fig.8 Power distribution of the space reactor core图8 空间堆堆芯功率分布

3.3 并行性能分析

3.3.1 并行策略优化

OpenMC 支持MPІ 和OMP 混合并行，而在并行总核数相同的情况下，不同的MPІ 进程数和OMP 线程数搭配得到的计算效率不同.因此，有必要寻找一种最优的并行策略.表5 展示了同样使用单节点56核并行的情况下，HTR-PM 虚拟网格模型在不同线程、进程数搭配时的计算时间，其中每种搭配分别测量了10 次结果，计算了其平均值、标准差.

Table 5 Comparison of the Time-Consumption of HTRPM Model with Different Parallel Strategies表5 不同并行策略下HTR-PM 模型计算耗时比较

由表5 可见，当进程数由1 变为2 时，计算效率存在明显提升.这可能和山河超算的硬件条件有关，其单个56 核的节点实际包含了2 个28 核的CPU，因此相比单个进程的设置，2 个进程的设置可以简化CPU 之间的通信，进而节省计算时间.此后随着进程数的增加，计算效率存在先升后降的趋势，这是因为MPІ 并行虽然计算效率更高，但其通信也更为耗时，因此过少或过多的MPІ 进程数设置都不利于获得更高的计算效率.

考虑到相比于“2 个进程、28 个线程”的并行策略，其他设置对效率的提升不显著，且更多的MPІ 进程设置会大量占用节点内存，不利于大规模数据统计，因此本文最终选取的并行策略是：每个节点2 个进程、每个进程28 个线程.

3.3.2 大规模并行效率分析

本文借助山河超算集群对HTR-PM 模型进行了大规模并行计算，测试了其在10 万核规模下的并行性能.图9 展示了HTR-PM 模型的强、弱可扩展性，其计算规模与2.2 节相同：对于强可扩展问题，每代中子数保持10 752 000 不变，总代数为20，并行规模为112～10 752 核（2～192 节点）；对于弱可扩展问题，每代中子数为核数的1 000 倍，总代数为20，并行规模为112～131 600 核（2～2 350 节点）.图9 中统计的“计算时间”是指排除程序初始化以及写输出所用时间后的运行时间.对于每个数据点，本文均进行了10次测量，并选取了其平均值进行分析.

Fig.9 Parallel scalability of HTR-PM virtual lattice model图9 HTR-PM 虚拟网格模型的并行可扩展性

当计算规模不随并行规模变化时，程序在10 752核并行下与112 核并行相比具有83.4%的并行效率，其理想计算时间与实际计算时间分别为46 s 和55 s.而当计算规模与并行规模成正比时，程序在131 600核并行下与112 核并行相比具有83.1%的并行效率，其理想计算时间与实际计算时间分别为46 s 和56 s.可见程序在大规模并行时仍然具有较高的并行效率，其并行可扩展性良好.

此外注意到在弱扩展问题中，当并行规模由14 336核（256 节点）增大到28 672 核（512 节点）时，程序的并行效率突然下降，由95%降为84%，而此后并行效率随并行规模的下降反而不明显.目前分析这一现象可能由MPІ 通信协议的变化引起.OpenMC 程序的通信耗时主要花费在进程间的中子源同步（synchronizing fission bank）上，在弱可扩展问题中，虽然每个进程的中子数是固定的，但进程间所需传递的中子数量仍会随进程总数的增加而不断增大[21].而MPІ 在通信的信息量较大时，通信协议会随数据量有所调整，从而导致计算耗时的阶跃式增加[22].针对这一现象，在后续研究工作中将开展更加深入的分析和测试.

4 总结与展望

本文在开源MC 程序OpenMC 的基础上，开发了适用于颗粒燃料的虚拟网格加速方法.通过构建虚拟网格并对中子输运过程的3 项主要任务进行优化，有效提高了程序的计算效率.该方法的计算耗时不但远低于不使用网格的算例，且与OpenMC 此前的真实网格方法相比，计算耗时也更小.针对HTR-PM模型和空间堆模型，虚拟网格的计算时间分别减小到了真实网格的82%和46%.同时虚拟网格相较真实网格还具有内存占用小、数据统计方便、并行可扩展性好的优点.

在定量化结果方面，HTR-PM 模型的keff计算结果与石岛湾核电站实验值符合较好，因此可以认为程序具有良好的准确性.除此之外，本文还计算了HTR-PM 和空间堆的功率分布，并得益于虚拟网格方法数据统计的便利性，实现了HTR-PM 精确到单个燃料球的堆芯功率分布计算.

最后，本文对优化后的程序进行了大规模并行测试，结果表明：对于强扩展问题，使用虚拟网格加速的HTR-PM 模型在10 752 核并行下与112 核并行相比，并行效率为83.4%；而对于弱扩展问题，程序在131 600 核并行下与112 核并行相比并行效率为83.1%，因此可以认为程序具有良好的并行可扩展性.

本文所建模型及测试更侧重于对程序并行性能的探讨，模型本身的计算并不需要10 万核规模的并行.在此后的研究中，本文优化的程序将可以用于真正需要大规模并行的、更加复杂的模型中，例如带有燃耗的HTR 模型.

同时，本文程序的并行性能仍存在优化空间.例如进行燃耗计算时，OpenMC 在数据读取和输出部分的并行可扩展性较差，导致其占用了大量时间.这些问题均有待进一步的研究.

作者贡献声明：李睿涵负责算法优化的实现与部分模型的建立以及论文的撰写；侯叶凡负责部分模型的建立；李玉辉负责开展大规模并行计算；刘召远指导并行计算工作以及修改论文；张海红指导建模工作；梁金刚指导算法优化以及修改论文.