基于缓存访问模式的C-AMAT 测量方法及其在图计算中的应用

陈炳彰 刘 伟,2 于萧钰

1（武汉理工大学计算机与人工智能学院 武汉 430073）

2（交通物联网技术湖北省重点实验室（武汉理工大学） 武汉 430073）

（chenbingzhang@whut.edu.cn）

大数据时代下，人类社会中大规模与不规律数据信息快速增长，以图结构对这些数据进行存储分析越来越普遍.基于图结构的信息存储方式被广泛应用于人际关系、社交网络分析、社会科学等各个领域，图数据处理变得越来越重要.而目前图应用的主要性能瓶颈就在于其数据访问层面[1]，因此对于图应用在存储器中性能的评估与分析对于相应的硬件开发和算法设计都具有重要意义.

并发式平均存储访问时间（concurrent average memory access time，C-AMAT）模型通过同时考虑存储器访问的局部性和并发性[2]，可以更准确地表征图应用的存储器性能.但是C-AMAT 的计算模型认为数据访问的命中时间总是固定的，存在一定的局限性，同时，又因为其测量装置硬件开销大，使得其在实际应用中是不易实现的.

为了利用C-AMAT 准确地评估检测图应用的存储器性能，我们基于缓存的访问模式将C-AMAT 的计算模型扩展为PC-AMAT（parallel C-AMAT）和SCAMAT（serial C-AMAT），并在此基础上设计并实现了C-AMAT 中纯粹缺失周期（pure miss cycle，PMC）的提取算法及所需各项参数的测量.最终利用CAMAT 在gem5[3]模拟器中对各类图应用在存储器中的性能进行了实验评估与分析，提出了相应的访存优化策略.

本文的主要贡献包括3 个方面：

1）基于缓存的数据访问模式将C-AMAT 的计算模型扩展为PC-AMAT 和SC-AMAT，使C-AMAT 的计算模型与现代计算机中不同层次的存储器访问模式相匹配，从而为更准确地测量和计算应用程序运行过程中对数据的并发式平均存储访问时间提供了理论依据；

2）设计并实现了计算C-AMAT 所需的重要中间参数纯粹缺失周期的提取算法，避免了直接测量所需要的巨大硬件开销；

3）利用相关系数验证了PC-AMAT 和SC-AMAT与ІPC 之间的相关性比C-AMAT 更强，进一步设计了图应用的存储器性能评估实验，通过应用各种规模的图数据集对图应用的访存性能进行了系统性地分析.

1 相关工作

图处理是大数据领域中一类重要的计算方式，在机器学习、路径规划、传染病学、神经网络等领域都有广泛应用.

现实世界的图数据往往呈现出小世界性（smallworld）[4]和无尺度性（scale-free）[5]，稀疏矩阵存储格式是典型的图数据存储格式，尽管有研究表明基于稀疏矩阵的压缩稀疏行（compressed sparse row，CSR）、对角线（diagonal，DІA）[6]等格式存储效率很高，但仍然改变不了图数据访问的不规则性，存储器性能效率低下已经成为图应用发展中最大的性能瓶颈.目前学术界关于图数据处理性能的研究有很多.Basak等人[1]通过分析乱序CPU 下图数据的访存行为发现不同数据类型加载指令之间的依赖链（load-load dependency chain，LLDC）是实现高内存级并行（memory level parallelism，MLP）的主要瓶颈；Balaji 等人[7]在末级缓存（last level cache，LLC）更换不同的数据替换策略时发现，即使是最先进的缓存数据替换策略，图应用在LLC 上的MPKІ（misses per kilo instructions）依然没有明显下降；汤嘉武等人[8]通过实验分析出通用高层次综合（high level synthesis，HLS）系统缺乏对不规则图算法有效支撑的问题，提出了一种面向图计算的高效HLS 方法，实现了高效的并行流水执行；Faldu等人[9]验证了由于图分析的高度不规则访问模式，最先进的硬件缓存管理方案在利用其重用方面依然不尽人意，为此，他们引入了专门用于LLC 上对图分析进行缓存管理的GRASP，GRASP 专用缓存策略利用了热顶点固有的高重用，同时保留了捕获其他缓存块中图数据重用的灵活性；Cooksey 等人[10]则从高速缓存行中获取任何看似合理的地址作为数据加载，但是，只有观察到数据结构是一个指针列表时，这些指针才将被引用，否则此类方案将显著超载，从而导致缓存污染和性能下降.

尽管学术界现有的研究工作从多个维度对图应用进行性能评测都发现了其性能瓶颈在访存层面，但采用的系统性能评估指标更多地停留在以计算为中心的层面，最为广泛使用的便是每周期完成指令数（instruction per clock，ІPC），但ІPC 是被设计用来测试CPU 性能的，并且由于ІPC 受指令集、CPU 微架构、存储器层次结构和编译器技术等多方面的影响，无法直接用来反映存储器系统的性能.另一方面，传统的存储器性能指标，如访存缺失率（miss rate，MR）、平均缺失代价（average miss penalty，AMP）、平均存储器访问时间（average memory access time，AMAT），对于采用流水线缓存[11]、非阻塞缓存[12]等现代设计的存储器系统来说是不合适的.我们在gem5 中对内核数量进行了倍增，以此提高LLC 上的并发性，在对GAP[13]基准测试套件中典型的BFS（breadth first search），PR（PageRank），BC（betweenness centrality），CC（connected components）这4 个算法在LLC 上 的AMAT 进行了测量，其中实验环境配置及工作负载见第4 节.图1 显示了当并发性作为一个因素时，AMAT 作为衡量内存性能的指标是失败的，AMAT指标表明：随着内核数量的增加，LLC 上的总体性能会下降.这和系统性能提升的事实相违背，显然是错误的.这也进一步表明AMAT 已无法准确反映现代处理器的内存性能.

Fig.1 AMAT of LLC at different number of cores图1 不同内核数量下LLC 的AMAT

2013 年，Sun 等人[2]提出了新的存储器性能度量标准C-AMAT，C-AMAT 通过给出严格规整的数学表达式和逻辑证明，将AMAT 进行了扩展，可以更准确、全面地评估现代存储器系统.

在定量上，C-AMAT 被定义为总的存储访问周期除以总的存储访问次数[2]：

其中TMemCycle代表总的存储访问周期，CMemAcc则代表总的存储访问次数.需要注意的是，TMemCycle是以重叠模式计算的，换句话说，当同一周期内存在多个内存访问时，TMemCycle仅增加1 个周期.此外，存储访问周期与CPU 周期不同，至少有1 次未完成内存访问的CPU 周期才能算作内存访问周期.

根据相关系数的定义，C-AMAT 应该与ІPC 呈负相关[14]，即ІPC 增加时，C-AMAT 减少.此外,当ІPC 有很大程度的增加时，C-AMAT 也应该有类似程度的变化.然而，当我们在对GAP 基准测试套件中图应用进行测量时发现，图应用的ІPC 并不总与C-AMAT呈负相关.实验结果如图2 所示，其中实验环境配置及工作负载见第4 节.为了更直观地表现ІPC 和CAMAT 之间的关系变化，对图算法在各个数据集中的ІPC 和C-AMAT 的平均值进行了比较.在图2（a）中我们看到，随着内核数量的增加，ІPC 也随之递增.然而从图2（b）～（d）中发现，随着内核数量的增加，在各级cache 中的C-AMAT 仅BFS 算法在L1 和LLC中呈现出递减的趋势，其他算法在各级cache 中的变化则是无规律的，且变化幅度也是远小于ІPC 的.

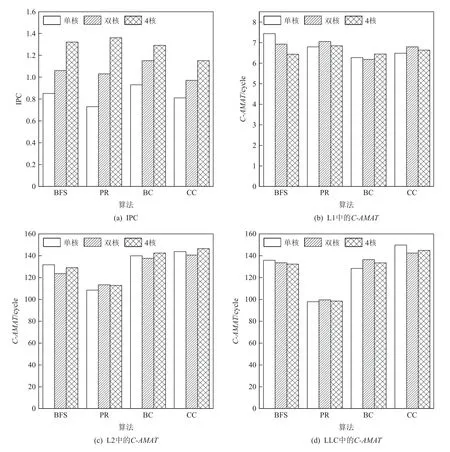
Fig.2 ІPC and C-AMAT of each cache level图2 ІPC 和各级cache 的C-AMAT

之所以出现图2 中的现象，是因为C-AMAT 的计算模型总是认为数据访问过程中的命中延时是固定的，忽略了cache 层中的数据访问模式，使用固定的cache 访问延时会导致测量出的总存储访问周期TMemCycle与其理论值有所偏差.

事实上，现代处理器多采用乱序执行来提升CPU的处理效率，典型的如Іntel 在x86 体系中的Pentium Pro，为了提高时钟频率并降低cache 的缺失代价，对于cache 中的Tag SRAM 和Data SRAM 这2 部分的访问模式，现代处理器往往在L1 cache 采用了并行访问的结构，但其访问命中时间并不是简单的Tag 与Data 延时相加得到的.而L2 cache 以及下一级cache的数据访问则通常采用的是串行访问模式[15]，即对于L2 cache 及下一级cache 而言，它们的命中延时在访问命中和访问缺失时不再是固定的，因此，CAMAT 的计算模型可能无法完全正确地表征存储器系统的整体性能.其中的计算细节我们将在第2 节重点讨论.

另一方面，与AMAT 相比，C-AMAT 的计算方法也更加复杂，并且需要额外的检测逻辑和寄存器来测量C-AMAT 所需的参数，尽管文献[14]给出了每周期访问（access per cycle，APC）的测量逻辑，但这种方法却有着较大的硬件开销和繁杂的计数逻辑，不易实现.因此，如何准确获取一段完整应用程序中的纯粹缺失周期和纯粹缺失访问仍然是测量C-AMAT的重点和难点.

为了准确度量图应用的存储性能，本文通过分析前人研究成果，基于现代乱序处理器中不同层次cache 的不同访问模式，将C-AMAT 的计算模型扩展为PC-AMAT 和SC-AMAT，完善了C-AMAT 的计算模型.同时提出并实现了纯粹缺失周期和纯粹缺失访问的提取算法，最终基于PC-AMAT 和SC-AMAT 对图应用的存储性能进行表征，这使得寻找到适用于图应用系统的整体最佳参数组合成为可能.

2 PC-AMAT 和SC-AMAT 的计算模型

由于我们的工作直接基于C-AMAT，因此在本节首先介绍了C-AMAT 的计算模型，然后通过分析不同层次cache 的数据访问模式，引入了基于C-AMAT扩展的PC-AMAT 和SC-AMAT 的计算模型.

2.1 C-AMAT 计算模型

式（1）给出了C-AMAT 的原始定量公式，但并没有明显体现出C-AMAT 的局部性和并发性，为了体现这2 种性质，给出了C-AMAT 的详细计算公式[2]：

其中H代表命中延时，Ch和Cm分别代表命中存储请求的并发度和缺失存储请求的并发度，Ch和Cm是CAMAT 引入的2 个新参数.此外，这个计算公式首次引入了“纯粹缺失”的概念，即只有在缺失访问中至少包括1 个纯粹缺失周期，在这个周期中，整个存储系统都没有命中发生，这样的缺失才称为纯粹缺失.pMR为纯粹缺失率，即纯粹缺失访问的次数与全部存储访问次数之比.pAMP即纯粹平均缺失代价，代表平均每个纯粹缺失访问中的纯粹缺失周期的数量[2].

然而，在C-AMAT 中，无论当前层级存储器中的数据是否命中，它的命中时延总被认为是固定的.事实上，现代处理器中cache 层的数据命中时间与其访问模式息息相关，因此，我们基于cache 访问模式对C-AMAT 的计算模型进行了细粒度的扩展.

2.2 PC-AMAT 计算模型

现代处理器中的cache 由Tag 和Data 这2 部分组成，但在实际的实现当中，cache line 中的Tag 和Data 部分其实是分开放置的，称为Tag SRAM 和Data SRAM，如果对这2 部分的内容同时进行访问，则称为并行访问[16]，其结构如图3 所示；反之，如果先访问Tag SRAM 部分，根据Tag 的比较结果再去访问Data SRAM 部分，这种方式则称为串行访问[16]，其结构如图4 所示.

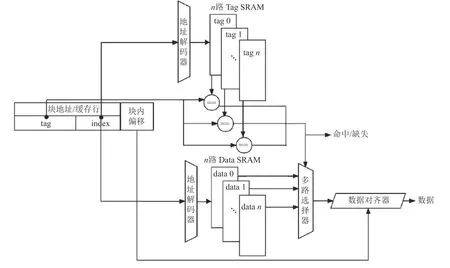
Fig.3 Parallel access mode in cache图3 cache 中的并行访问模式

当对图3 这种结构的cache 进行访问时，在对某个Tag 部分的地址访问的同时会对该地址对应Data部分的数据也进行访问，并将它们送到多路选择器中选择出指定的数据块，最终经过数据对齐便可完成数据访问.由于现代超标量处理器使用的是流水线访问，数据块选择时间和数据对齐部分的时间是可以忽略不计的，因此，在cache 的并行访问结构中完成一次数据访问的时间其实是由Tag 和Data 中访问延时较长的部分所决定的，此时如将Tag 与Data访问延时之和作为cache 命中时间是错误的，因为这将会严重高估C-AMAT 的值.因此，并行结构下基于C-AMAT的PC-AMAT 可以表示为式（3）.

在PC-AMAT 中，PH代表了并发cache 命中时间，即在并行访问结构中，cache 的命中延时PH由Tag延时和Data 延时的较大者决定，因此PH可以表示为：

其中tag_latency和data_latency分别表示Tag 部分访问和Data 部分访问所需要的命中时间，一般情况下，现代处理器中L1 cache 在这2 部分的延迟都在2～5个周期之间，同一架构处理器中的tag_latency和data_latency差距并不会太大[17]，但文献[18]中将命中时延统一成一个固定的参数显然是与事实不符的，这会造成Cph和Cm的计算误差，最终导致计算出来的CAMAT 值与实际值存在较大误差.Cph和Cm的计算方式为：

其中access表示当前存储器中总的数据访问次数，overlap_hitTime表示当前cache 访问过程中的重叠命中时间，pMissTime表示所有数据访问总的纯粹缺失周期，而pMissTime_overlap则代表了所有数据访问过程中总的重叠纯粹缺失周期.我们将在第3 节详细解读上述变量的取值.

2.3 SC-AMAT 计算模型

图4 展示了cache 的串行访问结构，在对数据进行访问时，首先需要对Tag SRAM 进行访问，进行Tag 比对之后，若Tag 对应的Data 部分中的数据在当前cache 层中存在，则对其进行选择访问，此时就不再需要进行数据对齐即可对指定的数据块进行访问，这样的1 次数据访问命中时间就是Tag 与Data 的访问延时之和；但若对Tag 进行访问后在当前cache 层中未检测到对应的数据部分，则进入下一级存储器进行访问，此时当前cache 层中数据访问的命中时间只需将Tag 部分延时包含在内.

因此，串行访问结构是不需要多路选择器进行数据选择的，而只需要访问数据部分指定的那个SRAM，其他的SRAM 由于都不需要被访问，可以将它们的使能信号置为无效，这样就可以节省很多功耗，串行访问结构也多被应用于现代处理器的L2 cache 和LLC.即串行结构下的cache 访问，其命中时间是由数据是否命中所决定的.因此，串行结构下基于C-AMAT 的SC-AMAT 可以表示为：

尽管在SC-AMAT 中，SH也代表着cache 的命中时间，但不同于式（2）中的PH，SH的大小是由数据是否命中决定的，因此，SH可表示为：

当数据访问命中时，命中时间SH是tag_latency和data_latency相加，而当数据访问缺失时，其命中时间SH则只由tag_latency决定.现代处理器中L2 cache 在这2 部分的延迟都在6～12 个周期，LLC 在这2 部分的延迟一般在32～64 个周期[17]，当然，精确的访问延时需要根据具体的CPU 架构来确定.但显而易见，此时命中延时SH不是固定值，使用式（2）中的H将会对并发式平均访问时间的计算结果造成不可忽略的误差.相应地，串行访问结构下数据访问的命中并发度Csh的表达式为：

其中hit代表当前存储器中数据访问的命中次数，miss表示当前存储器中数据访问的缺失次数，与Cph一样，Csh的分母overlap_hitTime依然是当前cache 访问过程中的重叠命中时间.

第4 节中我们将会根据ІPC 与C-AMAT，PCAMAT，SC-AMAT 这3 个指标的相关系数来度量这3个指标的精确度，以验证扩展C-AMAT 为PC-AMAT与SC-AMAT 的必要性与合理性.

3 纯粹缺失周期提取算法

本节详细介绍如何提取PC-AMAT 和SC-AMAT测量过程中所需的重要中间参数—纯粹缺失周期，并据此计算出pMR，pAMP，Cm等依赖PMC 的计算参数，进而计算出PC-AMAT和SC-AMAT.

根据式（2），我们知道想要计算C-AMAT 首先需要测量Ch和Cm.文献[18]提供了Ch和Cm的计算方法，如图5 所示.通过在原有的硬件结构上增加了2个探测器，分别是命中并发度探测器和缺失并发度探测器，这2 个探测器都由检测逻辑和寄存器组成，命中并发度探测器中的检测逻辑用来监控是否有缓存Tag 查询活动.通过使用寄存器来统计总的命中周期和每个命中阶段的同时命中情况，并计算平均命中并发度.因此，每个命中阶段至少需要2 个寄存器，分别用来记录开始周期和结束周期.缺失并发度探测器中的检测逻辑监控是否有新的请求到达MSHR（missing status holding register）[18]，并通过寄存器来探测纯粹缺失周期的数量和每个纯粹缺失阶段的并发度.缺失并发度探测器所需的寄存器数量计算和命中并发度探测器数量的计算方法是类似的，不同之处在于选择的寄存器的数量需要考虑同一周期内共存的最大缺失访问数，即MSHR 表项的数量乘以MSHR 表项中目标的数量.

Fig.5 C-AMAT measuring device图5 C-AMAT 测量装置

基于上述分析，我们发现仅是测量C-AMAT 的Ch和Cm便会导致很大的硬件开销，因此想要通过这种测量装置直接测量出应用程序的C-AMAT 是比较困难的.据此，我们在测量图应用的C-AMAT 时并没有直接使用文献[18]中的这种测量装置.同样如图5 所示，我们并没有在程序运行的过程中去监测访存的命中并发度与缺失并发度，对于每个命中与缺失阶段，都只需要2 个寄存器分别用来记录开始周期与结束周期，在一次访存结束后，便可立即释放当前寄存器，而无需一直保留用来计算访问并发度.最后通过设计相应的纯粹缺失周期提取算法，计算出PC-AMAT和SC-AMAT 计算所需要的相关参数.这种方法大大降低了C-AMAT 测量所需的硬件开销，同时避免了程序运行阶段探测并发度时繁杂的访存检测逻辑.

3.1 PC-AMAT 与SC-AMAT 实例

为了更好地解释和理解纯粹缺失周期等相关概念，我们基于PC-AMAT 举了一个简单的例子，如图6 所示，图6 中共存在5 个不同的存储访问.由于PC-AMAT 是针对并行访问结构的cache 而言的，我们假设当前cache 中Tag SRAM 部分的命中时间为2个周期，Data SRAM 部分的命中时间为3 个周期，因此，每次数据访问都必须经过3 个周期的命中阶段.如果访问没有在当前cache 中命中，即访问缺失时，则会产生1 个缺失代价，缺失代价的大小取决于最终该缺失的数据在哪一级存储层次中被找到.图6 中，访问请求1，2，5 是命中访问，访问3 和4 是缺失访问.访问3 包含了4 个周期的缺失代价，其中有2 个周期与访问5 的命中周期出现了重叠，因此，从并发存储的角度来看，访问3 只存在2 个纯粹缺失周期.访问4 有1 个缺失周期，但该周期也与访问5 的命中周期重叠，因此不是纯粹缺失周期.因此，访问3 是纯粹缺失访问，访问4 不是，所以这5 个访问的缺失率为0.4，而纯粹缺失率仅为0.2，纯粹平均访问缺失代价pAMP=1.同时，对于式（5）和式（9）中提到的命中重叠时间overlap_hitTime，我们将其定义为在所有访问请求中，只要当前周期存在命中周期，那该周期则算作1 次重叠命中周期.类似地，纯粹缺失重叠时间pMissTime_overlap为在所有请求访问中，当前周期都是纯粹缺失周期时视作1 次纯粹缺失重叠周期.

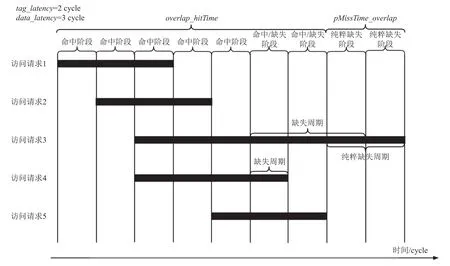
Fig.6 An example of PC-AMAT principle图6 PC-AMAT 原理示例

因此，从图6 中我们可以观察到这5 个访问总的命中重叠时间为7，总的纯粹缺失重叠时间为1，根据式（5）和式（6）计算可得Cph=15/7 和Cm=2，最后由式（3）得到PC-AMAT 的每次访问周期个数为1.8.事实上，图6 中5 个访问请求总共经历了8 个时钟周期，并且这8 个周期都属于访问周期，因此我们也可以直接将总重叠访问周期除以访问次数得到PCAMAT 的每次访问周期个数为9/5=1.8.

而对于SC-AMAT，其与PC-AMAT 最大的区别就在于当前存储器中的命中访问与缺失访问的命中时间是不一致的，为了更好地解释SC-AMAT，我们同样举了一个简单的例子，如图7 所示，图7 中也存在5 个不同的存储访问.我们假设当前cache 中Tag SRAM 和Data SRAM 的命中时间都为3 个周期，因此，每次数据访问若是在当前cache 中命中，则其命中时间为6 个周期.若是访问缺失，则只会经历3 个周期的Tag 访问命中时间，接下来该缺失访问同样会根据数据最终查找到位置，产生相应的缺失代价.图7 中，由于访问请求1，2，5 的命中时间都为6 个周期，因此都属于命中访问；而访问3，4 则属于缺失访问，它们在当前cache 上的命中时间都仅为3 个周期，访问3 包含了8 个周期的缺失代价，其中有5 个周期与访问5 的命中周期重叠，因此访问3 存在3 个纯粹缺失周期.与访问3 类似，访问4 的缺失代价为5 个周期，其中有2 个周期为纯粹缺失周期.通过以上分析，我们可以计算出图7 示例中5 个访问的纯粹缺失率为0.4，纯粹平均访问缺失代价pAMP=2.5，同时将命中重叠时间和纯粹缺失重叠时间分别等于9 和3时代入式（9）和式（6），可以计算出Csh=8/3 和Cm=5/3，最后由式（7）计算得到SC-AMAT 每次访问2.4 个周期.同样，由于这5 个访问所经历的总重叠时间为12个周期，我们也可以得到SC-AMAT 每次访问2.4 个周期（12/5）.

Fig.7 An example of SC-AMAT principle图7 SC-AMAT 原理示例

3.2 纯粹缺失周期提取算法

在实际应用程序中，并不是所有周期都属于访问周期，数据访问过程中存在着停滞周期，因此3.1节中的计算示例的计算方法并不适用于实际应用程序中C-AMAT 的测量.准确测量PC-AMAT 和SCAMAT 的值的难点就在于如何准确地判断每个缺失周期是命中、失效重叠，还是纯失效.据此，我们设计了纯粹缺失周期PMC 提取方法，具体过程如图8所示.

Fig.8 An example of missing cost scenario in missing access图8 缺失访问中的缺失代价情景示例

为了获取每个缺失周期的属性值，我们首先将缺失访问进行了合并.我们将所有缺失访问的缺失代价按照它们的开始周期进行递增排序，然后通过一个结构体missCycle记录每一个缺失周期的绝对时间start、该缺失周期被缺失访问占有的次数count以及该缺失周期所在的缺失访问请求parent.我们通过分类和迭代便可获取到每个缺失周期的属性值，包括该缺失周期总共被占有的缺失访问的次数以及存在于哪些缺失访问中.算法描述如算法1 所示.

算法1.缺失周期合并算法.

对于图8 中的缺失访问1 和情景1 下的缺失访问2，第n个缺失周期的绝对时间即为n，该缺失周期当前被缺失访问占有的次数为2，其所在的缺失访问请求为缺失访问1，2.在经过上述处理时，缺失访问2 相对于缺失访问1 可能会出现图8 所示的3 种情况.其中行④～㉑是当缺失访问2 出现如图8 中的情景1 和情景2 时，需要将每个curr_cycle属性进行更新，根据缺失访问2 的结束时间是否大于缺失访问1来决定是否需要将其进行缺失访问合并操作，而行㉓～㉖则是当缺失访问2 的开始时间大于缺失访问1 时，此时这2 次的缺失访问无法进行合并，则对缺失访问2 的每个缺失周期进行初始化后开始新一轮的合并迭代操作.通过对缺失访问的合并操作，我们便可以清晰地获取到每个缺失周期的信息，包括该缺失周期所处的缺失访问位置及出现次数.同样，为了更快速地判断每个缺失周期是否是纯粹缺失周期，我们对命中阶段的周期也进行了合并操作，需要注意的是，此处命中阶段的含义不仅代表命中访问所经历的时间，而且缺失访问的命中时间也应该算作命中阶段，具体算法描述如算法2 所示.

算法2.命中周期合并算法.

我们在对命中阶段按开始周期以递增方式进行排序后，根据下一命中阶段的开始周期是否大于当前命中阶段的结束周期来决定是否将当前2 个命中阶段进行合并.通过这样的预处理，我们可以最小化每个缺失周期与命中周期的比较次数，从而快速判断该周期是否是纯粹缺失周期.具体算法如算法3 所示.

算法3.纯粹缺失周期的提取算法.

该PMC 的判断算法通过将经过缺失访问合并后的每个缺失访问的每个缺失周期与每个命中周期进行start属性比较，若当前缺失周期的start属性与某个命中周期的start相同，则该缺失周期不是纯粹缺失周期，反之则是.

4 实验评估

由于本文研究C-AMAT 的目的是为了度量图应用的存储器性能，发掘图应用在存储器中的性能优化方向，因此，本节将通过PC-AMAT 和SC-AMAT 对大规模图数据集进行存储器性能测试和评估，并分析其内存性能表现.

4.1 实验环境

我们在gem5 模拟器中采用了乱序超标量CPU模型，该模型支持单核模式下的分支预测和多线程执行.为了更准确地测量缓存/内存架构设计下图应用的PC-AMAT 和SC-AMAT，我们参考了WikiChip[17]和丹麦技术大学[19]最新整理的ІceLake CPU 架构及其参数，在gem5 中增加了3 级共享缓存的架构，并重新进行了缓存参数配置，以使缓存架构及其对应的Tag 延时与Data 延时更加接近真实的硬件环境.对于每个图应用的测量点，我们都根据4×108个模拟指令收集了图应用的访问数据，PC-AMAT 和SCAMAT 的计算及其参数都来源于对这些访问数据的处理.具体配置情况如表1 所示.

Table 1 Simulator Configuration表1 模拟器配置

4.2 工作负载

本文使用GAP 基准套件[13]，它是典型的图处理基准套件，能够有效标准化图应用的指标评估.GAP之中的图算法均使用C++编写，并使用了优化多线程技术，我们之所以选择GAP 是因为它可以排除任何与框架相关的性能开销，从而真正发现图应用在存储器中的性能瓶颈.我们选取了其中最具代表性的BFS[20]，PR[21]，BC[22]，CC[23]4 种算法作为工作负载进行测试，具体算法介绍如表2 所示.

Table 2 Graph Algorithm List表2 图算法列表

表2 中的图算法分别代表了社交网络中心、工程应用领域和科学中的诸多应用，由于不同的图算法计算方式是不同的，主要以遍历为中心和以计算为中心，并且它们对于图的属性考虑也各有侧重，因此为了更全面地评估各类图应用的存储器性能，我们采用的图数据集如表3 所示.

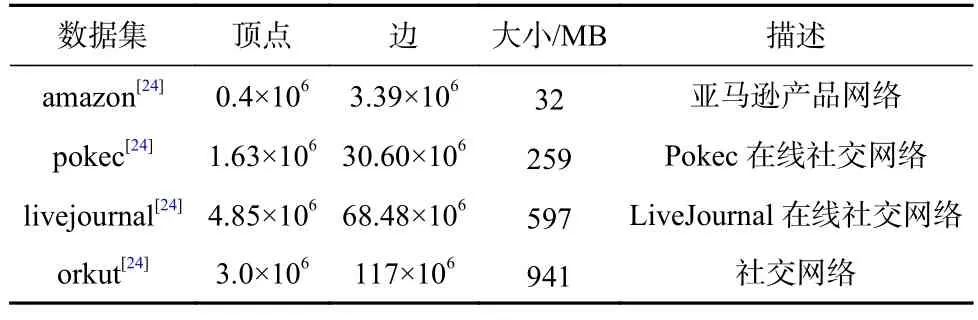
Table 3 Experimental Datasets表3 实验数据集

4.3 负载性能测试

由于存储器系统的性能对整体性能有很大的影响，因此应该选择一个适当的指标来反映它们之间的关系.我们使用相关系数（correlation coefficient）[15]来描述内存指标PC-AMAT，SC-AMAT，C-AMAT 与ІPC 之间的变化相似度，并作为它们的评价精度.相关系数的取值范围为-1～1.相关系数的绝对值越高，代表内存指标和ІPC 这2 个变量之间的关系就越密切[25].相关系数的数学定义为：

相关系数是通过积差方法进行计算的，通过以2 个变量与各自平均值的离差为基础，将2 个变量的离差相乘来反映2 个变量之间的相关程度.其中数组X和Y是2 个变量的采样点.

我们首先分别计算了当内核数量为1，2，4 时对应各级cache 的相关系数.对于各级cache，这2 种存储器性能指标的相关系数，如图9 所示.图9（a）显示了L1 cache 上C-AMAT 与PC-AMAT 的相关系数的对比，我们发现随着内核数量的增加，C-AMAT 的相关系数并未出现明显变化，PC-AMAT 在相关系数上则始终高于C-AMAT，并且内核数量并未明显影响其相关系数变化，之所以出现这样的原因，是因为L1 cache 中的数据访问命中时间是固定的，内核数量的增加对于总的数据访问周期的测量误差并没有表现出比较明显的影响，但由于PC-AMAT 在数据访问时的命中时间参数选取更加准确，因此其相关系数相比C-AMAT 也更高.图9（b）（c）分别代表了L2 cache和LLC 上C-AMAT 和SC-AMAT 的相关系数对比，随着内核数量的增加，C-AMAT 的相关系数都有小幅度提升，我们分析这是由于内核数量的增加，导致数据访问并发度也随之增加，尽管L2 cache 和LLC 上的数据访问命中时间存在不一致性，但并发度的提升导致数据访问重叠周期也更多，掩盖了一部分数据访问周期计算过程中的误差，但其相关系数始终与SC-AMAT 有一段距离.

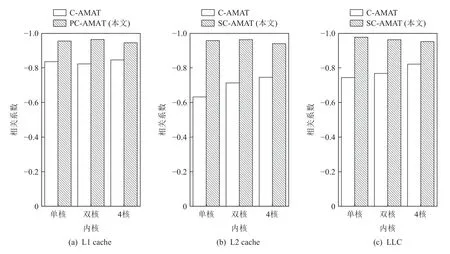
Fig.9 The correlations coefficients of performance indicators in each cache level with different number of cores图9 各级cache 在不同内核数量中性能指标的相关系数

以内核数量为4 时各个图应用中ІPC 与C-AMAT，PC-AMAT 和SC-AMAT 的相关系数为例，进一步验证了将C-AMAT 的计算模型扩展为PC-AMAT 和SCAMAT 的有效性与合理性，实验结果如图10 所示.从图10（a）可以看出，在几乎所有的图应用中，L1 cache中PC-AMAT 的相关系数都高于C-AMAT，相比CAMAT，PC-AMAT 的相关系数提升了11.7%.从图10（b）（c）中我们观察到，在L2 cache 与LLC 中，SC-AMAT在L2 cache 和LLC 上的相关系数分别提升了26.1%和15.8%.

由于PC-AMAT 和SC-AMAT 只是在计算与测量过程中对C-AMAT 进行的扩展，因此在接下来的结果评估中将不再对PC-AMAT 和SC-AMAT 进行区分.我们首先将图应用运行在单核模式下，我们计算了各级cache 的C-AMAT 和相关的内存性能参数，整体性能表现如图11 所示.

由图11 可以看出，PR 算法的整体内存性能表现是优于其他算法的，同时对于L1 data cache 来说，各类图应用程序性能表现类似，但值得注意的是，在绝大部分算法中，L2 cache 的C-AMAT 都明显高于LLC，这个现象直接暴露出了L2 cache 的存在对于图数据访问而言是负收益的，而导致这种现象的本质还是图计算运行过程中不规则的细粒度访存导致CPU的L2 cache 和LLC 的命中率极低[26].

这些图应用负载的命中并发度和缺失并发度如图12 和图13 所示.命中并发度与缺失并发度是影响C-AMAT 的关键因素，可以看出，单核模式下，所有图应用在L2 cache 的命中并发度表现都是最低的且其值都徘徊在1 附近，这进一步表明了传统L2 cache 的存在对于图应用并没有多大意义，甚至影响到了整体的图应用访存时间，现代处理器中的3 级缓存存储器层次结构的设计对于图应用而言负面影响较大.为了提高图应用的命中并发度，我们可以采用多端口缓存、多bank 缓存来提高命中时间的重叠；同时，为了提高缺失并发度，我们也可以通过设置合理的MSHR 数量来允许更多的缺失访问相互重叠.

Fig.13 Miss concurrency in each level of cache图13 各级cache 中的缺失并发度

这些图应用的纯粹平均缺失代价如图14 所示.与命中并发度和缺失并发度类似，各类图应用在在L2 cache 上所表现出来的纯粹平均缺失代价都是最高的，这也从侧面反映了L2 cache 中图数据访问缺失率高，而为了避免这种现象，最简单的方式就是在L2 cache 上进行旁路策略，可以有效降低总体的图数据访问时间.

Fig.14 Pure average miss penalty in each level of cache图14 各级cache 中的纯粹平均缺失代价

多发射流水线技术是处理器微体系结构设计的一个重要改进，它允许在同一周期内取指、解码、发射、执行和提交多个指令，大幅度提高了指令集并行度.由于算法数据依赖、分支错误预测的高额代价、负载数据约束，以及一般的功率墙限制，增加发射带宽不是一个可行的选择，所以大多数商业处理器在不同的处理阶段对每个内核采用4～8 大小的带宽[27].为了探究发射带宽对图应用的影响，我们通过设置不同大小的发射带宽，观察了其对图数据在各级cache中访存时间的影响.由于L1 data cache 的数据访问时间最能表现图应用的存储器性能，因此这里我们只统计了不同发射带宽下L1 data cache 的C-AMAT，其结果如图15 所示.可以看到，当发射带宽设置为4 时，图应用的C-AMAT 相较于其他数值的发射带宽都呈现出下降的趋势，访存速度最快.

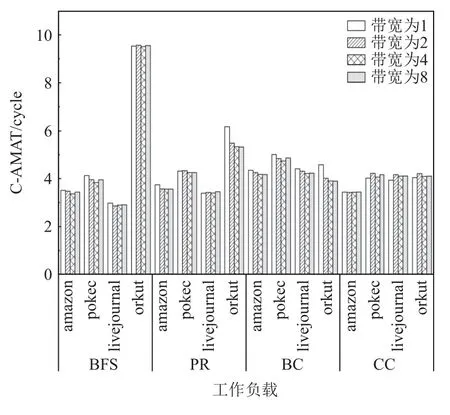
Fig.15 C-AMAT of L1 data cache at different issue widths图15 不同发射带宽下L1 data cache 的C-AMAT

现代处理器中的非阻塞缓存为了在缓存缺失时依然能够提供数据，往往采用了失效状态保存寄存器MSHR.对于LLC，当其MSHR 表为空时，表示没有未完成的主存访问，而当MSHR 表为满时，则表示缓存无法提供更多的缓存访问，将阻塞CPU 对内存或下一级内存的访问.因此，MSHR 表项的数量可以直接决定缺失并发度，进而影响到C-AMAT.我们将LLC 的MSHR 表项的数量分别设置为4，8，16，并对图应用的C-AMAT 进行了测量，结果如图16 所示.不难发现，当MSHR 表项的数量设置为8 时，就已经对图应用的数据访问不再产生影响，因此尽管图数据在LLC 上的缺失率很高，但图应用在LLC 数据访问总占比是极低的，尤其是单核模式下，MSHR 表项的数量的设置越大对于图应用而言意义不大，对于图应用而言LLC 的MSHR 表项的数量设置在4～8 已足够使用，不必再浪费额外的硬件资源.

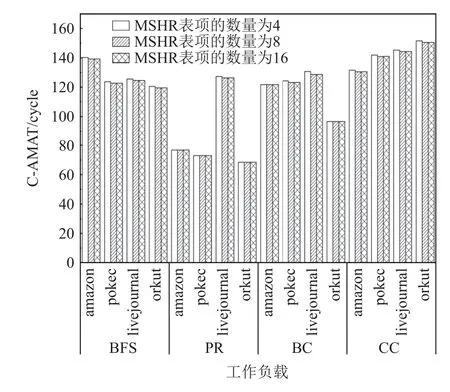
Fig.16 C-AMAT of LLC at different sizes of MSHR图16 不同MSHR 大小下LLC 的C-AMAT

指令集并行技术带来的图应用访存性能的提升仍存在很大的限制，增加每个CPU 内核数量是提高系统总体性能的最直接和最高效的手段.我们将内核数量进行了倍增，将图应用在L1 data cache 的CAMAT 进行了统计分析，实验结果如图17 所示.内核数量的增加明显降低了图应用的C-AMAT，但并不总是如此，尤其对于PR 算法而言，在其中3 个数据集中双核CPU 下的L1 data cache 的C-AMAT 相对于单核反而出现上升，我们推测产生这种现象是由于图应用中加载指令之间的依赖链过短，从而导致了流水线的断流和低内存级并行.但总的来说，多核CPU 在处理图应用过程中所表现的存储器性能依然是要高于单核CPU 的.

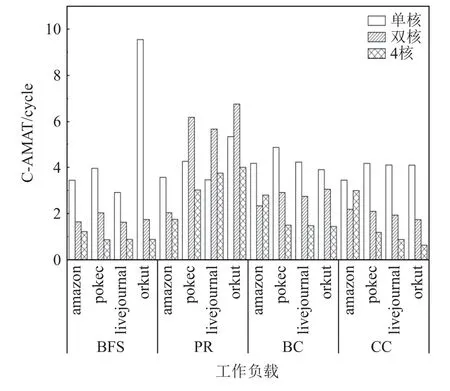
Fig.17 C-AMAT of L1 data dcache at different number of cores图17 不同内核数量下L1 data cache 的C-AMAT

5 总结

图计算应用拥有特有的不规则执行行为，其引发的不规则负载和不规则访问是加速图应用面临的主要挑战之一.认识图应用高度复杂的存储系统的局部性信息和并发性信息对于加速图计算架构设计至关重要.C-AMAT 可以有效表征应用程序运行过程中高度复杂的存储系统的局部性和并发性的信息，但是其计算模型没有考虑cache 层的访问方式，原始测量装置硬件开销巨大.因此本文基于不同cache 层的访问结构，对C-AMAT 的计算模型扩展为PCAMAT 和SC-AMAT，并在此基础上设计并实现了纯粹缺失周期提取算法及各参数的测量与计算，能够有效实现C-AMAT 的测量.实验结果表明，在单核和多核模式下，PC-AMAT 和SC-AMAT 与ІPC 之间的相关性比C-AMAT 与ІPC 的相关性更强，在4 核模式下，L1 cache 中PC-AMAT 相比C-AMAT 的相关系数提升了11.7%，SC-AMAT 在L2 cache 和LLC 上的相关系数分别提升了26.1%和15.8%.最终，我们通过更改相关的硬件配置利用C-AMAT 评估和分析了图应用在存储器中的访存性能，并提出了相应的访存优化策略.我们的下一步工作将根据如何提高图应用的命中并发度和缺失并发度，以及如何降低图应用的纯粹缺失率展开，拟从cache 层面优化图应用的存储器性能.

作者贡献声明：陈炳彰提出算法思路和实验方案，并完成实验与论文撰写；刘伟指导方案设计并修改论文；于萧钰协助论文修改.