基于输入整形的丝杠传动的振动误差补偿*

郑飂默,栾昊轩,李备备

(1.中国科学院沈阳计算技术研究所,沈阳 110168;2.沈阳中科数控技术股份有限公司自动化装备事业部,沈阳 110168;3.中国科学院大学,北京 100049)

0 引言

制造业是一个国家的兴国之器和强国之基,为我国经济的快速发展注入了强大动力。近年来,我国对高端数控机床的性能要求进一步提高。随着现代制造要求高速化和高精度,丝杠传动系统的动态特性建模及其仿真愈发重要[1]。研究传动系统的动态特性能够帮助机床伺服反馈系统的设计,极大地提高机床响应特性和精度。滚珠丝杠进给系统主要包含伺服电机、联轴器、底座、滚珠丝杠、导轨、工作台等。在高速度和高加速度下,电机的驱动力增加,导致滚珠丝杠传动部件之间的作用力增加,造成一些部件的弹性变形和振动[2],因此滚珠丝杠传动系统的误差补偿以及工件的加工稳定性成为了研究热点与突破点。

刘吉柱等[3]所设计的微动补偿平台具有良好的动态特性,定位系统具有良好的误差实时补偿效果,针对X、Y方向的振动范围由补偿前的3.5 μm,补偿后减小到1 μm的范围内,有效的提高了系统的定位精度。宣贺等[4]使用ADAMS软件对滚珠丝杠传动系统进行振动仿真分析,得到了卧式和立式的频响曲线,并结合HyperMesh软件建立了卧式和立式滚珠丝杠进给机床的多柔体模型;曾浩然等[5]对滚珠丝杠传动系统轴向的非线性振动进行分析,发现丝杠传动系统中轴向振动同时出现混沌运动和周期运动,并且当激励频率和阻尼系数增大时,系统周期性增强;WU等[6]针对滚珠丝杠进给系统的振动特性,提出一种混合建模方法来研究其动力学行为;GAO等[7]进行了滚珠丝杠进给系统的横向振动的动力学建模与分析研究,使用了PSO算法进行动态参数辨识;LI等[8]针对基于柔性动力学模型的滚珠丝杠传动系统进行了单轴的振动抑制研究,在丝杠传动系统中引入了输入整形器,并最终使用ZVD输入整形器进行振动误差补偿。

本文以X-Y轴滚珠丝杠运动平台为研究对象,首先通过拉格朗日方程建立X、Y方向的振动动力学模型[9-10],建立数学模型并分析传递函数进行降阶,计算ZV输入整形与ZVD输入整形的参数,并在Simulink中仿真实验,比较得出最优方案,最后在实验平台进行验证,并分析两种整形器补偿效果不同的产生原因。

1 滚珠丝杠传动系统的动力学建模

1.1 振动误差来源分析

如图1所示,电机运转时丝杠受力不均匀,发生弹性形变,因此运动平台在运动中会产生振动误差[11-12],此外,运动平台轴向的推力不稳定也会导致波动,引起轴承副的配合部位发生弹性形变,是导致振动误差的主要原因,从而影响平台的定位精度。

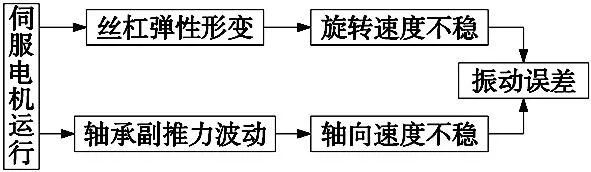
图1 振动误差来源分析

1.2 X、Y方向振动动力学建模

如图2a所示是本实验所用滚珠丝杠传动实验平台,图2b是根据实验平台建立的三维模型。

(a) 实验平台 (b) 三维模型

为建立两个方向上的动力学模型,本文通过改进集中参数法与分布式参数法相结合的方法[7]建立拉格朗日方程。首先建立进给系统的混合模型,工作台相当于集中质量单元,简化后的滚珠丝杠传动系统动力学简图如图3所示,丝杠相当于3个等集中质量和惯性矩,每一段都由弹簧阻尼单元连接,螺母、轴承分别相当于弹簧阻尼单元。此模型考虑影响工作台进给方向的运动。

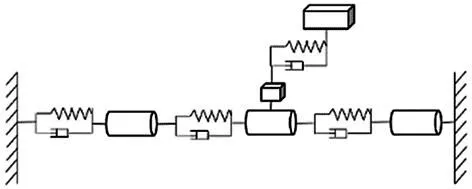
图3 系统结构简图

其中共有5个自由度,分别为:θ1为左段丝杠转动角;θ2为中段丝杠转动角;θ3为右段丝杠转动角;x1为螺母副位移距离;x2为运动平台位移距离。

1.2.1 系统的总动能

由于丝杠被分为了3个部分,因此需要分别计算左段丝杠的动能、中段丝杠的动能以及右段丝杠的动能,相加即可得到丝杠的总动能,再根据丝杠总动能、工作台的动能以及螺母的动能,确定系统总动能。

(1)

表1 动能方程参数物理意义及取值

1.2.2 系统的总势能

由于丝杠被分为了3部分,分别计算左段丝杠的势能、右段丝杠的势能、丝杠螺母的势能,相加即可得到丝杠的总势能,确定系统总势能。

(2)

表2 势能方程参数物理意义及取值

1.2.3 系统的总耗散能

由于丝杠被分为了3部分,故而分别计算左段丝杠的耗散能、右段丝杠的耗散能、中段丝杠的耗散能,相加即可得到丝杠的总耗散能,再根据丝杠总耗散能、螺母的耗散能、运动平台的耗散能,确定系统总耗散能。

(3)

表3 耗散能方程参数物理意义及取值

1.2.4 进给系统的微分方程

根据拉格朗日方程,系统的总动能、总势能、总耗散能之间的关系为:

(4)

将总动能、总势能、总耗散能带入方程可得系统振动微分方程组:

(5)

通过拉氏变换求解微分方程组:

(6)

求得开环传递函数为:

(7)

带入物理参数可得X轴开环传递函数与闭环传递函数,闭环传递函数降阶后可得:

(8)

同理可得Y轴闭环降阶传递函数为:

(9)

2 输入整形器的Simulink仿真实验

整形器里面含有一系列的不同幅值和时滞的脉冲[13-14]。而其中的关键就是计算出每一个脉冲信号的幅值以及它们各自的时滞[15]。而常见的输入整形器主要有ZV输入整形器和ZVD输入整形器。

2.1 X轴输入整形

ZV输入整形:

(10)

ZVD输入整形:

(11)

将结果在simulink中进行仿真实验,结果如图4所示。

图4 X轴输入整形仿真

2.2 Y轴的输入整形器

ZV输入整形:

(12)

ZVD输入整形:

(13)

仿真实验结果如图5所示。

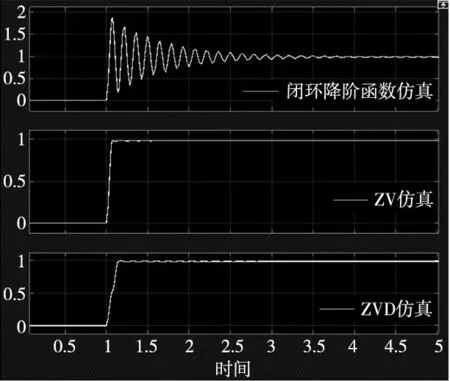
图5 Y轴输入整形仿真

3 输入整形的实验验证

如图6所示是本文使用的X-Y轴丝杠传动实验平台,该实验平台的控制模块是基于自主研发的运动控制器整合的输入整形算法模块。

图6 X-Y轴丝杠传动实验平台

将传递函数的频率以及阻尼系数输入算法模块中进行实验,在进行X、Y两个方向运动时,稳定性与调整速度都有明显增强。

如图7所示,在X轴方向,ZV输入整形器与ZVD输入整形器的振动误差补偿效果相近,而使用ZV整形器进行补偿的方案调整时间更短。因此在X轴方向上采用ZV输入整形器进行补偿。

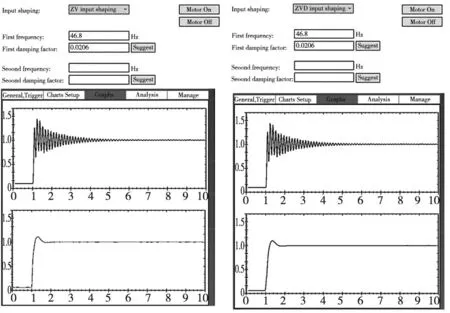
(a) ZV输入整形 (b) ZVD输入整形

如图8所示,在Y轴方向,ZV输入整形器与ZVD输入整形器区别较大,使用ZV输入整形器后,运动平台的稳定性远不及ZVD输入整形器的补偿效果。因此,在Y轴方向上采用ZVD输入整形器进行补偿。

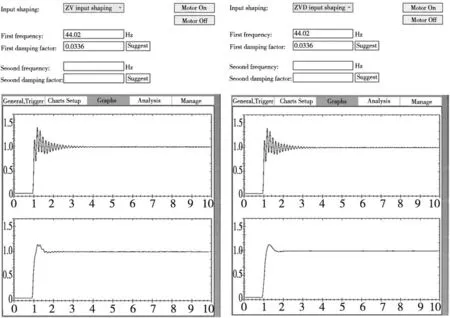
(a) ZV输入整形 (b) ZVD输入整形

X、Y轴运动平台区别在于负载的大小不同,X轴方向上的负载主要是运动平台,而Y轴方向上增加了X轴的机械结构,整体负载更大,就导致其振动频率更低,更接近整体机床的固有频率。而输入整形器的参数计算都是根据降阶处理过的传递函数,振动频率接近固有频率就会使得传递函数的降阶处理过后的参数不准确,从而引起误差。

4 结论

本文首先通过混合建模法建立了滚珠丝杠传动系统的动力学模型,然后在Simulink中进行不同输入整形器的仿真实验,最后在整合了输入整形模块的自主研发的运动控制器实验平台上进行验证。ZV输入整形器在实验中会带来更短的调整时间,并且在X轴方向上效果略优于ZVD输入整形器。而在Y轴方向上ZVD输入整形器的补偿效果要明显优于ZV输入整形器,这是因为Y轴的运动平台质量更大,因此其振动固有频率比较低,在降阶运算时会带来更多误差,从而导致模型不准确,也就使得ZV输入整形器的补偿稳定性下降。因此,不通过降阶处理就能计算输入整形器参数或是将降阶的过程更精确化就是未来工作的研究重点。