Joint Task Allocation and Resource Optimization for Blockchain Enabled Collaborative Edge Computing

Xu Wenjing ,Wang Wei,* ,Li Zuguang ,Wu Qihui ,Wang Xianbin

1 College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

2 Key Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space,Ministry of Industry and Information Technology,Nanjing 211106,China

3 Department of Electrical and Computer Engineering,Western University,Canada

Abstract: Collaborative edge computing is a promising direction to handle the computation intensive tasks in B5G wireless networks.However,edge computing servers (ECSs) from different operators may not trust each other,and thus the incentives for collaboration cannot be guaranteed.In this paper,we propose a consortium blockchain enabled collaborative edge computing framework,where users can offload computing tasks to ECSs from different operators.To minimize the total delay of users,we formulate a joint task offloading and resource optimization problem,under the constraint of the computing capability of each ECS.We apply the Tammer decomposition method and heuristic optimization algorithms to obtain the optimal solution.Finally,we propose a reputation based node selection approach to facilitate the consensus process,and also consider a completion time based primary node selection to avoid monopolization of certain edge node and enhance the security of the blockchain.Simulation results validate the effectiveness of the proposed algorithm,and the total delay can be reduced by up to 40%compared with the non-cooperative case.

Keywords: blockchain;collaborative edge computing;resource optimization;task allocation

I.INTRODUCTION

With the emergence of computational intensive and delay sensitive applications,such as autonomous driving,augmented/virtual reality (XR),effective utilization of distributed computing resources become more and more important in 5G and beyond networks.Edge computing provides a promising solution to reduce the computing delay in an effciient manner by shifting computing tasks from remote cloud center to the network edge[1,2].However,due to its limited communication,computing,and caching capability,a single ECS often has diffciulty to deal with computing sensitive tasks,especially when massive users have to be supported in hot spot areas [3].In addition,users generally subscribe services from a specifci operator and thus they can only offload computing tasks to their subscribed servers,causing long queuing delay in rush hours.

Collaborative edge computing has been a promising solution by clustering the computing power of nearby ECSs to break the limitation of a single server [4-7].However,due to the competition among operators,ECSs belonging to different operators do not trust each other,resulting in unguaranteed quality-ofservice(QoS)for users and unguaranteed revenues for service providers.In light of this,we propose a collaborative edge computing framework based on consortium blockchain.With the distributed and tamper proof characteristics of blockchain,multi-ECS can build a secure and trusted collaboration platform to provide computing services.The task request,offloading strategies,resource allocation,and computing results will be recorded on the blockchain permanently,which not only ensures the trust and revenues between servers,but also guarantees the QoS of each task.In this paper,we optimize the task offloading strategy and computing resource allocation to minimize the total delay,under the constraint of each edge server.The main contributions can be summarized as follows:

• We propose a consortium blockchain based collaborative edge computing framework,where each ECS belonging to different operators not only maintains the blockchain system but also provides computing services for offloaded tasks.The service requests,task offloading and computing resource optimization,and computing results are recorded on the blockchain in a tampproof manner,and thus the revenues of both service provider and requestors can be guaranteed,and the computing effciiency can be improved.

• We formulate the total delay minimization problem by jointly optimizing task offloading and resource allocation,which is a mixed integer nonlinear programming problem.We apply the Tammer decomposition method and heuristic optimization algorithms to obtain the locally optimal solution,which is guaranteed to converge.

• To facilitate the consensus of the consortium blockchain,we propose a reputation based consensus nodes selection scheme,where only ECSs with high reputation will be chosen for consensus.Thus,the communication overhead during the consensus will be reduced signifciantly.Moreover,to avoid monopolization of certain MEC node,we present a completion time based primary node selection approach,wherein the node providing the least delay for the assigned task will be chosen as the primary node in the next round of consensus.

The remainder of this paper is organized as follows.We discuss related works in Section II and present the system model in Section III.The joint task offloading and resource allocation algorithm is formulated in Section IV.In Section V,simulation results and discussions are presented.Finally,conclusions are given in Section VI.

II.RELATED WORKS

We briefly summarize related works on collaborative edge computing and present the difference with our work in this section.

A cloud-edge unifeid offloading model is proposed in[8],where the offloading for IoT scenario is divided into three layers,including the IoT device layer,edge computing layer,and cloud computing layer,where tasks can be transferred between devices,devices and servers,and between different servers.A distributed computing offloading algorithm is designed in [9]based on game theory,quantifying the calculation delay index and realizing lower time cost.In [10],authors consider a real-time,context-aware collaboration framework,which can achieve collaborative caching and processing,multi-layer interference cancellation,and mobile edge orchestration.

Note that most of the above articles consider a single ECS case,which may not suitable for real applications in practice.In case of multiple servers,some authors also analyze the cooperation between edge and cloud servers.Some efforts jointly consider minimizing system cost or maximizing total utility,and making offloading strategies under resource and delay constraints [4,11-16].In [4],a collaborative vehicular edge computing framework is proposed,considering the collaboration among edge computing anchors,which support both horizontal and vertical collaborations.Then authors in [13] investigate the collaboration between cloud and edge computing.They formulate a joint resource allocation problem to minimize the weighted-sum latency and obtain the closed-form of optimal task splitting strategy by transferring the original joint problem into an equivalent convex optimization problem.Considering the complex resource allocation problem for collaborative MEC,authors in[17] study the user allocation problem under queuing scenario,and propose an algorithm to help reaching the balance between users’benefti and processing delay of the task.Since the arrival and departure of users are unpredictable,the optimization problem is transformed into a boundary problem before processing.To further reduce the completion time,network flow scheduling has also been considered in collaborative computing.In [18],the authors study a data-aware task allocation problem to jointly schedule task and network flows in collaborative edge computing using a multi-stage greedy adjustment algorithm.

However,most of these work ignore the security issue in collaborative ECSs.Although authors in [19]ensure security of transmitted data through encryption and decryption,it may not prevent malicious ECSs giving incorrect results.Some articles rely on the central authentication authority to guarantee security[20-22] and manage user access and data usage.Nevertheless,those centralized mechanisms are vulnerable to single-point failure and can not fti the distributed MEC network.A trust-level based mechanism is proposed in [23],but it is still diffciult to achieve a high trust level in practice.

As a promising distributed technology,blockchain emerges as a promising way to establish cooperative trust among ECSs [24,6,25-27].Authors in [24]devise a blockchain-native edge collaboration architecture and design a two-layer effciient permissioned consensus protocol dedicated to the collaborative task distribution.In[6],authors propose a novel decentralized system which tackles the trust challenge to enable collaborative edge storage based on blockchain.Similarly,a novel blockchain-based decentralized platform is proposed in[25]which employs an incentive mechanism and a reputation system to address the incentive and trust issue respectively.In[26],authors propose a cooperative computation offloading framework for blockchain-enabled MEC systems to enable the joint analysis of the MEC computation rate and the blockchain transaction throughput.However,above articles on MEC frameworks mostly consider from the mobile end-user point of view.Authors in [27] consider the possibility of offloading among edge servers and devise a system model for the Hyperledger Fabricbased task offloading collaboration scheme.

[26-30].In[26],authors jointly optimize the power allocation of the MEC system and the transaction throughput (block size and block generation interval) of the blockchain system.In [27],a permission blockchain is introduced to ensure the security and privacy of users in the process of offloading tasks.

III.SYSTEM MODEL AND PROBLEM FORMULATION

In this section,we present the system model,including the workflow of the computation offloading and the collaborative computing model,and then formulate the joint offloading and task allocation problem.We consider a quasi-static scenario,where the transmit power of users and the distance between user and ECS remain unchanged at each epoch[31].

3.1 System Model

As shown in Figure 1,we consider a typical edge computing scenario,where each BS is equipped with an ECS,which can execute computation tasks for the nearby resource-constrained vehicles or mobile terminals.The computation offloading is executed in a slot-by-slot manner,where at the beginning of each slot,users with computation-intensive and delaysensitive tasks request the computing resources from nearby ECSs.We denote the set of users asU={1,···,i,···,K},whereKis the total number of users during a certain slot.Without loss of generality,we also assume there areNECSs available for computing services,and the set of ECSs is denoted asS={1,···,j,···,N}.In the following,we useUiandSjdenote theith user andjth ECS.

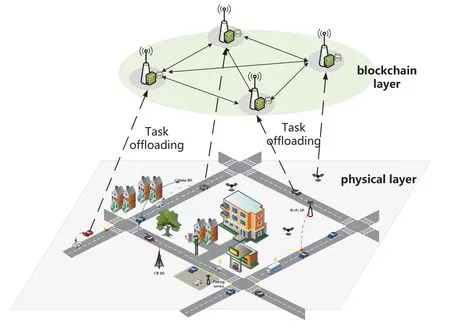
Figure 1.System model.

3.1.1 Computation Offloading Model

Assume that each user can only offload the task to one ECS,and each ECS can serve multiple tasks simultaneously.We introduce a binary variablexij={0,1}to denote the task association,andxij=1 presentsUioffloads task to serverSj,otherwisexij=0.

Considering the wireless transmission between users and ECSs,we assume identical and orthogonal bandwidth resourcesBare allocated to each ECS to avoid mutual interference.Each ECS uses time division multiple access (TDMA) to serve its own users.Denote the set of users served bySjasUjwith a cardinality ofNj.

Moreover,both users and BSs are equipped with a single antenna,then the channel state information(CSI)betweenUiandSjis expressed as:

whereRijis the corresponding distance,α ＞2 is the fading factor andh˜ijis small-scale fading,which obeys a Rayleigh distribution.Then,the information transmission rate can be written as:

whereσ2is the noise power,Piis the transmission power ofui.Then the uplink transmission delay can be calculated as:

whereDiis the data size of the computation task.

3.1.2 Collaborative Computing Model

Generally,users need to subscribe ECS services from different operators to obtain edge computing services.However,due to the barriers of different operators and the limited computing capability of a single ECS,the subscribed users may not be served with guaranteed QoS,due to the nonuniform distribution of ECSs and burst traffci patterns during certain time at some specifci areas.To address this issue,collaborative edge computing is proposed by sharing the computing resources.Moreover,to attract the ECSs belonging to different third party or operators to participate in collaboration,proper incentive mechanism and mutual trust need to be guaranteed.We propose a blockchainbased cooperative MEC system,wherein each ECS joins the blockchain.When a user submits a task to the nearest server,the master node collects the task information,matches the user and the server.After that,master node packs the matching result into a transaction and broadcasts it to all participants to reach consensus.When the matching results are published,the user transmits the task to the matched server.The specifci process is as follows.

Initialization.Each user frist register to Certifciate Authority(CA)to get public key,private key,and certifciate: (pki,ski,certi).

Task request.The request information includes task information,timestamp,deposit,and location information.The request information of theith user can be expressed as:

whereDiis the task size,ciis the required CPU cycles of the task andRiis the reward provided by the user.Meanwhile,each ECS responses to the computing request with the following message

Task offloading and resource allocation.The primary node in consortium blockchain matches users and servers according toMSGreqandMSGresp,and record the results as a transaction:

Then primary node broadcasts the transaction on the chain for consensus.

Task execution and results return.After successfully offloading,user transfers the task to ECS.ECS returns the result to the primary node and useriafter executing the task.After results verifciation,the deposit will be returned to the user,users pays the reward to the server.

Given allocated resources of the ECS,the processing delay for the offloaded task of theith user is:

wherefijis the resources allocated touifromSj,ξis the coeffciient related to the data size of the task.

3.2 Problem Formulation

During the offloading process,the incurred delay includes: (i)the transmission timeto deliver the task data to ECS on the uplink;(ii)the processing timeto process the task at the ECS;(iii)the time to return the results from ECS back to the user on the downlink.Since the data size of the results is generally much smaller than the input,we omit the transmission delay of the output in this case,as has been assumed in[32].

According to the offloading decision of users,the total delay ofuican be written as:

Then the average delay minimization can be formulated as a joint task offloading(TO)and resource allocation(RA)problem,i.e.,

where constraints(10b)and(10e)imply that each task can be only offloaded to at most one server;constraint(10c)indicates that each ECS must allocate a positive computing resource to each user and(10d)shows the server’s computing capability constraint.

3.3 Consensus Mechanisim

In this sub section,we provide a computing contribution based mechanism to select consensus nodes.Then we present a primary node selection approach to avoid monopolization.

Selection of consensus node: Different from traditional consensus mechanism that all participants act as consensus nodes,we propose a reputation evaluation mechanism to select consensus nodes.The reputation values of each ECS reflect the QoS provided to users and the contribution in the task offloading consensus process[33],which can be calculated by:

wheretis the time slot,is the ECSSj’s reputation intth time slot,ρ ∈[0,1]indicates a weighting factor.Fereflects the ECSs’contribution,which is calculated by:

Lastly,ECSs with high reputation will be added into candidate pool and act as consensus nodes in the next round.

Completion time based primary node selection: We sort the nodes by their reputation value,and select the nodes with higher reputation as consensus nodes.In order to avoid the monopoly,we adopt the completion time based election of primaty node,that is the ECS with smallest response timein the last round will be selected as the primary node during this round.

IV.JOINT OFFLODING AND RESOURCE ALLOCATION ALGORITHM

Since the optimal problemP1 is a mixed integer nonlinear program,it is diffciult to fnid the optimal solution.We fnid that by fxiing the binary variablexij,P1 can be decomposed into multiple sub-problems with separated objective and constraints.Motivated by the approach in[32],we employ the Tammer decomposition method to transform the original problem into an equivalent master problem and a set of subproblems with lower complexity.SoP1 can be rewritten as:

4.1 Resource Allocation Algorithm

According to (9),the problem of resource allocation(14a)can be expressed as:

Thus,the Hessian matrix of the object function(15a)is a diagonal matrix,so the optimization problem in(15a)is convex optimization,which can be solved by using KKT optimal conditions.Denote the Lagrange function as:

One day the man said to his wife, I wonder, now, whether our parish clerk could teach Peter to talk; in that case we could not do better than adopt him as our son, and let him inherit all that we possess

Therefore,the optimal solution can be obtained by solving the KKT optimal-conditions,which is given as follows:

Whereλiis the Lagrange multiplier,constraint (19b)and (19c) are the primal and dual feasible conditions respectively.Moreover,(19d) represents the complementary slackness condition.

The frist derivation of(18)is:

when(20)equals to zero,we have:

4.2 Task Offloading Algorithm

In last subsection,we solve the optimal resource allocation problem for fxied offloading strategyxij.Since the TO problem is a NP-hard combinatorial optimization problem,it is diffciult to obtain the optimal solution in polynomial and only heuristic algorithm can be used to solve this kind of problem.In this paper,we adopt the NSGA-II algorithm.Since the network scale of MEC is smaller than that of traditional network,NSGA-II can reduce the solution space of the problem,which is suitable for solving the task offloading decisions.

Parameters initialization: The main parameters of NSGA-II are population sizeM,maximum iteration timesG,crossover probabilitypc,mutation probabilitypmand evolution termination condition.For the convenience of calculation,the number of individuals in each generation group is equal.The larger the group size is,the easier it is to fnid the optimal solution.However,due to the limitation of the computing power of the computer,the larger the group size is,the more time it takes to calculate.The termination condition of evolution refers to when the evolution ends.It can be set to the end of a certain generation of evolution,and it can also be determined by fniding out whether the approximate optimization meets the accuracy requirements.

Initial population: We need to generateMsequences as the initial population,and each iteration starts with a fxied initial population.Because there are many offloading strategies,we try to distribute users equally to the server according to the actual situation,so we initializeMpopulation according to the average distribution.

Fast non-dominated method: In this step,the population is stratifeid and all chromosomes are planned to different frontiers.The basis of stratifciation is the dominance level of chromosomes.

Crowding distance calculation: The defniition of crowding distance is that for the solutionϖi,the two nearest solutions with the vertex at the front of the motion are considered to form a rectangle,and the crowding distance of the solution isϖithe average side length of the rectangle.The specifci calculation formula of crowding distance is as follows:

wherelis the solutions of the same frontier,andare the maximum and minimum values of the objective function respectively.Crossover: Our crossing adopts single point crossing,which is designed as follows.For the elected two parentswe randomly select thetth gene as the intersection,the code of the offspring after cross operation iss1ands2.The gene ofs1is composed of the fristtgenes ofp1and the lastK-tofp2.Similarly,the gene ofs2is composed of the fristtgenes ofp2and the lastK-tofp1.We should choose a good crossover method as far as possible to ensure that offspring can inherit the good characteristics of their parents.

Mutation: Mutation is also a means to achieve population diversity,and it is also the guarantee of global optimization,the specifci design is as follows.According to the given mutation rate,we randomly selected three integers for the selected mutation individuals,which satisfy 1＜u ＜v ＜w ＜K.Then we insert the gene segment betweenuandv(includinguandv)afterw.

Election: We adopt a deterministic selection strategy,i.e.,select the individual with the smallest objective function value to evolve to the next generation,so as to preserve the excellent characteristics of the parent.

V.SIMULATION RESULTS AND DISCUSSION

In this section,we conduct simulations to verify the performance and effectiveness of our proposed scheme.

In the simulations,the parameters are fxied unless stated otherwise.We consider the network containing 20 mobile users and 5 ECSs,i.e.,K=20,N=5.Users are randomly distributed within a distance of 500m to 1500m from the ECS and the transmit power of each user is 20 dBm.The bandwidth allocated to each ECSBis 2MHz and the computing power of ECSsFjis [6,6,7,8,6] GHz.And we summarize the data sizeDi,task type,and the required CPU cycles of task in Table 1[34].By considering a Rayleigh fading channel model,the fading factor |hij|2obey a exponential distributionexp(1) and the path-loss exponentαis assumed to be 3.25.

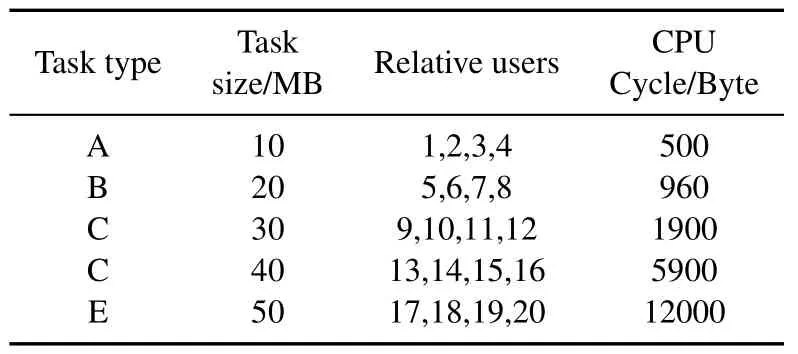
Table 1.Application complexity.

Note that 1000 Monte Carlo simulations are conducted for each curve.We compare the proposed algorithm with the other two methods,non-cooperative case and greedy algorithm.For the non-cooperative case: Users only offload tasks to the subscribed ECS.In our simulation,we assume that the frist four users with Type A tasks are subscribed to the frist ECS,the following 5-8th users with Type B tasks subscribe the second ECS,etc.Whereas the greedy algorithm based on the distance between the user and the server.The user will choose to offload the task to the nearest server for lower the transmission delay.

As explained in Section 4.2,we randomly select 100 chromosome of the initial iteration.Figure 2 shows that these individuals with different evolutionary starting points eventually evolved to the same result.

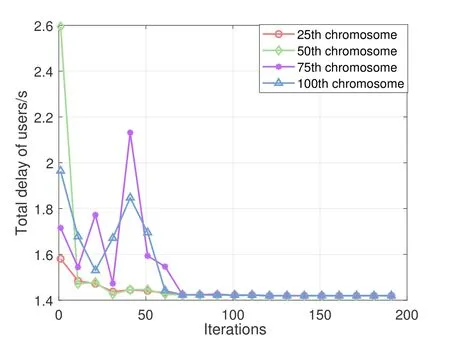
Figure 2.Convergence of NSGA-II algorithm.

We frist present the total delay of users versus the transmitting SNR with two comparison algorithm.As shown in Figure 3,the total delay has a tendency to reduce and converge with the increasing of transmission power of users for all algorithms because the increasing ofrijsignifciantly saves the communication delay then total delay is mainly composed with processing delay.The total delay of our proposed algorithm is much lower than the fxied assignment algorithm.

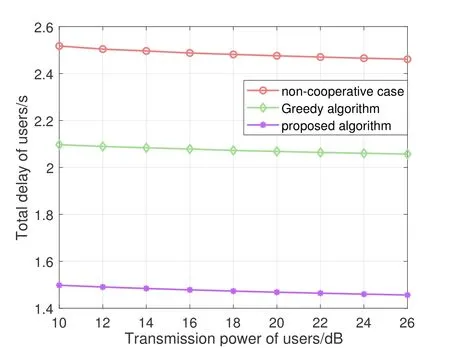
Figure 3.Total delay versus the transmission power of each user.

Similarly,to see the influence of users’task size on total delay,we set users’ task size follows uniform distributionU(30,100) MB.In Figure 4,as the average task size in the x-axis increases,the curves of three algorithms all show up upward trend.We can see that when the task size increases,the total delay of proposed algorithm increases slower than the delay of other two algorithms.

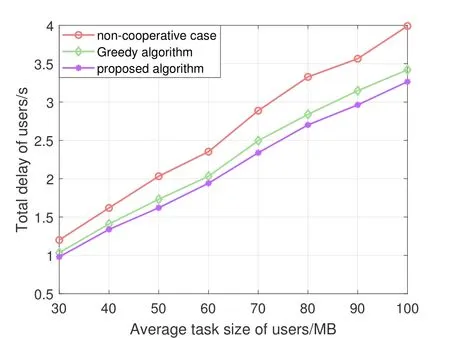
Figure 4.Total delay versus task size.

We also consider the capacity gap among ECSs and set different computing capacities in two cases.

Case 1.Represent the large resource gap,where the computing capacity of each ECS is F={2,2,2,2,20}[GHz].

Case 2.Represent the small gap,where we set Fclose={6,6,7,8,6}[GHz].

In case 2,Figure 5 and Figure 6 indicate the influence of the increasing computing capacity of single ECS and we setF5changes from 5 GHz to 50 GHz.In Figure 5,with the increase capacity of 5th ECS,three curves all decrease and the curves of“non-cooperative case” and “greedy algorithm” tend to converge.That is because when the capacity of 5th ECS is suffciient enough,the processing delay on it is negligible so that the total delay tends to unchanged.However,our proposed algorithm can allocate more users to 5th ECS,which saves more time compared to other two algorihms.Figure 6 shows the served user numbers of each ECS versus the computing capacity of the 5th ECS.We can see that with the increases of capacity,5th ECS tends to serve more than 50%of users in the system.

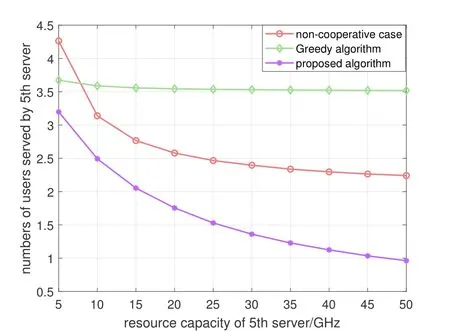
Figure 5.Total delay versus computing capacity of 5th ECS.

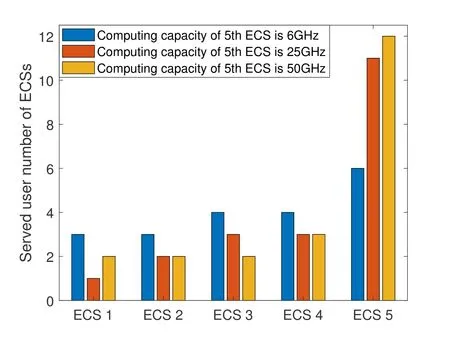
Figure 6.Number of users served by ECSs.

As shown in Figure 7,in non-cooperative case,when the resource gap is small,the time required is less than that the gap is large.In our proposed algorithm,it consumes less time when the gap is large.That is because in this case,the computing power of 5th ECS is high,and the proposed algorithm can allocate more users to 5th ECS to make better user of its computing capability.However,the non-cooperative case do not consider the current computing capacity of ECSs when matching users,which causes low eff-i ciency of the resource utilization.

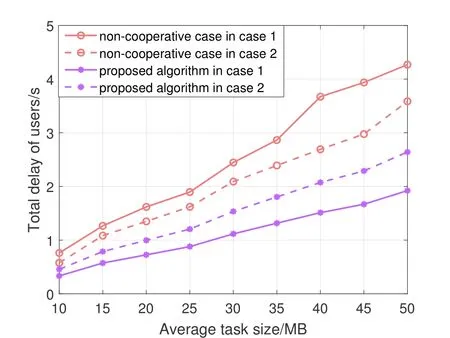
Figure 7.Influence of resource gap among ECSs.

Figure 8 compares the consensus times with CTPNS and the classic PBFT.Compared with PBFT,ECSs take less time to reach a consensus.We can observe that,the consensus time under CTPNS is much less than total delay of users,which is negligible in our proposed system model.

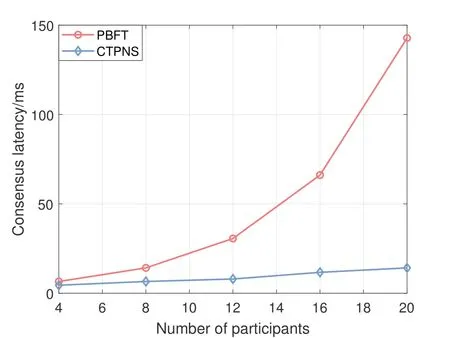
Figure 8.Consensus delay versus the number of participants.

VI.CONCLUSION

In this paper,we have proposed a consortium blockchain enabled collaborative edge computing framework,where multiple MEC servers cooperatively form a cluster to provide computing services with guaranteed QoS for end users and guaranteed revenues for servers.In order to minimize the average delay,we jointly optimize the task offloading and resource allocation with the computing constraints of each server.To solve the nonconvex optimization problem,we design an improved NSGA-II algorithm for task offloading and use KKT conditions to fgiure out the optimal resource allocation strategies.Simulation results verify we can see that the proposed framework is better than the conventional non-cooperative case in terms of fxied assignment and greed algorithm based matching performance.In addition,the proposed matching algorithm and resource allocation strategies outperform the common greedy algorithm and equal allocation algorithm.In the future,we prepare to investigate the cases of dynamic queuing and different types of resource requirements.

ACKNOWLEDGEMENT

This work was supported in part by the National Key R&D Program of China under Grant 2020YFB1005900,the National Natural Science Foundation of China under Grant 62001220,the Jiangsu Provincial Key Research and Development Program under Grants BE2022068,the Natural Science Foundation of Jiangsu Province under Grants BK20200440,the Future Network Scientifci Research Fund Project FNSRFP-2021-YB-03,and the Young Elite Scientist Sponsorship Program,China Association for Science and Technology.