A Support Data-Based Core-Set Selection Method for Signal Recognition

Yang Ying ,Zhu Lidong ,Cao Changjie

1 National Key Laboratory of Wireless Communications(University of Electronic Science and Technology of China),Chengdu 611731,China

2 College of Computer Science and Cyber Security(Chengdu University of Technology),Chengdu 610059,China

3 College of Mathmatics and Physics(Chengdu University of Technology),Chengdu 610059,China

Abstract: In recent years,deep learning-based signal recognition technology has gained attention and emerged as an important approach for safeguarding the electromagnetic environment.However,training deep learning-based classifeirs on large signal datasets with redundant samples requires signifciant memory and high costs.This paper proposes a support databased core-set selection method(SD)for signal recognition,aiming to screen a representative subset that approximates the large signal dataset.Specifcially,this subset can be identifeid by employing the labeled information during the early stages of model training,as some training samples are labeled as supporting data frequently.This support data is crucial for model training and can be found using a border sample selector.Simulation results demonstrate that the SD method minimizes the impact on model recognition performance while reducing the dataset size,and outperforms fvie other state-of-the-art core-set selection methods when the fraction of training sample kept is less than or equal to 0.3 on the RML2016.04C dataset or 0.5 on the RML22 dataset.The SD method is particularly helpful for signal recognition tasks with limited memory and computing resources.

Keywords: core-set selection;deep learning;model training;signal recognition;support data

I.INTRODUCTION

The rapid growth of satellite,wireless communications,and IoT technology has resulted in a dramatic increase in the number and diversity of wireless signals accessing the electromagnetic spectrum,seriously threatening the security of electromagnetic environments.Therefore,it is important to effectively identify or monitor these wireless signals.In recent years,deep learning has gained considerable attention and has been successfully employed for various signal recognition tasks like spectrum monitoring [1,2],interference identifciation [3,4] and outlier detection [5,6],establishing itself as a crucial tool in maintaining the security of the electromagnetic environment.

Most deep neural networks (DNNs) are trained on large datasets to reach advanced levels,which is extremely demanding in terms of memory and computation [7-12].Large datasets contain redundant samples,and pre-screening valuable ones can effectively reduce the training cost of recognition models.However,determining which samples are worth retaining and which ones should be removed is a challenging task for signal datasets.

Core-set selection technique has been widely used to identify a representative subset from a large dataset,and models trained on these subsets exhibit similar generalization performance to those trained on original datasets.Moreover,the work of [13-15] clearly pointed out that the training samples close to the decision boundary are very important to speed up the model convergence.The representative subset is a data subset that includes these important samples as the main body.However,the implicit nature of the decision boundary in DNNs makes it diffciult to directly fnid these samples that are located near the decision boundary.Therefore,many classical core-set selection methods[16,17]screen the representative subset by calculating various indirect parameters such as geometric properties or distances from class centers,but most of them require the use of a well-trained model.

In contrast,this paper proposes a novel support databased core-set selection method(SD)for signal recognition,which aims to screen a representative subset that can effectively replace the large signal dataset.The representative subset consists of those training samples that are frequently identifeid as support data during the early stages of model training.To this end,we employ a border sample selector to accurately label these support data.Experiments were conducted on the public RML2016.04C and RML22 signal datasets,and we replicated fvie other state-of-the-art core-set selection methods to adapt them for signal recognition tasks.The simulation results demonstrate that our SD method has a great competitive advantage,especially when the fraction of data kept is less than 0.3 on the RML2016.04C dataset or 0.5 on the RML22 dataset,our SD method outperforms fvie other advanced coreset methods.This innovative work can potentially benefti numerous applications with limited computing capabilities and memory.

The contributions of this paper are summarized as follows:

• We constructed a border sample selector to learn the knowledge of the output vector set from the signal classifeir,which accurately identifeis support data located near decision boundaries.

• We designed a strategy to evaluate the importannce of training samples by counting the frequency with which each sample is labeled as support data during the early stages of model training,in order to identify important samples for constructing a representative subset.

• We reproduced fvie other state-of-the-art core-set selection methods to adapt them for signal recognition tasks.

• Experimental results confrim that our SD method exhibits excellent performance.When the fraction of data kept is less than 0.3 on the RML2016.04C dataset or 0.5 on the RML22 dataset,it outperforms fvie other core-set selection methods.

The rest of this paper is organized as follows.Section II introduces the related work on core-set selection methods.Section III studies the principle of our SD method for the signal recognition task.In Section IV,a series of experimental results are employed to show the effectiveness of the SD method.Finally conclusions are drawn in Section V.

II.RELATED WORK

Many core-set methods have demonstrated the presence of redundant samples within large datasets,indicating the potential for further reduction in their size.Employing a smaller dataset can effectively mitigate the cost of model training.Prior research in this area can be broadly categorized into two aspects: synthetic sample generation and raw subset selection.

The former work distills the knowledge from the entire training set into a few synthetic samples generated by generative models like VAEs and GANs,which can serve as substitutes for the original training set in training recognition models.Representative research is dataset distillation [18-20].However,the training of generative models is diffciult and time-consuming.

The latter work employs various selection strategies to screen a valuable subset of the raw training set,thereby reducing its size.Representative research is active learning [15,21,22] and core-set selection[16,17,23-25].Some studies [13-15] have demonstrated the effectiveness of utilizing border samples in proximity to decision boundaries to accelerate model convergence,but fniding border samples directly remains challenging.Various core-set methods employed different indirect parameters to label border samples,including geometric properties[16],distance from class center[17]and gradient/disturbance change[15,25].For example,Max Welling[17]selected border samples based on their distance from the class center in the feature space.The larger the distance value,the further away the sample is from its corresponding class center and closer to the decision boundary.Ducoffe et al.[15] labeled border samples by generating adversarial samples,that is,converting the distance of each sample to the decision boundary into the amount of perturbation.The amount of perturbation added by changing the sample label is small,indicating its proximity to the decision boundary.All the aforementioned methods can effectively screen a representative subset by using a well-trained model,but they may encounter limitations when using an earlystage trained model.

At present,there are few core-set selection methods based on the early information of model training.Paul et al.[24] defnied the sample contribution for model training as the reduction in loss of all other samples on a single gradient step,and dynamically identifeid important samples during the early stages of model training.Furthermore,Toneva et al.[23]proposed that the model tends to forget samples near the decision boundary during training.Therefore,authors tracked the number of times a sample transitions from correct to wrong classifciation and selected important samples.Inspired by this,this paper proposes a novel support data-based core-set selection method for signal recognition.It evaluated the importance of each sample based on the information provided by the constructed border sample selector,which learned knowledge from the output vectors of the signal classifeir during the early stages of model training.Subsequently,samples were selected to construct the representative subset based on the importance.The detailed description is presented in the Section III.

III.A NOVEL CORE-SET SELECTION METHOD

This section presents the problem description of the core-set selection method for signal recognition tasks,followed by an elaboration on the model framework and the principle of our SD method.It concludes with a detailed exposition of implementation specifcis.

3.1 Problem Description

The development of communication and IoT technology has resulted in a signifciant increase in the signals that need to be identifeid in the electromagnetic environment.Therefore,pre-screening a representative subset for model training is important,as it can effectively reduce the size of large datasets while minimizing the impact on the model’s recognition performance.

Similar to [26],this work gives a large training set of raw signalsincludingKsignal classes,Nsignal samples andyis the signal sample’s corresponding label.Core-set selection technology aims to formulate a selection strategy to fnid the most valuable subsetfrom the large signal datasetDtrain,whereMis the size ofdtrain,M ＜＜N.The outputs of the model trained ondtrainare as near to the results of the model trained onDtrainas feasible.The raw signalx(t)can be formalized as[27,28]:

where,s(t)is the transmitted baseband signal,c(t)is the impulse response of the transmission channel,n(t)is the Additive White Gaussian Noise (AWGN),andx(t)represents the baseband wireless signal.

3.2 Support Data-based Core-Set Selection

In the early stages of signal classifeir training,this paper proposes a novel support data-based core-set selection(SD)method to identify a representative subsetdtrainfrom a large signal datasetDtrain.It involves two steps: labeling and screening.The principles behind these steps are explained in detail as follows.

3.2.1 Labeling Important Samples

The decision boundary of a DNN-based signal classifeir is implicit,posing challenges in directly identifying important samples near decision boundaries.To address this issue,we have constructed a border sample selector trained on the feature vector set of the signal classifeir to approximate decision boundaries and screen important samples.As shown in Figure 1,our used model framework consists of two key components: a signal classifeir and a border sample selector,which are described in detail below.

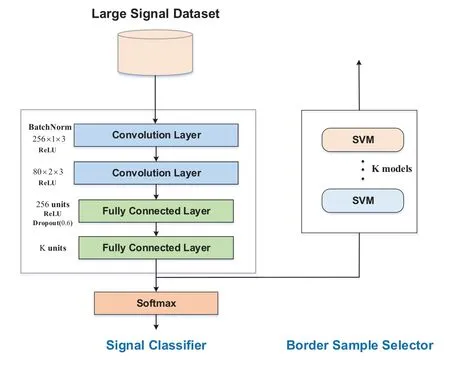
Figure 1.The schematic diagram of the used model framework.It consists of a signal classifier and a sample selector.

The DNN-based signal classifeir aims to extract the distinctive features of signals and generate accurate classifciation predictions.Here,its model architecture refers to the public signal recognition model VT-CNN2 in [29],which consists of two convolutional layers and two fully connected layers,each containing 256 convolution kernels and 80 convolution kernels respectively,and a ReLU activation function is introduced at the end of each convolutional layer.The two fully connected layers contain 256 andKneurons,respectively,whereKis the number of signal categories,and ReLU and Softmax are used as activation functions for the two fully connected layers,respectively.The Softmax activation function converts feature vectors into discrete probabilities.Specifcially,the feature vector set of the training samplesafter one SGD training of the signal classifeir can be written asZ=whereNis the number of training samples,ei=φ(xi),ei ∈R1×Tandw ∈RT×Kare thei-th input andi-th weight parameter of the classifeir’s last fully connected layer,Kis the classifeir’s output dimensions(number of signal classes).And thei-th output vector is converted by the Softmax function to as follows.

where,pi,kis the probability that a signal samplexiis predicted to be classzi,kis the output of thek-th node of the last fully connected layer,andwkis the weight of thek-th node of the last fully connected layer.

The cross-entropy loss is used as our signal classifeir’s optimization function,and it can be formalized as follows.

where,θis the parameters of the signal classifeir,NandKare the number of samples and categories in the signal training set,respectively,yi,kis a symbolic function,the value is 1 whenyi=k,otherwise the value is 0.

To screen important samples near decision boundaries,a border sample selector withKsupport vector machines (SVMs) has been constructed to learn the knowledge from the feature vector setZ=of the signal classifeir,as shown in Figure 2 and Figure 3.Since the feature vector set is linearly separable(see Figure 2(a)),this paper uses a simple linear SVM’s hyperplane equation to approximate the decision boundary between two classes of the signal classifeir (see Figure 2(b-d)),drawing inspiration from the work of [30,31].Following the one-vs-rest voting scheme[32,33],Kbinary-SVMs are used for constructing multi-class signal boundaries and labeling samples located near the decision boundary (see Figure 2(e)).

Figure 2.The schematic diagram of the inputs and outputs of the border sample selector. (a) input of the border sample selector,(b)-(d)results of three linear SVMs,(d)results of the border sample selector.

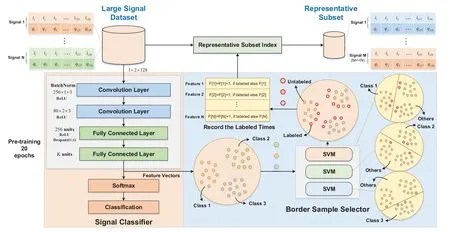
Figure 3.The flow chart of the support data-based core-set selection method for signal recognition.

The hyperplane equation of a linear SVM in the border sample selector can be written as follows.

where,ais the normal vector,which determines the direction of the hyperplane,bis the displacement,which determines the distance between the hyperplane and the training samplezi.The hyperplane equation is determined by the normal vectoraand the displacementb.

On this basis,the support vectorsT ≪Nin close proximity to the hyperplane can be found directly after the parametersaandbare solved.Each support vector (zi,yi) is the point that lies on the boundary of the maximum margin and meets the following criterion:

The margin is defnied as the projection of the difference between two classes of support vector ontoa,and the hyperplane is located in the middle of the margin.

However,in order to fnid the hyperplane with the largest margin,the parametersaandbneed to satisfy the following constraint:

Clearly,the training objective is to maximize the||a||-1,which is equivalent to minimizing||a||2.Thus the equation(6)can be rewritten as:

We set a slack variableξiand a penalty parameterCfor each training sample,the optimization problem of the border sanmple selector is to minimizeLs:

Here,after obtaining the optimal solutions foraandb,we approximately label the feature vectors located near the decision boundary by utilizing support vectors coordinate provided by equation (5).The important samples are the raw signal samples corresponding to these feature vectors.

3.2.2 Screening the Representative Subset

As signal classifeir training progresses,we have observed that some signal samples tend to appear in close proximity to decision boundaries and are frequently labeled as support vectors by our border sample selector.Similar phenomena are also described in[23].To this end,the authors defnied the concept of forgetting events for each training sample,and proved that training samples with a high frequency of forgetting events are important for effective classifeir training.Inspired by it,this paper proposes a novel selection strategy for screening a representative subset,and the implementation steps are as follows.

As shown in Figure 3,we frist record the frequency of each training sample labeled as a support vector during the 20 pre-training epochs of the signal classifeir,which serves as the basis for evaluating the importance of each training sample in signal clasiifeir training.Then,we sort all training samples in descending order based on their labeled frequency,with higher frequency values indicating greater importance for the signal classifeir.Finally,the representative subset consists of the fristMtraining samples,whereM=N*fandfis the kept fraction value,f ∈[0,1].More detailed explanations of our SD method is further elaborated in Algorithm 1.

We contend that the core idea of computing forgetting event statistics and computing labeled frequencies is consistent,as both rely on early model training information to fnid important training samples near decision boundaries.The distinction lies in our SD method to directly label these samples through a border sample selector.

3.2.3 Implementation Details

All experiments were conducted on two publicly available signal datasets RML2016.04C [34,35] and RML22 [36].The RML2016.04C dataset consists of three analog modulations and eight digital modulations,with each modulation corresponding to 20 SNR values ranging from -20dB to +18dB at intervals of 2dB.The data format of each signal sample is 1×2×128.The RML22 dataset contains two analog modulations (excluding AM-SSB) and eight digital modulations,with other parameters similar to the RML2016.04C dataset.A more detailed description is provided in[34,36].To mitigate the influence of noise on simulation results,we used signal samples within the SNR range of[+0dB,+18dB]to construct the experimental dataset.As a result,the RML2016.04C dataset utilized in this study comprises 51,040 signals,while the RML22 dataset includes 126,000 signals.Each modulation within each dataset is divided into a training set,validation set and test set in a ratio of 7:2:1 for subsequent experiments.

As previously mentioned in Figure 1,our SD method utilized a model framework consisting of a signal classifeir and a border sample selector.For the signal classifeir,we used the SGD optimizer with a learning rate of 0.001 and 0.01 (momentum=0.9,weight decay=5e-4) to perform 20 pre-training and 350 optimization training on both RML2016.04C dataset and RML22 dataset,while setting the batch size to 64.The border sample selector consists ofKlinear SVMs that are constructed using the SVC function from the Sklearn Library,with a penalty parameterCset to 0.9.All experimental results are averaged over fvie runs.

IV.EXPERIMENTS AND RESULTS

This paper proposes a novel support data-based coreset selection method for signal recognition,aiming to screen a representative subset from the large dataset in the early stages of model training.Therefore,simulation experiments are conducted in this section need to demonstrate the following aspects: The SD method can accurately identify training samples near the decision boundary,validate the effectiveness selected subset,and exhibit superior performance compared to fvie other advanced core-set selection methods.

4.1 Effectiveness of the Border Sample Selector

The implicit nature of decision boundaries in DNNs presents challenges for screening training samples located near the decision boundary.To address this issue,this paper proposes an innovative approach to train a border sample selector based on the feature vector set of the signal classifeir,which allows for direct labeling of important samples.Consequently,the frist experiment demonstrates the effectiveness of the border sample selector.

The multi-class border sample selector is extended from multi binary selectors based on the one-vs-rest voting scheme [32,33].For convenience,we conducted a simulation experiment on the training set consisting of the frist two modulations (8PSK and AMDSB)within the RML2016.04C dataset and presented the labeling result for the border sample selector,as shown in Figure 4.

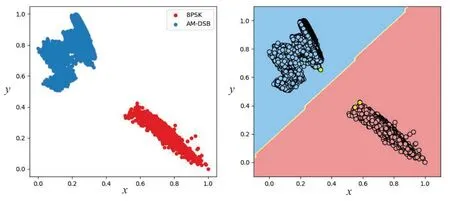
Figure 4.The visualization outcome of the important sample selection. Left: visualization of the output vector from the signal classifier. Right: visualization of the labeling result based on the border sample selector.

In the signal’s feature space,it is apparent that the border sample selector approximates the decision boundary of the signal classifeir as a linear function and effectively identifeis feature vectors (yellow data points) close to this boundary.These yellow data points correspond to raw signal samples labeled as important samples,providing evidence for the effectiveness of our SD method’s border sample selector in accurately identifying such signal samples.

4.2 The Representative Subset Selection

During the frist 20 epoch of model pre-training,we have observed that some signal samples frequently appear in close proximity to the decision boundary,leading our border sample selector labeling them as support vectors multiple times.In the second experiment,we fully utilized this information to identify training samples that are conducive to model training.

In the RML2016.04C dataset,we counted the number of times each training sample was labeled by the border sample selector during the frist 20 pre-training processes,as shown in Figure 5.It can be seen that the number of labeled times for each training sample is different during the early stage of model training,indicating that the occurrence frequency of each training sample near decision boundaries differs.We believe that such frequency information is closely related to the contribution made by training samples towards model learning.Particularly,some training samples(the dark blue and blue data points)have been labeled as border samples multiple times,and we posit that they hold greater signifciance in model training than others.

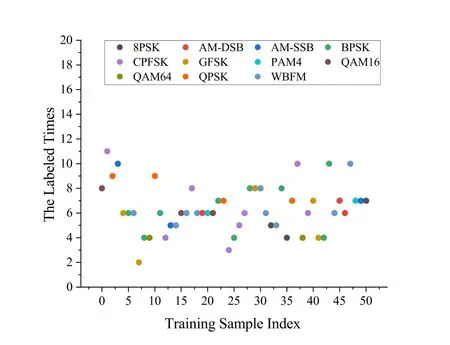
Figure 5.The labeled times of the first 50 training samples during the 20 pre-training epochs on the RML2016.04C dataset.

Additionally,we investigated the impact of varying pre-training epochs on the recognition accuracy of the signal classifeir for the RML2016.04C dataset.Given that only 30% of the training samples are retained,Figure 6 illustrates that increasing the number of pretraining epochs leads to higher recognition accuracy for signal classifeirs trained using selected representative subsets,indicating their greater value.It is in line with our expectations.In this paper,the pre-training epoch of the signal classifeir is set to 20.

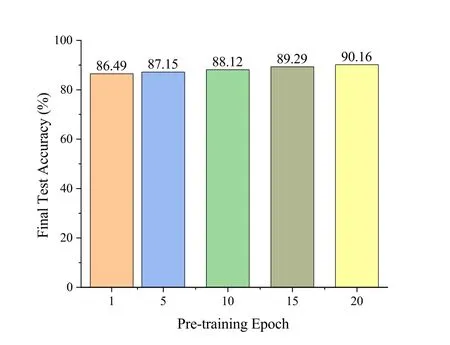
Figure 6.The influence of different pre-training epochs on the test accuracy of the signal classifier.

4.3 Compare with Other Core-Set Methods

To demonstrate the advantages of our SD method,we reproduced fvie other state-of-the-art core-set methods and adapted them for signal recognition tasks,as shown in Table 1.Subsequently,we compared the performance of our SD method with these advanced core-set methods on two publicly available datasets,RML2016.04C and RML22.‘No pruning’method utilizes the entire training set to train the signal classifeir,and it is anticipated that this method will yield the highest recognition accuracy.The methods of ‘Herding’ [17],‘DeepFool’ [15] and ‘Cal’ [37] require a well-trained classifeir for core-set selection,while the methods of‘Craig’[25]and‘Forgetting’[23]only require an early-stage trained classifeir to achieve coreset selection.

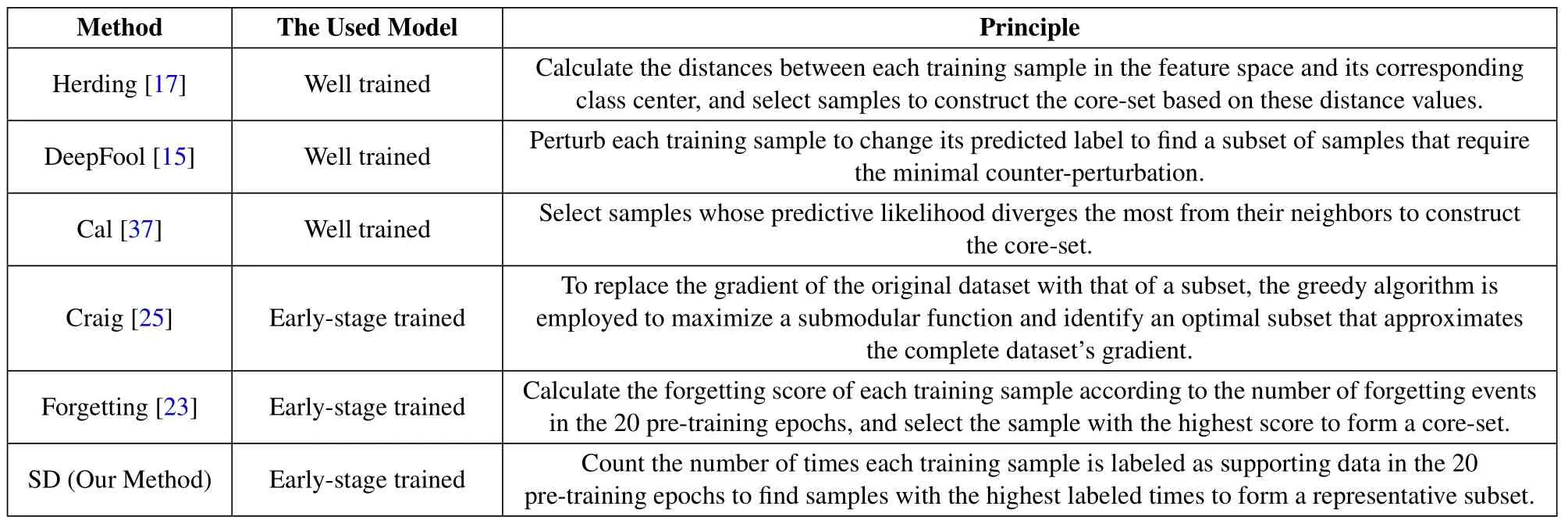
Table 1.Comparison analysis of the basic principles of different core-set selection methods.

In this paper,the VT-CNN2 model[29]is utilized as the signal classifeir,and the simulation experiment has the following settings.Specifcially,we recorded the gradient change,the number of forgetting events,and the number of labeled times for each training sample during the 20 pre-training epochs of the signal classifeir for ‘Craig’ [25],‘Forgetting’ [23],and our SD method.These metrics were used to evaluate the contribution of signal samples to classifeir training.This study focuses on selecting a representative subset for signal datasets during the early stage of model training to reduce dataset size and expedite subsequent training.Therefore,taking into account control variables,we employed the signal classifeir obtained after 20 pre-training epochs to replace the well-trained classifeir for executing core-set selection methods such as‘Herding’[17],‘DeepFool’[15],and‘Cal’[37].

In Figure 7,we compared the recognition performance of the signal classifeir after training on subsets with different sizes selected by various core-setselection methods.‘No pruning’ method exhibits superior recognition accuracy as anticipated,owing to its utilization of the complete signal training set and acquisition of comprehensive information.Its performance can be regarded as the upper limit for signal classifeirs to learn from current signal datasets.All other core-set selection methods have varying degrees of performance degradation as the fraction of data kept changes.In particular,the recognition performance of the‘Herding’[17],‘DeepFool’[15],and‘Cal’[37]methods is unstable due to their limited ability to leverage early-stage model training information for dataset screening.The recognition performance of the two dynamic screening methods,‘Craig’[25]and‘Forgetting’ [23],exhibits a gradual improvement as the fraction of data kept increases.Moreover,when the fraction exceeds 0.7 in the RML2016.04C dataset or surpasses 0.5 in the RML22 dataset,their performance closely approximates that achieved by the‘No Pruning’method.In contrast,the performance of our SD method outperforms other core-set selection methods on two distinct signal datasets,and it closely approaches the performance of ‘No pruning’ when the fraction is less than 0.3 in the RML2016.04C dataset or less than 0.5 in the RML22 dataset.This experiment clearly demonstrates the effectiveness of our proposed SD method.

Figure 7.Performance advantages of the proposed SD method on different signal datasets.

In addition,we demonstrated the performance advantages of the SD method by comparing the minimum training sample size required to achieve certain recognition accuracy requirements across different core-set selection methods as shown in Figure 8.The results depicted in Figure 8(a)-(b) demonstrate that,on the RML2016.04C dataset,the SD method uses the fewest training samples to achieve a recognition accuracy requirement of 85%or 90%.This indicates its superior ability to retain relevant information while eliminating redundant or irrelevant samples.It uses 22.7% (30.5%-7.8%) and 5% (35.5%-30.5%)fewer training samples respectively than the suboptimal‘Forgetting’method[23].Similarly,according to Figure 8(c),the SD method requires the fewest training samples to achieve an 80% recognition accuracy on the RML22 dataset.Remarkably,this method uses 23.9%(47.9%-24%)fewer training sample compared to the suboptimal ‘Forgetting’ method [23].In summary,the SD method is an excellent core-set selection method,especially when the fraction of training samples kept is low,which can quickly enable the signal classifeir to achieve good performance.

Figure 8.Comparison of training sample sizes required by different core-set selection methods.

V.CONCLUSION

In this paper,a novel support data-based core-set selection method is proposed for signal recognition,which can reduce the signal dataset size while minimizing the impact on signal classifeir’s recognition performance.This method is based on the premise that the important data points for model training are situated in close proximity to the decision boundary.Specifcially,fristly,we trained a border sample selector on the feature vector set of the signal classifeir to directly label important samples.Secondly,we observed that some training samples frequently appear in the support vector set during classifeir training.Based on this,we proposed a novel selection strategy to evaluate the importance of each training sample for model training.Finally,we utilized theMmost frequently labeled samples to construct a representative subset approximating the entire signal dataset.Experimental results on the public RML2016.04C and RML22 datasets have demonstrated that our SD method outperforms fvie other state-of-art coreset methods by effectively balancing the trade-off between reducing the size of the training set and maintaining high recognition accuracy of the classifeir model.Specifcially,to achieve the 85%recognition accuracy requirement on the RML2016.04C dataset,our SD method requires 22.7% less training samples than the fvie other advanced core-set selection methods.To achieve the 85%recognition accuracy requirement on the RML22 dataset,the usage of training samples is reduced by 23.9%.In addition,our SD method exhibits superior performance on the RML2016.04C dataset when retaining less than 0.3 of the data and on the RML22 dataset when retaining less than 0.5.It is suitable for signal recognition tasks in edge scenarios that prioritize limited memory and computation over high recognition accuracy.Future research could explore method’s specifci applications in edge scenarios or its potential utilization in memory-limited tasks,such as continual learning.

ACKNOWLEDGEMENT

This work is fully supported by National Natural Science Foundation of China (62371098),Natural Science Foundation of Sichuan Province (2023NSFSC1422),National Key Research and Development Program of China (2021YFB2900404),and Central Universities of South west Minzu University(ZYN2022032).