A Self-Attention Based Dynamic Resource Management for Satellite-Terrestrial Networks

Lin Tianhao ,Luo Zhiyong,2,*

1 School of Electronics and Communication Engineering,Sun Yat-Sen University,Shenzhen 518107,China

2 Peng Cheng Laboratory,Shenzhen 518107,China

Abstract: The satellite-terrestrial networks possess the ability to transcend geographical constraints inherent in traditional communication networks,enabling global coverage and offering users ubiquitous computing power support,which is an important development direction of future communications.In this paper,we take into account a multi-scenario network model under the coverage of low earth orbit (LEO)satellite,which can provide computing resources to users in faraway areas to improve task processing effciiency.However,LEO satellites experience limitations in computing and communication resources and the channels are time-varying and complex,which makes the extraction of state information a daunting task.Therefore,we explore the dynamic resource management issue pertaining to joint computing,communication resource allocation and power control for multi-access edge computing(MEC).In order to tackle this formidable issue,we undertake the task of transforming the issue into a Markov decision process(MDP)problem and propose the self-attention based dynamic resource management(SABDRM)algorithm,which effectively extracts state information features to enhance the training process.Simulation results show that the proposed algorithm is capable of effectively reducing the long-term average delay and energy consumption of the tasks.

Keywords: mobile edge computing;resource management;satellite-terrestrial networks;self-attention

I.INTRODUCTION

With the emergence of computation-intensive applications such as Internet of Remote Things (IoRT),military training and geological exploration,traditional terrestrial networks are increasingly unable to fulflil the requirements of ubiquitous transmission.This is primarily due to the inability to provide coverage in remote areas such as mountains,oceans,and deserts[1].Additionally,ground-based communication infrastructure is susceptible to factors such as typhoons,earthquakes,and conflicts.As a result,there is an increasing urgency for wireless networks that can provide long-term seamless coverage.Recently,signifciant developments in satellite-terrestrial networks have occurred,as seen by programs such as Starlink,which entail the deployment of numerous satellites to provide a wide range of services to commercial,civil,and military customers.Technology companies such as OneWeb[2],SpaceX[3],O3b[4],and TeleSat[5]have been actively launching satellites to offer communication services.Satellite communication offers several advantages over terrestrial networks,including more flexible network access services,extensive coverage,and enhanced capacity for backhaul [6].Notably,the utilization of low earth orbit(LEO)satellites equipped with edge servers enables them to serve as wireless edge access nodes within satellite-terrestrial networks,delivering both computing power and communication support to users.

On another front,the extensive advancement of hardware has resulted in the signifciant development of time-sensitive applications,including real-time gaming,intelligent transportation,high-defniition streaming media,and voice recognition [7].This has created a demand for satellites to not only offer communication services with global coverage but also services with low delay and high quality[8,9].Considering the limited resources of satellites,managing resources for computing and communication effciiently and reasonably is necessary [10].To reduce delay,users frequently prefer to offload tasks to the edge servers on LEO satellites rather than cloud servers.Wanget al.[11]presented a double edge computation offloading method for satellite-terrestrial networks to optimize latency and energy consumption,where terrestrial base stations and LEO satellites serve as edge nodes.Fanget al.[12] proposed a scheme based on many-to-one matching theory and game-theoretic to address the joint communication and computing resource allocation problem in satellite networks.In[13],the Orbital Edge Computing(OEC)task allocation algorithm was studied to reduce the computational cost.Authors in[14]introduced an effective computation architecture and proposed a distributed algorithm that utilizes the alternating direction method of multipliers (ADMMs) to effectively reduce the overall energy consumption of ground users.In [15],the minimization problem of the weighted sum energy consumption for terrestrial-satellite networks was decomposed into two layered subproblems and an energy effciient algorithm was proposed.However,most of the existing works employ conventional optimization algorithms to solve joint optimization problems,which necessitate numerous iterative solutions or cannot be generalized to complex scenarios.Thus,real-time guarantees cannot be ensured due to the algorithm’s substantial computational workload.

With this background,we consider a multi-scenario network model under the coverage of the LEO satellite with artifciial intelligence in this article,where users in different regions can offload tasks to the LEO satellite equipped with multi-access edge computing(MEC) server in order to minimize the energy consumption and delay of tasks.Although some deep reinforcement learning-based algorithms are proposed in [16-19],complex and time-varying satellite channel state information is still diffciult to analyze and extract features effciiently.To tackle this,we propose a self-attention based resource management algorithm,which can effectively enhance the feature extraction and learning process.To the best of our knowledge,this is the frist work that applies self-attention to the resource management problem in satellite-terrestrial networks.According to[20],the self-attention mechanism can capture the long-range dependencies and semantic relationships among the input vectors,and has been widely used in natural language processing and object detection.Moreover,it is effective in analyzing the state characteristics and requires signifciantly less time to train.By incorporating self-attention into the policy network and the Q network of the deep reinforcement learning framework,we can achieve superior performance in terms of delay and energy consumption.In general,we transform the original issue into a Markov decision process (MDP) problem and utilize a self-attention based resource management algorithm to jointly optimize the computing and communication resource allocation as well as power control.The key features of this paper are as follows:

• We propose a self-attention based resource management algorithm that jointly optimizes computing,communication resource allocation,and power control for satellite-terrestrial networks.This algorithm addresses the long-term delay and energy consumption issue caused by the uneven distribution of computing resources on the satellite to different users.

• Different from other algorithms based on deep reinforcement learning,the proposed self-attention based dynamic resource management (SABDRM) algorithm incorporates a self-attention mechanism into reinforcement learning.This mechanism is capable of effciiently extracting state features to expedite training and effectively address the MDP problem in high-dimensional continuous action and state spaces.

• According to the simulation experiments,SABDRM outperforms other baseline algorithms in terms of delay and energy consumption performance.

The remainder of this article is organized as follows.Section II introduces the system model and problem formulation.In Section III the SABDRM algorithm is proposed.Section IV discusses the simulation results.Finally,Section V concludes the article.

II.SYSTEM MODEL AND PROBLEM FORMULATION

The system model is represented in Figure 1 as a LEO satellite with a MEC server andNmobile users.We consider that users can offload tasks to the satellite in scenarios such as forests,deserts,cities,etc.There are two offloading modes for the users,namely local offloading and offloading to the LEO satellite.Based on the high-performance DRL-based mobile edge offloading scheme proposed in our previous work [21],we focus on resource management for each LEO satellite in this paper.Therefore,we only consider mobile users who offload their tasks to the satellite,presented byN={1,2,···,N}.Moreover,we useT={1,2,···,T}to denote all time slots,where each time slotthas durationτ[22].At each time slot,useri(i ∈N)generates a taskIi(t)={Li(t),Xi(t),Yi(t)},whereLi(t)denotes the computation amount of task,i.e.,the necessary CPU frequency required to fniish the task,andXi(t)represents the data size of the task[23].We denote the priority of the task asYi(t) andYi(t)∈Yis specifeid withY=[1,2,···,PN].The smaller the number,the higher the priority.The main notations used in this article are listed in Table 1.

Table 1.List of notations.

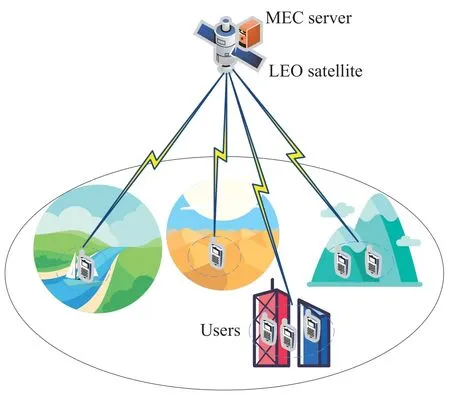
Figure 1.System model of multi-scenario communication under MEC-enabled satellite-terrestrial networks.

2.1 Communication Model

We assume that users adopt frequency division multiple access(FDMA)for their task offloading so that all users share the spectrum resources with a bandwidth ofB.According to the Shannon formula,the uplink rate from mobile userito the LEO satellite in time slottis:

whereβi(t)denotes the proportion of bandwidth allocated by LEO satellite to useriin time slott,piindicates the transmission power of useri,N0represents the Gaussian noise power spectral density.Considering shadowed-Rician fading as well as large-scale fading [24],the channel gain between the LEO satellite and useriis represented asgi.Specifcially,we havegi=G|li(t)|-ε,whereli(t) is the distance between LEO satellite and useri,Grepresents the antenna gain of useri,andεdenotes the path loss exponent[25].

Since the data size processed after the task is relatively much smaller than the size of input computation data,we do not consider the delay and energy consumption in downloading [26].Typical service types include statistics,machine learning,and data mining.Also,letcdenote the speed of light in vacuum,then the transmission delay of the task offloading to the MEC server is

The energy consumption associated with each user upload must not surpass the maximum energy capacity of its respective battery,so it should meet

2.2 Computation Model

Due to the users with different priorities accessing the LEO satellite and limited caching and computing resources on the LEO satellite,corresponding queuing delays may occur.Therefore,it is crucial to consider both the processing delay and the queuing delay of the task when a user offloads a task to the MEC server.For the edge computation,the computation delay consists of the processing delay and queueing delay.According to the above-mentioned,we defnie the CPU frequency of the LEO satellite asFand denote the computation delay of taskIion the LEO satellite as

whereκi(t) represents the proportion of computational resources allocated to taskIiby LEO satellite in time slott.When calculating the queuing delay,we introduce knowledge about queuing theory.Queuing theory has been extensively utilized in the feilds of communication and computing[27].There are several task queuesM(t)=[M1(t),M2(t),...,MN(t)]in the MEC server on the LEO satellite to store the arriving tasks,whereMi(t) denotes the computation tasks generated by useriexisting in the queue at time slott.It is assumed that the arrival rate of tasks of any priority at any time slot to the queues follows a Poisson distribution with parameterλi(t)[28],and the processing time of the MEC server follows an exponential distribution with parameterµ(t).Taking into account the accumulation of tasks in each queue caused by unfniished tasks at each time slott,it is necessary to consider the situation after the priority tasks arrive.To proceed,we assume that each non-preemptive f-i nite queue in the LEO satellite is an M/M/1 queue and tasks of the same priority are processed obeying the frist-come-frist-served principle.Furthermore,the MEC server has suffciient storage space to ensure that tasks will not be discarded by the queues.Based on the proposed model,there existPNpriorities,which will influence the total arrival rate as follows

Then the average queuing delay for taskIicorresponding to priorityYi(t)is

The remaining parameters are as follows

2.3 Problem Formulation

Based on the previous study,it can be clearly known that the overall delay for all computation tasks includes the delay of transmitting computing tasks to the LEO satellite and the computation delay of tasks on the LEO satellite.We choose the average energy consumption and the average delay of a task as the performance metrics in the dynamic resource management[29].The average cost function for all computation tasks in time slottcould be calculated according to(11),whereσ ∈R+is the cost coeffciient.

In edge computing systems,users have high requirements for both delay and energy consumption performance.Time-sensitive tasks with high priority demand lower delay,while users with small battery capacity require higher energy consumption performance on the users’ side.However,in practical scenarios,when the task with a large data size needs offloading to reduce the computation delay,the energy consumption as well as the transmission delay increase.To some extent,this means that reducing the computation delay of task results in increased transmission delay and energy consumption.Therefore,the cost function is formulated as (11) which trades off different performance measures by using the cost coeffciient.It can be found that the average cost can be derived as a function of transmission delay and computation delay.The cost to energy consumption and transmission delay ratio rises as the cost coeffciient increases,which has a greater impact on the system’s average cost.The optimization objective is to balance various performance measures based on users’requirements.

In order to solve the resource management problem of satellite-terrestrial networks with time-varying wireless channel states and randomly arriving tasks with different priorities,based on the aforementioned system model,we establish a joint computing,communication resource allocation and power control problem to optimize the total average cost for users.Specifcially,different tasks are processed in parallel within each time slot,but the delay and energy consumption between various tasks affect each other.Therefore,we propose the optimization objective:

The objective function (12) is to minimize the average cost in resource management over a period ofT.The frist constraint (13) limits the transmission power of useriduring time slott.Moreover,pminrepresents the minimum allowable transmission power,whilepmaxdenotes the maximum allowable transmission power.The second constraint(14) indicates that the energy consumption associated with each user upload can not surpass the maximum energy capacity of its respective battery.The third constraint (15) indicates the total amount of spectrum resources allotted to each user cannot exceed the total available bandwidth.The last constraint (16) states that the amount of computing resources allotted to different users by the LEO satellite cannot surpass the maximum amount of computing resources that the server itself can provide.The optimization problem can be formulated as a typical dynamic programming problem.In order to address this issue,we suggest making it a MDP framework,considering a fniite time horizonT.The solution method will be elaborated in the following subsection.

III.PROPOSED SELF-ATTENTION BASED SCHEME

In this section,we convert the problem (12) into a MDP problem and devise a self-attention based algorithm to solve it[16].

3.1 MDP-Based Dynamic Resource Management Problem

Suppose a MDP problem is a 4-element tupleM={S,A,P,R},whereSrepresents the state space,Adenotes the action space,P:S×A×S→[0,1]expresses the transition probability among all states,andR:S×A→R stands for the reward function.In every time slot,the agent will make a corresponding actiona(t)∈Abased on the current environments(t)∈S.The environment will then be updated tos(t+1)∈S,and the agent will receive a rewardr(t)from it for multiple cycles.Herein,we construct the MDP problem model in detail based on the above description.

(1) State Space: The agent receives the state informations(t)from the satellite communication environment at each time slott.

whereL(t)represents the amount of computation for all tasks,X(t)denotes the amount of data for all tasks,Y(t)stands for the priority of all tasks.E(t)andg(t)express the remaining battery energy information and wireless channel gain information of all users in time slott,respectively.

(2)Action Space: The agent makes the corresponding actiona(t)based on the currently observed information about the environments(t)every time slott.

wherep(t) expresses the users’ transmission power.β(t) andκ(t) indicate the proportion of bandwidth and computational resources allocated by the LEO satellite to all users at the current time slot,respectively.Specifcially,constraints (13),(14),and (16)specify the actions ina(t).

(3) State Transition Probability: The probability distribution ofs(t+1) givens(t) and the selecteda(t) are indicated by the state transition probabilityP(s(t+1)|s(t),a(t)).The probability distribution is only determined by the environment,and the agent does not have any prior knowledge of it[30].

(4)Reward Function: We defnier(t)as the reward function for performing actiona(t)in states(t).Generally,the MDP problem entails maximizing the cumulative reward function.However,our goal is to minimize the average cost from the optimization objective function(12)in this chapter.Therefore,based on the problem(12),we choose the opposite of cost as the reward function.Additionally,we defnie different reward functions depending on the constraints.At the time slott,the corresponding reward function is

When the restriction (13)-(16) are satisfeid,the reward function is the average cost under the time slott.If it is not satisfeid,we set the reward function to an extremely small value[16].Since the test periodTis generally large,it is guaranteed that-C(t)≫-TC(t)holds,making the model setup more scientifci.After converting the problem into a MDP problem,we will raise the self-attention based Soft Actor-Critic (SAC)framework.

3.2 Self-Attention Based SAC Framework

In the context of real-time resource management problems in large-scale user scenarios,the relationship between the inputs and the outputs of the environment state could be highly complicated,and extracting multidimensional features can be challenging.Traditional optimization methods often require a signifciant number of iterations,leading to the diffciulty of solving the real-time problem.In this paper,we propose a modifciation of the SAC based on self-attention as the underlying framework[31-33].In our module,there are three different types of neural networks: Policy network,Q network and Target network,the latter two of which are twins.As shown in Figure 2,they all use self-attention networks as nonlinear function approximators.Policy network takes the environment states(t) as its input and outputs actionsa(t) to the environment and Q networks.Actionsa(t) are the input to the Q network,which produces the soft Bell-Man residualto Policy network.Target network is used to slowly track the actual soft Q-function to improve stability.

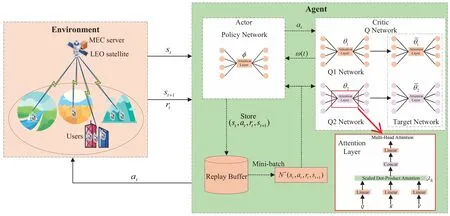
Figure 2.Self-attention based SAC framework.

3.2.1 SAC Framework

Reinforcement learning is usually used to solve tasks where the action and environment interact frequently,and SAC is a remarkable one to address both discrete and continuous control problems.In contrast to the conventional Proximal Policy Optimization(PPO)[34],SAC operates in an off-policy manner.This implies that it remains effective when faced with signifciant policy disparities,and offers enhanced sampling effciiency,allowing for the reuse of data generated from previous policies.Compared to Deep Deterministic Policy Gradient (DDPG) [35],SAC exhibits less sensitivity to hyper-parameters,rendering it more amenable to adjustments.Stochastic policy in SAC is accomplished through the utilization of maximum entropy which ensures that no valuable action or trajectory goes unnoticed and safeguards comprehensiveness in decision-making.SAC has a strong anti-interference ability and stable performance,using maximum entropy objective to develop a learning policy for increasingly diffciult work:

whereαis a hyper-parameter representing the temperature coeffciient,which is often utilized to fnie-tune the entropy value.In general,we seek a learnable policy moduleπ:S×A →R,which is able to direct the agent in selecting appropriate actions.And we employρπto represent the state-action marginals of the trajectory distribution brought on by a policyπ.Given a policyπand a states(t),we get the actionvalue function,also known as Q-functionQ(st,at)=to capture the anticipated cumulative reward when actiona(t)is chosen in states(t)according to the policyπ,whereγ ∈[0,1] is the discount factor.

In practice,action space typically contains vast continuous domains,necessitating the development of a realistic approximation to soft policy iteration.To that end,the algorithm constructs function approximation,which can be modeled as neural networksπϕ(at|st)andQθ(st,at) to describe policyπand action-state value functionQ(st,at).The actor-network and the critic-network are updated by evenly sampling the mini-batch from the replay buffer during each time step.In order to improve the stability and robustness of learning,SAC also utilizes a target network forQ(st,at) and policyπto perform soft updates based on the learned network.In the policy improvement step,the information projection described by the Kullback-Leibler divergence is favorable.To put it another way,we update the policy for each state during the policy improvement step according to

whereϱtrepresents an input noise vector,which is sampled from a predetermined distribution,such as a spherical Gaussian.The loss function for the actornetworks can be formulated as:

The gradient is as follows based on the mini-batch sample data:

Besides the actor-networks,the loss function for the critic-networks that can be trained to minimize the soft Bellman residual is:

The update incorporates a target soft Q-function,where the soft Q-function weights are averaged exponentially to determine the parameterswhich helps improve training stability.Furthermore,we parameterize two soft Q-functions with parametersθiand train them independently to optimizeJQ(θi) in order to eliminate positive bias during the policy improvement step.So we can approximate the gradient of(25)with

Along with the soft Q-function and the policy,we use the following formula to calculate gradients forα:

3.2.2 Self-Attention Mechanism

The preceding discussion focuses on the SAC framework.To provide a clearer explanation of our proposed algorithm,we will now introduce the multi-head self-attention mechanism [20].In the feild of machine learning,the attention mechanism is popularly used.In comparison to traditional DNN and CNN models,the attention mechanism not only reduces the number of model parameters but also enhances feature extraction capabilities.Furthermore,the attention mechanism enables the handling of variable-length sequences and multimodal information,enhancing the overall model’s flexibility and versatility.Specifcially,the attention mechanism model initially transforms the input into matricesQ,K,andVrepresenting a set of queries,keys and values,respectively.The output of the scaled dot-product attention can be formulated as:

wheredkis the dimension of queries and keys.Another benefciial way called multi-head attention is to linearly project the queries,keys and valueshtimes with various,learned linear projections todk,dkanddvdimensions,respectively.We simultaneously execute the attention function on each of the projected versions of the queries,keys,and values.Laterdvdimensional output values can be produced.The fnial values are created by concatenating the output values and then projecting them once again.The multi-head attention mechanism enables the model to simultaneously focus on various subspaces of information at different positions.The output of the multi-head selfattention is:

3.3 Practical Algorithm

Based on the self-attention mechanism and SAC framework,we propose the SABDRM algorithm.SABDRM algorithm is an offline algorithm and utilizes the stochastic policy of maximum entropy to explore more possibilities.As an offline algorithm,SABDRM requires multiple episodes of iterations,each of which consists of an environmental step and a gradient step.At the end of the last episode,the agent will make a real decision.

During each episode,the agent takes actiona(t)based on the current policyπϕ(at|st) and the collected states(t) for each environment step.After getting an actiona(t),the system environment provides the agent with the next states(t+1) and rewardr(t),according to the state transition probabilityP(s(t+1)|s(t),a(t)).The agent then stores the transition in the replay buffer for further learning and decision-making.

For each gradient step,two Q networks and the policy network update their model parametersθiandϕby sampling mini-batches of dataN*(s(t),a(t),r(t),s(t+1)) from the replay buffer,respectively.After that the system updates the temperature coeffciientαand target network weightsBy iterative sampling and updating the model parameters with the replay buffer,the policy network and the Q networks gradually improve their performance and learn to make better decisions in the given environment.

In contrast to conventional deep reinforcement learning,the policy network and Q networks in SABDRM employ a network with the multi-head selfattention mechanism rather than DNN.This facilitates enhanced extraction of features from the input vectors,as demonstrated in Section IV through experimental simulations.

The fnial algorithm is presented in Algorithm 1.In practice,we take one gradient step after a single environment step.The approach involves an iterative process of gathering experience from the environment and updating the function approximators.Additionally,the former uses the current policy and the stochastic gradients from batches sampled from a replay buffer are utilized by the latter.

IV.SIMULATION RESULTS

In this section,we conduct a series of simulation experiments to evaluate the performance of the SABDRM algorithm in satellite-terrestrial networks,which is shown in Figure 3 to Figure 9.To facilitate the comparison,the average cost is applied in the baselines including the DDPG scheme,random resource management (RRM) scheme and uniform resource management(URM)scheme.

Figure 3.The convergence curve of different schemes.

• DDPG scheme: The deep reinforcement learning algorithm DDPG is an actor-critic,modelfree algorithm that operates over continuous action spaces and is based on the deterministic policy gradient.

• RRM scheme: Its basic thesis is that the MEC server randomly assigns the spectrum resource and the computing resource to each task.Moreover,each user’s transmission power is random.

• URM scheme: For URM,the MEC server evenly allocates computing resources and spectrum resources to each user.The transmission power of each user is the average of the upper and lower power limits.

We compare the average cost of the proposed SABDRM algorithm with the three baselines in terms of the computation amount of task,the data size of task,the number of priority levels of task,the total computing capacity of the LEO satellite and the number of users.

4.1 Experiment Setup

Simulation is performed on Python 3.9.We set up the LEO satellite with an altitude of 784 km flying across a square area of 1200 m × 1200 m [36],and ground users with different priorities randomly distributed.In addition,the channel information can be obtained in advance by the sensing technique.

In the simulation,we set the channel bandwidth to 20 MHz with the Gaussian noise power spectrum densityN0=-174 dBm/Hz,and the channel model is chosen as shadowed-Rician fading as well as largescale fading channel model mentioned above.We mainly consider the computation amount,data size,priority,and possible energy consumption for the task parameters.The minimum limit of transmission powerpminis 23 dBm and the maximum limitpmaxis 38 dBm,according to[37].Besides,we assume a user’s maximum battery capacity is 1000 J[16]and the totalcomputing capacity of the LEO satellite is taken fromU[15,35]GHz.

In the SABDRM algorithm,we use the multi-head self-attention network instead of DNN as the feature extraction layer of deep reinforcement learning followed by a flatten layer.What remains constant is that both the input and output layers are DNNs.After careful adjustment,we employh=8 heads.The characteristic dimension of the output is 256,and the dropout rate is 0.The training parameters of the model have a discount of 0.99.In addition,the main parameter settings are detailed in Table 2.

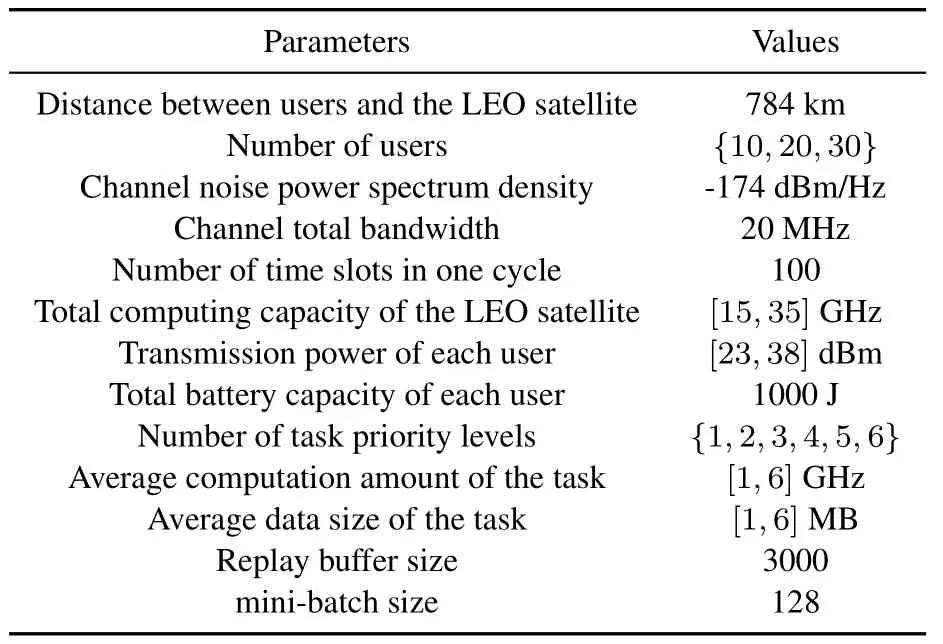
Table 2.Experiments parameters.

4.2 Performance and Analysis

Figure 3 shows the convergence curves of different reinforcement learning algorithms.The learning rate is set as 10-3.It can be seen in Figure 3 that the proposed SABDRM has better performance than DDPG.Specifcially,the average cost of SABDRM can obtain 3 after 50 episodes.In contrast,the average cost of DDPG fluctuates around 5 after 175 episodes.This comparison proves that the benefti of the selfattention mechanism can better extract state features to speed up training and solve the MDP problem in high-dimensional continuous action and state spaces effectively.

Figure 4 illustrates the average cost of users for the four algorithms with varying computation amounts of task.The number of priority levels of task and the number of users are set to 3 and 10,respectively.The data size of task and the total computing capacity in the LEO satellite follow Gaussian distributions with mean values of 3.5 MB and 25 GHz,respectively.Figure 4 denotes that the average task cost increases as the computation amount increases.The underlying explanation lies in that,with a fxied total computation capacity on the satellite,an increased computational load per offloaded task results in elevated delay and energy consumption.Consequently,this leads to a higher average cost across the entire system.Moreover,the average cost of the SABDRM is lower than the counterparts of the other three baselines.In particular,SABDRM effectively mitigates cost by 53.7%,48.6%,and 29.6% when compared to RRM,URM,and DDPG,respectively.

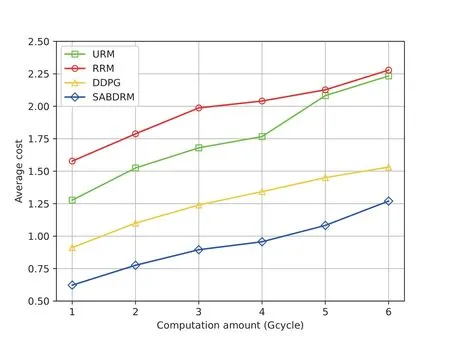
Figure 4.Average cost of ground users versus different computation amount of task.

Figure 5 depicts the average cost of task for URM,RRM,DDPG and SABDRM versus different data sizes.Here the number of priority levels of task and the number of users are set to 3 and 10,respectively.The computation amount of task and the total computing capacity in the LEO satellite follow Gaussian distributions with mean values of 3.5 Gcycles and 25 GHz,respectively.It can be observed from Figure 5 that the average cost of task increases with the data size.According to equation(2)-(4),the maximum battery capacity of the users limits the transmission energy consumption.Consequently,the average delay increases along with the data size of task,resulting in a rise in average cost.Furthermore,the proposed SABDRM performs better than RRM,URM and DDPG,which can effectively lower the average cost of task by 54.3%,46.4%,and 26.6%,respectively.

Figure 5.Average cost of ground users versus different data size of task.

Figure 6 shows the average cost of task the four algorithms with different numbers of priority levels of task.The number of users in this fgiure is set to 10.The computation amount of task,the data size of task and the total computing capacity in the LEO satellite follow Normal distributions with mean values of 3.5 Gcycles,3.5 MB and 25 GHz,respectively.The larger number of priority levels of task leads to higher queuing delay,which can increase the average cost of task.In addition,on average,the proposed SABDRM algorithm can reduce the average cost of task by 52.5%,50.1%and 29.7%compared with RRM,URM,and DDPG,respectively.The decisions created by RRM exhibit substantial uncertainties and are likely not optimal because of the randomness of RRM.Consequently,the trajectory of RRM tends to fluctuate.When the number of priority levels of task is large,URM will bring greater cost.The reason is that the impact of task priorities is ignored,which results in serious queuing delay.

Figure 6.Average cost of ground users versus different number of priority levels of task.

In Figure 7,we frist conduct a comparative analysis of the cost performance achieved by different resource management algorithms under varying total computing capacities of the LEO satellite.Each point in the fgiure represents the average performance across 1,000 independent wireless channel realizations [17].Here the number of priority levels of task and the number of users are set to 3 and 10,respectively.The data size and computation amount of task follow Gaussian distributions with mean values of 3.5 MB and 3.5 Gcycles,respectively.We see that the proposed SABDRM algorithm performs noticeably better than the other three baselines.In Figure 8,we further compare the cost performance of SABDRM and DDPG algorithms based on deep reinforcement learning.For better exposition,we plot both the median and the confdience intervals of average cost over 1,000 independent channel realizations.Specifcially,the central mark,highlighted in red,signifeis the median,and the bottom and top edges of the box represent the 25th and 75th percentiles,respectively.We fnid that the less the total computing capacity of the LEO satellite,the longer the average cost of the task.The increased total computing capacity signifeis that,on average,the LEO satellite possesses the ability to allocate a greater amount of computing power to each user,thus diminishing the average cost of task.Moreover,it can be observed that the median of the SABDRM algorithm is always lower than the counterpart of the DDPG algorithm and the upper and lower quartiles of SABDRM are spaced less than the DDPG,which means the deviation of the proposed SABDRM is smaller.As shown in Figure 7 and Figure 8,the SABDRM can reduce 32.1%of the average cost compared to the DDPG scheme.In contrast to the RRM and URM schemes,the SABDRM can reduce 54.8% and 48.6% of the average cost,respectively.

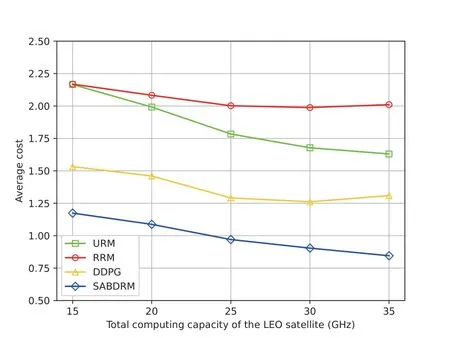
Figure 7.Average cost of ground users versus different total computing capacity of the LEO satellite.

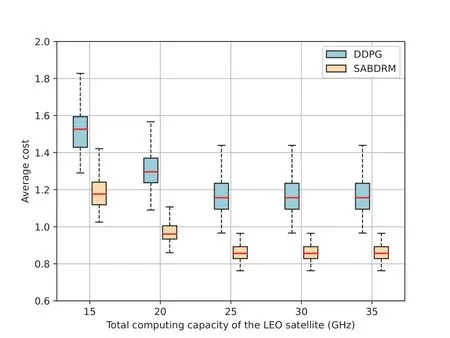
Figure 8.Boxplot of the average cost of ground users for DDPG and SABDRM algorithms under different total computing capacity of the LEO satellite.

Figure 9 fnially contrasts the average cost of users for the four algorithms versus various numbers of users.Here the number of priority levels of task is set to 3.The computation amount of task,the data size of task and the total computing capacity in the LEO satellite follow Normal distributions with mean values of 3.5 Gcycles,3.5 MB and 25 GHz,respectively.It can be observed that the average cost of task increases with the number of users.This phenomenon occurs due to the diminishing allocation of spectrum resources and computing power resources to each user as the number of users increases,consequently resulting in heightened delay and energy consumption.As shown in Figure 9,the SABDRM can reduce the average cost of task by 30.9%,17.4%and 10.1%compared with RRM,URM,and DDPG,respectively.

Figure 9.Average cost of ground users versus different number of users.

V.CONCLUSION

In this paper,we have investigated the optimization problems of joint computing,communication resource allocation and power control between satelliteterrestrial networks.To address the dynamic and complex nature of satellite channels,the problem was converted to a MDP problem.Due to the large dimension of channel state in satellite-terrestrial networks and the challenge of feature extraction,we proposed the SABDRM algorithm based on the self-attention mechanism,which optimized the energy consumption and long-term average delay under the condition of limited computing power resources of LEO satellite and battery capacity of users.Extensive experimental results presented that,when compared to other baseline algorithms,our proposed algorithm showed superior performance in terms of reducing the average cost of users.Our work can offer valuable insights for future research on computing resource allocation for satellite-terrestrial networks and deep reinforcement learning algorithms.In the future,we will further explore collaborative resource management among satellites,effciient communication methods and mobility management in satellite-terrestrial networks,involving information theory and online optimization techniques.

ACKNOWLEDGEMENT

This work was supported by the National Key Research and Development Plan(No.2022YFB2902701)and the key Natural Science Foundation of Shenzhen(No.JCYJ20220818102209020).