A Synchronization Acquisition Algorithm Based on the Frequency Hopping Pulses Combining

She Honghan,Cheng Yufan,Zhang Wenzihan,Zhang Yaohui,Zhao Yuheng,Shen Haoran,Mou Ying

National Key Laboratory of Wireless Communications,UESTC,Chengdu 611731,China

Abstract: As modern electromagnetic environments are more and more complex,the anti-interference performance of the synchronization acquisition is becoming vital in wireless communications.With the rapid development of the digital signal processing technologies,some synchronization acquisition algorithms for hybrid direct-sequence (DS)/frequency hopping (FH)spread spectrum communications have been proposed.However,these algorithms do not focus on the analysis and the design of the synchronization acquisition under typical interferences.In this paper,a synchronization acquisition algorithm based on the frequency hopping pulses combining (FHPC) is proposed.Specif-i cally,the proposed algorithm is composed of two modules: an adaptive interference suppression (IS) module and an adaptive combining decision module.The adaptive IS module mitigates the effect of the interfered samples in the time-domain or the frequencydomain,and the adaptive combining decision module can utilize each frequency hopping pulse to construct an anti-interference decision metric and generate an adaptive acquisition decision threshold to complete the acquisition.Theory and simulation demonstrate that the proposed algorithm signifciantly enhances the antiinterference and anti-noise performances of the synchronization acquisition for hybrid DS/FH communications.

Keywords: adaptive anti-interference;frequency hopping;synchronization acquisition

I.INTRODUCTION

Modern military data links face a complex and changing electromagnetic environment and various interferences,and the anti-interference capability of wireless communications determines the key to battlefeild victory [1].Hybrid direct-sequence (DS)/frequencyhopping (FH) spread spectrum system,as one of the representatives of tactical data links,enhances the anti-interference capability of the data links and guarantees the reliable data transmission[2].

Synchronization acquisition is a critical part of all communication systems and is the key factor affecting the transmission performance.However,the performance of the synchronization acquisition under typical interferences will be seriously deteriorated [3-6].Therefore,how to improve the anti-interference performance and the robustness of the synchronization acquisition is one of the research focuses of hybrid DS/FH communications.

The conventional synchronization acquisition algorithms focus on the DS spread spectrum systems,i.e.,the serial or parallel acquisition is accomplished based on the correlation peaks in the spread spectrum code domain.A novel acquisition algorithm based on the simultaneous search of the code phase and the Doppler frequency was proposed in [7],which reduces the effect of the frequency offset by updating the local frequency offset compensation parameter in real time through the non-coherent accumulation of the pseudo random code correlation values.A noncoherent data/pilot combined acquisition algorithm was proposed in [8] and it derives the theoretically detection threshold through the constant false alarm rate(CFAR)criterion,which improves the acquisition probability at low signal-to-noise ratio (SNR).Reference [9-11] analyzed the performance of the partial matched flitering-fast Fourier transform (PMF-FFT)algorithm,which uses the FFT results of the partial sequence correlation values as the detection variables to enhance the anti high dynamic capability.However,such algorithms are not applicable to the hybrid DS/FH communications,where the random phases introduced by the frequency hopping can severely deteriorate their performances.

The synchronization acquisition algorithms for the hybrid DS/FH communications are mainly designed based on the frequency hopping pattern.A two-level acquisition algorithm based on the differential correlation peaks was proposed in [12],which enhances the performance of the synchronization acquisition in high dynamic environments through the joint detection of the pseudo random sequence and the frequency hopping pattern.A 3-dimensional search-based synchronization acquisition algorithm was proposed in [13],which improves the SNR performance at the expense of hardware complexity by searching in the hopping frequency-domain,the spread spectrum code domain,and the Doppler domain.Reference[14]proposed an acquisition algorithm based on the binomial decision of the frequency hopping pulses,which utilizes the detection results of all pulses in the frequency hopping pattern for counting decision to improve the noise tolerance of hybrid DS/FH communications.However,such algorithms do not focus on the design and the analysis of the synchronization acquisition algorithm under typical interferences.

In order to optimize the anti-interference performance of the synchronization acquisition algorithm under typical interferences,a synchronization acquisition algorithm for hybrid DS/FH communications based on the frequency hopping pulses combining(FHPC),is proposed in this paper,and this algorithm can adjust the non-coherent combining coeffciients according to the interference power of each frequency hopping pulse and generate the adaptive acquisition decision threshold,which signifciantly improves the anti-interference performance of the synchronization acquisition for hybrid DS/FH communications under typical interferences.The main contributions of this paper are summarized as follows:

1) The FHPC-based synchronization acquisition algorithm has been proposed.Specifcially,the proposed algorithm is composed of two key modules:an adaptive interference suppression(IS)module and an adaptive combining decision module.The adaptive IS module mitigates the effect of the interfered samples in the time or frequency-domain,and the adaptive combining decision module can utilize each frequency hopping pulse to construct an anti-interference decision metric to complete the acquisition.

2) The adaptive acquisition decision threshold of the proposed FHPC-based algorithm has been derived theoretically.The adaptivity reflects that the threshold can be applied to both the pulse-noise interference (PNI) scenario and the narrow-band noise interference (NBNI) scenario,and can accomplish the acquisition with constant false alarm probability under different interference parameters.

3) The numerical results of the proposed FHPCbased algorithm under the PNI or the NBNI have been given,respectively.The simulation results verify the correctness of the theoretical derivation and demonstrate that the proposed FHPC-based algorithm enhances the anti-interference and antinoise performances of the synchronization acquisition for hybrid DS/FH communications under the PNI or the NBNI.

The rest of this paper is organized as follows.Section II describes the system model.Section III elaborates the proposed FHPC-based algorithm,and derives the adaptive acquisition decision threshold and the acquisition performances under two types of interferences.Section IV conducts extensive experiments and validates the effectiveness of the proposed algorithm.Finally,Section V gives the conclusion of this paper.

II.SYSTEM MODEL

2.1 Transmitted Signal Model

Figure 1 shows the frequency hopping pulses structure of the synchronization segment[15].As shown in the fgiure,the synchronization segment has a total of 40 frequency hopping pulses distributed at 8 frequencies,with 32 pulses in the coarse synchronization segment for the synchronization acquisition and 8 pulses in the fnie synchronization segment for the synchronization tracking.Note that there are 6.4us for transmitting the minimum shift keying(MSK)waveform in each pulse,and the remaining 6.6us is a silent period.

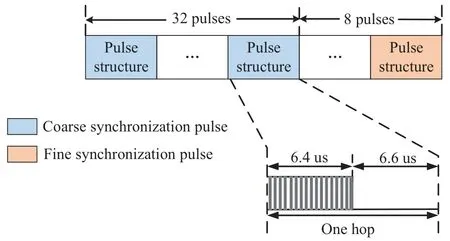
Figure 1.The frequency hopping pulses structure of the synchronization segment.

Assuming that all chips within 6.4 us within a pulse are modulated with MSK,the baseband signal form of thel’th pulse at the hopping frequencyfican be expressed as

2.2 Interference Signal Model

The PNI is a typical time-domain interference and the baseband signal form of thel’th pulse of the PNI can be modeled as

whereJPNIl[n] denotes the symbol-level samples of thel’th pulse of the PNI.denotes the index set of the interfered time-domain samples,and the number of the elements ofdenotes the average interference power of the PNI.

The NBNI is a typical frequency-domain interference.Since the baseband samples of the NBNI can be regarded as complex additive white Gaussian noise(AWGN)samples passing through a narrow-band lowpass fliter,the baseband signal form of the NBNI at the hopping frequencyfican be modeled as

2.3 Received Signal Model

Since the transmitted signal is distributed at 8 hopping frequencies,the received signal are processed in parallel at the 8 hopping frequencies.Therefore,the received symbol-level samples matrix at the 8 hopping frequencies can be formulated by

wherey(fi)denotes the received symbol-level samples at the hopping frequencyfi.denotes the received symbol-level samples of thel’th pulse at the hopping frequencyfi,andLdenotes the number of the coarse synchronization pulses in Figure 1.

Tactical military network is strictly the line-of-sight(LOS) communication system [14],and the largescale fading is dominant,which can be compensated by power control[16].Therefore,the single-path Rician channel is selected in our model,and the channel matrix can be formulated by

The hybrid DS/FH system introduces a initial frequency offset during the down-conversion and a random phase at each hopping frequencyfiduring the frequency hopping and de-hopping.Therefore,the phase offset vector can be formulated by

whereΦ(fi)denotes the phase offset matrix at the hopping frequencyfi.Δfdenotes the initial frequency offset.Rsdenotes the modulated symbol rate.θ(fi)denotes the random initial phase at the hopping frequencyfiand it satisfeisθ(fi)～U[0,2π].

From (5)-(7),the received symbol-level samples at the hopping frequencyfiover a single-path Rician channel with a typical interference can be modeled as

wherex(fi)denotes the transmitted pulses in the synchronization segment at the hopping frequencyfi.J(fi)andw(fi)denote the interference samples and the complex AWGN samples at the hopping frequencyfi,respectively.Assuming thatanddenotes the average noise power.

III.THE PROPOSED SCHEME

In this section,the FHPC-based synchronization acquisition algorithm is proposed,which is composed of two modules: an adaptive interference suppression(IS)module and an adaptive combining decision module.Moreover,the adaptive acquisition decision threshold and the acquisition probabilities of the proposed algorithm under the PNI or the NBNI are derived theoretically,respectively.

3.1 The Structure of the Proposed Algorithm

The overall structure of the proposed FHPC-based algorithm is presented in Figure 2.As shown in the fgiure,the transmitter modulates the synchronization sequence with MSK and then generates the frequency hopping pulses in the synchronization segment,whose frequency hopping pattern is arranged cyclically according to the hopping frequencies{f1,...,f8}.

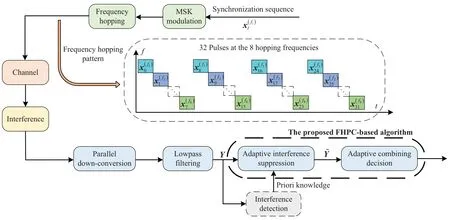
Figure 2.The overall structure of the proposed FHPC-based algorithm.

Correspondingly,the received symbol-level samples matrix,i.e.,Yin (5),at the 8 hopping frequencies is obtained after the parallel down-conversion,parallel lowpass flitering and parallel down-sampling.Note that the input to the FHPC-based algorithm is Y,and the proposed algorithm is composed of two modules:the adaptive IS module and the adaptive combining decision module.Specifcially,assuming that the receiver has some priori knowledge about the interference,e.g.,the interference type,and the average interference power,the adaptive IS module multiplies weighting factors on the interfered samples in the time or frequency-domain [17],which can reduce the deterioration of the interference on the received pulses.The adaptive combining decision module extracts the 32 pulses according to the transmitted frequency hopping pattern in Figure 1 to construct the noncoherent weighted combining metric,and generates the adaptive acquisition decision threshold to complete the acquisition decision.

3.2 The Proposed Algorithm Under the PNI

In general,the synchronization acquisition problem can be simplifeid to a binary hypothesis testing problem.Assuming thatH1denotes the hypothesis that the pulses in the synchronization segment have been sent from the transmitter,andH0denotes the hypothesis that the pulses in the synchronization segment have not been sent from the transmitter,the received symbollevel samples in(8)can be rewritten as

As shown in (2),the PNI can be regarded as the complex AWGN on the interfered time-domain samples.Therefore,a set of IS coeffciients are multiplied by the interfered time-domain samples in the adaptive IS module of the proposed FHPC-based algorithm,which can reduce the average interference power of the interfered samples,and the symbol-level samples of thel’th pulse at the hopping frequencyfiafter the interference suppression can be expressed as

From (10)-(12),the effect of the adaptive timedomain IS for the PNI is shown in Figure 3.As shown in the fgiure,since the system discussed in this paper is the hybrid DS/FH system,the SNR of the received symbol-level samples is low,i.e.,the signal is annihilated in the noise.Moreover,the power of the interfered samples in the time-domain is weakened.

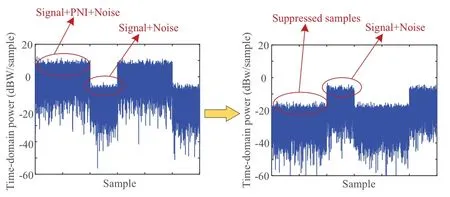
Figure 3.The effect of the adaptive time-domain IS for the PNI.

By substituting(2),(6),(7),(11)and(12)into(10),the distribution of the received symbol-level samples after the adaptive time-domain IS can be obtained as

where the cross-correlation operation characterizes the degree of correlation between the local symbol-level samplesand the received symbol-level samples after the adaptive timedomain IS,which can be used to construct the decision metric of the proposed FHPC-based algorithm.

By substituting(1),(13)and(14)into(15),the distribution ofcan be obtained as

Compared to the decision metric which uses the hard decision of each single pulse [14],the decision metric of the proposed FHPC-based algorithm usesas the combining coeffciients to accomplish the non-c oherent combining,which can enhance the acquisition performance of the synchronization acquisition under the PNI.Therefore,the decision metric and the decision rule of the proposed FHPC-based algorithm are defnied as

whereudenotes the decision metric.L=32 denotes the number of the coarse synchronization pulses in Figure 1.TPNIdenotes the acquisition decision threshold under the PNI.

The analysis shows that theLvariablesare statistically independently distributed.Therefore,uobeys a chi-square distribution with 2Ldegrees of freedom,i.e.,u～X2(2L),and the conditional probability density function(PDF)ofucan be obtained as

From(18),a false alarm event can be defnied as the situation where the decision metricuis greater than the acquisition decision thresholdTPNIwhenH=H0.Therefore,the false alarm probability is obtained as

whereZ(x,α) denotes the incomplete Gamma function which is formulated by

The CFAR criterion in the synchronization acquisition is an important requirement,i.e.,the false alarm probability is constant for different noise and interference intensities.Therefore,the adaptive acquisition decision threshold of the proposed FHPC-based algorithm under the PNI is obtained as

whereZ-1(·,·)denotes the inverse function of the incomplete Gamma functionZ(·,·).

From(18),an acquisition event can be defnied as the situation where the decision metricuis greater than the acquisition decision thresholdTPNIwhenH=H1.Therefore,the acquisition probability under the PNI is obtained as

whereQm(α,β) denotes the generalized Marcum Qfunction which can be formulated by

(23) characterizes the relationship between the acquisition probability of the proposed FHPC-based algorithm and the signal to interference plus noise ratio(SINR)of the PNI with a preset false alarm probabilityPF.

The detailed steps of the FHPC-based algorithm under the PNI is presented in Algorithm 1,which is a summary of this subsection.

3.3 The Proposed Algorithm Under the NBNI

As shown in(3)and(4),the NBNI can be regarded as the Gaussian noise whose bandwidth is less than that of the DS spread spectrum signal.For the frequencydomain interference,the adaptive IS module of the proposed FHPC-based algorithm adopts the 1/2 overlapping windowing processing,which is shown in Figure 4 [19].The input symbol-level samples are grouped,and then be divided into two branches for frequency-domain IS.Note that the windowing in the traditional method,e.g.,using the Hanning window or the Kaiser window,can effectively reduce the spectrum leakage in the frequency-domain but causes the signal distortion,whereas the 1/2 overlapping windowing can be realized through the delay operation of the two branches to reduce the spectrum leakage while reducing the signal distortion.

As shown in the figure,the inputdenotes the symbol-level samples of thel’th pulse which are extracted fromy(fi)according to the frequency hopping pattern in Figure 1.Thenare grouped as

The symbol-level samples of the two branches after the delay,windowing,discrete Fourier transform(DFT),frequency-domain IS,and inverse discrete Fourier transform(IDFT)can be expressed as

where diag denotes the diagonal matrix operator.Similar to(12),the IS coefficients are designed as

where the split operation follows the inverse operation in(25),anddenotes the matrix formed by combining the row vectors of

From(26)-(29),the effect of the adaptive frequencydomain IS for the NBNI is shown in Figure 5.The interfered frequency-domain samples are multiplied by the suppression coefficients,i.e.,hence the deterioration of the NBNI is weakened.

By substituting (3),(4),(6),(7),(27) and (28)into(29),the distribution of the received symbol-level samples after the adaptive frequency-domain IS can be obtained as

whereHlandΦldenote the corresponding initial phase diagonal matrix and channel diagonal matrix from(6)and(7),respectively.

Similar to (15),the normalized cross-correlation value is defnied as

where the cross-correlation operation characterizes the degree of correlation between the local symbol-level samplesand the received symbol-level samples after the adaptive frequency-domain IS,which can be used to construct the decision metric of the proposed FHPC-based algorithm.

By substituting(1),(30)and(31)into(32),the distribution ofcan be obtained as

Similar to(18),the decision metricuand the decision rule of the proposed FHPC-based algorithm are defnied as

whereudenotes the decision metric.TNBNIdenotes the acquisition decision threshold under the NBNI.

Similar to (22),the acquisition decision threshold under the NBNI is obtained as

Compared to (22),the acquisition decision threshold under the NBNI is the same as that under the PNI,henceTh=Z-1(PF,L) is regarded as the adaptive acquisition decision threshold of the proposed FHPCbased algorithm.

Similar to(23),the acquisition probability under the NBNI is obtained as

The detailed steps of the FHPC-based algorithm under the NBNI is presented in Algorithm 2,which is a summary of this subsection.

IV.NUMERICAL RESULTS

In this section,numerical results are presented to verify the anti-interference and anti-noise performances of the proposed FHPC-based algorithm.

4.1 Simulation Parameters

In our simulations,the channel type is the single-path Rician channel,and the interference type is the PNI or the NBNI.Assuming that the maximum carrier frequency is 1.206 GHz,and the maximum relative motion speedvis 4Mach between the transmitter and the receiver,the maximum Doppler shiftfdcan be obtained asfd=max{f}v/c ≈5467Hz,wherecdenotes the speed of light.Therefore,The simulation parameters are summarized in Table 1.

Table 1.The simulation parameters.

Note that in order to compare with the antiinterference performance of the algorithm in [14],which we call the BD algorithm,the same adaptive IS module in Figure 2 is also added to the BD algorithm for the fair comparison.

4.2 Performances Without Interferences

The anti-noise performances without interferences whenPFis set to different values are shown in Figure 6.Note thatEsdenotes the energy per modulated symbol,andN0denotes the power spectrum density(PSD) of the noise.As shown in the right subgraphs in Figure 6a and 6b,the simulated false alarm probabilities of both two algorithms fluctuate within 10-3orders of magnitude and 10-2orders of magnitude,respectively,which satisfeis the design requirement of the approximately constantPFand proves the effectiveness of the adaptive acquisition decision threshold.Besides,it is fair to compare the acquisition probabilities of the two algorithms at this time.As shown in the left subgraphs in Figure 6a and 6b,as we take the acquisition probability of 98%as the standard,the anti-noise performances of the proposed FHPC-based algorithm are about 1dB better than those of the BD algorithm when the initial frequency offset Δfis in the range of 10k～50kHz.Theoretically,the FHPC-based algorithm employs the noncoherent combining of the pulses to enhance the SNR of the decision metric when compared to the hard decision on each single pulse in the BD algorithm.Therefore,the anti-noise performances of the proposed FHPC-based algorithm in the environments without interferences are better than those of the BD algorithm.

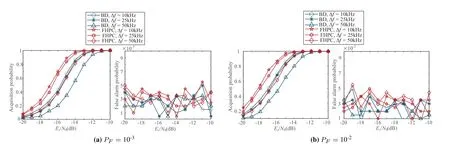
Figure 6.The anti-noise performances without interferences.

4.3 Performances Under the PNI

The anti-interference performances under the PNI whenPFis set to different values are shown in Figure 7.As shown in the right subgraphs in Figure 7a and 7b,the simulated false alarm probabilities of both two algorithms also satisfy the design requirement of the approximately constantPF,and prove the effectiveness of the adaptive acquisition decision threshold,i.e.,(22).As shown in the left subgraphs in Figure 7a and 7b,the anti-interference performances of the proposed FHPC-based algorithm are about 1dB better than those of the BD algorithm.When the interference power of the PNI is large,the adaptive timedomain IS operation,i.e.,(10),reduces the deterioration of the PNI on the received pulses,and the combining coeffciients,i.e.,in (17),enhance the signal-to-interference ratio(SIR)of the decision metric,i.e.,(18),of the proposed FHPC-based algorithm.Therefore,the anti-interference performances of the proposed FHPC-based algorithm under the PNI are more advantageous than those of the BD algorithm.

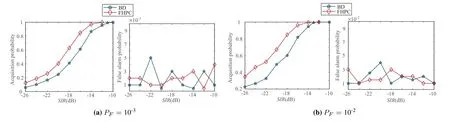
Figure 7.The anti-interference performances under the PNI(Es/N0=-8dB,Δf=10kHz).

The anti-noise performances under the PNI whenPFis set to different values are shown in Figure 8.As shown in the right subgraphs in Figure 8a and 8b,the simulated false alarm probabilities of both two algorithms also prove the effectiveness of the adaptive acquisition decision threshold,i.e.,(22).As shown in the left subgraphs in Figure 8a and 8b,the anti-noise performances of the proposed FHPC-based algorithm are about 1dB better than those of the BD algorithm,this is because the decision metric in (18) of the proposed FHPC-based algorithm utilizes more information from the cross-correlation values when compared to the hard decision in the BD algorithm.Therefore,the anti-noise performances of the proposed FHPCbased algorithm under the PNI are still advantageous.

4.4 Performances Under the NBNI

The anti-interference performances under the NBNI whenPFis set to different values are shown in Figure 9.As shown in the right subgraphs in Figure 9a and 9b,the simulated false alarm probabilities of both two algorithms also satisfy the design requirement of the approximately constantPF,and prove the effectiveness of the adaptive acquisition decision threshold,i.e.,(36).As shown in the left subgraphs in Figure 9a and 9b,the anti-interference performances of the proposed FHPC-based algorithm are about 0.5dB better than those of the BD algorithm.When the interference power of the NBNI is large,the adaptive frequency-domain IS operation,i.e.,(29),reduces the deterioration of the NBNI on the the frequency domain samples,and the combining coeffciients,i.e.,in(34),enhance the SIR of the decision metric,i.e.,(35),of the proposed FHPC-based algorithm.Therefore,the anti-interference performances of the proposed FHPC-based algorithm under the NBNI are more advantageous than those of the BD algorithm.

Figure 9.The anti-interference performances under the NBNI(Es/N0=-8dB,Δf=10kHz).

The anti-noise performances under the NBNI whenPFis set to different values are shown in Figure 10.As shown in the right subgraphs in Figure 10a and 10b,the simulated false alarm probabilities of both two algorithms also prove the effectiveness of the adaptive acquisition decision threshold,i.e.,(36).As shown in the left subgraphs in Figure 10a and 10b,the anti-noise performances of the proposed FHPC-based algorithm are about 1dB better than those of the BD algorithm,this is because the decision metric in (35) of the proposed FHPC-based algorithm utilizes more information from the pulses when compared to the hard decision on each pulse in the BD algorithm.Therefore,the anti-noise performances of the proposed FHPC-based algorithm under the NBNI are still advantageous.

Figure 10.The anti-noise performances under the NBNI(SIR=-14dB,Δf=10kHz).

V.CONCLUSION

In this paper,the FHPC-based synchronization acquisition algorithm for hybrid DS/FH communications has been proposed and this algorithm is composed of an adaptive interference suppression module and an adaptive combining decision module,which can complete the adaptive synchronization acquisition in the environments with interferences.Theoretical and numerical results demonstrate that the FHPC-based algorithm can reduce the deterioration of the PNI or the NBNI on the received pulses and can enhance the SINR of the decision metric,hence the FHPCbased algorithm improves the anti-interference and anti-noise performances under the PNI or the NBNI.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China(NSFC)under Grants 62131005,62071096,in part by the Fundamental Research Funds for the Central Universities under Grant 2242022k60006,in part by the National NSFC under Grant U19B2014,and in part by the Natural Science Foundation of Sichuan under Grant 2022NSFSC0495.