Channel-Feedback-Free Transmission for Downlink FD-RAN:A Radio Map Based Complex-Valued Precoding Network Approach

Zhao Jiwei ,Chen Jiacheng ,Sun Zeyu ,Shi Yuhang ,Zhou Haibo,* ,Xuemin(Sherman)Shen

1 School of Electronic Science and Engineering,Nanjing University,Nanjing 210023,China

2 College of Information Science and Electronic Engineering,Zhejiang University,Hangzhou 310058,China

3 Department of Mathematics and Theories,Peng Cheng Laboratory,Shenzhen 518000,China

4 Department of Electrical and Computer Engineering,University of Waterloo,Waterloo,Ontario,N2L 3G1,Canada

Abstract: As the demand for high-quality services proliferates,an innovative network architecture,the fully-decoupled RAN (FD-RAN),has emerged for more flexible spectrum resource utilization and lower network costs.However,with the decoupling of uplink base stations and downlink base stations in FDRAN,the traditional transmission mechanism,which relies on real-time channel feedback,is not suitable as the receiver is not able to feedback accurate and timely channel state information to the transmitter.This paper proposes a novel transmission scheme without relying on physical layer channel feedback.Specifcially,we design a radio map based complex-valued precoding network (RMCPNet) model,which outputs the base station precoding based on user location.RMCPNet comprises multiple subnets,with each subnet responsible for extracting unique modal features from diverse input modalities.Furthermore,the multimodal embeddings derived from these distinct subnets are integrated within the information fusion layer,culminating in a unifeid representation.We also develop a specifci RMCPNet training algorithm that employs the negative spectral effciiency as the loss function.We evaluate the performance of the proposed scheme on the public DeepMIMO dataset and show that RMCPNet can achieve 16%and 76%performance improvements over the conventional real-valued neural network and statistical codebook approach,respectively.

Keywords: beamforming;complex neural networks;deep learning;FD-RAN

I.INTRODUCTION

With the explosive growth of mobile communication demand,multi-antenna systems have been widely deployed to provide spectrum-effciient transmission and meet more stringent service requirements[1-7].Currently,the multi-antenna transmission in 5G is based on codebook and requires feedback to let the transmitter know the channel information in order to precode original signals loaded into different antennas [8].However,as the number of antennas increases,more pilots are needed to obtain the channel between users and base stations,and the feedback of the channel has become a signifciant obstacle to achieving higher spectral effciiency of wireless communication[9-12].Furthermore,considering the channel variation in the practical environment,the feedback information used by base stations for precoding may become outdated and thus invalid [13,14].This leads to a signifciant decline in the performance of the multi-antenna transmission,especially when the channel changes fast,such as in mobile scenarios.Moreover,in fully decoupled radio access networks (FD-RAN),where the uplink base stations (UBSs) and downlink base stations (DBSs) are physically decoupled,the transmission resources for feedback will be more scarce because users in a wide area share the same control base station [15].Hence,exploring a new transmission mechanism for massive MIMO becomes an indispensable yet challenging task.

Many recent works have attempted to solve the challenges faced by real-time feedback based communications.With the development of autoencoder,channel state information(CSI)compression based on deep learning has attracted wide attention from researchers[9,16,17].Specifcially,CSI is compressed from different frequency domain and spatial domain into bit streams to reduce the amount of feedback data [18-21].Literature [18] proposes a fully convolutional neural network that incorporates quantization and entropy coding blocks into its design,improving CSI recovery accuracy.Yinet al.propose a CSI compression and feedback network based on a self-information model [19].Literature [20] proposes a network with self-attention and dense refnie mechanisms.These neural network-based methods for CSI compression improve feedback accuracy and are suitable for different channel compression ratios.However,these works are still based on real-time feedback of channels.They cannot solve the challenge of outdated channel feedback caused by delay and channel variations.

Another effective approach to deal with outdated channel feedback is to use statistical information of channels for transmission [22-29].Literature [22]considers the closed-form upper bound of channel capacity when only statistical channel state information is available at the transmitter.[23] derives a closedform expression for optimal linear precoding.[25]proposes a downlink transmission method based on channel statistical information that considers physical layer security.Muhammadet al.design a learning framework that is an integration of a convolutional neural network and a long short term with memory network[29].

Shiet al.exploit the structural characteristics for the optimal precoding and propose a deep neural network(DNN)based robust precoding method that learns directly from CSI statistical knowledge [26].The online computational complexity of the precoder is substantially reduced compared with the existing iterative algorithm while maintaining nearly the same performance.

Location-based precoding techniques have attracted considerable interest from academia owing to the relatively stable statistical characteristics of the channel at the user’s location [30-36].By integrating the navigation information and wireless channel information,Wang et al.enhance the performance of cellularenabled UAV communications by predicting the angle of arrival [33].In literature [36],a historical channels based convolutional long short-term memory network is proposed for predicting beamforming.In addition,literature[30,34]exploits deep learning models to predict the beamforming vectors and further support highly mobile users.Most deep learning based communication techniques are based on real-valued neural networks(RVNN),which may lead to performance degradation for ignoring the correlation between In-Phase/Quardrature(IQ)components[37].

In recent years,complex-valued neural networks(CVNN)[37-39]have been applied to different communication scenarios due to their superior performance and ability to directly process complex-valued data,including channel prediction [40],modulation classifciation [41],OFDM receiver [42],etc.Literature[42,43]validate that a deep complex-valued neural network has advantages on complex baseband signal processing.A lightweight CLNet with a complexvalued input layer effectively extracts complex-valued features of input[44].Nevertheless,to the best of our knowledge,CVNN has not been employed for predicting the precoding for multi-antenna transmission.

The precoding vector/matrix is complex-valued,and the channel statistics are also typically complex.Considering the advantages of complex neural networks in handling complex data,as well as the current dilemma of channel feedback for massive MIMO in 5G[9,43],we propose a radio map based complex-valued precoding network (RMCPNet) model,which predicts the precoding for transmitting to the user with multiple antennas based on user positions and corresponding complex channel statistics.The contributions of this paper are summarized as follows:

• We propose a downlink channel-feedback-free transmission approach in the FD-RAN based on user positions and historical channel statistics in the specifeid spatial domain.The new transmission approach will largely reduce the usage of precious spectrum resources required for channel estimation and feedback.

• Considering that wireless signal processing is usually realized in the complex domain,we propose a complex-valued precoding network based on the radio map.The network can achieve fusion perception of multi-modal information,including user position,transmission/reception correlation matrix,etc.,thus improving achievable spectral effciiency.

• Based on publicly available ray tracing data[45],we conduct extensive performance evaluation and provide result analysis for the proposed method.Simulation results show that our proposed method can outperform real-valued neural networks and the statistical codebook scheme.

The rest of the paper is organized as follows.Section II presents the system model and problem formulation.Then,we elaborate on the proposed RMCPNet architecture and corresponding training algorithm in Section II.In Section IV,the simulation scenarios,settings,as well as corresponding simulation results are explained in detail.Finally,we conclude the paper and point out some potential research directions in Section V.

II.SYSTEM MODEL AND PROBLEM FORMULATION

Figure 1 illustrates the downlink transmission in FDRAN without real-time physical layer feedback.We assume that the edge cloud has stored the spatial domain statistical information about the channel,which is periodically updated to adapt to changes in the environment.The edge cloud deploys RMCPNet for user downlink precoding.In this paper,we focus on the single-user case of multi-antenna transmission.First,a user will upload position information to the edge cloud via the control base station.Note that the position feedback is less sensitive than the channel feedback.Then,the edge cloud inputs the user’s position information and corresponding channel statistical information stored on the cloud server into RMCPNet to generate precoding and deliver to the serving data base station.Last,the DBS will perform beamforming to serve the user.

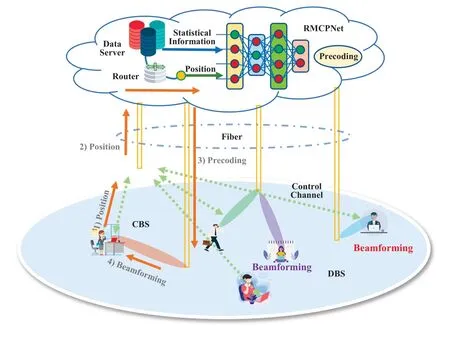
Figure 1.The proposed channel-feedback-free transmission in the downlink FD-RAN.

According to[45]the channel between base stationband userkon carrieruis expressed by:

whereais the array response vector of the BS.Since we only consider a single base station serving a single user within a subband,for simplicity of analysis,we denote the channel of userkwith

whereGk ∈CNk×Mrepresents the beam domain channel matrix,Nkis the number of antennas for userk,andMdenotes the number of antennas for DBS.As shown in Eq.(2),Vis independent of the user’s position and only depends on the geometry of the base station antenna array.When the base station employs a uniform linear array (ULA) with half-wavelength antenna spacing,we haveIn this case,Vcan be approximated by a discrete Fourier transform (DFT) matrix.We assume that the signal transmitted by userkisqk ∈RM,which satisfeis

For convenience of notation and to simplify the analysis,we will omit the subscript for userkin the remainder.We assume that the precoding vector for userkat the base station isw,and the signal sent by the base station is

wherenrepresents the circularly symmetric complex Gaussian noise with zero mean and covariancei.e.,

Based on the channel capacity of MIMO channels,we can obtain the ergodic rate:

Our problem is to design a precoding strategy for massive MIMO downlink transmission that maximizes spectral effciiency

It implies that the downlink transmission signal should be oriented along the base station-related matrix’s eigenvectors to achieve the system’s maximum spectral effciiency.Hence,beam domain transmission facilitates spectral effciiency optimization in downlink massive MIMO.Consequently,problemF1can be reformulated asF2

ForF2,it is challenging to use the Monte Carlo method to solve.Based on the property of the det matrix,we obtain the following equation:

Applying Jensen’s inequality,we can acquire the following:

whereλiis power,and E{GHG}is the statistical information of the channel.Hence,the base station’s precoding can be derived from the channel’s statistical information.

III.RADIO MAP BASED CHANNELFEEDBACK-FREE TRANSMISSION

In the following,we will further derive how to achieve feedback-free transmission.

3.1 Radio Map

FromF3,we can acquire that the precodingwcan be derived from the statistical information of the channel E{GHG}.Given thatH=UGVH,we defnie the statistical information of the channel asRt:

We can analogously defnie the statistical informationRr:

Based on reference [22],we defnie the statistical power information

that characterizes the channel.

3.1.1 The Concept of Radio Map

We divide the area of interestPinto different small regionsp ∈P.In this paper,we refer to map information asS,and the statistical information is denoted as

which can completely capture the channel’s fading and correlation information.In the following,the radio map is defnied as the mapping from each spatial regionpto the corresponding channel statistical information

3.1.2 The Construction of Radio Map

According to the defniition of radio map(17),we assumed that each user would collect channel statistics for their position.After long-term channel statistics,the user will periodically upload the positionpand corresponding statistical informationS(p)to the edge cloud.Through broad statistics for all users located at the spatial domainP,the edge cloud will possess complete radio maps for the area,i.e.,S(p),p ∈P.During the service period,each user uploads the positionp,and the edge cloud determines the precoding vectorwbased on{Rt(p),Rr(p),Rp(p)}.

3.2 Radio Map Based Downlink Transmission

In the following,we defnie the functionw=f(p,S(p)) as the mapping from the channel statistical information to the corresponding precoding,and our aim is to fnid such a function.In this paper,we will reformulate our objective as to how to leverage the channel’s statistical informationS(p)to obtain the user’s precoding

The functionfcannot be derived by theoretical calculation.According to reference[36],such a functionfθcan always be approximated by a neural network when the depth and width of the network reach a certain level.Therefore,in this paper,we adopt a datadriven approach to solve the precoding problem.Assuming thatθis the network parameter,then we have

which represents the precoding unit vector when the user is at positionp.

Consequently,our ultimate goal is to obtain an optimal model parameterθthat maximizes the user’s throughput:

whereρdenotes the SINR at the receiver.The model parameterθultimately determines the network performance.

3.3 Complex Neural Networks

In complex-domain signal processing,the convolution of signals in the time domain is precisely equivalent to the multiplication of signals in the complex domain.As both the precoding and the channel of wireless communication are complex,the complex-domain operation is more appropriate for signal processing,as it can better capture the relationship between the real and imaginary components of the channel.

3.3.1 Complex Layer

For a complex operationf,a complex-valued neuron performs the following processing on a complex input[37]

whereψRandψIindicate the neuron’s real and imaginary processing channels,respectively.For instance,the complex convolution operation is realized as illustrated in Figure 2,whereMIandMRdenote the imaginary and real feature maps,andKIandKRdenote the imaginary and real convolution kernels [37].MIKIsignifeis the real-valued convolution outcome between the imaginary convolution kernelKIand the imaginary feature mapMI.

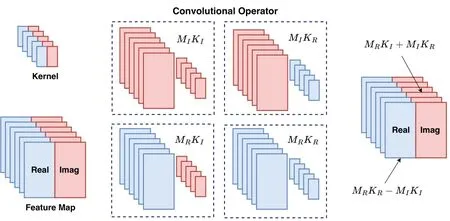
Figure 2.Illustration of the complex convolution operator.

3.3.2 Activation Unit

We employ Complex PReLU (CPReLU) as the complex activation function,which applies separate PRe-LUs to both the real and imaginary parts of a neuron,i.e.

CPReLU satisfeis the Cauchy-Riemann equations when both the real and imaginary parts are simultaneously either strictly positive or strictly negative.

3.3.3 Complex Differentiation and Chain Rules

When training neural networks,the backpropagation algorithm requires the calculation of gradients to update the weight parameters.However,the incorporation of complex values poses challenges for computing gradients of activation functions and loss functions during the backpropagation process.SupposeLis a real-valued loss function andzis a complex variable,wherez=x+iyandx,y ∈R.In this case,we have the following equations:

Then,given another complex variablet=r+iswherezcould be expressed in terms oftandr,s ∈R,we would have the complex chain rules

as described in the literature[37].

3.4 RMCPNet for Downlink Transmission

In Figure 3,we present the overall architecture of RMCPNet.The network comprises four stacked layers:the input layer,the feature extraction layer stack,the feature fusion layer stack,and the output layer.

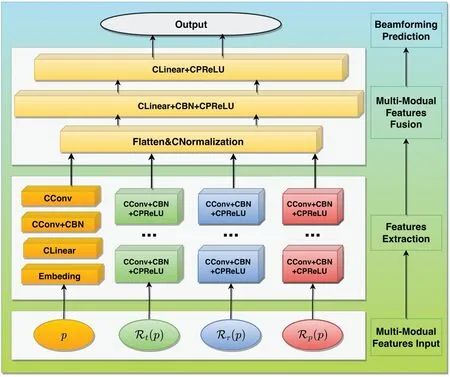
Figure 3.The framework of RMCPNet.

Considering the heterogeneity of different information,we partition the informationS(p) into four parallel subnetworks to input different position information and statistical information to the network,which achieves the feature extraction of heterogeneous information.For the position encoding subnetwork,we frist convert the input two-dimensional positionpinto a complex number,and then map it to a higher-dimensional feature through a fully connected layer.The high-dimensional feature then undergoes a convolution layer,complex batch normalization,and two successive CConv layers to obtain the two-dimensional encoding ofp.The transmission correlation matrixRt(p),the reception correlation matrixRr(p),and the channel fading matrixRp(p) are processed by three successive CConv,CBN,and CPReLU layers,respectively,to obtain the channel transmission coherence encoding,reception coherence encoding and channel fading encoding.In the feature fusion layer,we use Flatten and CBN to concatenate and fuse the features obtained by the four subnetworks.After multi-modal information fusion,we use CLinear CBN and CPReLU to process the fused features.The network fnially produces the precoding outputfθ(p,S(p))through CPReLU.

In this paper,our objective is to maximize the spectral effciiency,which is equivalent to minimizing the negative spectral effciiency.Since we encounter diff-i culty obtaining the optimal precodingwby the Monte Carlo method,we can acquire the overall spectral effciiency when applying the precodingwθ(p)by equation(17).In the following,we denote a sample as

Then,a batch of samples can be denoted as

whereBsis batch size.Therefore,the loss function can be calculated as

When a batch of training dataXbis fed into the RMCPNet,we can obtain the average throughput lossL(Xb) at this point.When training the network,the proposed training algorithm 1 is goal-oriented and directly trains the network,which updates the network parameters in the direction of maximizingL(Xb).In this algorithm,we constrain the maximum epochImax,and add an algorithm convergence condition to terminate the training early(whether theL(Xb)obtained by successiveNterepochs decreases).The learning rateγis executed by exponential decayγ=0.9*γby detecting whether theL(X)obtained by successiveNlrepochs decreases.

IV.SIMULATION RESULTS

In this section,we explain the detailed simulation setup and show the comparison with several benchmark precoding methods.

4.1 Simulation Scenario and Data Collection

As illustrated in Figure 4,we consider the simulation scenario based on the DeepMIMO outdoor dynamic scenario‘O2 Dynamic’[45]to study the performance of our proposed method.The major simulation hyperparameters are summarized in Table 1.There are two DBSs located in the area,and users are distributed in the green rectangular areaPin which we sample up to 100,000 candidate positions to construct the radio map.

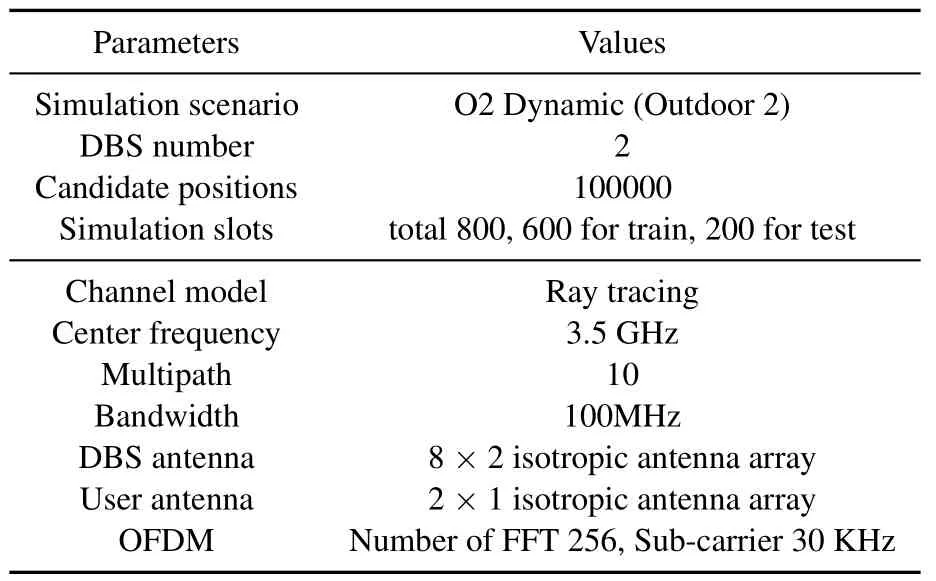
Table 1.Simulation hyperparameters.

Figure 4.The simulation scenario.

We simulate 800 time slots to collect channel data.Specifcially,the frist 600 slots are used to generate the radio mapS(p),p ∈ Pand train the RMCPNetfθ(p,S(p)),while the remaining 200 slots serve to verify the effectiveness of the proposed method.For each positionp ∈P,we collect corresponding channelsH,and compute the radio statistical featureS(p),which constitutes a training samplexi={p,S(p),H}.Then,we can build the radio mapSand acquire the dataset.

In this paper,we employ four benchmark methods to verify the effciacy of our proposed algorithm.

• No Precoding (NoP).No precoding is applied,and all antennas transmit simultaneously.

• Statistical Codebook (SCB).A codebook is used to select precoding.The precoding that has been used most frequently in the training slots at positionpis adopted as the precoding for the user at that position for the test.

• Neural Networks(NN).We train real-valued neural networks with the same structure as complex neural networks to perform precoding among multiple antennas.

• Singular value decomposition (SVD).We calculate the precoding with SVD,which is the theoretically optimal method.

In Table 2,we describe the detailed structure of the RMCPNet.Next,we will simulate and validate the performance of the proposed algorithm from different perspectives.

Table 2.RMCPNet structure description.

4.2 Channel Distribution of Angular Domain

Calculating the power azimuth spectrum(PAS)of the channel,we observed a strong correlation between the user’s location/angle and the direction of maximum spectral energy density.Figure 5 delineates the PAS for precoding utilizing both a random sample and RMCPNet.We observe that the precoding obtained by RMCPNet can point more precisely to the angle and energy peaks of the channel,resulting in a higher received channel power as compared to the SCB method.This enhancement can be ascribed to the superior accuracy in beamforming directions afforded by our methodology.Moreover,since RMCPNet outputs the precoding vector,it can generate multiple beam directions in the spatial domain to accommodate the energy distribution of the channel smallscale fading in different directions.Consequently,our proposed strategy demonstrates superior performance and robustness in the face of channel variations.

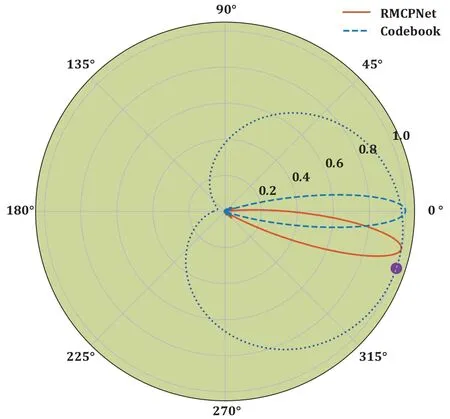
Figure 5.The PAS for a sample of channel,RMCPNet precoding,and SCB precoding.

4.3 Spectral Efficiency

Figure 6 shows that the proposed RMCPNet method signifciantly outperforms the SCB and NN methods.Specifcially,RMCPNet has very few users with spectral effciiency below 7 bit/Hz/s,while many users of the SCB method have spectral effciiency below 5 bit/Hz/s.Moreover,we fnid that the SCB method,which obtains the optimal precoding based on historical statistics,is challenging to work in the complex time-varying electromagnetic environment with multipath.In addition,compared to the NN method,RMCPNet can effectively reduce the probability of choosing suboptimal precoding.However,the major drawback of RMCPNet is that it cannot achieve a higher spectral effciiency level (above 15bit/s/Hz) compared with the optimal precoding scheme based on SVD.This is because the current RMCPNet does not introduce a multi-stream mechanism that can achieve spatial multiplexing.

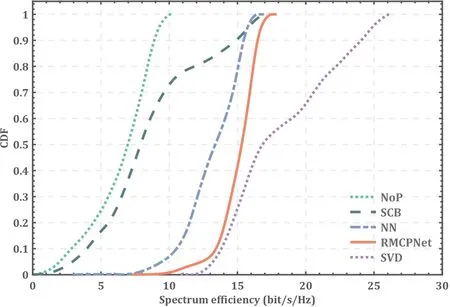
Figure 6.The CDF of the average spectral efficiency for different algorithms.

Figure 7 compares the average spectral eff-i ciency achieved by different algorithms.The proposed scheme is far superior to the statistical precoding method,boasting a performance enhancement of 76%.Compared with the NN approach,we still have a 16%performance improvement,which indicates that our network architecture design is more reliable.Compared with the optimal precoding based on SVD,RMCPNet can still achieve 82.4% of the optimal performance.This discrepancy presents an opportunity for future refniement,specifcially through the adoption of a multi-stream technique.

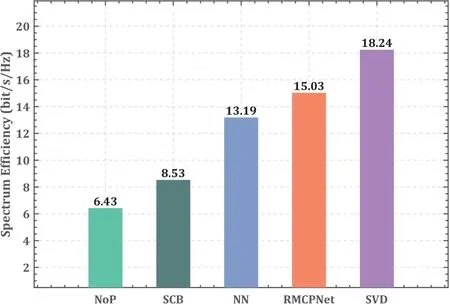
Figure 7.The average spectral efficiency of different algorithms.

In Figure 8,the transmission power of the base station is adjusted from-30dBm to 20dBm.It is observed that RMCPNet still achieves the best transmission performance compared to other single-stream transmission schemes,which demonstrates that our proposed algorithm is robust and can achieve good performance for different transmission powers.

Figure 8.The average spectral efficiency of different algorithms varies with the transmission power.

According to the phenomena illustrated in Figure 6 and Figure 7,insights reveals that the observed performance enhancement stems chiefly from three factors:the radio map’s adept characterization of the channel’s statistical properties,the proposed multi-modal information fusion architecture’s enhanced capability to distill the channel’s intrinsic properties,and the complex neural processing unit’s superior effciiency in handling complex channel values.

4.4 SNR at Different Positions

Figure 9 compares the signal-to-noise ratio (SNR)achieved by RMCPNet and the SCB method across various locations.Our method outperforms the SCB scheme,i.e.,demonstrating superior signal coverage.Notably,the statistical codebook scheme generates more distinct beams in proximity to the base station,where SNR levels are elevated.Conversely,in regions distant from the base station,characterized by diminished SNR,there is a noticeable variability in the positions with high and low SNR within these areas.This variability may stem from the augmented unpredictability of channel energy distribution under low SNR conditions,leading to erratic codebook selection and suboptimal performance.In comparison,approach consistently maintains elevated SNR levels across the entire spatial domain,showcasing its robustness and effectiveness.

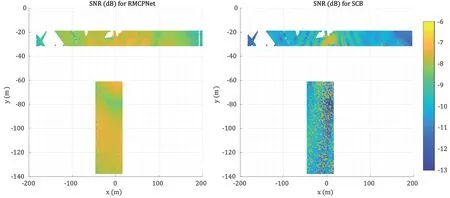
Figure 9.SNR at different positions for RMCPNet and SCB,respectively. Note that the positions are left blank if there is no data available.

V.CONCLUSION

In this paper,we have proposed a transmission mechanism for downlink transmission in FD-RAN without relying on physical layer channel feedback.Furthermore,We have designed a complex-valued precoding network called RMCPNet based on the radio map.To leverage multimodal input information,including user location,channel transmit/recieve correlation matrix,and channel energy matrix,in the RMCPNet,we have further designed several different subnets for multimodal feature extraction.Then,the multimodal encoded features are fused at the feature fusion layer.Considering the computational complexity of obtaining optimal precoding,we have also proposed a specifci network training algorithm with negative spectral effciiency as the loss function.The simulation results of RMCPNet on the public DeepMIMO dataset demonstrate that the proposed RMCPNet delivers signifciantly improved performance compared to traditional neural networks and the statistical precoding method.

In our future work,we plan to further study the impact of feedback delay on wireless transmission and consider precoding in mobile scenarios with the help of predicting user location in real time.We will also implement the feedback-free beamforming method based on the predicted user position and channel statistical information on USRP hardware to verify the feasibility of the proposed scheme in a realistic environment.Furthermore,we will extend the current method to support multi-stream transmission.Additionally,we will study cooperative precoding of multiple base stations.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation Original Exploration Project of China under Grant 62250004,the National Natural Science Foundation of China under Grant 62271244,the Natural Science Fund for Distinguished Young Scholars of Jiangsu Province under Grant BK20220067,and the Natural Sciences and Engineering Research Council of Canada(NSERC).