半地半轨双层立式停车装置框架多目标结构优化

沈仙法，郁锦涛，张 月，陈晓颖

（1.三江学院机械与电气工程学院，江苏 南京 210012；2.南京工业大学机械与动力工程学院，江苏 南京 211816）

1 引言

框架是半地半轨双层立式停车装置重要部件，它是安装框架横移系统和上载车板升降系统的关键承载件。框架结构的设计是否合理直接关系到停车装置的整体稳定性和安全性。框架质量占整个停车装置总质量的49%，因此，为节约材料用量，降低产品生产成本，对其进行结构优化就显得非常重要。

目前，针对立式停车装置相关学者开展了一系列研究。例如文献[1]研究了双车位滚道存放型停车装置如何控制调度及其停车管理系统。文献[2]利用有限元软件对立体车库钢结构骨架的4种工况进行了力学分析和优化设计。文献[3]设计了一种基于组态控制技术的智能停车设备。文献[4]对堆垛式停车库设备的存取车控制系统进行了优化。文献[5]提出了一种立体车库建筑顶部支撑结构隔震优化控制方法。

文献[6]设计了一种三层九车位的小型柱式立体停车库，构建了基于单片机的控制系统。文献[7]提出了一种基于液压传动技术的双层升降横移式立体车库的控制方法。文献[8]设计了一种新型双层立体旋转式无避让停车装置，其空间利用率较普通停车装置提高了2倍，而且上下层同时存取车。文献[9]设计了一种采用跨越梳齿与下行托举复合交换存取的新型立体停车装置，实现了空间的充分利用，提高了停车效率。

综上可知，关于立式停车装置的研究主要集中在大型立体车库的机构原理和控制系统，并取得了一定成果，但是在小型双层立式停车装置的结构优化方面的成果并不多。

故将首先采用UG软件建立半地半轨停车装置框架的三维模型，并根据框架的受力情况和结构特点在ANSYS Workbench软件中进行静力学和模态分析，然后根据分析结果，对框架横梁和立柱进行结构尺寸优化，进而提出框架结构整体优化方案，并进行验证，从而获得满足强度和刚度要求的框架结构参数。

2 停车装置框架静动态分析

2.1 框架三维建模

双层立式停车装置主要包括框架、框架横移系统、上载车板升降系统、下载车板横移系统和电气控制系统[10]。其整机三维结构，如图1所示。

图1 停车装置整机结构图Fig.1 Structure of Parking Device

停车装置框架为全承载式桁架结构，整个框架长5690mm、宽3000mm、高3390mm。框架横梁两端主要安装升降长轴和横移长轴的轴承支座。

根据其在实际工作过程中的受力情况，框架纵梁和横梁均选用了（200×100×3）mm矩形管，框架立柱选用了（200×200×3）mm方管，其三维结构模型，如图2所示。

图2 框架三维结构图Fig.2 3D Structure of Frame

2.2 框架静力学分析

在进行静力学分析之前，需要先将结构进行简化处理，将结构上诸如圆角和小孔之类的非重要特征进行删除，目的是尽量减少ANSYS Workbench 的运算时间[11-12]。然后将停车装置框架的三维模型导入到ANSYS Workbench软件中。

框架采用的型材材料均为Q235A，其力学性能参数，如表1所示。ANSYS Workbench 软件中提供的主要网格划分方法有扫掠法、四面体划分法、自动划分法、多区域法、六面体主体法和笛卡尔法[13-14]。根据框架的几何特点，本次采用了四面体划分法，然后对相关特征面进行映射，再完成细化局部网格，形成高质量的网格模型。最终网格划分完成之后，共生成19795 个单元和36119个节点。

表1 框架材料力学参数Tab.1 Mechanical Parameters of Frame Material

将停车装置框架在工作时静态受力情况作为边界条件输入，在横梁安装轴承座的相应位置施加42361Pa的载荷，同时将立柱底面设置为固定约束，求解完成后获得的框架等效应力、整体变形和安全系数云图，如图3所示。

图3 框架静力学分析结果Fig.3 Static Analysis Results of Frame

从图中可以看出，框架承受的最大应力发生在框架横梁与纵梁的连接交点处，为17.619MPa，远小于其材料的屈服强度值235MPa。框架整体出现的最大变形发生在框架纵梁2的中间位置，为0.4971mm，小于其许用挠度26.45mmm（[ω2]=l2∕200）[15]。框架最小安全系数为14.19，远大于一般安全系数1.5。综上可知，停车装置框架的强度和刚度存在明显冗余现象，因此有必要对停车装置框架进行结构优化。

2.3 框架模态分析

停车装置框架进行模态分析时，其模型建立方法与静力学分析相同，然后在Modal下的Analysis Setting的Option里设定求解算法和模态阶数[16]。本次分析采用的是Direct算法，提取的模态阶数为6，不需要施加外载荷，只需对框架自由度进行约束即可，如表2、图4所示。

表2 框架前6阶固有频率和振幅Tab.2 The First 6 Natural Frequencies and Amplitudes of Frame

图4 框架前6阶模态振型Fig.4 The First 6 Modes of Frame

由框架模态分析可知，框架前6阶固有频率属于低频区域，框架横梁和纵梁的振幅在（1.2054～4.5103）mm之间，其中最大变形出现在框架纵梁2的5阶固频共振时，大小为4.5103mm。如果框架振动变形较大，则会产生较大的交替变化的应力集中和疲劳破坏。通过模态分析获得了框架的模态参数，掌握了框架结构的薄弱部位，为优化设计提供了参考。

3 框架多目标结构优化与分析

3.1 优化模型与流程

多目标优化问题的目标函数一般为两个及以上，其优化数学模型为：

式中：fn(x)—目标函数；

gj(x) ＞0，hi(x) ＞0为约束条件；

j、i—变量个数；

xL，xU—设计变量x的下限和上限。

多目标优化设计流程，如图5所示。

图5 多目标优化流程Fig.5 Multi-Objective Optimization Process

3.2 横梁结构优化

3.2.1 优化数学模型

横梁截面，如图6所示。其结构优化数学模型，如式（2）所示。

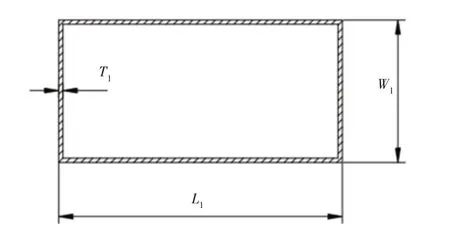
图6 横梁截面图Fig.6 Cross Section of Beam

式中：W1，L1，T1—框架横梁截面的宽度、长度和厚度；

F1(x)=minMmax，Mmax—最大质量；

F2(x)=minσmax，σmax—最大应力；

F3(x)=minTmax，Tmax—最大变形；

F4(x)=maxfmin，fmin—最小安全系数。

3.2.2 试验设计

从响应面优化模块中的DOE模块进入试验设计环节，运用中心复合设计法（Central Composite Designs）确定试验设计点，将横梁截面的宽度P1、长度P2 和厚度P3 作为试验设计因素，将横梁的最大质量P4、最大应力P5、最大变形P6 和最小安全系数P7 作为试验结果，确定各试验因素的变化范围，完成15次中心实验。

从试验结果可知，3个试验因素之间存在相互矛盾现象，如横梁厚度P3减小，虽然会减轻其质量P4，但会增大应力P5和变形P6，反之则相反，因此，必须要对试验数据进行综合处理。根据试验设计点拟合的响应面图，得到框架横梁截面尺寸与最大应力和最大变形之间的变化关系，如图7所示。从图7 可知，框架横梁的最大应力与截面宽度成反比，与截面长度成正比；最大变形与截面宽度和厚度成反比关系。这说明增大横梁截面宽度和厚度可以降低其应力及变形，但会增大质量。

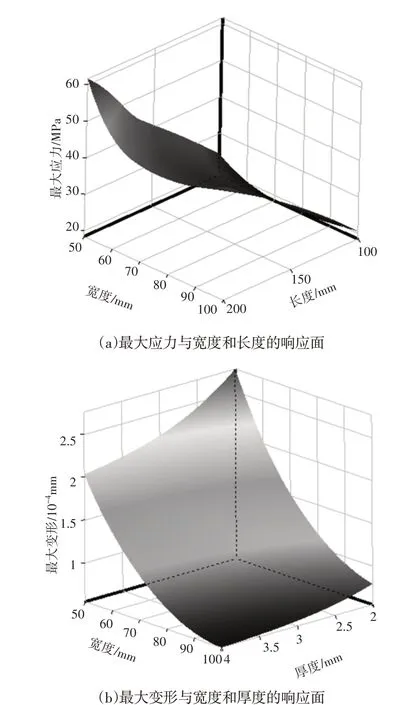
图7 横梁的应力、变形和质量的响应面Fig.7 Response Surface of Stress，Deformation and Mass of Beam

3.2.3 响应面法优化

利用ANSYS Workbench响应面优化模块中的多目标遗传算法（MOGA）对框架横梁截面尺寸进行优化计算［17-18］，设置初始种群大小为600，最大迭代次数为20，收敛准则为70%，获得Pareto最优解集，如图8所示。

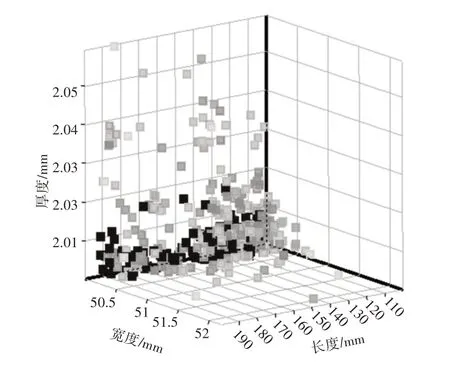
图8 横梁截面尺寸的Pareto最优解集Fig.8 Pareto Optimal Solution Set of Beam Section Size

由最优解集得到优化后的3个候选设计点。根据候选设计点提供的尺寸参数，同时考虑各个输入参数对框架横梁质量、最大应力、最大变形和最小安全系数的灵敏度影响大小以及市场上型材规格尺寸的标准，最终确定横梁截面尺寸为W1=75mm，L1=150mm，T1=3mm。通过计算，单个横梁质量从47.374kg降低为35.206kg，下降了25.68%，达到了减轻材料的目的。

3.3 框架立柱结构优化

3.3.1 优化数学模型

立柱的截面草图，如图9 所示。其结构优化数学模型如式（3）所示。

图9 框架立柱截面图Fig.9 Cross Section of Frame Column

式中：W2，L2，T2—立柱截面的宽度、长度和厚度。

3.3.2 试验设计

同样采用中心复合设计法确定试验设计点，将立柱截面的宽度P1、长度P2和厚度P3作为试验设计因素，将立柱的最大质量P4、最大应力P5、最大变形P6和最小安全系数P7作为试验结果，并完成15次中心实验。由试验结果可知，3个试验因素间一样存在相互矛盾，因此，也需要对试验数据进行综合处理。

根据试验设计点拟合的响应面图，得到框架立柱截面尺寸与应力、变形及质量之间的变化关系，如图10所示。

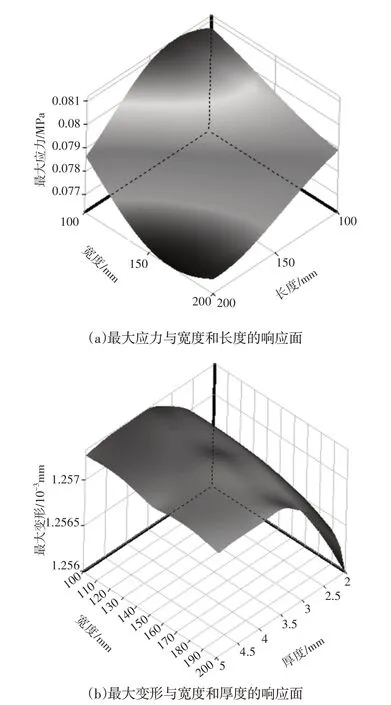
图10 立柱的应力、变形和质量的响应面Fig.10 Response Surface of Stress，Deformation and Mass of Column

从图10可知，框架立柱所受的最大应力与截面宽度和长度成反比关系；最大变形与立柱截面宽度成反比，与截面厚度成正比关系，故优化时在严格控制截面厚度，合理确定截面宽度和长度。

3.3.3 响应面法优化

利用ANSYS Workbench响应面优化模块中的多目标遗传算法对框架立柱截面尺寸进行优化计算，获得其Pareto最优解集，如图11所示。根据最优解集得到立柱截面参数优化后的3个候选设计点。

图11 立柱截面尺寸的Pareto最优解集Fig.11 Pareto Optimal Solution Set of Column Section Size

根据优化后的立柱截面尺寸候选设计点和各输入参数对框架立柱优化目标敏感度大小以及市场型材规格标准，框架立柱的截面尺寸最终选择为W2=150mm，L2=100mm，T2=3mm。经计算，单个立柱质量从63.339kg 降低为39.225kg，下降了38.07%，达到了减材的目的。

3.4 框架整体优化设计方案

综上所述，横梁和立柱的优化结果为框架整体结构优化提供了理论依据，同时依据市场上型材的标准尺寸规格进行了再设计，最终确定框架整体优化方案为：横梁和横梁2截面长度尺寸从200mm改为150mm，宽度尺寸从100mm改为75mm，厚度保持不变，为3mm；立柱截面长度尺寸从200mm改为100mm，宽度尺寸从200mm 改为150mm，厚度保持不变，为3mm；纵梁和纵梁2截面长度尺寸从200mm改为150mm，宽度尺寸也从100mm改为75mm，厚度保持不变，为3mm。

框架整体优化后，总质量由原来的988.731kg 降低为664.645kg，下降了32.78%，因此，可以认为通过优化设计能够节约停车装置的材料用量，从而降低产品成本。

4 优化后的框架静态特性验证

通过对停车装置框架整体结构优化后，由于型材规格的变化，其主要承载部件的接触面积发生了变化，静载荷也随之变化，因此，根据优化结果对停车装置框架重新设计并完成三维建模，再利用ANSYS Workbench 进行了静力学分析，发现框架的最大应力仍然出现在框架立柱与横梁连接交点处，为23.567MPa；整体出现的最大变形也发生在框架横梁的中间位置，为1.0226mm；最小安全系数为10.608。优化前后结果比较，如表3所示。

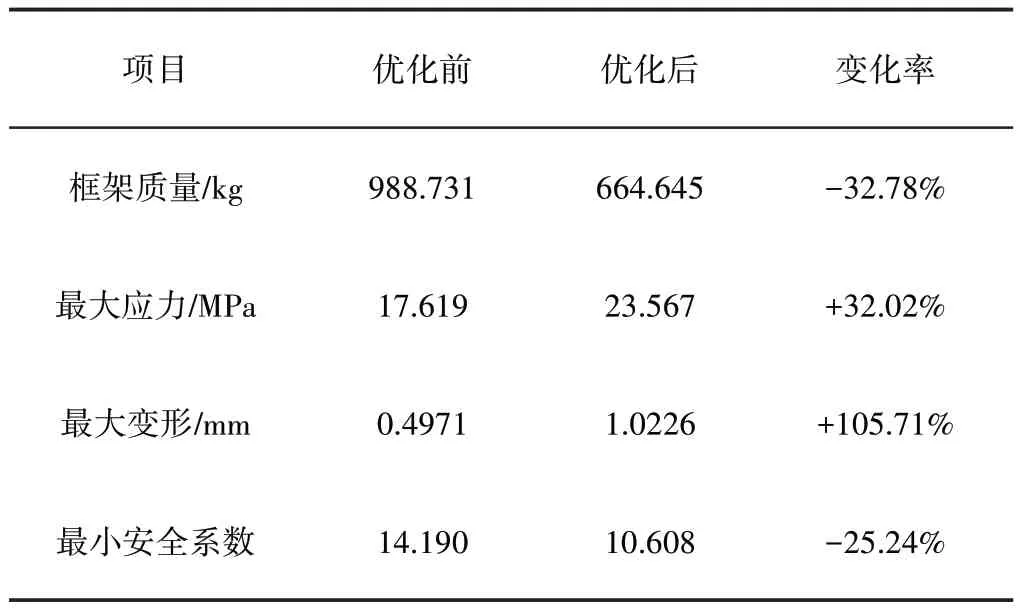
表3 优化前后结果比较Tab.3 Comparison of Results Before and After Optimization

由表3分析可知，优化后，停车装置框架的最大应力虽然增加了32.02%，但是仍小于其屈服强度值235MPa；最大变形增大105.71%，但也小于其许用挠度26.45mmm；最小安全系数减小了25.24%，但是仍大于一般安全系数1.5；而框架整体质量下降了32.78%。因此可以认为，优化后的框架结构仍满足其强度、变形和安全系数的要求。

5 结论

（1）采用UG软件建立半地半轨双层立式停车装置框架的三维模型，再导入ANSYS Workbench 软件中进行静力学和模态分析，得到框架的等效应力、总体变形、安全系数云图和前6阶固有振型与频率，找到停车装置框架结构的冗余和薄弱部位。利用响应面优化模块中的多目标遗传算法对框架横梁和立柱截面尺寸进行优化，由此得到横梁和立柱截面参数的Pareto最优解集和候选设计点，并提出框架整体优化设计方案，最后通过对优化后的框架结构再次进行静力学分析，证明了其强度、变形和安全系数均满足安全要求。

（2）通过对半地半轨双层立式停车装置框架的结构优化，框架总质量由原来的988.731kg降低为664.645kg，降幅达32.78%，从而节约了原材料，降低了产品成本，达到了优化设计目标。优化设计方案为双层立式停车装置框架的结构设计提供了一定的技术指导作用。