纤维预制体渗透率测量技术研究进展*

刘 晓，余映红，崔曦月，卿新林，王奕首

（1. 武汉理工大学信息工程学院，武汉 430070；2. 厦门大学航空航天学院，厦门 361102）

航空航天、先进轨道交通以及海洋工程装备等关系到国民经济发展与国家战略安全，重大装备和工程结构正朝着大型化与智能化方向发展，对材料性能提出更为严苛的要求，不仅要求其具有更高的强度和刚度以减轻结构重量，还要求材料在特殊服役条件下具有优异性能。先进复合材料结构比强度和比刚度高、材料力学性能可设计，具有整体成型等优点，在航空航天、交通运输等领域的大型工程结构中得到越来越广泛的应用，成为大型工程结构减重、提高效能及降低运营成本的有效途径[1–2]。碳纤维增强树脂基复合材料结构的优异性能不但可以帮助航空航天领域实现结构减重、提高飞行器结构使用寿命、降低维护成本的目的，同时还为增加舱内压力和空气湿度，改善舱内环境设计提供了可能[3–4]。随着复合材料技术的快速发展，在飞行器结构上的用量大幅提升[5–6]，大飞机复合材料结构用量已经成为其先进性和市场竞争力的重要标志。尽管复合材料构件数量在过去十年中有巨大增长，由于设计、制造成本及检测技术的限制，其应用的增长速度及其所带来的经济效益与复合材料结构所能提供的优越性能还不匹配，如生产过程中产品质量的不确定性和过裕度设计等[7]。问题的根源在于缺乏实时有效的监测手段和准确的物性参数进行数值模拟，难以及时掌握复合材料制造过程内部的工作状态、工艺参数，进而及时进行有效评估并加以反馈控制[8]。

复合材料结构的制造通常包含树脂在纤维预制体的均匀分散、高温高压固化、冷却脱模等步骤。航空航天领域需要的高性能碳纤维复合材料结构通常使用预浸料由热压罐生产，但是热压罐体型巨大、操作复杂且成本高昂，大大限制了复合材料结构的推广与应用。复合材料液体成型 （Liquid composite molding，LCM）是实现复合材料结构大型化和集成化制造的经济型工艺，适用于制造大尺寸的三维复杂结构，具有低成本、大批量生产的潜力，已广泛用于航空航天、海洋工程装备、大型风机叶片等工业领域[9–11]。

在LCM 家族中，有各种不同的工艺变形体，根据压力不同大致分为两类：

（1）对干燥纤维预制体施加真空，相应环境压力 （0.1 MPa）起压实作用；

（2）通过对树脂加压 （10 MPa甚至更高）使其渗透到干纤维中。

其中第一类只需要单面模具来定义其几何形状，如树脂灌注工艺（Resin infusion，RI）；第二类通常需要闭合模具对干燥的纤维进行充分而坚实的覆盖，以承受渗透压力，最具代表性的是树脂传递模塑成型工艺 （Resin transfer moulding，RTM）。如果在纤维浸渍阶段将空气封存在纤维预制体中，会导致组件中较高的空隙含量而使得成品性能下降，因此在渗透之前，可以通过对封闭的系统施加真空以排除预制体中的空气，这种配置通常称为真空辅助工艺（Vacuum assisted），相应产生工艺变种VARI 和VARTM。

在LCM 工艺树脂灌注阶段，黏性树脂在压力梯度下进入纤维预制体，并逐渐填充纤维丝之间、纤维束之间以及模具和真空袋，封闭系统内的所有空间[12]。树脂灌注过程涉及注气口、排气口、树脂黏度、温度、流动前沿和纤维预制体孔隙率、渗透率等诸多因素，如果工艺参数的取值或组合不合理，会导致复合材料成品中产生干斑或富脂区等缺陷，严重削弱其成品性能[13–15]。复合材料制造工艺离散性大，工艺参数取值问题很难及时纠正[16]，采取反复试验或试错的方法来确定合适的工艺参数又非常低效，因此常用数值模拟分析树脂流动和评估注射前的工艺设计，以确保干燥纤维预制体的完全饱和。基于达西定律的数值模拟预测的准确性依赖于输入参数的准确性，特别是纤维预制体的渗透率，有关其试验测量技术一直是近十年的研究热点，每年相关的出版物均超过150 篇[17]。即使国际上有一些渗透率相关的基准测试，其测试标准一直没有得到建立。由于渗透率根据树脂流动的方向显著不同，呈现高度各向异性，而且面外测量技术难度更高；此外，渗透率的测量与织物结构、试验方法、测试流体类型、流体注入条件、流动前沿传感技术、人为因素等密切相关，纤维制造商必须根据每个具体情况确定，无法提供渗透性值。因此，开发能够准确测定纤维预制体渗透率的试验方法，对于提高数值模拟预测的流动前沿精度具有重要价值，是实现大型复合材料结构液体成型制造工艺参数优化和高产能智能制造亟须解决的关键问题。本文聚焦于复合材料液体成型工艺，对纤维预制体渗透率测量技术的相关研究进展进行综述性分析。

1 渗透率张量

液体成型工艺中其树脂流动过程受达西定律控制，主要描述了平均流速v与树脂灌注压力梯度、树脂黏度η和纺织品的渗透率K之间的关系，如式 （1）和 （2）所示。

可以发现，渗透率K衡量了多孔介质的渗透性，而且为了实现对纤维预制体的完全浸润，数值模拟经常被用于分析树脂流动和评估工艺设计，纤维预制体的渗透率则是其决定性输入参数。各向异性材料的渗透率通常与方向有关，对于三维流动用二阶张量来描述。考虑到织物对称条件，张量可以对角化，同时假设面内和面外流动之间互相独立，仅剩余4 个独立变量就可以描述纤维结构中任何方向的流动，如图1 所示[18]。（1）面内渗透率最大值K1，在纤维预制体平面内沿纤维方向； （2）面内渗透率最小值K2，在纤维预制体平面方向且垂直于K1； （3）面内渗透率最大值K1的旋转角度β，相对于材料的生产角度； （4）面外渗透率K3，垂直于K1和K2。

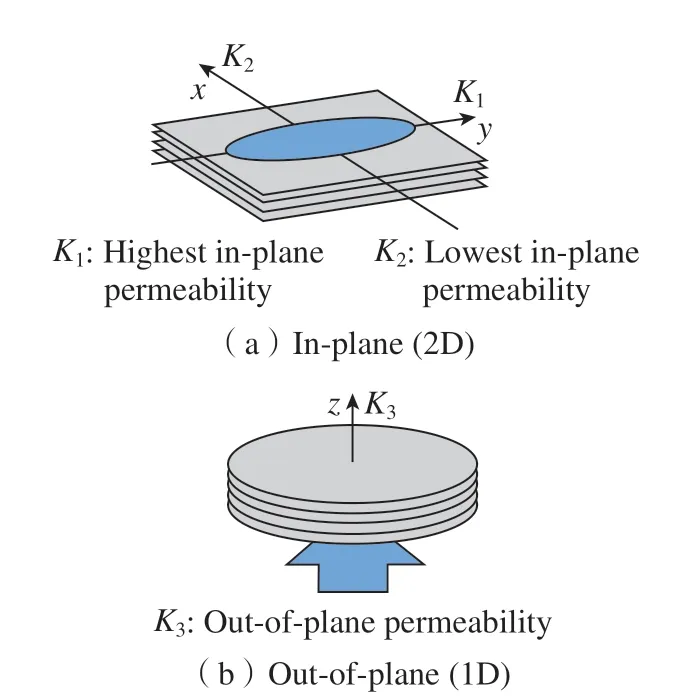
图1 纤维预制体的主渗透率[18]Fig.1 Main permeability of fiber reinforcement[18]

相关研究表明，可以使用Kozeny-Carman 模型进行经验拟合建立渗透率与孔隙率的关系[19]。该模型通过将介质作为任意横截面上的平行流道排列来推导，因此主要用于估算各向同性多孔介质的渗透率K。

式中，ε是纤维预制体孔隙率；df是纤维丝直径；k是Kozeny 常数，通常需要通过试验测量得到。但是对于许多类型的预制体，Kozeny-Carman 模型的假设是不合理的[20]，而且该方程不能有效地拟合渗透率试验值。进一步改进Kozeny-Carman 模型为

式中，n和C均为经验参数，n为使用除2 以外的指数，该模型并非基于流动机理，可作为拟合试验数据的经验模型[21]。

渗透率试验可分为饱和试验和非饱和试验两类。饱和测试通常测量流体在所选方向流动时，通过已经饱和的织物时的稳态流量和压降之间的比率。相比于干燥的纤维布，树脂在已经完全浸润的纤维中阻力更小，更容易流动，因此饱和试验的渗透率结果通常比非饱和试验结果偏大。然而真正的LCM 过程是非饱和的，前进的流动前沿是该过程的一个重要特征。根据树脂流动的维度，将其分为一维、二维和三维流动，相对应地测得不同的渗透率参数，如图2 中的面外渗透率测试[22]。由于饱和试验无法区分流动的维度，因此饱和试验通常会在精心设计的试验条件下进行某一特定方向的测量，即一维流动。而非饱和试验可以通过流动前沿监测技术同时获取树脂在不同方向上的流动前沿，因此非饱和试验可以在一个或多个维度下进行。

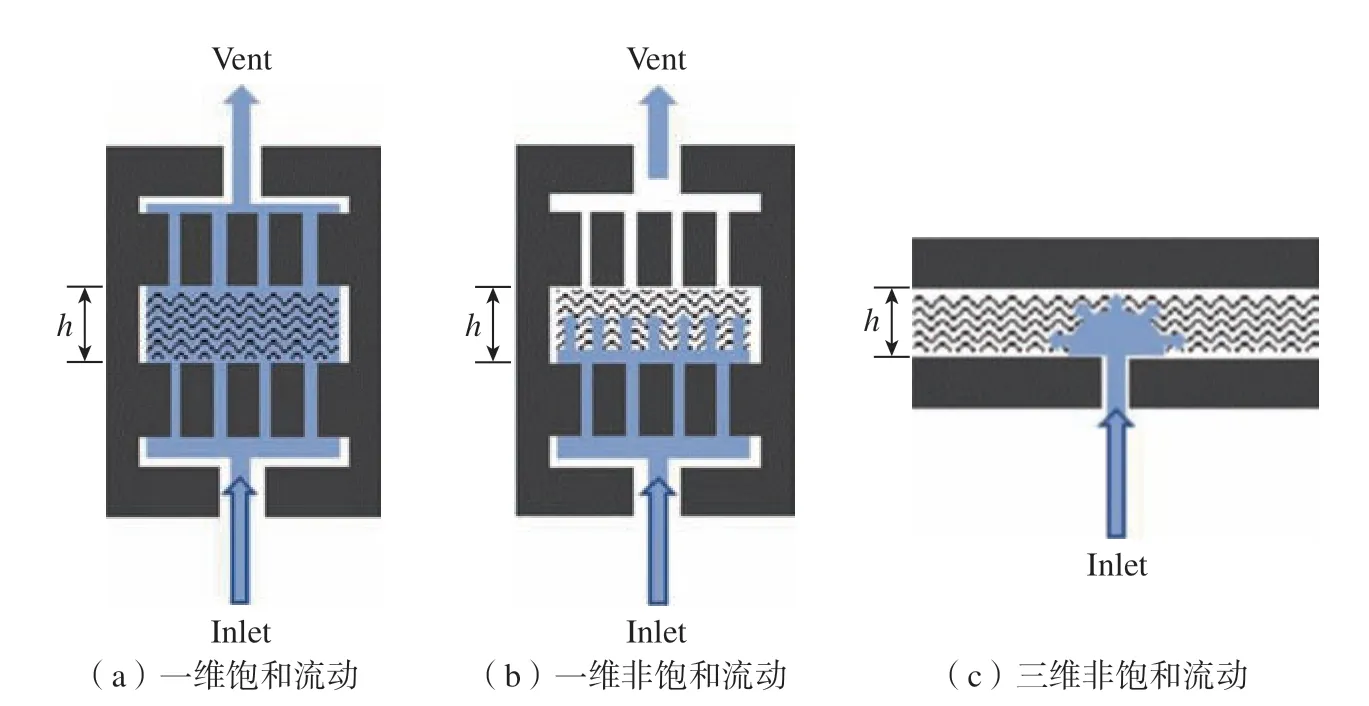
图2 面外渗透率测试试验示意图[22]Fig.2 Schematic diagrams of the principles of out-of-plane permeability measurement[22]

2 饱和渗透率试验

饱和渗透率试验通常为一维流动，其控制方程可以由达西定律的一维形式描述。

式中，Q为体积流量；A为流道截面积；Δp为试样两侧的流体压力差；h为试样厚度。对于饱和测试均为一维流动，即树脂仅在一个特定方向上流动。对于式 （5），必须首先建立稳态流动，即试样完全饱和且所有空气都从流道中被排开，当监测的流体压力和体积流量均稳定时，可以计算得到渗透率，因此不需要对树脂流动前沿进行跟踪。

2.1 一维饱和面内试验

一维流动指树脂仅在一个方向上流动，渗透率的3 个方向均可以通过一维流动进行测量。饱和一维面内试验指树脂在选定平面内某一方向进行流动，测试相应方向上渗透率，一般是线性注射，因此也可称为线性流动。Caglar 等[23]采用一维饱和流动试验研究了球形夹杂物对斜纹玻璃织物面内渗透性的影响，发现夹杂物含量越少直径越小，渗透率越低；夹杂物直径变大，会扩大现有孔隙或形成新的孔隙，增高渗透率。Comas-Cardona 等[24]通过在两个刚性压缩板上进行饱和浸渍的纤维压缩试验，结合数值仿真测量了面内饱和渗透率，结果与注入技术测得的渗透率值吻合。法国ONERA 机构和天主教鲁汶大学提出进行国际渗透率基准测试的倡议后，全球不同机构进行面内面外渗透率的基准测试，作为渗透率测量标准化的第一步，目的是概述实际使用的方法以及实施这些方法获得的结果范围。在第一次面内基准测试中，包括Verrey 和Laine 等在内的六家单位采用一维饱和面内渗透率试验获取相应方向上的渗透率[25]。

2.2 一维饱和面外试验

一维饱和渗透率试验主要应用于面外渗透率的测量，该方法只需要压力计和流量计，易操作实现。如图3 所示，Aziz 等[26]在饱和流动条件下使用万能试验机精准控制样品厚度，使用多孔板实现厚度方向上的一维流动，结合进出口压力传感器和流量传感器按式 （5）测量了干纤维的面外渗透率，发现自动式干纤维铺放过程中的工艺变量对渗透率的影响最高可达5 倍，确定了预制件的面外渗透率与自动化干式纤维铺放制造技术的工艺变异性之间的相关性。同时根据X-CT 扫描重建精确的TexGen 模型，与数值模拟技术相结合，得出了与试验数据偏差±10%的准确渗透率预测结果，建立预测渗透率的有效方法。

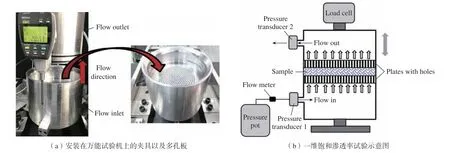
图3 一维饱和渗透率面外试验装置[26]Fig.3 1D saturated out-of-plane permeability experiment equipment[26]

根据一维饱和面外试验，Rimmel等[27]基于流量和压降测量评估了拼接对碳纤维预制体的面外渗透性的有利影响，由于缝合预制件微观结构中存在流动通道，可使渗透率提高近50 倍，且标准偏差较小。因此，缝合可以有效提高面外渗透率，从而提高干纤维铺放预制件的渗透性，与传统纺织半成品材料水平相当。Kabachi等[28]使用两个压力传感器和一个天平来监测压降和流量，在不同的纤维体积分数条件下，测定了3 种玻璃纤维增强材料：机织织物、非卷曲纤维和纤维垫，进而研究了循环压实对面外饱和渗透率的影响，结果表明，渗透率随纤维体积分数的增加而降低，而循环压实使织物嵌套密度增大，尽管不影响渗透率的数值，但降低了结果的标准差。Yang 等[29]对纤维预制体面外饱和渗透率进行了数值计算和试验评估，提出了一个无量纲系数“填充系数”来定量评价模具对厚度方向流动的影响。在饱和与非饱和流体中，测量的面外渗透率随着填充系数的减小而增大，当填充系数为1 时，即可得到本征横向渗透率。在国际上进行的面外渗透率基准测试中[22]，大多数参与者使用一维饱和面外渗透率测量方法，原理均为测量厚度方向上流动的流量与压降，但压力和流量监测方式、传感器位置、流体分散介质、样品夹持方式等试验细节有不同。单因素方差分析结果表明，压力监测方式、传感器位置、流量监测方式、边缘效应等对结果影响并不显著。基准测试提出几点建议优化测量方案：密封样品边缘减少流道效应；样品层数应尽可能多以减少层间的嵌套对渗透率结果的影响；注射压力需要足够高以确保流动速度可以精确测量；压力必须低于进一步压缩试样所需的特定压力。

3 非饱和渗透率试验

3.1 一维非饱和面内流动

与饱和渗透率试验不同，对于非饱和渗透率试验，必须对流动前沿进行实时监测追踪，众多研究基于不同的物理原理开发了许多流动前沿监测技术，按照传感器与试样的空间关系分为非侵入式和侵入式两类。当流动前沿被实时确定后，非饱和渗透率的计算同样可以用一维形式表示，即

式中，ε是纤维预制体的孔隙率；t是注射时间；lf（t）是特定测量方向上流动前沿距离注射口的距离。

Lionetto 等[30]借助摄像机这种非侵入式光学方法对真空辅助成型工艺下单向碳纤维面内不同方向的渗透率进行了测试。如图4 所示，Da Silva 等[31]采用一维非饱和面内试验研究了玻璃/芳纶/环氧等混杂复合材料的面内渗透率，发现不同玻璃织物的混合可以提高渗透性，并确定了协同效应。 Aranda 等[32]同样采用该方法测量纺织品在剪切变形下的渗透率，发现剪切角在15°范围内时，主轴的渗透率呈线性增加，次轴的渗透率呈线性下降；当剪切角大于20°时，两者的行为都是非线性的。在第二次国际面内渗透率基准测试中[33]，全球共12 个机构和研究小组使用一维非饱和流动这一特定的程序来测量和比较碳纤维织物的面内渗透率，其中纤维体积分数、注射压力和流体黏度等参数需使用相同的值，以最大限度地减少散射源。在遵守指导程序的情况下获得的数据之间的散点低于25%。然而，当一些参数与这项工作的特定程序不同时，结果会产生较高的离散，试验程序之间的差异可能是造成分散的原因，与测试条件的影响相比，人为因素可以忽略不计。

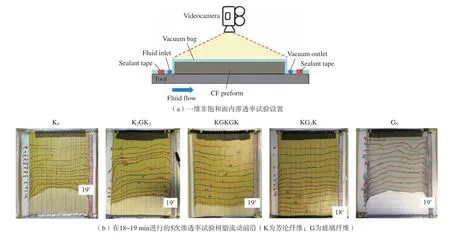
图4 一维非饱和面内渗透率试验[31]Fig.4 1D unsaturated in-plane permeability test[31]

部分研究者对比了一维流动下饱和与非饱和面内渗透率的差异。Ma 等[34]采用一维流动试验测量了5 种不同预制体的饱和与非饱和渗透率，试验结果表明，渗透率与孔隙率之间的关系可以近似地表示为指数函数。当孔隙率降至0.65 左右时，渗透率急剧下降。试验中所用织物的非饱和渗透率在试验条件下均表现出随着流动前沿向前移动而增大的特点，但其演变规律有所不同。不同材料非饱和渗透率与饱和渗透率的比值 （KUnsat/KSat）为0.4～ 0.7。Shojaei 等[35]通过单向注入试验研究了不同注射压力和纤维预制体孔隙率对玻璃织物饱和和非饱和渗透性能的影响。试验可以识别出树脂的最大平均速度，低于该速度时瞬态渗透率保持不变；饱和渗透率总是高于非饱和渗透率，其差异值在注入压力范围内保持恒定，且与纤维体积分数无关。Francucci 等[19]对比了单向流动试验条件下自然纤维的饱和与非饱和渗透率，发现饱和渗透率的值偏高，这一观察结果可归因于致密纤维束的延迟浸渍，相对于宏观流锋，由于束间和束内局部渗透率的差异，当微孔已经被流体填充时，流速减小；另一种可能的解释是纤维织物会从主流体中吸收更多的液体，减缓流体流动，从而增加流动阻力，降低渗透率。当预制体完全浸渍并被流体饱和，不再有微孔浸渍或流体吸收，流速增加，因此，饱和渗透率高于非饱和渗透率。Park 等[36]发现压力梯度在非饱和流动中是非线性的，具有正曲率，实际流动前沿处的负压梯度小于线性压力梯度假设下的预测值，如图5 所示，对压力梯度的误解是导致相同纤维预制体的饱和和非饱和渗透率差异的主要原因。此外，若流动前沿后面的纤维束没有完全饱和，则会有一部分液体流入纤维束，称为质量沉积效应，质量守恒方程失效。据此Park 等[36]提出3 点建议： （1）在模具中使用多个压力传感器以便获得不同位置和瞬间的局部压力梯度； （2）非饱和渗透率测量中，渗透率应通过流动前沿处的局部负压梯度来评估； （3）根据束间和束内流动修改质量守恒方程。

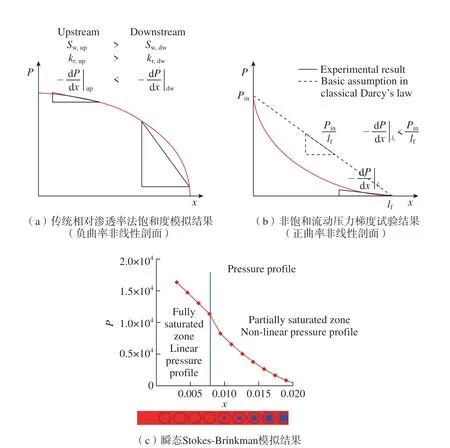
图5 常规建模方法（相对渗透率）与试验/模拟结果的压力梯度比较[36]Fig.5 Comparison of pressure gradient between the conventional modeling approach(relative permeability) and the experimental/simulation result[36]

3.2 二维非饱和面内流动

一维非饱和面内流动仅仅能获取纤维预制体某一特定方向的面内渗透率，而二维非饱和面内流动试验可以从单个试验中同时获取面内主渗透率K1、K2和旋转角β。在基准测试[37]规定的测试程序中，测试流体在恒定的注射压力下通过中央注射口注射到包含干燥纤维预制体的腔体中，其中预制体的中心通常有一个贯穿厚度的孔，对齐注射口以确保树脂在注射开始时尽快充满该孔，并在随后阶段均匀浸渍面内各层。该测试程序下液体流动前沿通常为椭圆形，因此也称为径向流动，如图6所示[37]。

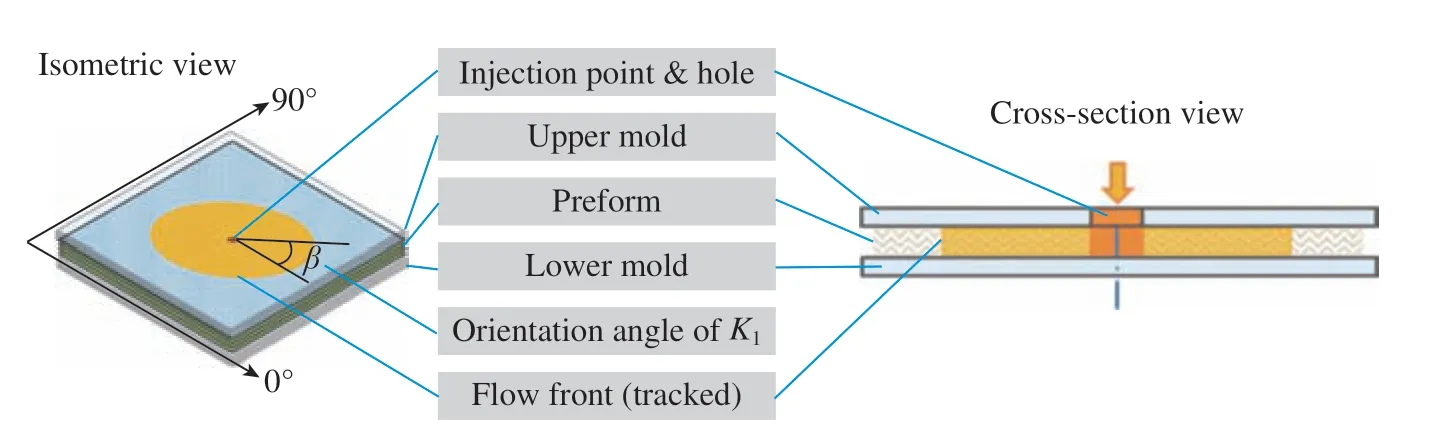
图6 径向注入方法示意图[37]Fig.6 Schematic illustration of the radial injection approach[37]

对于二维非饱和面内流动，在具有面内各向同性特性的纤维中流动时其流动前沿为圆形，其控制方程相对简单[38]。

式中，ρf=Rf/R0是无量纲半径；是无量纲时间；Rf是流动前沿距离注射口位置；R0是注射口半径。根据试验数据可以绘制一条过原点的拟合线，进而根据斜率得到渗透率数值。对于正交各向异性材料，面内渗透率张量简化为

在此条件下，需要将椭圆拟合到流动前沿的测量点上，并根据过程条件转换为等效的各向同性坐标系，将椭圆流动前沿转换为圆形，进而根据注射时间的变化计算渗透率值。对原坐标系中 （x，y）点到各向同性坐标系中 （xe，ye）点其转换方程为[39]

Weitzenböck 等[40–41]率先提出径向流动下获取面内渗透率的迭代算法，结果表明，该算法可以使渗透率结果的准确性和可靠性有明显提高，而且通过计算旋转角β，主渗透率值可以自动校正关于测量轴的任何偏差。此外，该方法中流动前沿测点的数量和时间步长都可以不同，不需要在同一时间对所有3 个流动方向（0°、45°、90°）进行测量，因此更加通用。在第一次国际面内渗透率基准测试中，Arbter 等[25]比较了16 个不同的试验程序获得的面内渗透率数据，发现不同的试验条件 （如线注射或径向注射、恒定压力或恒定流速边界条件、饱和与非饱和流动等）使在任何给定的纤维体积分数下，每种织物的主渗透率分散高达一个数量级，主渗透率值的比值变化系数可达2。试验的不确定性和样品的可变性会影响单一系列试验结果，为了实现测量方法的标准化和结果的普适性，为不同机构制定相同的试验标准可以有效消除散射源，这也是第二次基准测试[33]的结果稳定性较好的原因。对于无卷曲纤维，Grössing 等[42]采用电容式面内渗透率测量技术，研究了纺织参数对其面内渗透率的影响，结果表明，粗纱条数和所用针脚长度对织物的面内渗透性有影响，对纤维克重没有影响，据此可为选择特定渗透率数据的纺织品和数值模拟提供参考依据。对于机织织物，如图7 所示，Rieber 等[43]使用带有8 个线性电容式传感器的铝质模具对19 种玻璃纤维机织织物进行测量，考察了织法、线密度、纱线密度和卷曲对面内渗透性的影响。发现卷曲比越大的纺织品，其渗透率的各向异性也越大，渗透率–纤维体积分数曲线的斜率与线密度、纱线密度相关。机织织物的各向异性取决于经纬纱的卷曲比，且斜纹织物的面内渗透率各向异性更强。

图7 二维平面渗透率测量单元，下模具安装有电容式传感器[43]Fig.7 In-plane permeability measurement cell with capacitive sensors in the lower mold half[43]

3.3 一维非饱和面外流动

复合材料通常为薄壁结构，厚度在毫米量级，在沿厚度方向流动距离很短的情况下，其内部的流动前沿难以观测且测量点少，因此面外方向的非饱和渗透率测量比面内方向的渗透率更具挑战性。英国国家物理实验室牵头国际上26 个机构进行了纤维预制体面外渗透率的基准测试[22]，大多数参与者使用了一维饱和流动测试方法，而少数人选择了一维非饱和或三维非饱和流动方法，结果显示数据之间有高达两个数量级的散射。式（6）同样可以用来确定一维非饱和流动条件下的面外渗透率。

基于侵入式光纤传感器，Drapier等[44]将其末端剥除包层后用于监测厚度方向上的流动前沿位置，结合一维饱和[45–46]与非饱和面外流动，测量无卷曲多轴织物的饱和与非饱和面外渗透率。基于超声纵波方法，假设纵波在干燥和浸润的纤维内传播速度分别为恒定值，则沿厚度方向的流动前沿与超声纵波的飞行时间呈线性相关。Schmachtenberg 等[47]研究了超声波纵波技术在树脂流动前沿的应用，并利用超声波信号、传输时间和振幅实现在线监测。Stöven等[48]开发了一种基于超声纵波的三维流动前沿在线监测，实现纤维预制体内流动前沿瞬时位置的连续测量，并通过数值流动模拟软件确定了面外渗透率。此外，Becker 等[18]基于超声传感器对流动前沿进行监测，对包括碳和玻璃编织物及无卷曲织物两种体系在三个不同的纤维体积分数下测量其非饱和面外渗透率，结果表明，该体系与渗透率值的相对偏差符合较好，且大多在50%以下，纺织品引起的不均匀性和不同的测量参数 （如注射压力等）是导致偏差的主要原因。Konstantopoulos 等[49]采用超声纵波 （图8）对18 种不同预制件的面外渗透率进行了测定，系统重复性好且预制件纤维体积分数测量范围广泛，并通过视觉观测验证了超声法测量厚度方向上流动前沿的准确性。

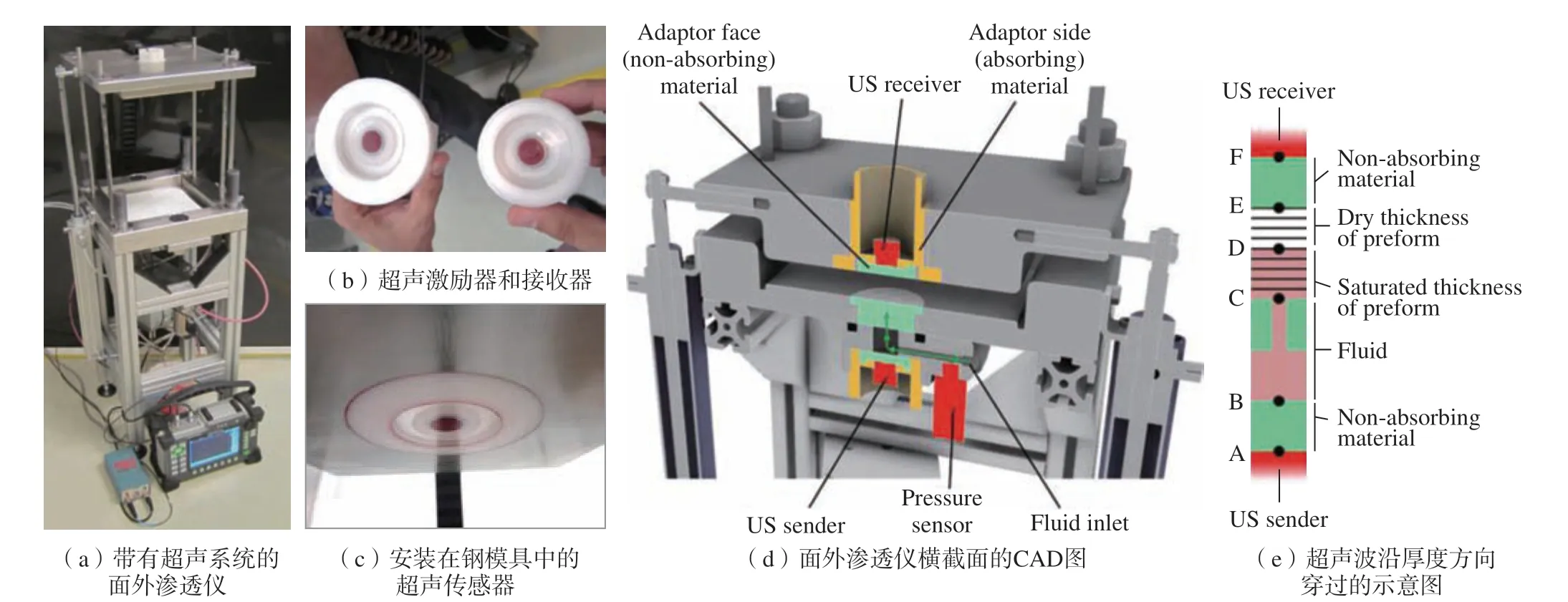
图8 带有超声系统的面外渗透率测量仪实物图和试验原理图[49]Fig.8 Opened transverse permeameter with the ultrasound system: Real device and schematic picture[49]

特别地，Kabachi 等[50]使用摄像机正对PMMA 管，在贯穿厚度的浸渍过程中直观地跟踪染色液体的流动前沿位置和纤维压实情况，同时使用压力传感器监测进口压力，试验设置如图9（a）所示；图9（b）为相应的试验结果，初始纤维体积分数为0.4 的无卷曲织物在1.5 cm3/s 的恒定流速下，分别在0 s、10 s、20 s 和30 s 时的面外浸渍图像。结果表明，该方法可以方便地跟踪流动前沿和观察浸渍过程中的液体–织物耦合作用，且适用于各种纤维材料，涵盖了非常广泛的纤维体积分数和厚度。通过在测量样品的不同角度使用多个摄像机，可以提供更多关于样品周围流动前沿的信息，有助于提高流动前沿测量的精度以及渗透率计算结果的稳定性。

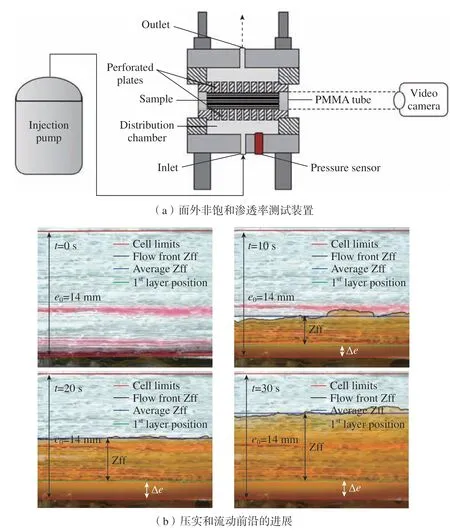
图9 基于摄像机和PMMA 管的一维非饱和面外渗透率试验[50]Fig.9 Through the thickness transient permeability measurement device based on camera and PMMA tube[50]

部分研究人员对比了一维流动下饱和与非饱和面外渗透率的差异。Ballata 等[51]将非饱和渗透率结果与Luce 等[52]的饱和渗透率结果进行比较，结果表明，玻璃纤维在饱和状态下测得的面外渗透率低于非饱和状态，KUnsat/KSat比值为4。Drapier 等[44]对无卷曲多轴织物进行一维面外饱和与非饱和渗透率试验，发现非饱和与饱和渗透率结果均取决于接收流体的织物面，非饱和渗透率比饱和渗透率大10 倍左右，试验结果可以为两种状态下渗透率预测的发展提供理论基础。在面外渗透率基准测试中[22]，对比了不同机构采取的一维饱和、一维非饱和与三维非饱和面外渗透率试验结果，发现在所有纤维体积分数下结果趋向于相同范围，当体积分数为0.47 时，三维非饱和试验得到的数值更高。使用一维饱和和一维非饱和试验的大多数参与者拟合得到的Kozeny 常数值在去除异常值后处于相同的范围内。对于三维非饱和流动试验，拟合系数值往往小于其他试验方法，表明该方法的数据一致性较差；同时得出，一维饱和面外渗透率测试结果近似LCM 加工中的非饱和流动的结论。

3.4 三维非饱和流动

3.4.1 三维流动前沿监测技术

在渗透率测量技术中，由于三维非饱和流动涉及3 个维度下的椭球形流动前沿，因此其流动前沿监测和理论模型是最复杂的。对于非侵入式测量流动前沿方法，其中成本最低且简便的监测方法是采用透明模具或真空袋进行纤维预制体压实，并视觉追踪流动前沿。Nedanov 等[53]使用摄像机捕捉树脂到达底层时的点；使用电子天平测量质量并结合达西定律计算三维流动前沿在纤维预制体内的分布，进而提出一种确定渗透率张量的非侵入式方法。Yun 等[54]建立了三维径向流动试验，采用两个摄像机记录预制体顶部和底部表面的流场分布，试验设置如图10 所示。尽管视觉追踪流动前沿操作简单、成本低、对结构影响小，但该方法需要刚度较低的透明模具，才不容易导致模具结构和纤维预制体出现大的挠曲变形，工程应用难度大。

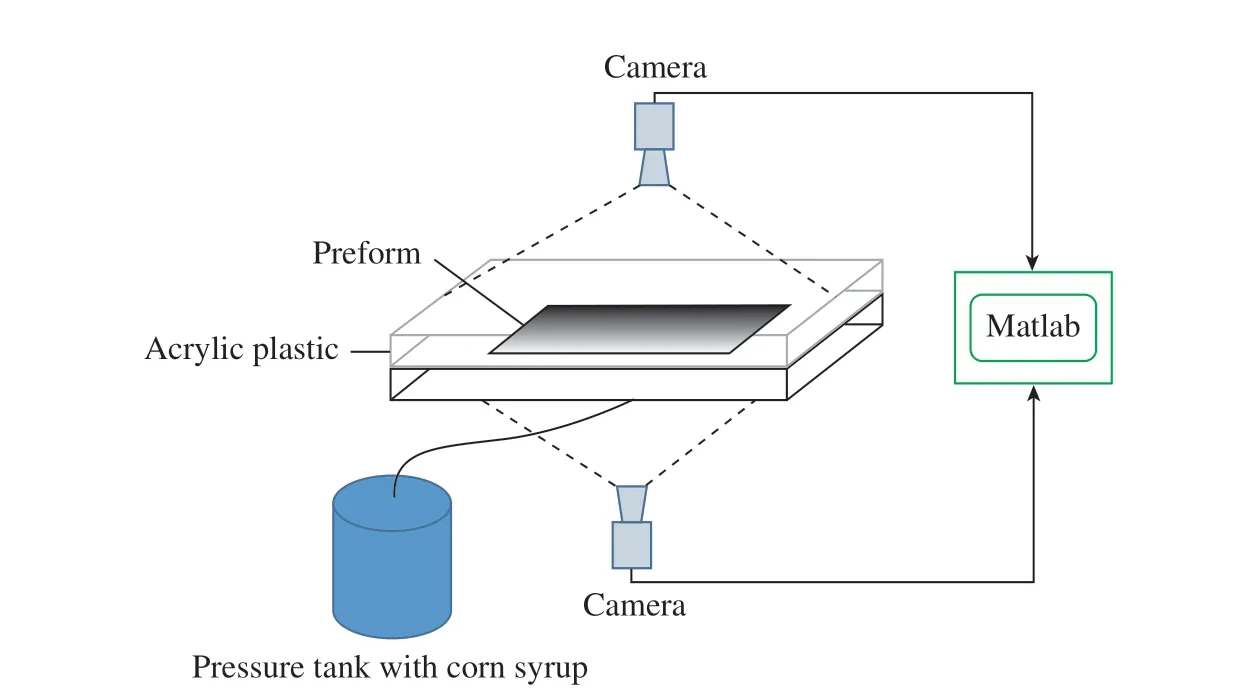
图10 单个试验确定渗透率张量的试验设置[54]Fig.10 Experimental set up to characterize six independent components of the permeability tensor of a fiber preform from one experiment[54]

对于非侵入式测量技术，通常要基于假设来间接获取实时流动前沿，易出现误差甚至错误。由于树脂到达干纤维前后会出现压力、热学、电阻抗甚至光学信号的变化，因此基于不同的监测物理量，学者们研究了多种侵入式流动前沿监测技术。液体在压力驱动下浸渍干燥的纤维预制体，因此压力传感器是一种常见的流动前沿监测技术。Di Fratta 等[55]提出了一种基于少量压力传感器和数值模拟相结合的树脂流动监测方法，在两个具有平面矩形和挡泥板状空腔几何特征的测试案例得到应用，结果表明，在不同的时间步长下，真实的流动前沿与估计的流动前沿轮廓线之间具有良好的一致性，并且能够充分检测到较小的流量变化。由于需要有足够的监测范围，因此压力传感器通常用于二维非饱和面内流动。对于热学传感器，Weitzenböck 等[56]使用热敏电阻确定三维径向流动测试条件下的树脂流动前沿，在同时进行压实试验确定纤维体积分数与压实压力的关系后，测量了三维渗透率张量，发现在三维流动的情况下，毛细流是主要的流动模式，毛细压力变得比外部施加的注射压力更重要，克服这一问题的唯一方法是提高注射压力。然而，过高的注射压力会导致流致压实和流道出现，使测量的渗透率值无效。Tuncol 等[57]使用热电偶传感器监测RTM 树脂流动过程，传感器成本低并且耐用，但存在高树脂流量、高比热、精度较低等限制，因此热学传感器并不优于其他传感器。

电阻抗类传感器监测原理是根据流动前沿到达前后传感器周围电阻抗的变化来感知纤维预制体内的流动前沿。Danisman 等[58]使用点电压传感器监测RTM 工艺过程的填充阶段，发现当流动的树脂覆盖传感器局部区域时，介质的输出电压增加。Ali 等[59]利用含有石墨烯涂层的压阻织物并基于压实期间的电阻变化来监测LCM 过程。Carlone 等[60]使用平行板介电传感器对玻璃纤维的一维树脂流动过程进行监测，但是当电/介电传感器与高规格复合材料部件制造中的主要对象 （碳纤维）一起使用时，极易出现电分选和电场干扰问题。针对此问题，Tifkitsis等[61]采用由两根规律扭曲的绝缘铜线组成的新型线性介电传感器来跟踪树脂流动前沿位置，其线性流量传感器如图11 所示。对于三维流动，Okonkwo 等[62]在顶部和底部模具上沿16 条径向线安装192 个电阻传感器 （图12），根据试验记录的树脂到达时间与三维流动模拟之间的相关性，使用黄金搜索法依次优化渗透率张量各个分量的值，所有平面内渗透率分量和面外渗透率都可以通过单一试验来表征。但是电学传感器通常为自制，缺乏设计标准且与导电纤维极易出现电场干扰问题，因此其推广和应用存在困难。

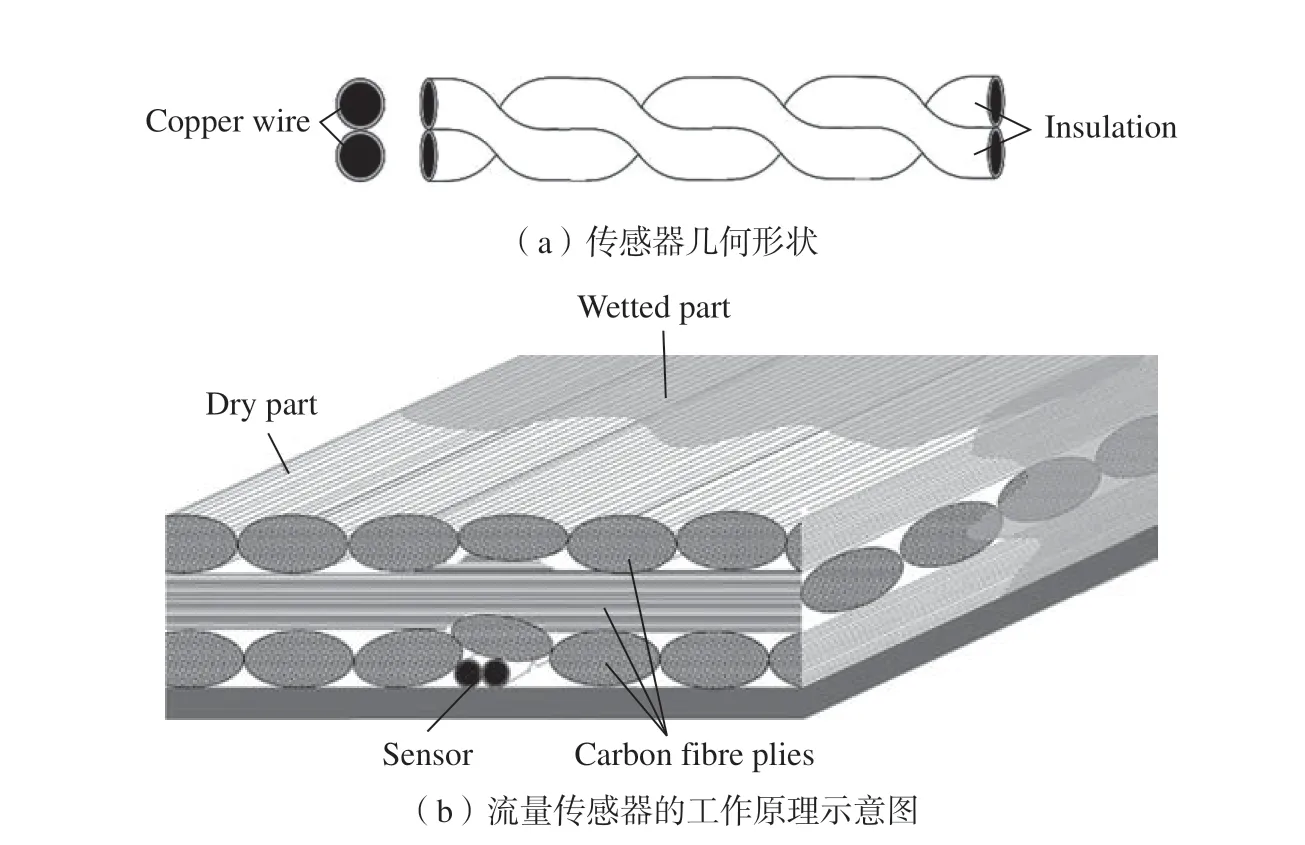
图11 线性流量传感器原理图[61]Fig.11 Schematic representation of lineal flow sensor[61]

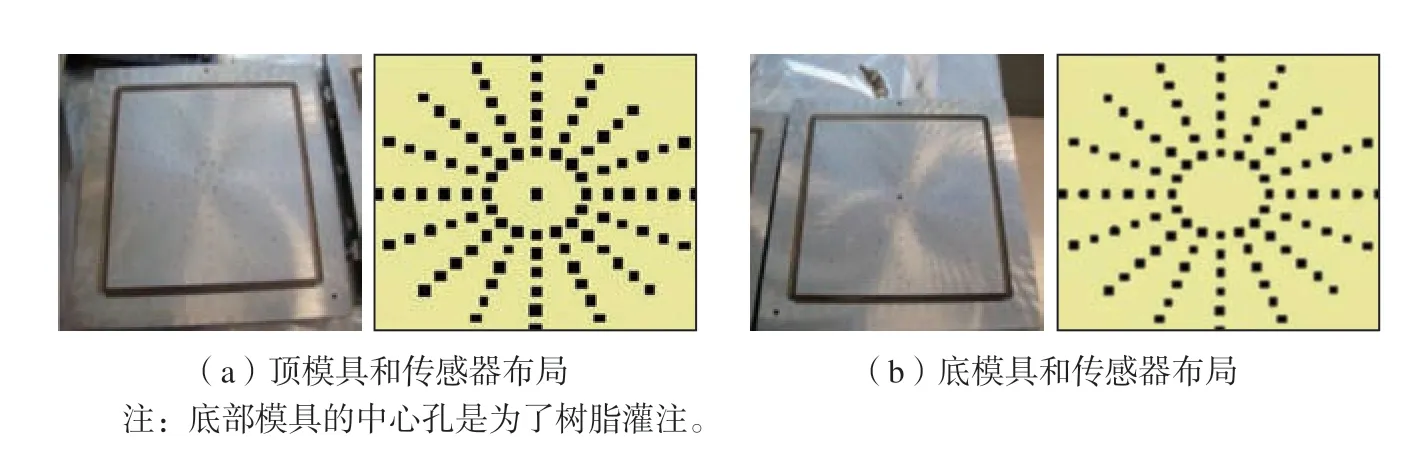
图12 线性安装电阻传感器的金属模具[62]Fig.12 Metal molds with resistance sensors linearly mounted[62]

由于重量轻、体积小、嵌入式干扰小，兼容导电纤维 （碳纤维）和非透明模具，不存在电场干扰问题，光纤传感器是一种理想的侵入式流动前沿监测传感器，受到了众多研究者的青睐。Eum 等[63]使用光纤布拉格光栅 （Fiber bragg grating，FBG）传感器内部的温度变化和长应变片内部的应变变化测量树脂流动前沿。Yu 等[64]在不同的层内嵌入多个FBG 传感器和压电传感器组成混合网络，相应测量结果相互补充并结合起来预测三维树脂流动前沿，在3 种不同厚度的厚碳纤维试件上，研究了所提出的混合传感器网络在不同位置的适用性，试验结果表明，该压电光纤混合传感器网络能够成功地对三维流动前沿进行原位和实时估计，实现智能健康监测。Antonucci 等[65]利用菲涅耳反射定律，通过检测光纤末端的反射光信号，获得三维树脂流动前沿位置，由于树脂流动到被蚀刻的光纤传感器位置时，其全反射条件会被破坏，导致光强信号下降，因此可以作为流量传感器监测流动前沿。Ahn 等[66]利用侵入式蚀刻光纤传感器来检测预制件内部流动前沿的位置，推导出三维流动下渗透率的表达式，比较现有光纤测量的渗透率和常规的压降与流量技术测量的渗透率，发现了很好的一致性。如图13 所示，Lim 等[67]使用了去除小包层段的蚀刻光纤传感器来检测局部流动前沿，并基于椭球形三维树脂流动假设计算3 个方向上的主渗透率值。同时开发了RTM 工艺的数值计算，计算结果与试验结果吻合，通过对一些实际案例的数值模拟，说明了其数值方法的有效性。

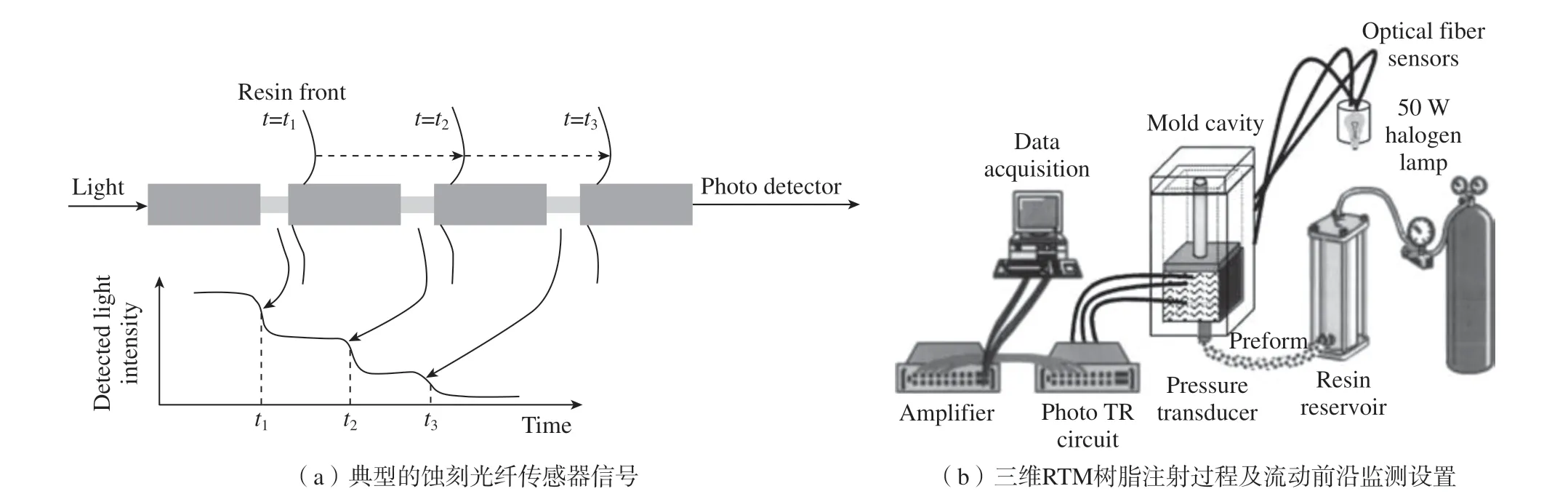
图13 基于蚀刻光纤传感器的三维RTM 树脂流动前沿监测[67]Fig.13 3D RTM filling process with etched optical fiber sensors[67]

综上所述，每种传感器有不同的优缺点。压力、热电偶传感器等点传感方法的传感范围小，在监测大样本时需要将传感器放置在多个离散位置，人力和时间成本高[68]。压力映射传感器[69]是一种平面测量传感器，可以用于获取树脂流动前沿到达时的预成形压力场，但对于大型结构来说成本仍然较高。光纤传感器脆弱且价格昂贵。电压传感器[70]、介电传感器和压阻织物通常为自制，设计成本高且难以推广，同时，这些传感器需要安装在模具内侧或者侵入到复合材料内部，脱模后会在复合材料表面留下痕迹影响成品质量。不同流动前沿监测技术的应用场景和优缺点如表1 所示。毫无疑问，摄像机记录技术仍然是最简单、最便宜和最有效的方法之一，光纤传感器则可以提供准确的内部流动前沿信息，是作为复合材料内部侵入式测试的首选传感器。

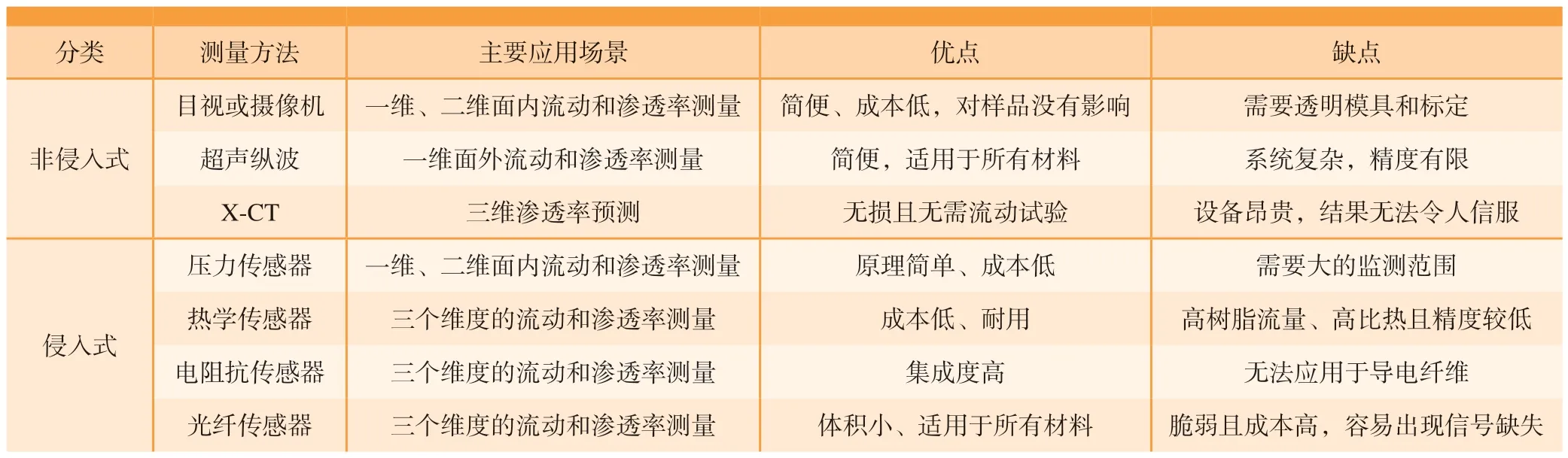
表1 不同非饱和渗透率测试中的流动前沿监测技术Table 1 Different flow front monitoring techniques for unsaturated permeability tests

3.4.2 三维渗透率计算方法

在实时获取三维树脂流动前沿后，需要对面外渗透率建立理论模型和相应计算方法。

第一类算法是解析法，即基于特定假设并通过三维流动的特点推导其解析解。基于达西定律，假设点注射条件下半椭球注入口会在靠近注射口形成半椭球流，可以推导出表2中方法一的方程，使用试验测得的特定流动时间厚度方向上的流动前沿位置结合虚拟注射半径计算得到渗透率。而在实际应用中，很难建立这样的特殊注射口，半球形的注射口则较容易实现，然而该条件下不能得到封闭形式的解析解。因此，假设厚度方向上与注射口半径R0相关的虚拟半椭球入口半径为r0，该值从试验中很难直接测量，为了方便起见，假设r0=R0或者r0= 0.1R0。对于不同的材料，其最终的流动形状不同且在测量之前未知，因此几乎不可能在纤维预制件中精确地实现半球形缺口。为了解决这一问题，采用入口半径函数来确定该虚拟半径，等效入射口半径由注入流体质量计算，如表2 中方法二所示。然而，上述方法并不准确，因为实际试验或工程应用中注射口的直径通常与薄的纤维预制体厚度相当，甚至更大，因此点注射的假设难以推广应用。为了克服这一问题，Mekic 等[71]建立了径向注射模型，并通过笛卡尔坐标系向扁椭球坐标系的非线性变换得到横向渗透率的解析解，如图14 和表2 中方法三所示，在已知面内等效渗透率的基础上实时获取三维流动前沿测点计算得到三维渗透率。当预制体的厚度远大于注射口直径时，近似于点源解，方法三可化简为方法四的渐近形式。在此基础上，Mekic 等[71]提出了一种利用该解析解直接从试验数据中计算面内和面外渗透率的试验方法，用于预测和理解复合材料液体成型过程中的树脂流动行为。

表2 基于三维非饱和流动下的面外渗透率计算方法Table 2 Out-of-plane permeability calculation methods based on 3D unsaturated flow

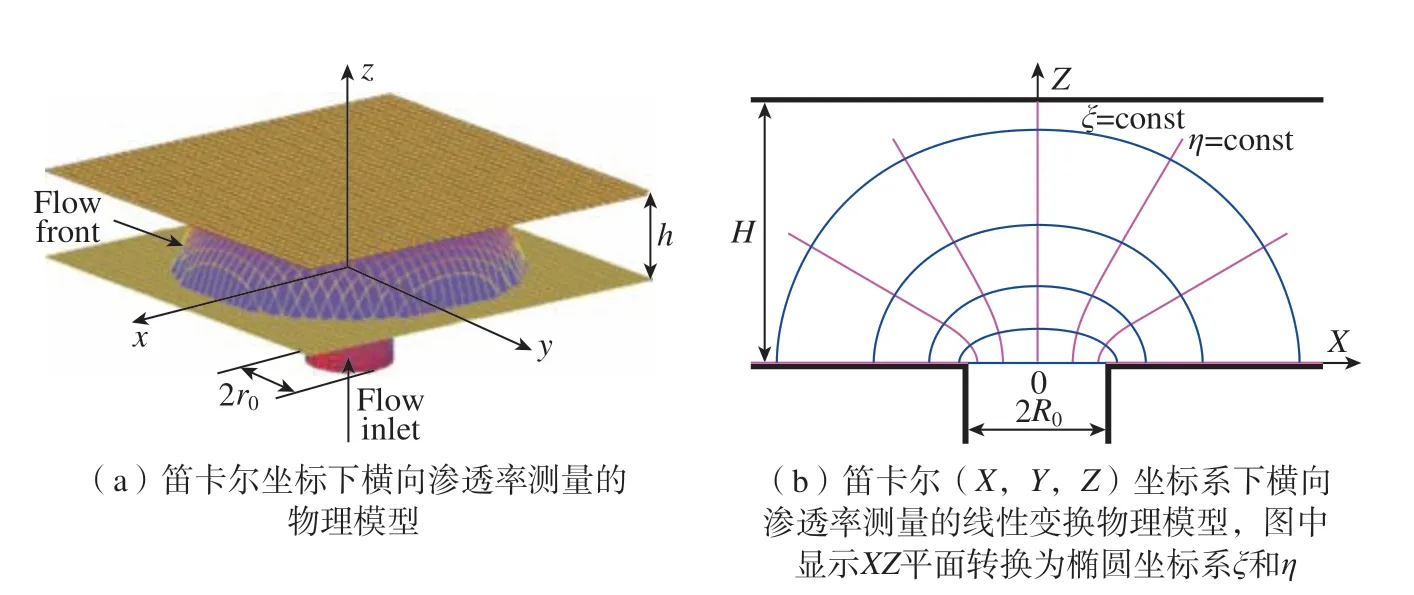
图14 基于径向注射的三维渗透率物理模型[71]Fig.14 Physical model for transverse permeability measurements based on the radial infusion [71]

第二类算法是流动前沿监测试验结合其他流动模拟软件的优化算法，通过优化例程改变模拟中的渗透率分量，寻找试验和三维流动模拟之间的最优解，在所有传感器位置实现与试验到达时间的最佳匹配。Yun等[54]建立三维径向流动试验，通过图像处理算法自动提取各个位置的流动前沿到达时间，使用流动前沿随时间的位置数据，将其与优化算法和流动模拟工具LIMS（液体注射成型模拟程序）耦合，从单个试验中求出渗透性张量的所有6 个独立分量，其过程是自动化的，将试验结果叠加在仿真结果上，以确认渗透率值的保真度。图15 所示为Okonkwo 等[62]在迭代优化算法中使用黄金搜索法依次优化渗透率张量各个分量的值，然后重复整个序列，直到找到树脂流动前沿到达的最佳匹配，获得最小残差（RSS），其计算公式为

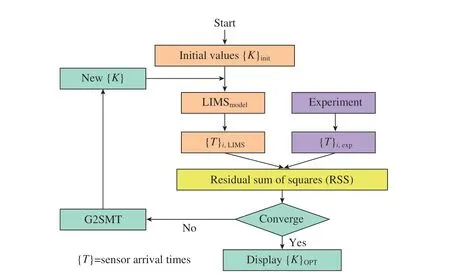
图15 比较试验数据和数值模拟确定渗透率值的流程图[62]Fig.15 Flow chart to determine permeability values by comparing experimental data with numerical simulation[62]

同时使用该技术演示如何通过在注入孔处使用分布介质来减少面外渗透率的变化，以避免纤维束堵塞入口，探讨该方法的有效性和灵敏度，结果表明，该技术有望通过单个径向流动试验来表征所有渗透率张量的分量。Antonucci 等[72]通过真空灌注试验，以及光纤传感器监测具有不同拼接特征的各种干纤维预制体的浸渍情况，同时基于商用PAMRTM 处理模拟程序，用数值程序拟合了由传感器信号获得的试验浸渍时间，进而测定单向缝合碳纤维预制体的面内渗透性和面外渗透性。结果表明，预制件的拼接特性不影响面内渗透性，面外渗透率与纤维面积重量和预制件的缝距呈递增关系。辅助导流体系具有更高的渗透性，因此对平面流动有较大的影响，并能促进树脂在层间的均匀渗透。Turner等[73]使用牛顿法确定纤维预制体渗透率张量，为适当的材料提供了高度可靠的结果；灵敏度分析表明，采用牛顿法是一种相当稳健的方法，其鲁棒性与试验误差有关，在牛顿法求解的方程组中包含线性方程是适当的，但不是必要的，线性方程可以隐式求解，并从系统中移除，从而减少未知数的数量。

第三类算法是非侵入式测量技术X 射线层析成像预测算法，通常基于纤维预制体的X 射线扫描图像生成精细的三维模型，并通过模型或者数值求解流体动力学控制方程对渗透率进行预测，其预测流程如图16 所示[74]。

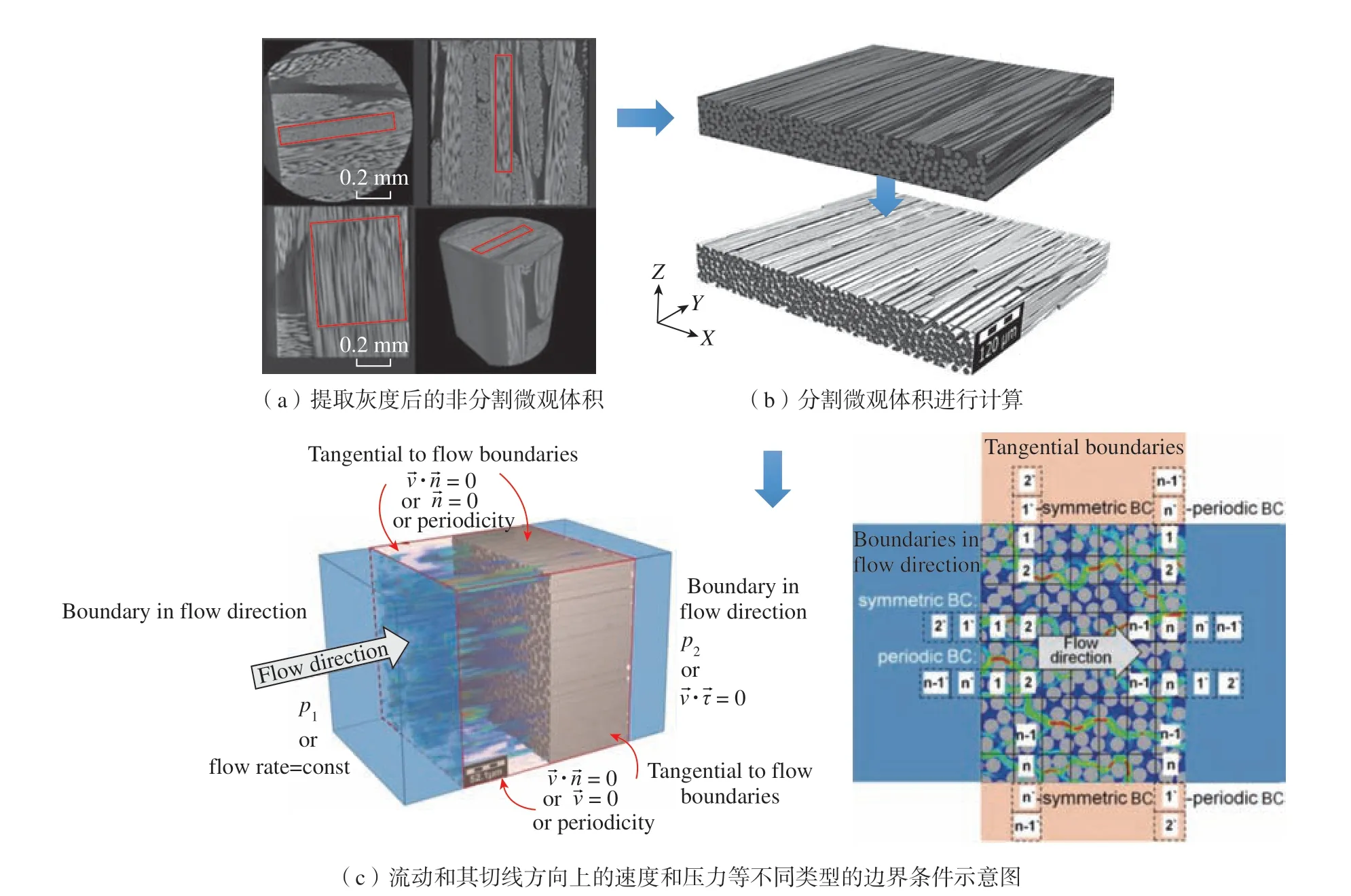
图16 基于X 射线扫描图像和数值方法的渗透率预测方法[74]Fig.16 Permeability evaluation method based on 3D X-ray microscope scan and numerical method[74]

Delerue 等[75]将渗透率假设为纯几何参数，以X 射线测得的三维几何结构作为输入，使用孔隙网络模型对纺织增强材料的均匀渗透率进行计算，在玻璃编织层压板验证结果，与试验测量值吻合较好。Ali 等[76–77]采用原位X 射线试验装置在压缩试验中对复杂的3D 编织角互锁织物进行了详细的流动路径分析，结合获得的层析图像中预测了不同纤维体积分数值下3D 正交和角度互锁碳纤维织物的面内和面外渗透率，发现树脂流动路径和主渗透率值与扫描图像的纤维体积分数密切相关，预测的渗透率值与传统的基准试验数据吻合较好，并利用修正的Kozeny-Carman 关系推导了体积分数与渗透率的关系。同样， Ghafour 等[78]通过面外压缩试验，使用X 射线对两种亚麻纤维垫的微观结构进行分析，利用三维图像作为输入数据，计算了所研究纤维垫的渗透率张量的主分量及其在压缩过程中的演化，模拟结果表明，渗透率呈横向各向同性，主轴在压缩过程中不演化，同时提出了修正Kozeny-Carman 模型。在2023 年举行的在微观尺度上基于图像预测纺织品渗透率的基准训练中[74]，共有16 名参与者使用不同的数值方法、边界条件和渗透率识别技术提供了50 个结果。消除不一致结果后，预测面内渗透率的散射 （14%）小于面外渗透率的散射 （24%），结果表明，影响渗透率的主要因素是切向边界条件、重整化方法中使用的子域数量和渗透率识别技术。基准测试提出几点建议：为了解决多孔介质渗透率预测中的蠕变流动问题，应采用Stokes 方程；对于主方向未知或具有各向异性效应的微结构，不适合采用对称或无滑移边界条件；由于渗透率是一个对称的正定二阶张量，因此对于渗透率识别，使用一种允许计算全渗透率张量的方法至关重要。

4 未来发展趋势

渗透率是复合材料液体制造工艺树脂灌注阶段的关键参数，对复合材料制造阶段的干斑缺陷和最终成品质量有重大影响，同时也是流动模拟的决定性输入参数，因此对纤维预制体渗透率的准确测量是提高复合材料生产效率和质量的关键技术。综合以上的研究，其未来发展趋势如下。

（1）渗透率试验多参数化变量的控制与监测。

渗透率试验测量参数众多，如饱和流动试验的液体流量、黏度、注射压力和非饱和流动试验的流动前沿、压实压力等，以上参数对其试验结果均有很大影响。国际上的面外渗透率基准测试[22]对包括测量方法、注射压力、厚度控制技术、样品几何形状、分散介质、样品厚度等诸多因素对试验结果的影响进行了分析；面内渗透率在遵循相同指导程序的情况下标准偏差约为20%，面外渗透率则有最高达两个数量级的散射，如在49% ～ 51%纤维体积分数下平场织物的面外渗透率测试结果最大相差100 倍。因此试验者仍需对多种参数进行变量控制和监测，以确保试验的顺利进行以及结果的准确性和可重复性。

（2）基于不同原理的多传感技术的集成。

由于要对渗透率试验过程多个参数进行测量，单个传感器无法满足试验需求，因此需要众多传感技术的协同应用，例如压力传感器、位移传感器、流量传感器、超声传感器、光纤传感器等。基于力学、声学、光学等不同原理的多传感技术需要协同运作且互不影响，确保试验过程中多参数的准确测量与控制，通过多传感数据的融合以获取稳定可靠的渗透率结果。

（3）基于实际工业应用场景的标准化测定程序。

国际上已经进行了针对面内和面外渗透率的基准测试，参与者们力争在相同材料下以尽可能相同的试验程序确定渗透率结果，以期减弱结果分散性，其中二维径向流动下的面内渗透率国际测量标准已经建立[79]，而面外渗透率由于散射过大，标准一直无法确立。本文认为应结合实际的工业制造应用场景，制定基于一维或者三维非饱和流动对应的测定程序，将测量结果反哺应用到工业制造过程中，建立不同应用背景下的测定程序标准。

（4）渗透率测试、流动仿真、试验以及实际LCM 工程应用之间的匹配优化。

渗透率参数作为输入性参数对流动仿真技术提供指导，建立基于实际应用的试验和仿真技术，首先应减弱甚至消除有限元网格及边界条件对结果的影响，确保仿真结果的准确性；其次将渗透率作为优化指标，采用迭代优化或机器学习算法实现仿真与试验结果的最佳匹配。在批量生产制造中提供生产指导和反馈控制，实现高质量、高产能下的智能制造。

5 结论

21 世纪以来，纤维预制体的渗透率测量技术百花齐放，国际上许多国家的研究机构参与了这项具有挑战性的基准测试工作，众多研究者在试样准备、试验方法、流动前沿测量技术及理论计算等多个部分做了许多原创性工作。本文着眼于纤维预制体渗透率测量技术，根据流动维度分为一维、二维、三维流动，根据流动状态分为饱和与非饱和流动，非饱和流动的重难点在于流动前沿实时监测技术；结合不同的测量技术、试验条件以及计算方法和国际上进行的面内面外渗透率测量及图像法预测等基准训练，分析了渗透率结果分散性大等问题，需要建立渗透率各分量测量的国际化标准。

我国正处于智能制造的关键时期，复合材料液体成型技术成本低，且适用于制造大尺寸三维复杂结构。关于其渗透率的研究需要众多研究者在渗透率测量试验、多传感技术融合以及流动仿真等方面进行学科交叉研究，共同为复合材料制造技术发展以大批量生产应用贡献力量。

致谢

感谢比利时Katholieke Universiteit Leuven 材料工程系的Stepan V. Lomov教授、Jan Ivens 教授和Pedro Sousa博士在纤维预制体渗透率学习方面的指导和帮助。