改善同塔混压双回直流输电线路电磁环境研究
戚无限,郝思鹏,周叶,荀道玉
(南京工程学院 电力工程学院,南京 211167)
引言
我国资源分布和经济发展的不平衡,需要建设大规模、高容量的高压直流输电线将中西部电能输送到东部地区。超高压±500 kV 与特高压±800 kV 直流输电适合中、远距离输电,两者同塔建设能够优化资源配置,实现对不同距离和不同负荷容量的电能输送[1-2]。多电压等级混合和输送功率的提高,线路的电磁环境影响愈发显著。文献[3]通过增加线路间距和对地高度来改善直流输电线路的电磁环境。文献[4]采用改变输电线路分裂间距和数量的方法减弱电磁环境影响。文献[5]提出对高压直流线路下方增添屏蔽线的的方法来减弱线路电磁环境。本文提出改变直流输电极导线的空间布置方式,重构极导线电晕后正负离子的空间分布数量状态来改善直流输电线路的电磁环境影响。现有双回混压直流输电线路大多数采用的是“干”式杆塔,上层横担架设±800 kV 输电线,下层横担架设±500 kV 输电线。“干”式杆塔由于两极导线水平距离的限制,会占用较宽的输电走廊。为减弱电磁对环境影响和减少线路走廊宽度,将架设的±500 kV 输电线由水平排列变为垂直排列。考虑到杆塔高度和建设经济成本,上层横担架设的±800 kV 输电线需保持原有的水平排列,但可以改变导线间水平间距和导线离地高度。
以酒杯直线塔为基础,针对输电走廊狭窄地区,提出三种双回直流输电线路布置方式,拓展直流输电线路排布方案。新方案下高压直流线路由于几何架构变化,其电晕效应、电磁环境与常规布局相比存在一定差别;对高压直流输电线路的方案布置进行研究,这对其安全电磁环境和未来线路杆塔架构变化趋势具有重要意义。本文基于Kaptzov 假设的有限元解法对新方案布置下高压直流线路的地面离子流浓度、合成场强、走廊宽度以及风速影响等方面进行了研究分析,并对比常规布局下的电磁环境,选取新方案布置的较优方案并提出改善建议。
1 同塔双回直流线路布置
文献[2]提出±800 kV/±500 kV 同塔常规布局以±800 kV 线路为上层线路,其电磁环境影响较小,常规布局方式如图1 所示。因此,文中方案布置方案选取±800 kV 线路为上层水平线路,±500 kV 线路为下层垂直排列线路。
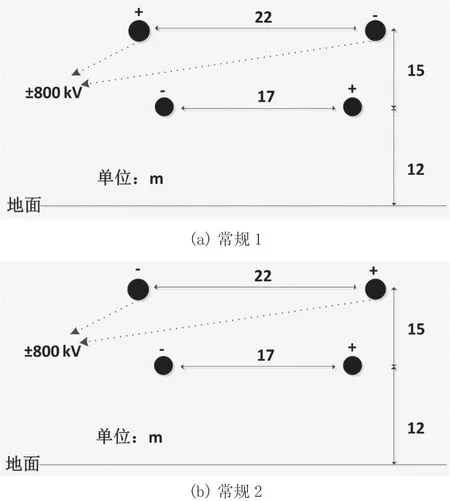
图1 混压直流常规布局
1.1 杆塔结构
考虑到新方案布置下杆塔的建造难度和经济成本,文中提出的直流输电导线新方案布置以酒杯型直线塔的导线垂直排列为基础,拓展酒杯型直线塔的双回导线布局,同时构建双回复合型酒杯直线塔,具体杆塔结构如图2 所示[6]。根据《±800 kV 直流输电架空线设计规范》,±800 kV 导线推荐采用夹角为(90~120)°的V 型绝缘子串;±800 kV 导线空气间隙取5.6 m。为了后续对比常规布局下的电磁环境,新方案布置下导线的最大高度不超过常规布局下导线的最大高度且最低导线高度相同。

图2 双回复合型酒杯直线塔
1.2 新线路布置方案
结合上述的杆塔形式和原“干”式塔线路布置条件,为了减少输电走廊宽度,文中计算的±800 kV/±500 kV同塔混压方案布置方式主要考虑三种布局形式,如图3所示。

图3 混压直流线路新布置方案
方案1 将原±500 kV 线路垂直排列,±800 kV 线路保持原水平间距且离地高度取最低限值21.5 m。方案2 在方案1 的基础上将±800 kV 线路离地高度保持与原“干”式杆塔布置下相同。方案3 在方案2 的基础上缩减±500 kV 线路垂直排列距离。
新方案布置和常规布局采用的导线参数相同,具体参数见表1。

表1 导线参数
2 电磁环境计算及限值
2.1 电磁环境限值
考虑到特高压直流输电作为长距离高跨度的输电骨干线路,大多建于野外以及非居民区,因此文中±800 kV/±500 kV 同塔双回混压直流线路采用的电磁环境限制为GB 50790-2013《±800 kV 直流架空输电线路设计规范》中对非居民区的电磁环境限值的规定,具体限制如下:晴天时地面合成电场不超过30 kV/m,最大地面离子流浓度不超过100 nA/m2[7]。
2.2 计算方法
李凌燕、杜志叶等学者从±800 kV/±500 kV 同塔双回混压直流线路常规布局的角度,基于Deutsch假设的电力线解析法,对不同极导线排列方式下±800 kV/±500 kV 混压双回直流线路的电磁环境进行了详细的分析[8]。基于Deutsch 假设的电力线解析法,可以将二维模型简化为一维模型进行求解地面离子流浓度和合成电场。本文所用基于Kaptzov 假设的有限元解法无需简化线路模型,相比于基于Deutsch 假设的电力线解析法具有更高的严谨性和科学性[9,10]。
文中采用有限元法计算同塔双回混压直流线路的离子流密度和合成电场。此方法求解过程中运用了Kaptzov假设。Kaptzov 假设认为导线起晕后,导线表面场强保持起晕场强不变,即E0=Ec(E0为起晕场强,Ec为导线表面电场强度)[9]。
高压直流输电线路普遍使用Peek 公式计算线路起晕场强,其公式如下所示:
式中:
E0—导线起晕场强;
m—导线粗糙系数(一般取0.47~0.6);
δ—空气相对密度;
req—分裂导线等效半径。
直流输电线路的合成电场和离子流场可由麦克斯韦方程组表示:
式中:
Es—合成电场;
ρ—离子电荷密度;
ε0—介电常数;
J—离子流密度;
µ—离子迁移率。
2.3 计算模型
文中采用Comsol 软件进行建模仿真,由于杆塔以及周围树木会使电场和离子流分布在其表面发生畸变,但畸变电场和畸变离子流分布不作为文章研究的重点,因此假设直流输电线路不受杆塔影响并将其转化为二维模型考虑[12]。文中在COMSOL 中以静电模块和稀物质传递模块构建耦合物理场对离子流场和合成电场进行求解。
在COMSOL 中使用有限元法求解离子流场和合成电场这类非线性问题时,其网格划分的精细程度决定了其计算精度以及计算量[13]。综合考虑直流输电线路模型实际情况,文中对仿真模型的网格划分采取内密外松的方法,即在导线表面及其周围采取高密度网格;在导线较远及其边界采取稀疏网格。以方案3 为例,有限元网格划分图如图4 所示。

图4 有限元网格划分
3 离子流密度和合成电场计算
文中采用Kaptzov 假设计算离子流密度,需自行初定导线表面电荷密度 0ρ,其表达式如下所示:
式中:
U0—起晕电压;
Es—地面最大标称场强;
U—导线运行电压;
h—导线高度。
判断是否满足Kaptzov 假设以及空间电荷密度是否收敛的判断公式为:
式中:
ρs(n)—第n 次迭代的导线表面电荷密度;
Emax—导线表面最大电场强度。
直流线路表面电荷密度迭代方程为:
3.1 方案布置下离子流浓度和合成电场
离子迁移率是合成电场和离子流场计算中重要的参数,事实上它会受到电场强弱,大气状态等影响,但文中主要关注于地面区域,场强相对较小,迁移率受其影响不大,所以计算中认为迁移率恒定。根据有限元理论,基于COMSOL 静电模块和稀物质传递模块,设置正离子迁移率为1.5×10-4m2/(V·s)负离子迁移率为1.7×10-4m2/(V·s),离子复合系数2×10-12m3/s[14,15]。方案布置下直流线路地面离子流浓度和合成电场横向分布曲线如图5、6 所示,其最大值如表2 所示。
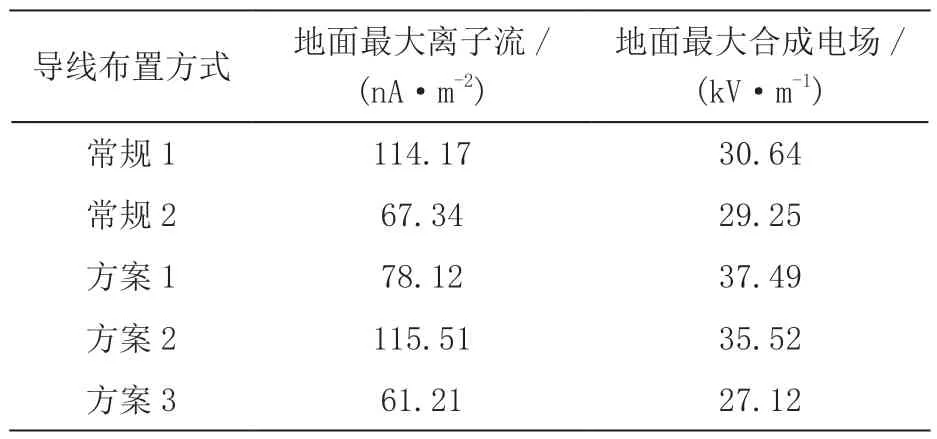
表2 各布置下地面最大离子流浓度和最大合成电场

图5 各布置下地面离子流浓度
由图5 可知,方案布置下地面离子流浓度在杆塔左右的变化不再为对称趋势。由表2 可得,常规2、方案1以及方案3 的地面最大离子流浓度满足非居民区限值要求。在方案布置中,地面离子流浓度最低的是方案3,地面离子流浓度峰值为61.21 nA/m2,其峰值位置出现在杆塔的右侧区域;杆塔左侧区域的峰值地面离子流浓度仅为9.58 nA/m2,比右侧离子流浓度低84.34 %,这是因为在新方案布置中线路左右两侧正负极性不同所致。
比较表2 中各最大合成电场,符合非居民区地面场强最大30 kV·m-1限值要求的只有常规2 和方案3。由图6 可知,新方案布置下地面最大合成电场也呈现出不对称性。杆塔右侧为地面合成电场峰值区,其中方案3的合成电场最小,为27.12 kV·m-1,优于常规2 布局下29.25 kV·m-1的合成电场峰值,较常规2 低7.28 %。在杆塔左侧区域,方案2 和方案3 的地面合成电场峰值要小于右侧;其中方案3 的左侧合成电场仅为14.73 kV·m-1,较右侧合成电场峰值低45.68 %。
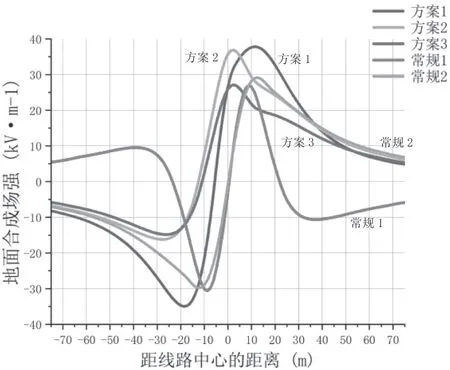
图6 各布置下的地面合成电场
综合上述各布置下地面离子流浓度、合成电场的比较分析,方案3 通过改变直流输电极导线的空间布置能够有效改善直流输电线路的电磁环境,并且形成一个电磁影响较弱的低值域侧。
3.2 空间离子分布状态分析
由于改变了直流输电极导线的空间布置,极导线电晕后所产生离子在空间中的分布状态也随之变化。直流输电线路电晕后离子在线路周围空间的分布密度和范围是离子流浓度、合成电场的关键影响因素。常规2 和方案3 的离子分布状态如图7、8 所示。
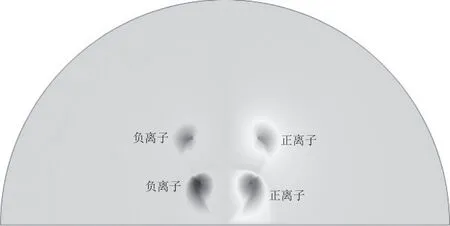
图7 常规2 布置下离子分布状态
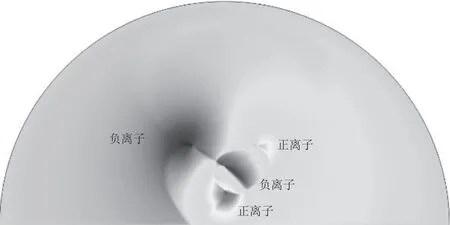
图8 方案3 布置下离子分布状态
常规2 布局下极导线同侧为同极性,在电晕后正负离子沿线路中心成对称状态,在线路中心区域发生正负离子中和反应。由于线路同侧的离子极性相同,空间分布状态因同极性离子互斥而扩散,使合成电场在线路中心远端的收敛趋势变缓,但同侧同离子的分布状态会产生一定的屏蔽性作用,降低离子流浓度和合成电场的峰值。
方案3 改变了极导线的空间布置,离子空间分布状态不再呈现对称。垂直排列中负极性导线电晕后产生负离子中和右上方以及下方极导线电晕后产生的正离子,并与左上方负离子形成屏蔽作用,减弱了右侧线路的电磁影响。左上方负离子由于同极性间的扩散作用,与垂直排列中正极性导线电晕后产生的正离子发生中和反应,降低了左侧区域离子流浓度和合成电场,形成不对称电磁环境中低值域侧。
3.3 走廊宽度
高压直流输电线路走廊宽度的关键因素是线路的合成场强,线路走廊宽度按照极导线靠近居民区时居民房屋所处地面处最大未畸变电场不超过15 kV/m 的标准确定最大走廊宽度[16]。文中常规布局和新方案布置下各线路走廊宽度如表3 所示。

表3 线路走廊宽度
由表3 可知:不同线路布置下的走廊宽度差别较大,常规2 布置下的走廊宽度最大,约为其余布置下的两倍宽度,这主要因为是常规2 布局下杆塔同侧导线为同极性,电晕放电后离子为同极性,从而导致合成电场衰减较慢,加大了走廊宽度。方案3 下的走廊宽度最小,仅为31.5 m,优于所有常规布局,适用于输电走廊狭窄区域;并且方案3 的左侧区域地面合成场强均小于15 kV/m,整体区域均满足居民区合成电场限值。从图6 中方案3的合成电场趋势来看,其合成电场具有不对称性,左侧合成电场总体上远小于右侧,且收敛速度大于右侧。在直流输电线路经过居民区外围时,可以考虑使用线路方案3 布置,将低合成电场侧靠近居民侧,可在一定程度上节约走廊资源、降低工程造价以及减少线路强拆区域范围。
4 风速对合成电场影响
在地面离子流浓度、合成电场和走廊宽度的比较中,方案3 布置下的各项电磁影响指标均为最小,故选取基于方案3 的导线布置方式来研究不同风速下合成电场的变化。
4.1 不同风速下的变化分析
特高压直流输电线路基本建于空旷的野外,环境中对合成电场影响最常见的因素是自然风[17]。文章在耦合物理场中设定横向匀速风,分别沿X 轴正负方向定风速w 为1 m/s,3 m/s,5 m/s,7 m/s 和9 m/s。图9、11 显示了方案3 布局下在不同风速下的合成电场变化趋势。

图9 方案3 左侧风不同风速下的合成电场
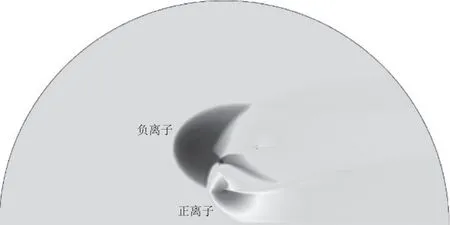
图10 左横风5 m/s 时电荷分布
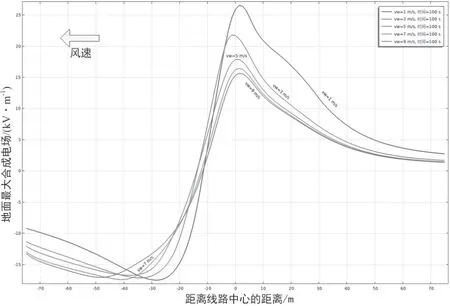
图11 方案3 右侧风不同风速下的合成电场

图12 右横风5 m/s 时电荷分布
左侧横风时(即横风从X 负半轴吹向正半轴),方案3 下近风侧合成电场随风速的增加呈现减小趋势,其中风速从1 m/s 增加到3 m/s 时,合成电场减少幅度较大;(5~9)m/s 风速下合成电场减少幅度逐渐减少。远风侧的合成电场随风速的增长呈现增大趋势;并且随着风速的增加,远风侧合成电场的高值区域范围也随之增大。造成远风侧合成电场变化趋势的原因是方案3 布置下远风侧的最上层和最下层极导线均为正极,左侧横风会加剧远风侧正极性导线的电晕效应,增加区域正离子浓度并且扩大分布范围,从而提升合成电场峰值以及其高值区域范围。
右侧横风时(即横风从X 正半轴吹向负半轴),方案3 下近风侧整体的合成电场呈现减少趋势;远风侧合成电场的峰值呈现先增大后减少趋势。由于正负极性导线电晕的原理不同,右侧横风时远风侧合成电场变化趋势的原因是:最上层和最下层负极导线电晕后因横风游离出的电子随风速偏移,且区域空气中无足够的正离子与之中和反应,从而造成末端区域合成电场呈扩散增大趋势。但由于风速的不断增大,区域内的电子浓度降低从而高风速后合成电场呈现减少趋势。
结合上述对图9、11 中合成电场在不同风速风向下的变化趋势分析,方案3 布置下直流线路合成电场峰值位置均沿风向偏移。近风侧的合成电场整体均为减小趋势,横风吹散近风侧中正离子与电子的分布状态,减弱区域离子自身产生静电场,从而减弱合成电场。远风侧合成电场的变化趋势需根据线路架构和正负极性导线布置方式来具体分析。
4.2 不对称电磁环境分析
在不同风向与风速中,方案3 特有的低值域不对称电磁环境体现出了优异的抗风性。不对称电磁环境中的低值域侧在左右横风的干扰下,合成电场整体变化幅度较小,最大9 m/s 风速时其最大值低于18 kV·m-1,满足±800 kV 直流输电线路居民区最大合成电场限值25 kV·m-1。
实际的工程建设中,在多风的走廊狭窄区域需注意自然风对特高压直流线路合成电场的影响。为了减弱横风对合成电场的影响,建议在多风区域建设特高压直流线路时,可以适当提高原杆塔的高度,增加导线离地距离;与此同时,预留出充足的走廊宽度可以解决合成电场高值区域范围扩大的情况[18]。
5 结论
本文基于双回复合型酒杯直线塔,提出改善混压双回直流输电线路电磁环境的新布置方案。案例仿真结果表明:
1)在电磁环境方面,新布置方案中方案3 的地面离子流浓度、合成电场要优于现有双回直流线路常规布局;同时方案3 布置下的高压直流线路走廊宽度更小,在输电走廊狭窄区域或临近居民区时有明显优势。
2)新方案布置较常规布局来说,其电磁环境最大的特点是不对称性,其低值域侧在峰值比较和不同风速影响下均体现出其自身的低值性与稳定性。在工程中将电磁影响较弱的低值域侧靠近居民区或电磁限制严格区域,这将减弱高压直流线路对居民生活环境的干扰并节约日益紧张的输电走廊资源。
改变直流输电极导线的空间布置方式,重构极导线电晕后正负离子的空间分布数量状态来改善电磁环境影响的研究在文中首次提出,其线路布置与杆塔设计还需更深一步的研究。

