微型涡旋压缩机轴向力曲线匹配吸力足机构优化研究*

吴 燕,蔡炯炯,闻 汇,陈 浩,陈炳拓

(浙江科技大学 自动化与电气工程学院,浙江 杭州 310023)

0 引 言

微型涡旋压缩机以设计紧凑、经久耐用、静音运行和节能性能优越而著称,因此在制冷、制造、运输和医疗保健等领域得到了广泛应用[1-2]。开发更高效、更可靠、更紧凑的微型涡旋压缩机迫在眉睫。

微型涡旋压缩机运动时,其轴向气体力随主轴转角和出口气体压力的变化而大幅度改变,存在轴向力难以控制的问题[3-4]。决定其性能的关键在于动涡盘和静涡盘之间的动态密封。因此,确保微型涡旋压缩机的轴向平衡是目前需要迫切解决的问题之一[5]。

在此背景下,众多学者针对涡旋机轴向力平衡问题提出了众多的解决方案,比如气体背压[6]、油路背压[7-8]、电磁力平衡[9-10]等。以上方案需要在直驱电机和涡旋机之间增设背压腔,或者在涡旋机动涡盘外部增设电磁结构,以实现轴向力平衡。由于微型涡旋机体积较小,结构受限制,无法采用以上方案。

DOONER M等人[11]提出了在动涡盘中加入多个永磁体的方法,该方法的应用结果表明,磁铁的数量、位置、尺寸和磁化极性对所产生的磁场的强度和分布产生了较大影响。LUO X等人[12]以此为基础提出了一种新型的永磁螺旋式涡旋式空气电机,在动涡盘和静涡盘上加工两个薄槽以容纳永磁体,该结构有效减少了涡旋机的侧面泄漏问题,进而提高了能源的利用率。KOO I H等人[13]提出了一种背压装置,即在涡旋压缩机的电机旋转轴和动涡盘上分别插入N、S交替安装的永磁体,在主轴运动过程中,利用永磁体磁极的相互吸引或排斥调节控制作用在动涡盘上的压力,令涡旋机的轴向气体力保持平衡。CAI J等人[14]提出了一种无源永磁机构,该机构包括分别安装在静涡盘和动涡盘外侧的动、静吸力环和安装在静吸力环上的永磁体,采用该结构可以使微型涡旋压缩机的轴向气体力与永磁体提供的轴向磁力相互抵消,使轴向气体力基本达到平衡状态。

根据上述分析与考虑,针对目前微型涡旋压缩机动静涡盘间轴向力平衡或平衡方法性能上的不足,笔者提出一种用于微型涡旋压缩机轴向气体分离力平衡的吸力足机构,采用吸力足机构优化以匹配微型涡旋压缩机随主轴转角变化的轴向力曲线,以解决其在轴向的气体密封问题。

首先,笔者介绍微型涡旋压缩机的气体力特性和动涡盘的数学模型;其次,选择合适的吸力足拓扑结构;然后,对永磁体位置进行研究,由此达到轴向力的最大差值;对提出的吸力足机构进一步研究,并讨论不同分块方案对目标曲线的重要性;最终,给出样机实验验证结果,总结主要研究成果。

1 微型涡旋压缩机的数学描述

1.1 动涡盘的运动轨迹

该节主要介绍微型涡旋压缩机动涡盘的数学模型[15]。动涡盘的基本形状是螺旋状,其坐标系描述如图1所示。

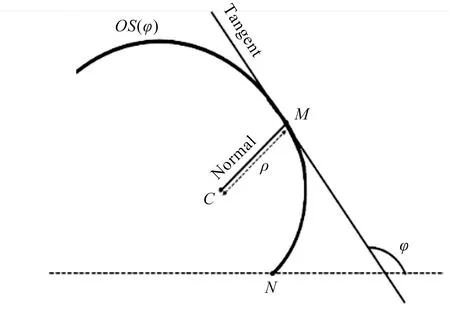
图1 动涡盘几何形状

动涡盘OS的数学描述为:

xOS=x0+(ρ0+kφ)sinφ+kcosφ-k

(1)

yOS=y0-(ρ0+kφ)cosφ+ksinφ+ρ0

(2)

式中:φ为动涡盘上一个点的切向角;ρ0为曲线半径ρ(φ)=ρ0+kφ;k为描述曲线的常数。

动涡盘的运动轨迹描述了一个半径为r的圆,涡盘在运动轨迹中的位置由角度θ得到。

根据式(1)、式(2)可得到OS(φ)=OS(φ)+D(θ),表达如下:

D(θ)=r(sinθ,-cosθ)

(3)

xOS(φ,θ)=x0+(ρ0+kφ)sinφ+kcosφ-k+rsinθ

(4)

yOS(φ,θ)=y0+(ρ0+kφ)cosφ+ksinφ-ρ0+rcosθ

(5)

1.2 轴向气体力特征分析

微型压缩涡旋机平动时,动涡盘会受到轴向力、切向力及径向力。在外部增设不同机构,为动涡盘提供轴向平衡力Fb,可有效平衡活动卷轴上的轴向气体力Fa。

动涡盘轴向受力情况如图2所示。

图2 动涡盘轴向受力

根据文献[16],涡旋压缩机中的轴向气体分离力表达式如下:

Fa(θ)=

(6)

式中:ps为吸气压力;P为渐开线节距;A1为中心压缩腔轴向气体力的作用面积;N为渐开线的圈数;ρi为第i个压缩腔的压力比。

此外,在涡旋机平动过程中,各腔室的容积和压力都会发生变化,因此,轴向气体力是主轴转角θ的函数。

将涡旋机的具体参数代入以上公式,即得到轴向气体力Fa随θ变化的关系,即气体作用力随转角变化图,如图3所示。

图3 气体作用力随转角变化图

图3中,轴向气体力Fa随主轴转角变化而大幅度改变,变化周期为2π,在主轴转角为270°时达最大值50 N,在主轴转角为0°时达最小值31.8 N,平均值为38.904 N,极差为18.2 N。

2 吸力足机构拓扑分析

2.1 拓扑结构

由于微型涡旋机结构简单紧凑,无法增设背压腔。故笔者采用一种轴向力控制机构,将其置于动涡盘背部和涡旋腔。该机构采用永磁体对固定在动涡盘上的动环产生吸力,以平衡压缩腔内产生的轴向气体力。

为了增大吸力足的面积,在微型涡旋机内部机构中采用类腰圆形状的吸力足,如图4所示。

图4 吸力足永磁机构摆放位置

进一步,笔者给出微型涡旋机初始设计参数及其数值,作为后续研究的初始约束条件,如表1所示。

表1 微型涡旋压缩机初始设计参数

吸力足机构剖面图中标注的设计参数如图5所示。

图5 吸力足机构设计参数标注图

2.2 结构选择

吸力足永磁机构采用2n永磁体,轴向充磁,相邻永磁体极性相反。吸力足和永磁体的体积相同,分别在动环和静环上均匀分布[17-18]。

文献[19]提出,永磁体的大小决定轴向磁通电机转子盘之间的拉力大小,故其在吸力足机构中的永磁体用量会对轴向力产生较大影响。

为选择合适的拓扑结构,在保持吸力足和永磁体的用量相同的前提下,笔者通过改变两者的数量,提出了3种不同的永磁机构,吸力足和永磁体个数分别为4、6、8。

不同个数吸力足永磁机构如图6所示。

图6 不同个数吸力足永磁机构

微型涡旋压缩机做循环运动。其磁场分布的变化趋势和广义力在每个循环中周期性重复。吸力足机构的磁场分布变化取决于动环和吸力足的相对位置,而两者相对位置由动涡盘的瞬时位置决定。

根据仿真结果,吸力足机构受到的轴向力如图7所示。

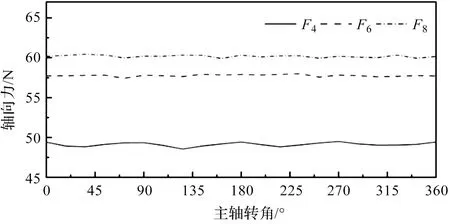
图7 不同个数吸力足机构轴向力对比

笔者对于吸力足机构的每个位置进行磁场分析,采用JMAG进行磁场分布模拟,其运动位置可通过代入式(3)、式(4)中经计算得到。

不同个数吸力足机构磁密及矢量图结果如图8所示。

图8 不同个数吸力足机构磁密及矢量图

3种不同的吸力机构的永磁体和硅钢片用量相同。永磁体和吸力足均匀分布,轴向力曲线水平保持不变。F8平均值相较于F4提升了22.45%,相较于F6提升了4.34%。

根据磁密和矢量图分析,分块个数减少,机构趋于磁饱和状态。其总磁动势不变,永磁体个数增加,磁阻减小,磁饱和减小。但构成磁路增加,磁力变大。

根据上述分析可知,机构总体积不变,应选择能提供较大轴向力的方案;但6块与8块吸力足机构提供的轴向力大小接近,考虑实际制作中8块结构过于紧凑的问题,笔者选择6块吸力足机构为后续优化基础。

3 永磁体位置优化研究

笔者提出的吸力足机构由永磁体提供轴向磁力。轴向磁力与微型涡旋压缩机的轴向气体力相互抵消,达到平衡。轴向力的大小与吸力足在永磁体上的投影面积有关。为匹配目标轴向力曲线,可改变永磁体的安放位置以实现轴向力变化最大的目标。

当任意时刻永磁体提供的轴向力大于Fa不同主轴转角下的轴向气体力时,则判定该轴向力曲线满足优化要求,其表达式如下:

Fm(θ)-Fa(θ)≥0 ∀θ

(7)

在满足要求的基础上,优化曲线Fm与Fa越接近,代表吸力足机构平衡性能越好。因此,将一个周期内不同角度下Fm与Fa的最大力的差值和它们的积分差分别定义如下:

Δmax=Max(Fm(θ)-Fa(θ))

(8)

(9)

最大误差和积分差越小,说明优化曲线与目标曲线越接近。

3.1 优化方法与目标

笔者采用遗传算法对吸力足机构进行全局优化。比较每个目标函数,以最小化或最大化每个解决方案;并使用提取的层次关系,搜索其帕累托最优解[20]。

在遗传算法设置中,不改变永磁体的材料属性以及体积,仅改变永磁体的相对位置。设置变量永磁体的横坐标为Xi,旋转角度为Ai(i为对应的各个永磁体)。其中,Xi范围为-2 mm～0 mm,Ai范围为0°～33.6°。

永磁体位置目标范围如表2所示。

表2 永磁体位置优化目标

3.2 优化结果分析

永磁体位置遗传算法优化结果散点图如图9所示。

图9 永磁体位置遗传算法优化历程

图9中,横轴为优化曲线与目标曲线的积分差,纵轴为优化曲线与目标曲线在不同角度下最大的力的差值;永磁体的位置优化仅考虑轴向力的变化趋势,故积分差和轴向力差值均应达到最大值。

由此,可选择实心点为最佳的永磁体安装位置,如图10所示。

图10 永磁体最优安装位置

轴向力示意图为图11中的Hsf-2 mm曲线。后续优化均以此为基础。

图11 吸力足高度变化图

4 吸力足分块方案研究

优化后的永磁体位置的吸力足机构的轴向力远大于目标轴向力。吸力足是该机构的重要组成部分。

为了更好匹配目标轴向力,笔者对该机构的吸力足高度行单参数进行分析,各个吸力足同步变化。

吸力足高度变化图如图11所示。

图11中,吸力足高度减小,气隙增加,轴向力减小。

4.1 吸力足分块方式

根据吸力足的高度分析,可以得出吸力足的高度变化轴向力的大小和趋势互相产生影响。由此,可对动环上的吸力足分块,产生出4种分块方案,如图12所示。

图12 4种不同的永磁体分块方案

可通过改变各个吸力足的高度,以此来匹配动涡盘平动过程中随主轴角度变换的轴向力曲线。

其中方案A不分块,方案B可径向切割为2块,方案C可周向切割,方案D将吸力足均分成4块。

4.2 优化方法与目标

吸力足高度仍需要采用遗传算法进行优化。笔者将各个的吸力足高度用作设计变量,变量范围为0 mm～2 mm。

根据动涡盘的运动特征,为提高算法计算效率,笔者仅选定目标曲线峰值附近5个点为优化目标。

为防止永磁体提供的吸力小于微型涡旋机自身的轴向气体力导致漏气的情况,可增大优化目标范围,令永磁体提供的轴向吸力始终大于目标力。

分块吸力足优化目标范围如表3所示。

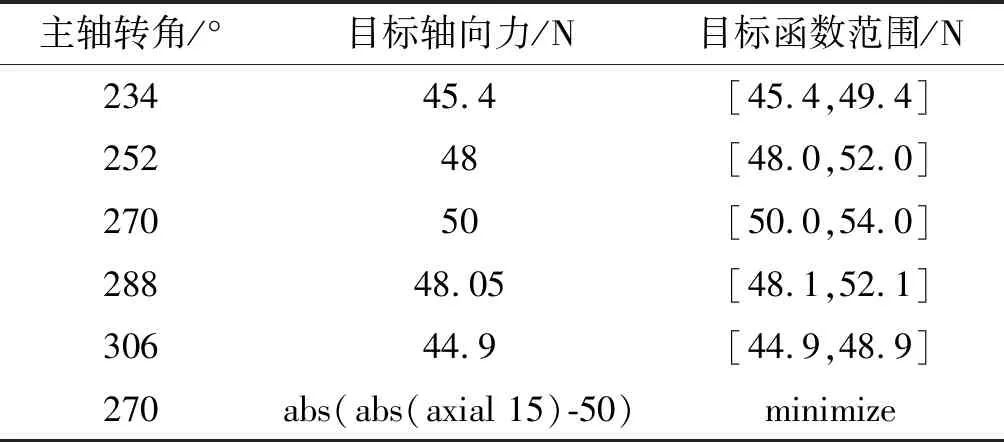
表3 分块吸力足优化目标

4.3 优化结果分析

笔者针对A、B、C、D,4个方案寻到的优化结果绘制二维散点图,如图13所示。

图13 吸力足分块遗传算法优化历程

从图13中可以看出:不分块的方案A满足要求的结果较分散,径向分块的方案B满足结果虽然相较于A多,但其总体分布仍与A相似;

方案C和D满足的结果均分布在坐标轴前端,且方案D更加密集。

不同分块方法的轴向力曲线如图14所示。

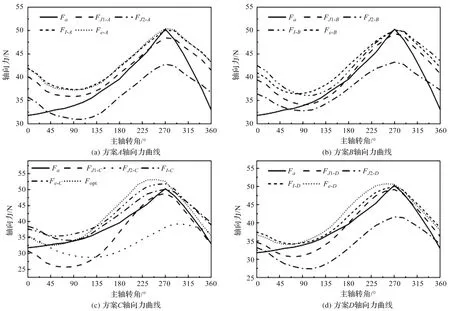
图14 不同分块方法的轴向力曲线

图13中的散点图以所寻曲线和目标曲线的积分差为横轴,以在不同主轴转角的所寻曲线和目标曲线的最大误差为纵轴;十字点代表所有case的结果,圆点代表满足在目标曲线上方的情况;选取圆点最外侧的结果,得到帕累托前沿,如三角点所示;选取最大误差最小和积分差最小的case绘制曲线,如图14中Fe,FI所示。

为有效对比各个不同case曲线的优劣程度,笔者在图14中增加了以下不同方案的轴向力曲线,分别为JMAG自动寻优找到的最佳方案FJ1和JMAG自动寻优的中间值方案FJ2;将FJ2与其他轴向力曲线对比,轴向力明显优化,与目标曲线的匹配程度上升;JMAG自动寻优的曲线FJ1的匹配最高,在某些时刻,其轴向力小于目标值,有漏气风险。

4个方案的优化结果趋势与目标轴向力基本一致。当主轴转角θ为0°和360°时,方案A和B轴向力明显大于方案C和D,该位置方案C较方案A轴向力降低了10.01%;方案D较方案A轴向力降低了12.29%;方案D明显优于其他3个方案。

4.4 优化结果分析对比

把4.1中4个分块方案的最优结果代入计算Cost值,可得到不同分块方案得到的Cost结果,如图15所示。

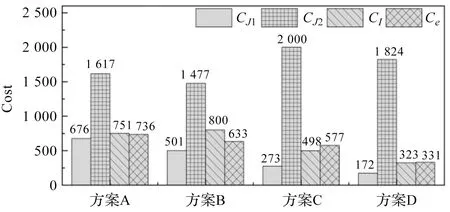
图15 不同分块方案得到的Cost结果

在图15的同一分块方案中,能够明显发现JMAG自动寻优的最佳case的Cost值CJ1低于其他案例。若仅根据Cost选取最佳方案,结合点线图分析,微型涡旋压缩机会面临漏气的风险。

比较方案A和方案B,虽然B的永磁体块数多于A,但Cost值基本一致;方案B和方案C吸力足总块数相同,区别在于方案B采用径向切割,方案C采用周向切割;周向切割的Cost值小于径向切割的Cost值;比较方案D与其他方案,发现吸力足分块数越多,轴向力匹配程度越高,Cost值越小。

4个方案的实质性提升可归结于两大因素:1)分块个数增加,不同位置的吸力足高度可变性增加;2)动涡盘在永磁体上方平动,周向切割的永磁体分块方式与其运动方向基本吻合。故方案C和D的轴向力曲线与目标曲线匹配程度高。

综上所述,在吸力足总块数相同的前提下,选择周向切割往往优于径向切割;吸力足分割块数越多,轴向力匹配程度越高,但考虑实际制作难度和多分块减缓仿真速度,可选择周向切割、分割块数较少的方案C作为最终方案。

为减少制作过程中的复杂性,固定对轴向力趋势影响较小的吸力足高度,采用箱线图对每个吸力足的高度进行敏感性分析,对满足要求的优化结果的吸力足高度数据进行敏感性分析,并将方案C的帕累托前沿中的3个点在箱体图中标注,得到方案C吸力足高度敏感性分析结果,如图16所示。

图16 方案C吸力足高度敏感性分析

图16中,箱体的高度越高,代表该吸力足高度的敏感性越低;可将其高度固定在箱体范围内的任意位置。

结合箱线图箱体高度和中位线以及帕累托前沿3个点的分布,可确定不同位置的吸力足高度。

固定参数的吸力足机构三维图如图17所示。

图17 固定参数的吸力足机构三维图

最终优化后的轴向力如图14中Fopt曲线所示。

5 实验及结果分析

为验证有限元仿真结果的准确性,笔者制作了初始设计和最终优化设计两个原型,并采用实验平台对两者进行测试。

实验测试平台如图18所示。

图18 实验测试平台

吸力足机构模型如图19所示。

图19 吸力足机构模型

吸力足机构样机参数如表4所示。

表4 吸力足机构样机参数

最终优化设计的分块吸力足高度与图17保持一致。两者动环和静环的几何尺寸均相同,但它们在永磁体的位置分布和吸力足高度上有所不同。

实验中因为难以确保0.2 mm的精确气隙,故笔者在气隙为1 mm时对其进行测试。其中,为方便加工制造,永磁体的形状与前述研究略有所不同,采用环形结构。

该平台由吸力足模块、光学工作台、微调滑块、夹具、三维力传感器、变送器和电源组成。动环和静环分别被固定在顶端的夹具和力传感器上。3D力传感器与微调平台相连接,由此可控制静环的相对运动。力传感器连接RTU-BOX进行数据采集。

有限元仿真和实验结果对比如图20所示(其中,实验一为初始设计方案,实验二为最终优化设计方案)。

图20 有限元仿真和实验结果对比

图20中,实验一中有限元仿真与实验测试结果的最大误差仅为3.7%,具有良好的一致性;实验二中的最大误差为6.2%,但其有效预测了270°和108°的最大和最小轴向力。

实验二的较大误差可能由于制造和组装难度较大造成。实验误差原因分析如下:1)实验装置气隙由筛尺固定,可能存在一定误差;2)永磁体和吸力足均采用胶水与动环和静环固定。

另外,人工固定的永磁体和吸力环位置与仿真存在误差;在动环的运动过程中,铁芯可能超出静环外围,导致轴向力减小。

6 结束语

笔者提出了一种微型涡旋压缩机轴向力曲线匹配吸力足优化机构,分别对吸力足结构中的永磁体和吸力足进行了优化分析;最后,通过实验验证了有限元仿真结果的准确性。

研究结论如下:

1)采用遗传算法优化永磁体在静涡盘上的安放位置以达成轴向力变化最大的目标,优化后的轴向力最大值提升了27.56%,轴向力的大小与永磁体在静环的相对位置有关;

2)4种分块方案将每块吸力足高度参数化,采用遗传算法优化,使永磁体提供的轴向平衡力能够匹配涡旋机轴向气体力;周向切割的积分差相较于径向切割方案减小了42.91%,该方案优于径向切割,且吸力足分块数越多,平衡性能更佳;

3)对最终方案的吸力足高度进行了敏感性分析;固定敏感性低的参数,降低实际制作的难度,对结果进行了实验验证,最大误差仅为6.2%,较大程度解决了轴向气体力的不平衡问题。

在后续的研究中,笔者将进一步考虑压缩机中存在的径向力和切向力,以实现微型涡旋压缩机良好的轴向密封功能,有助于提高其工作效率。