调制光学参量放大器对双机械振子量子纠缠与压缩的影响

杜宏杰，郭金良

（天津师范大学物理与材料科学学院，天津 300387）

腔光力系统[1]是研究量子力学特性由介观尺度到宏观尺度的一种方法，其主要研究对象是机械振子与光腔间可控的辐射压力相互作用.近年来，凭借潜在的应用价值和前沿的研究成果，腔光力系统成为应用工程科学和基础研究科学的有力平台.此外，量子纠缠作为量子物理学的基石，在量子理论基础和量子信息处理等潜在应用中具有重要的作用[2].宏观纠缠不仅可以帮助科研人员阐明宏观自由度由经典世界到量子体系的转变[3-5]，而且在连续变量系统中也是重要的资源[6-7].因此，制备宏观纠缠具有重要的意义.目前，已有研究在各种光学机械装置中提出许多方案来产生量子纠缠，如通过光（微波）场与一个可动镜间的直接辐射-压力耦合产生光（微波）-机械纠缠[8]，但该光-机械纠缠容易被系统的热噪声破坏.Mari 和Eisert[9-10]通过将周期性调制驱动场引入经典光机系统极大地增强了光机纠缠，但受限于系统的稳定性，纠缠强度仍无法超过1 ebits 的稳态纠缠极限.此外，还有一种宏观纠缠是2 个机械振子间的机械-机械纠缠，由于早期基于直接辐射-压力相互作用方案制备所得机械-机械纠缠较脆弱[11-12]，研究人员在光机系统中应用了如直接机械耦合、压缩真空光输入、单光子强耦合或周期调制泵浦等技术，但纠缠的增强量并不显著.近年来，研究人员提出许多使2 个力学振子产生纠缠的方案，如利用纠缠交换[13]、使用压缩光驱动双腔[14]以及注入一对纠缠光束到独立的2 个光学腔[15].Joshi 等[16]利用光纤对2 个不同的Fabry-Perot 腔进行耦合，但所得力学纠缠很小且受限于很低的热温度.Chen 等[17]利用周期性调制驱动，使由2 个力学模组成的光学腔压缩复合模产生了较强的力学纠缠.实现宏观振子的压缩对精密测量的科学研究非常重要.近年来，研究人员通过各种非线性方案实现了机械振子的稳态压缩，如机械振子固有的非线性[18]以及系统中内在的非线性耦合[19]或非线性介质[20]等.Lu 等[21]利用非线性机械振子在腔光力系统中成功引入机械非线性，将系统动力学线性化，构造有效哈密顿量制备机械压缩.此外，热库方案通过不同频率的2 个激光场驱动系统将哈密顿量线性化设计为非对称的Rabi 型相互作用，实现了机械振子的稳态强压缩[22].

非线性介质与光机系统的组合效应使得强压缩的制备变得容易，并取得了实质性进展，如二阶非线性简并光学参量放大器（OPA）在产生压缩光方面效果良好[23].实验表明，放置在腔内部的OPA 可以极大地增强机械冷却，产生强的机械压缩，并将单光子的光机耦合强度提升到强耦合状态，提高检测光机位置的精度[24-27].Hu 等[28]通过调制OPA 增强机械纠缠，并将周期调制腔驱动和OPA 的参数驱动联合，在腔光机系统中实现了双重机械压缩[29]，但有关2 个机械振子间宏观机械-机械纠缠的研究相对较少.

基于这种联合驱动效应的良好效果，本研究主要讨论了在施加OPA 的腔光力系统中，OPA 对双机械振子量子纠缠和压缩的影响.通过对系统相关参数的讨论以及求解系统稳态的动力学演化，分析调制OPA对力学纠缠和压缩的影响.

1 模型与哈密顿量

图1 为由2 个机械振子和简并的光学参量放大器（OPA）组成的复合腔光力系统.

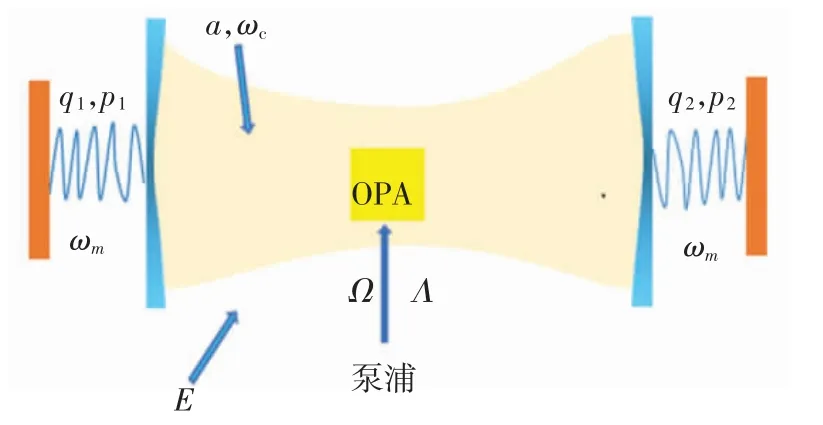
图1 腔光力系统示意图Fig.1 Schematic diagram of the cavity photomechanical system

图1 系统中，2 个机械振子通过辐射压力同时与1 个光腔耦合.机械振子的质量为m，频率为ωm，耗散为γm，频率为ωc、衰减率为κ 的光腔被频率为ωl、强度为E 的激光场驱动.此外，置于光腔中的OPA 被频率为2ωp的泵浦激光驱动，其产生的参量增益为Λeiθ，该增益由泵浦激光的强度和相位共同决定.以驱动激光频率ωl为旋转框架，系统哈密顿量可以写为（h¯=1）

式（1）中：△0=ωc-ωl和Ω =2ωp-2ωl分别为光腔和简并光子相对于驱动激光的失谐量；a 和a†为腔模的产生和湮灭算符；qj和pj分别为2 个振子的坐标和动量算符，满足对易关系[qj，pj]=ih¯；g 为由辐射压力引起的光腔和机械振子间的单光子光力耦合强度.

考虑到系统的耗散和涨落，式（1）中复合光力系统的动力学可用一组朗之万方程（QLEs）描述，δO/δt=i[H，O]+N-Hdiss，其中N 为量子噪声算符，Hdiss描述系统的耗散，O=pj，qj，a 为表征系统的算符，

式（2）中：ain（t）为平均值为0 的腔场输入噪声算符，满足关联函数〈〉= δ（t - t′）[19]；ξj（t）为作用于机械振子的热噪声算符；在高品质机械振子极限下Q≡ωm/γm>>1，满足马尔可夫近似，即〈ξj（t）ξj（t′）+ξj（t′）ξj（t）〉/2 = γm（2nm+ 1）δ（t - t′）[30]，且nm=[exp（h¯ωm/kBT）-1]-1表示机械振子的平均热激发数；kB为玻尔兹曼常数；T 为环境的温度.

当腔场受到强激光驱动时，对朗之万方程组（式（2））采用标准的线性化技术进行处理，将每个海森堡算符重写为其稳态平均值与微小涨落的和，即O=〈O（t）〉+δO，并通过对腔场进行强激光驱动使腔内光子数〈a（t）〉满足〈a（t）〉1.式（2）中，δp1、δp2和δa 为围绕着稳态平均值的小波动算子，在这种强激光驱动的情况下，可以安全地忽略非线性项.因此，式（2）可以通过忽略波动中高于一阶项的项被线性化.关于经典平均值〈O（t）〉的详细讨论在下面章节中，同时量子涨落部分δO 的线性化朗之万方程可以表示为

式（3）中：△1（t）=△0-g〈q1（t）〉-g〈q2（t）〉为由机械运动产生的腔场的有效失谐；式（3）中已经忽略掉非线性项[31]，因此系统的有效哈密顿量可以表示为

2 系统的经典动力学及其解析解计算

量子涨落部分（式（3））的演化与经典动力学〈O（t）〉有关，为研究系统的动力学演化，首先要求解经典平均值.本文中相同频率的2 个机械振子同时与1 个腔场耦合，因此认为其经典动力学是相同的，即〈q1（t）〉=〈q2（t）〉=〈q（t）〉，〈p1（t）〉=〈p2（t）〉=〈p（t）〉，经典平均值的演化可以通过以下非线性微分方程描述

虽然精确求解式（5）中的平均值非常困难，但如果系统远离光力非稳态和多稳态时，可以用微扰的方式来处理光力耦合[8].在弱光力耦合强度为g 和频率失谐为Ω 的条件下，将近似解析解展开为双重幂级数的形式[32-33]，即

将式（6）代入式（5）可得与时间无关的系数On，j（O=p，q，a，j ＝0）

当j≥0 时，

图2 为腔模平均值〈a（t）〉实部和虚部的时间演化关系及相空间轨迹图，图2（a）为通过数值解（蓝色实线）和解析解（红色虚线）所得腔模平均值〈a（t）〉的实部和虚部随时间的演化图像，其中时间单位τ ＝2π/Ω，所选系统参数为（单位为ωm）κ ＝0.1，Δ0＝1.06，g ＝4×10-6，γm＝10-6，E ＝1.4×104，nm＝0，Λ ＝0.3κ，θ ＝0，Ω ＝2，截断式（8）到|n|≤1 和j≤8.由图2（a）可知，在长时极限下，〈a（t）〉的演化周期与调制周期τ ＝2π/Ω 相同，且解析结果（红色虚线）与数值模拟结果（蓝色实线）非常吻合，说明用微扰的方法求解解析解是可行的.图2（b）为〈a（t）〉的相空间演化轨迹，其中红线和蓝线分别表示近似解析解和数值解.数值解给出的轨迹（蓝线）在数百个调制周期后收敛为与分析结果（红线）一致的极限环.

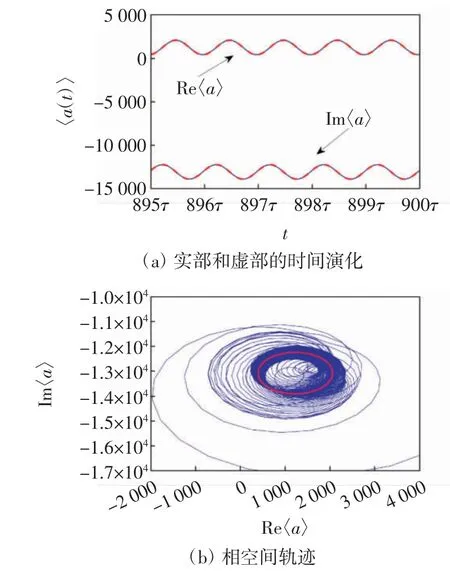
图2 腔模平均值〈a（t）〉实部和虚部的时间演化关系及相空间轨迹图Fig.2 Time-evolution relations and phase-space trajectories of the real and imaginary parts of the mean value〈a（t）〉of a cavity mould

图3 为机械模在不同时间间隔内的相空间演化轨迹，蓝色实线和红色虚线分别为数值模拟结果和解析结果，所选参数与图2 相同.

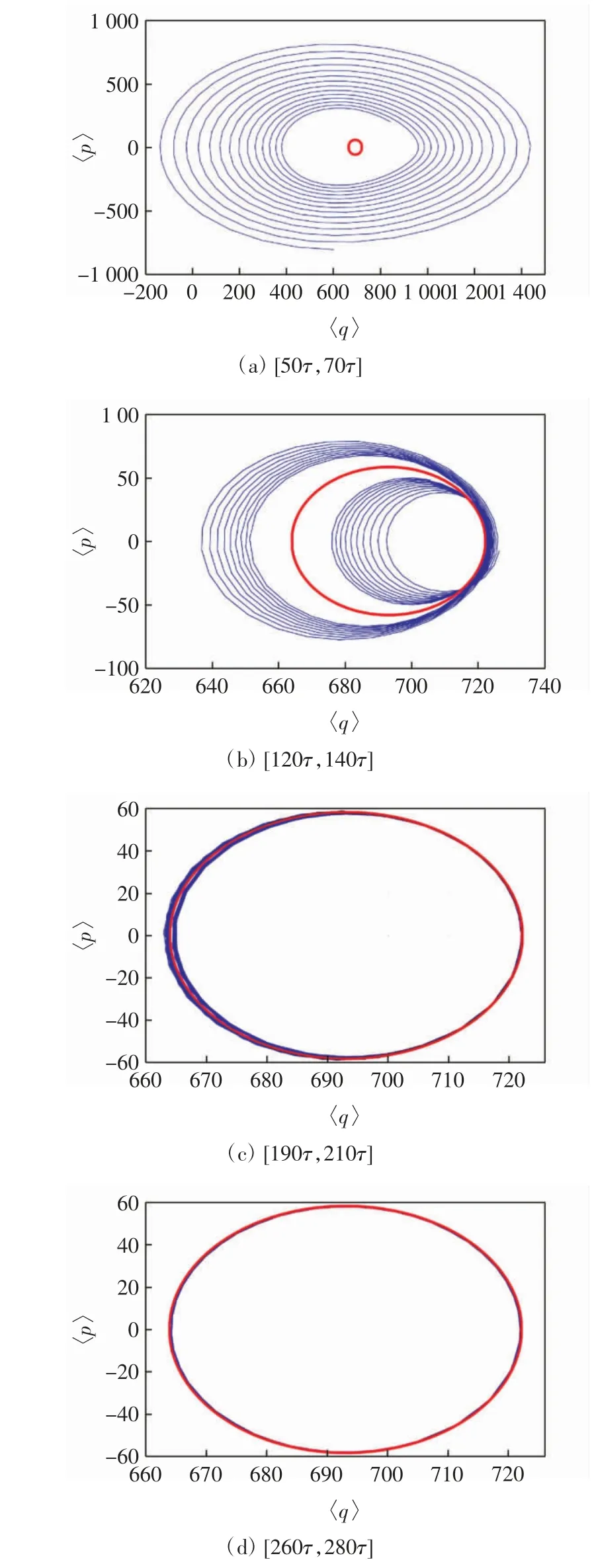
图3 不同时间间隔力学模的经典平均值〈q（t）〉和〈p（t）〉的相空间演化轨迹Fig.3 Phase space evolution trajectories of the classical mean〈q（t）〉and〈p（t）〉for the mechanical modes for different time intervals

由图3 可知，由于γm=κ，经典平均〈q（t）〉和〈p（t）〉在相空间中的演化需要260τ～280τ 才能演化到解析结果所预测的极限圆.

图4 为系统达到稳定时腔模平均值的模在时间间隔为895τ～900τ 内的动力学演化关系，所选参数与图2 相同.

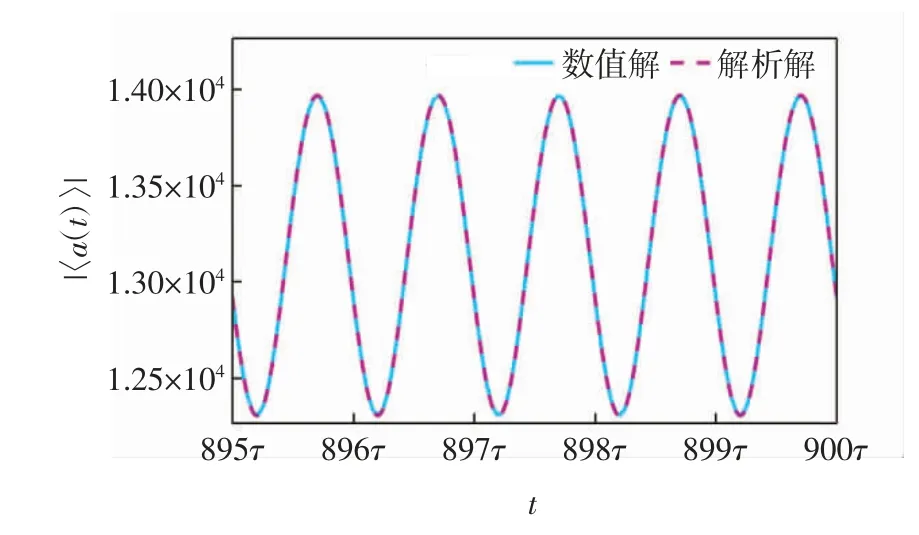
图4 系统达到稳定时腔模平均值的动力学演化关系图Fig.4 Kinetic evolution of the cavity mode average value when the system reaches stability

图4 中，〈a（t）〉的解析解（虚线）与数值解（实线）拟合较好，进一步验证了微扰近似解析解的准确性.

3 力学纠缠与压缩度量

为在数值上验证第2 节中系统经典动力学的定性讨论，本研究通过负对数值来度量力学纠缠.首先，引入腔模的振幅和相位涨落算符δX=（δa+δa）†/和δY = （iδa - δa†）/及其相应的噪声算符δXin=则式（3）可以表示为u˙（t）=M（t）u（t）+n（t），其中u（t）T=（δq1，δp1，δq2，δp2，δX，δY），矩阵

式（9）中：n（t）T= [0，ξ（1t），ξ（2t），δXi（nt），δYin（t）]，R1=-κ+2Λcos（Ωt-θ），R2=△-2Λsin（Ωtθ），R3=△-2Λsin（Ωt-θ），R4=-κ-2Λcos（Ωt-θ），G（Xt）和G（Yt）分别为有效耦合G（t）=g〈a（t）〉的实部和虚部.为了确保系统的稳定性，Routh-Hurwitz准则要求M（t）本征值的实部在任何时候都必须小于0[10].后文中所选参数均已验证满足稳定性条件，系统最终会趋于一个稳定的高斯态.6 × 6 协方差矩阵V（t）可以描述这个高斯型系统的特性，矩阵元Vi，j=〈ui（t）uj（t）+uj（t）ui（t）〉/2.结合式（9）有

式（10）中：D=diag[0，-γm（2nm+1），0，-γm（2nm+1），κ，κ]为噪声关联矩阵.V˙（t）可以描述整个系统的动力学演化，同时通过数值模拟可以直接求解式（10）.系统经过一段时间的演化后，经典动力学具有一个稳定的周期时，可用负对数值EN度量双模高斯态中的两体纠缠.提取协方差矩阵V（t）的前四行和前四列，即可组成有关2 个力学模式的协方差矩阵

式（11）中：A、B 和C 分别为2×2 的子矩阵，负对数值

式（12）中

式（13）中：Σ（V）=detA+detB-2detC，如EN>0，即η<1/2，说明2 个力学振子间存在纠缠.

协方差矩阵V（t）的第1 个对角矩阵元V11（t）=〈δq（t）2〉和第2 个对角矩阵元V22（t）=〈δp（t）2〉分别表示力学振子的位移和动量涨落的方差.系统达到稳定时，如满足〈δq（t）2〉<1/2 或〈δp（t）2〉>1/2，则对应的坐标或动量分量被压缩.力学压缩的强度可用dB 为单位来度量，对应的计算方式为-log10[〈δO（t）2〉/〈δO（t）2〉vac]（O=p 或q）和〈δq（t）2〉vac=〈δp（t）2〉vac=1/2 分别表示力学模真空态的位移和动量方差.

4 结果与讨论

4.1 机械纠缠

通过对负对数值EN进行数值模拟，分析OPA 对机械纠缠的影响.首先，给出OPA 的相位对机械纠缠EN的影响.图5 为不同相位时，EN随时间t 的变化图像.图5 中，E ＝6×104，其他参数与图2 相同.由图5可以看出，系统经过一段时间的演化后，机械纠缠与经典动力学一样最终以周期τ 随时间变化.因此，下文只考虑相位θ ＝0 的情况.

图5 力学纠缠EN 在不同的参量相位下随时间t 的演化关系Fig.5 Evolution of mechanical entanglement EN with time t for different parametric phases

由于机械纠缠的演化具有周期性，可以通过一个周期内EN的最大值来量化机械纠缠的大小[34].即

图6 为机械纠缠的最大值EN，max随OPA 失谐量Ω/ωm的变化关系，图6 中最佳失谐Ωopt/ωm＝2.008，其他参数与图5 相同.

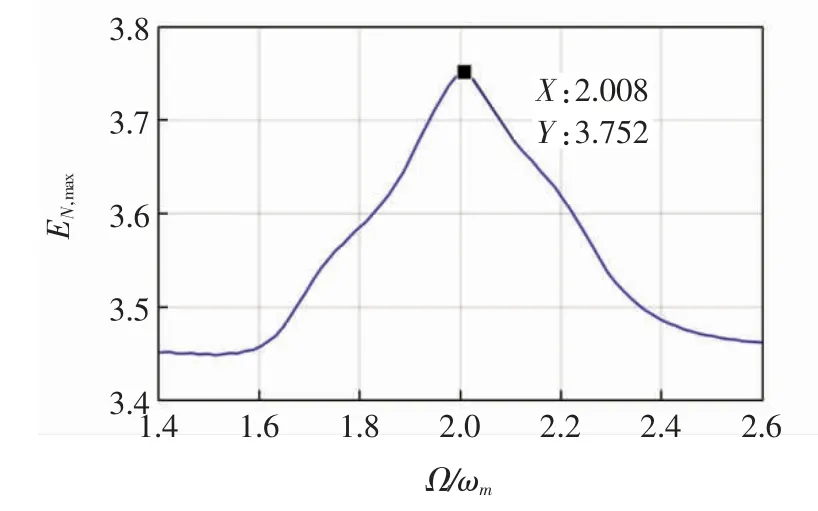
图6 最大机械纠缠EN，max 随OPA 失谐量Ω/ωm 的变化关系Fig.6 Variation of maximum mechanical entanglement EN，max with OPA detuning Ω/ωm

由图6 可以看出，存在最优的调制频率Ωopt/ωm＝2.008 使EN，max最大，且由于光力耦合对光腔有效失谐△（t）的轻微修正，最优调制频率Ωopt接近但略大于2ωm，这正是前文讨论中选取Ω ＝2ωm的原因.

为研究有限热温度和OPA 对机械纠缠的影响，图7 为不同热声子数条件下以及OPA 的增益Λ 在有限温度下机械纠缠随时间的演化关系图，图7 中参数与图5 相同.图7（a）为不同热声子数nm＝0（蓝色）和nm＝0.2（红色）条件下机械纠缠随时间的演化.图7（b）为OPA 的增益Λ ＝0（蓝色）和Λ ＝0.3κ（红色）对有限温度下机械纠缠演化的影响.

图7 系统达到稳定时机械纠缠EN 随时间的演化关系Fig.7 Evolution of mechanical entanglement EN with time as the system reaches stability

由图7（a）可以看出，随着热声子数的增加，环境温度的升高抑制了系统的量子效应，导致系统机械纠缠的值降低.由图7（b）可以看出，与Λ ＝0 的情况相比较，随着Λ 的增大，机械纠缠被增强，这表明在OPA 的辅助下机械纠缠可以在一个相对较大的热声子数条件下存在，即机械纠缠对热噪声具有很强的鲁棒性.

4.2 压缩效应

最后，通过计算动量涨落的方差〈δp2〉研究调制OPA 对机械压缩的影响.根据海森堡测不准原理，当〈δp2〉<1/2 时，机械振子的动量获得压缩.图8 为OPA的增益Λ 取不同值时，〈δp2〉随时间的变化，图8 中其他参数与图5 相同.

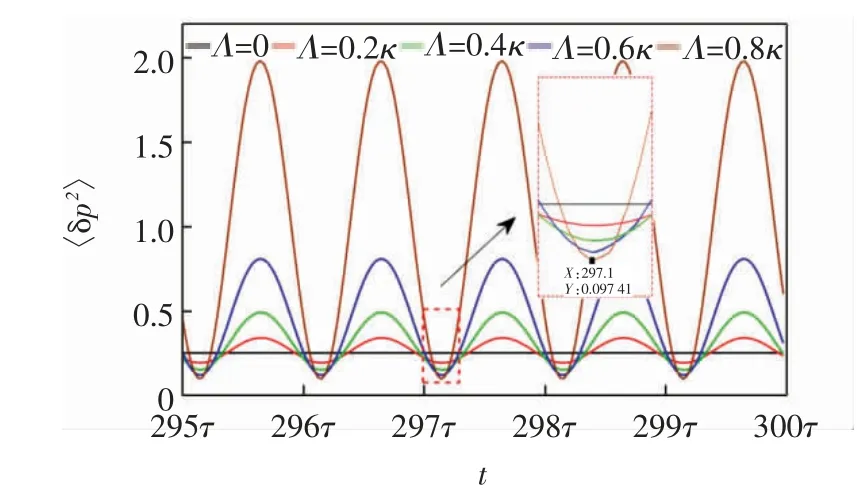
图8 力学涨落的方差〈δp2〉随时间的变化关系Fig.8 Variance of the force rise and fall〈δp2〉versus time

由图8 可知，相比于Λ=0 的情况，随着Λ 的增大，机械振子的动量压缩被周期性加强.当Λ=0.8κ 时，〈δp2〉最小值达到7.12 dB（对应的动量方差〈δp2〉min=0.097 41），远大于一般的机械压缩，可以认为是强压缩[35-37]，这说明机械压缩可以在调制OPA 的辅助下增强.

图9 为热声子数nm对机械压缩的影响，图9 中其他参数与图5 相同.

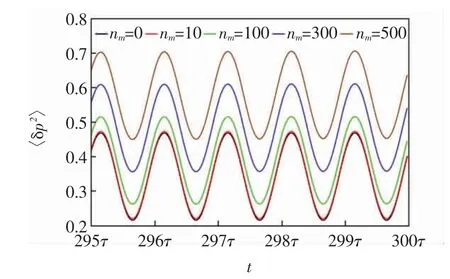
图9 力学涨落的方差〈δp2〉随时间的变化关系Fig.9 Varianceofthemechanicalriseandfall〈δp2〉versustime

由图9 可以看出，〈δp2〉的最小值随热声子数nm的增加略有增加，即使nm增大到500，仍可实现机械压缩，因此系统产生的机械压缩对环境温度具有很强的鲁棒性.

以上讨论的机械压缩是在边带可分辨的条件下，即ωm≫κ.而标准的腔光力系统很难在实验中获得高品质的腔，并满足可分辨边带条件，因此讨论在边带不可分辨条件（κ>ωm）下是否可以实现机械压缩非常必要.

图10 给出边带不可分辨条件（κ>ωm）下，力学涨落的方差〈δp2〉随时间的变化关系，图10 中其他参数与图5 相同.

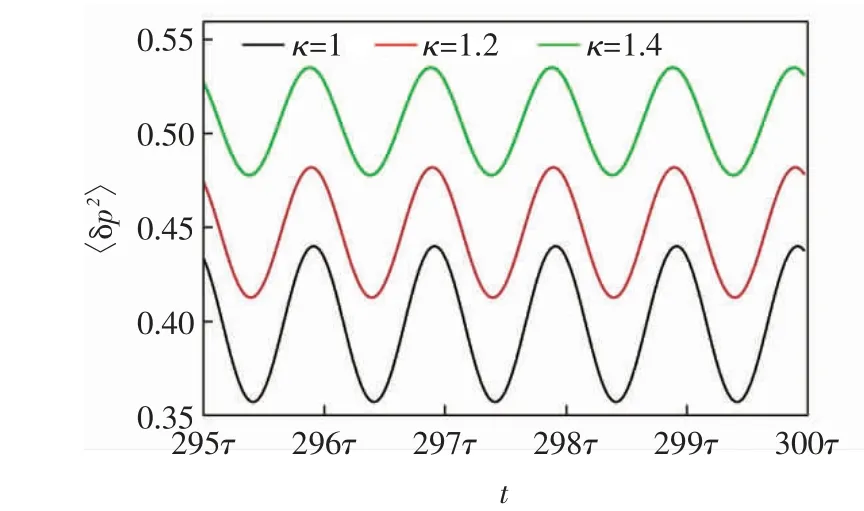
图10 边带不可分辨条件（κ>ωm）下力学涨落的方差〈δp2〉随时间的变化关系Fig.10 Variance of mechanical rise and fall〈δp2〉versus time under indistinguishable conditions（κ>ωm）in the sidebands

由图10 可以看出，机械压缩的程度随着腔耗散率κ 的增加明显减弱，但仍可以在边带不可分辨条件（κ>ωm）下实现机械压缩.因此，在调制OPA 的辅助下，对于耗散较大（κ>ωm）的光力系统也可以实现机械压缩.

5 结论

本文研究了与同一光腔耦合的2 个机械振子间的量子纠缠和机械压缩.通过数值和解析求解经典平均值的运动方程，分析了系统动力学的演化.计算结果表明，调制光学参量放大器对双机械振子腔光力系统中的量子纠缠和机械压缩效应的影响均有良好的效果：

（1）对系统施加调制OPA，通过调节OPA 相对于驱动激光的失谐量可以增强2 个机械振子间的纠缠.

（2）在调制OPA 的辅助下，机械振子间的纠缠对系统的热噪声表现出很强的鲁棒性.

（3）在边带可分辨条件下，通过调制OPA 的作用可以实现较强的机械压缩，且对于边带不可分辨的情况，利用调制OPA 也可产生机械压缩.因此调制OPA对于系统实现机械压缩具有关键的作用.