结合双流形映射的不完备多标签学习

许智磊,黄睿

(上海大学通信与信息工程学院,上海 200444)

0 引言

传统的单标签学习在实际应用中已无法有效应对复杂且多语义的海量数据。为处理这种多语义数据,多标签学习应运而生。与一个实例只属于一个类别的单标签学习不同,多标签学习认为一个实例可以同时具有多个类别标签。近年来,多标签学习受到研究者的重视,并被广泛应用于情感分类[1]、音乐检索[2]、文本分类[3]、图像/视频标注[4-5]等领域。

多标签学习通常被认为是单标签学习的扩展。根据单标签学习思想进行多标签学习,算法可以分为两类[6]:问题转换和算法适应。第一类是将学习任务转换为一个或多个单标签分类任务[7-8];第二类则在已有的单标签学习算法上进行改进,从而能适应多标签数据[9-10]。与标签互斥的单标签学习不同,多标签学习中的类标签之间通常存在相关性。例如,一个样本具有标签“骆驼”,则大概率也具有标签“沙漠”,而不太可能有标签“海洋”。有效利用标签相关性能提升算法的分类性能。根据标签相关性的利用情况,多标签学习算法又可分为一阶、二阶和高阶三类。一阶方法将多标签数据转换为多个互不相关的单标签数据,单独处理每个类别标签,完全不考虑标签相关性[4,11];二阶和高阶方法分别利用了标签对之间的相关性[12-14]和所有标签集或标签子集间的相关性[15-16]。

标签相关性一般通过分析训练样本获得,现有的大部分多标签学习算法默认观察到的标签矩阵是完整的。然而在实际应用中,随着数据量的急剧增长,主观的人工标注往往不能获取完整的标签信息,导致标签矩阵是不完备的。而不完备的标签信息会使得标签相关性的计算不准确,同时也会误导学习算法造成算法性能的下降。因此,提升不完备多标签学习算法性能的一个关键问题是在缺失标签情况下,如何正确地估算和利用标签相关性。

针对上述不完备多标签学习问题,目前已经提出一些基于标签相关性的分类方法。例如,文献[17]提出的基于边信息的加速矩阵补全算法和文献[18]提出的基于矩阵补全的多视角弱标签学习算法。两种算法都采用了同一种策略,即尝试将标签和特征空间组合成一个统一的空间,再使用标准的矩阵补全技术来补充缺失的标签,并且都利用了低秩结构来隐式地捕获标签相关性。然而,它们仅能在转导方式下适用,较大地限制了其应用。也有一些方法不使用转导学习的策略。比如,半监督不完备标签多标签学习算法[19]利用低秩矩阵恢复模型进行自动标签计算。但是,只有全局低秩标签结构被隐式捕获,而局部低秩结构被忽略。因此,为了同时考虑全局和局部的低秩结构,文献[20]提出缺失标签情况下的判别多标签学习算法,通过对具有相同标签实例的所有预测施加低秩结构算法,并对具有不同标签的实例预测施加最大分离结构,来完成对局部和全局低秩标签结构的建模。除了上述利用低秩结构来隐式地捕获标签相关性以提升算法性能的方法外,也有研究者直接显式地利用标签相关性矩阵。例如,文献[21]提出的缺失特征和标签情况下的多标签学习算法,不仅利用流形正则化技术保持了实例相似性和标签相关性,而且还利用矩阵分解理论来进行缺失标签的恢复。文献[22]提出基于特征-标签双映射的缺失标签-类属特征学习(FLDM)算法,利用标签向量直接计算标签相关性,并通过特征-标签双映射学习目标权重进行潜在的不完全标签恢复。然而,上述的标签相关性都是直接从训练数据中计算得到的,当训练数据中缺失大量的类标签时,标签相关性的计算结果会不准确。针对这个问题,文献[23]利用从不完整的训练数据中学习得到的标签相关性矩阵来进行缺失标签的恢复,提出了联合类属特征和标签相关性的缺失标签下的多标签学习(LSLC)算法。文献[24]通过建立辅助标签矩阵,对标签子空间施加低秩和高秩约束,并同时学习一个标签相关性矩阵来进行缺失标签的恢复和分类器的训练,提出基于低秩标签子空间变换的不完备多标签学习(LRMML)算法。此外,还可以在模型中加入实例相关性,以进一步提高模型性能。文献[25]提出的基于实例颗粒度判别的缺失标签情况下的弱多标签学习(C2ML)算法,能够同时利用实例流形和标签流形对标签流形进行重构训练特征标签映射,并进行分类器的学习和标签矩阵的恢复。然而,以上算法一般通过回归系数矩阵直接将数据从特征空间映射到标签空间,认为两个空间存在线性映射关系。但在多数情况下,这种线性回归假设是不合理的。

本文提出一种结合双流形映射的不完备多标签学习(ML-DMM)算法。该算法构造两种流形映射:特征流形映射保留实例的局部结构;标签流形映射捕获并利用标签的相关性。具体说来,ML-DMM首先由拉普拉斯映射[26]构造数据的低维流形,然后通过回归系数矩阵和标签相关性矩阵将初始特征空间和初始标签空间分别映射到该低维流形上,从而形成一种双流形映射结构来提升算法性能。最后利用迭代学习得到的回归系数矩阵进行多标签分类。

1 ML-DMM算法

在多标签学习中,由n个样本构成的训练数据集表示为X=[x1,x2,…,xn]T∈n×d,对应的逻辑型类标签集表示为Y=[y1,y2,…,yn]T∈{0,1}n×q,其中,d表示特征维数,q表示标签个数。样本xi∈d对应的逻辑标签为yi={yi1,yi2,…,yiq}∈{0,1}q,其中,1表示标签与实例相关,0表示标签与实例无关或标签缺失。

1.1 基于低维流形的回归模型

回归模型的目标函数一般形式如下:

(1)

受流形学习理论的启发,算法认为数据通过线性回归矩阵映射到数据的低维流形Z∈n×q,该数据空间和低维流形空间之间应具有相似的局部结构信息。具体地,若样本xi和xj在原始特征空间是相似的,则低维流形空间中对应的zi,：和zj,：也是相似的,其中zi,：和zj,：分别表示Z的第i行和第j行。因此,可以通过最小化流形正则化项来进行结构约束,Sij是邻接矩阵的第(i,j)项,表示实例xi和xj之间的相似度。当xi∈Nk(xi)orxj∈Nk(xj)时,邻接矩阵S计算如下:

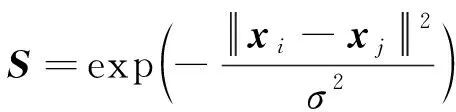
(2)

其中:σ是参数,通常设置为1;Nk(xi)表示实例xi的k近邻集合,本文中k值取为20。在其他情况下Sij=0。

因此,结合了低维流形Z的回归模型目标函数为:

(3)

1.2 双流形映射的构建

不完备的多标签数据使得一般多标签算法很难捕获正确的标签相关性。为了解决这个问题,ML-DMM定义了一个增广标签矩阵YC,其中,C∈q×q为标签相关性矩阵,每一个元素Cij表示第i个标签和第j个标签的相关性程度。与不完备的原始数据标签矩阵Y相比,增广标签矩阵YC通过标签相关性矩阵进行了扩充,从而拥有更丰富的标签信息。为了增强低维流形Z和增广标签分布之间的一致性,通过加入回归项来约束标签相关性矩阵。同时,这也形成了标签空间和流形空间之间的映射关系。结合式(3)中的回归项两者共同构成了一种双映射结构。因此,结合双流形映射的模型表示为:

(4)

其中:α1、α2和α3是权衡参数。

1.3 ML-DMM优化求解

式(4)的优化问题涉及3个优化参数Z、W和C。由于W的L1范数不具有光滑性,因此采用加速近端梯度[27]方法来优化目标函数。

1.3.1Z的更新

当W和C固定时,对Z求导并令导数等于0,得到封闭解:

(5)

其中:I是一个d×d的单位矩阵。

1.3.2W的更新

当Z和C固定时,目标函数仅为W的函数,被记为F(W),则W的计算如下:

(6)

其中:H是指希尔伯特空间。

f(W)和g(W)的定义如下:

(7)

(8)

QL(W,W(t))=f(W(t))+〔∇f(W(t)),W-W(t)〕+

(9)

(10)

(11)

(12)

其中:W(t)为W在第t次迭代的一个中间变量;Wt表示W在第t次迭代的结果;f(W)的导数为∇f(W)=XT(XW-Z);proxε(·)为元素软阈值运算符。

proxε(·)定义如下:

proxε(wij)=(|wij|-ε)+sign(wij)

(13)

1.3.3C的更新

当Z和W固定时,对C求导并令导数等于零,得到封闭解:

C=(α1YTY+2α3I)-1α1YTZ

(14)

其中:I是一个q×q的单位矩阵。

1.3.4 利普希茨常数计算

为了考察f(W)的利普希茨连续性,给定W1和W2,根据f(W)的导数∇f(W)可以推断:

(15)

其中:ΔW=W1-W2。

因此,目标函数的利普希茨常数计算为:

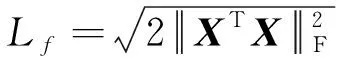
(16)

1.4 ML-DMM算法流程

算法1ML-DMM算法

输入训练数据集X,训练标签集Y,权重参数α1、α2、α3

输出回归系数矩阵W,标签相关性矩阵C,流形Z

1.初始化:构建拉普拉斯矩阵L;W0,W1←(XTX+λI)-1XTY;C←zeros(q,q);b0,b1←1;t←1;

2. 重复

3.根据式(16)计算利普希茨常数Lf;

4.根据式(5)更新Z;

7.W(t+1)←W(t);

9.根据式(14)更新C;

10.t←t+1;

11. 达到停止标准;

12. Z*←Zt;

13. W*←Wt;

14. C*←Ct;

1.5 ML-DMM算法复杂度分析

所提ML-DMM算法的时间复杂度可以从4个部分分别进行分析,即ML-DMM算法流程中步骤3的利普希茨常数Lf计算、步骤4的流形Z更新、步骤6的权重系数矩阵W更新和步骤9的标签相关性矩阵C更新。计算利普希茨常数的复杂度为O(nd2);更新Z的复杂度为O(nq2+ndq);更新W的复杂度为O(nd2+qd2+ndq);更新C的复杂度为O(nq2+q3)。因此,联合4个部分复杂度,ML-DMM的总时间复杂度为O(q3+(n+q)d2+nq2+ndq)。

2 实验

2.1 数据集

在8个多标签数据集上进行实验来验证所提算法的性能。所有数据集的详细信息如表1所示。

表1 实验数据集Table 1 Experimental datasets 单位:个

2.2 实验设置

本文的实验环境为Windows 10 64 bit操作系统,处理器为AMD Ryzen 7 5800H CPU,内存为16 GB。

为了验证所提算法的有效性,选取5种多标签学习算法与ML-DMM算法进行比较。ML-DMM算法的参数α1～α3在{2-8,2-9,…,22}中选取。5种对比算法及其参数设置分别为:1)LLSF[29]学习用于多标签分类的类属特征,参数α和β在{2-10,2-9,…,210}中选取;2)GLOCAL[30]利用全局和局部标签相关性来恢复缺失标签以进行多标签学习,参数λ=1,λ1～λ5在{10-5,10-4,…,101}中选取,k在{0.1q,0.2q,…,0.6q}中选取,g在{5,10,15,20}中选取;3)LSML[31]通过学习高阶标签相关性来补充不完整标签矩阵,将缺失标签矩阵恢复和类属特征学习统一到一个框架中,参数λ1～λ4在{10-5,10-4,…,103}中选取;4)FLDM[22]通过特征标签双映射进行潜在的缺失标签恢复,以有效地获得目标权重,参数α、β和γ在{2-4,2-2,…,213}中选取,参数λ设置为2-1;5)LRMML[24]通过建立辅助标签矩阵,对标签子空间施加低秩和高秩约束,从而进行缺失标签的恢复,参数δ设置为0.005,参数λR、λL和λT在{10-10,10-9,…,105}中选取。所有算法均通过网格搜索确定最优参数。

实验采用平均精度(AP)、平均ROC 曲线下面积(AUC)、1-错误率(OE)、排序损失(RL)[6]4种广泛使用的多标签学习评价指标来衡量算法性能。这4种评价指标的取值范围都为0～1,其中,AP和AUC的值越大,OE和RL的值越小,表示分类性能越好。

2.3 实验结果分析

实验将标签缺失率设置为10%、30%和50%,以此来比较训练标签矩阵不完备程度对算法性能的影响。同时,在每类标签中至少保留一个样本且每个样本至少保留一个正标签的前提下,根据预设的缺失率随机丢弃完整标签矩阵中的元素。所有实验都采用5倍交叉验证,并将5次运行的测试集性能指标进行平均,最终评价结果以平均值±标准差的形式呈现。

表2～表5展现了6种算法分别在3种缺失率和8个数据集上的性能指标。其中,↑和↓分别表示该指标值越大或越小,算法分类性能越好,ρ表示标签缺失率。表6进一步展现了不同算法在所有数据集的不同缺失率下各个评价指标的平均排序值。最优结果均以粗体表示。

表2 6种算法在AP (↑)上的实验结果Table 2 Experimental results of six algorithms on AP (↑)

表3 6种算法在AUC (↑)上的实验结果Table 3 Experimental results of six algorithms on AUC (↑)

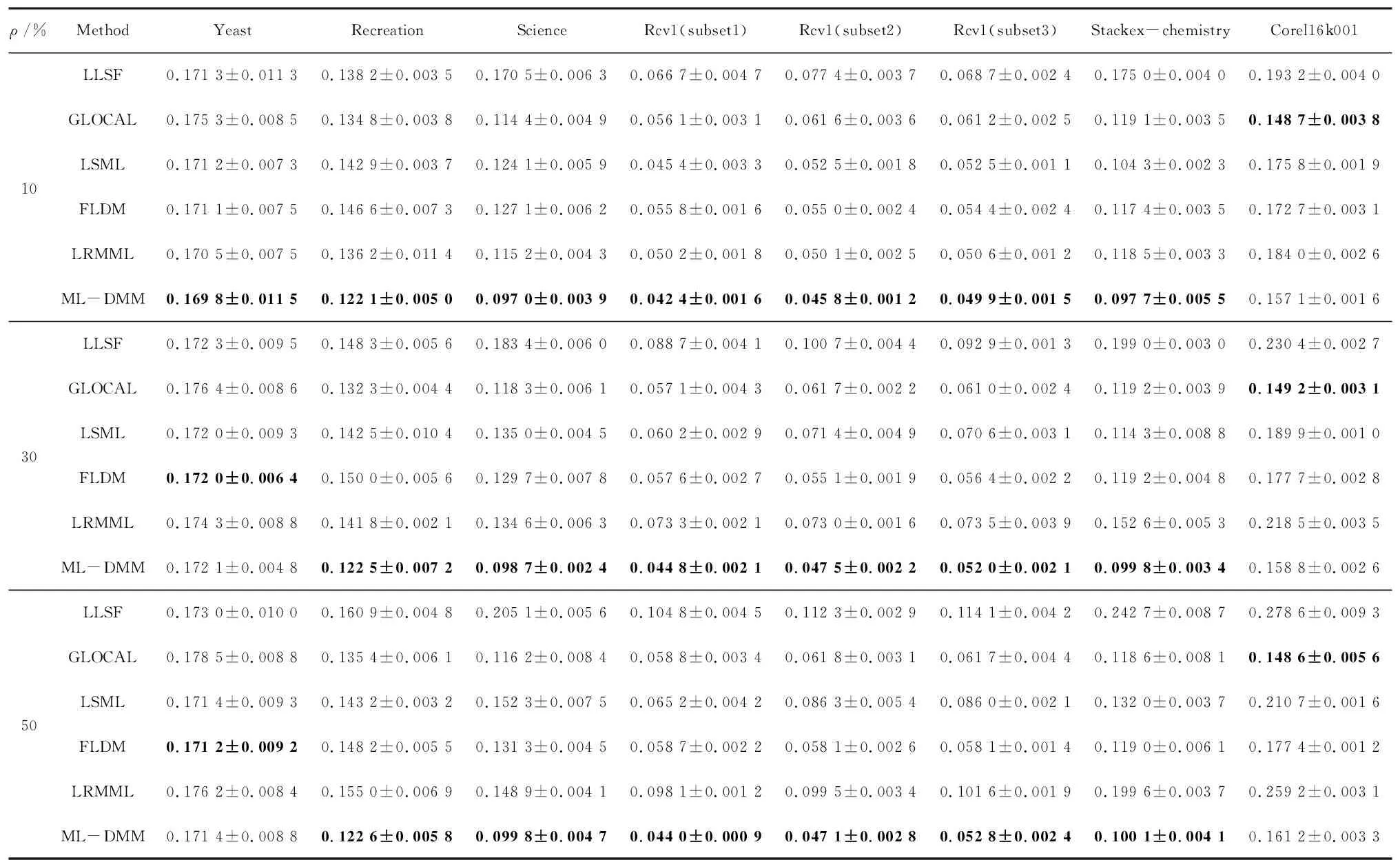
表5 6种算法在RL (↓)上的实验结果Table 5 Experimental results of six algorithms on RL(↓)

表6 不同算法在所有数据集上的平均排序值Table 6 Average ranking value of different algorithms on all datasets

从表2～表5的实验结果可以看出,随着标签缺失率的提高,所有算法的性能在不同数据集上都有不同程度的下降。这说明标签缺失越多,对算法性能的影响越大。其中,LLSF性能下降最多,明显劣于GLOCAL、LSML、FLDM、LRMML和ML-DMM。原因在于LLSF没有针对标签缺失的情况进行建模。而在其他5种算法中,虽然ML-DMM在数据集Yeast、Science和Corel6k001上未体现最优性能,但从总体上来看,其性能具有明显优势。原因在于算法的双流形映射不仅利用标签相关性矩阵扩充了缺失标签矩阵信息,还联合加强了流形空间、原始特征空间和原始标签空间之间的关联来提升分类性能。从表6的排序结果可以看出,ML-DMM算法在所有数据集上的平均排名是最高的。

在8个数据集上对于3种缺失率和4种评价指标,ML-DMM算法始终排名第一。

为评估6种算法的显著性差异,引入Nemenyi 检验[32]。当两种比较算法在所有数据集上的平均排名差异大于临界差异(CD)时,认为两种算法存在显著差异。CD计算公式如下:

(17)

其中:k为算法个数;N为数据集个数;qα为系数。置信度水平α=0.05,有6个算法和24个数据集(3种缺失率×8个多标签数据集),查表可得系数qα=2.850,从而计算得到临界差异为1.539 2。图1展现了每个评价指标对应的CD图,数轴表示算法的排名,即算法的性能在每个评估子图中从右到左依次下降。当两种算法性能没有显著性差异时用红色实线连接;反之,则无实线连接(彩色效果见《计算机工程》官网HTML版)。ML-DMM在每个子图中始终位于最右侧,这表明所提算法的性能排名是最高的。同时,ML-DMM在评价指标AUC和RL上显著优于其他算法,在AP和OE上与FLDM无显著性差异。实验结果和分析充分表明了ML-DMM在处理不完备多标签学习时的有效性。

图1 基于 Nemenyi 检验的算法性能比较Fig.1 Performance comparison of algorithms based on Nemenyi test

3 结束语

本文提出一种结合双流形映射的不完备多标签学习算法ML-DMM。该算法构造了特征流形映射和标签流形映射。前者用于保留实例的局部结构;后者用于捕获并利用标签的相关性。首先由拉普拉斯映射构造数据低维流形,然后通过回归系数矩阵和标签相关性矩阵将初始特征空间和初始标签空间分别映射到低维流形上,形成一种双流形映射的结构来联合加强流形空间、原始特征空间和原始标签空间之间的关联,提升算法性能。在不同标签缺失率下的多标签分类实验结果表明,相比于其他算法,ML-DMM具有更好的性能。ML-DMM算法通过迭代学习标签相关性矩阵,并将其用于不完备标签矩阵的增强,但未考虑标签相关性隐含的低秩结构特点。下一步将在标签相关性学习中有效利用其低秩性来提高不完备多标签学习性能。