线云隐私攻击算法的并行加速研究*
郭宸良,阎少宏,宗晨琪
(华北理工大学理学院,河北 唐山 063210)
1 引言
近年来,网络空间安全领域的隐私保护正面临着计算资源紧张和高实时性要求的双重挑战。在此背景下,多核并行计算和异构计算技术的快速发展,不仅为缓解这些问题提供了强大的算力支持,而且还推动了整个行业向绿色计算和低碳节能的可持续发展方向迈进。
针对线云的隐私攻击研究从传统基于照片的定位方法的隐私安全问题延伸而来。在基于照片的定位方法中,首先需要获取照片特征点,再通过求解n点透视PnP(Perspective-n-Point)等方法得到点云,最后通过ICP(Interative Closest Point)求解得到相机的运动姿态,这个过程也是视觉同时定位与地图构建SLAM(Simultaneous Localization And Mapping)或运动中恢复结构的内容之一。这种方法形成的点云实际是现实世界的特征点,携带了场景隐私信息。Pittaluga等[1]经过研究,设计了一种通过级联神经网络从尺度不变特征变换SIFT(Scale-Invariant Feature Transform)点云和特征描述子恢复原始场景图像的方法,指出传统基于点云的定位方法存在隐私安全隐患。这促使研究人员寻找新的具有隐私保护的定位方法,其中基于线云的定位方法被提出并逐渐得到关注。
线云是指空间中一组方向随机或按某种特定规律分布的直线。基于线云的定位方法最早是由Speciale等[2]提出的,该方法将点云中的点替换为经过该点的直线,这些直线的方向呈均匀分布,以此来隐匿原始点,避免了针对点云的隐私攻击。而根据Chelani等[3]的研究,这种方式仍存在缺陷:通过计算三维线云邻近线间最短距离点,能够得到近似点云,从而恢复出场景细节。该研究揭露了线云的隐私安全问题。
针对线云隐私安全问题的研究目前相对较少,形成的隐私攻击和保护算法较为单一。更多的是对算法理论可行性的关注,缺少性能研究,导致这些算法仍然需要大量时间进行实验,对后续研究较为不利。在线云隐私攻击算法的实验中,尽管该算法能够有效地恢复点云数据,但其处理过程常常受限于较长的等待时间,特别是在增加优化迭代次数以提高结果精度时,这一限制变得尤为突出。这是因为该算法没有经过并行优化,无法充分利用现代多核心中央处理器CPU(Central Processing Unit)的计算资源,而且计算过程中涉及大量的矩阵计算,未能调用图形处理器GPU(Graphics Processing Unit)进行加速处理。这给线云隐私安全研究工作带来了较多不便。
为此,本文针对线云隐私攻击算法计算时间开销大的问题展开研究,提出一种并行优化算法,采用CPU多核并行和图形处理器通用计算GPGPU(General-Purpose computing on Graphics Processing Units)并行方法,在个人计算机、高性能计算机和云服务器3个平台上,基于6个数据集测试其经过并行优化算法的性能和加速效果。实验结果表明,本文所提算法的计算性能得到了显著提升。
2 相关工作
本节主要介绍视觉SLAM方法、隐私保护的基于图像的定位方法、针对这种定位方法的线云隐私攻击算法以及当前主流并行化方法。
视觉SLAM方法最早是由Se等[4]在2002年提出的,该方法利用相机图像实现定位和建图,被广泛应用于机器人、自动驾驶和扩展现实等领域。尽管具有较低的传感器需求和支持实现物体识别等优点[5],但其涉及的隐私保护问题也逐渐引起关注。2019年Pittaluga等[1]提出从三维点云还原场景图像的方法,之后Speciale等[2]提出了基于图像的隐私保护定位方法,引入了线云的概念。
然而,Chelani等[3]发现这种基于线云的定位方法依然存在安全隐患,提出了一种基于密度的线云隐私攻击算法。该算法采用串行策略,效率较低。为了解决这个问题,并行化改进原算法将成为关键。
并行计算可以大幅提升算法效率,实现程序高效运行。在这种背景下,本文将研究并行计算在解决线云隐私攻击问题上的应用。根据Li等[6]的总结,当前的并行程序可以分为主/从模式、单程序多数据SPMD(Single Program Multiple Data)模式、数据流水模式、分治模式、推测多线程模式和混合模式6种模式。计算机视觉任务一般是计算密集型,可以采用这些模式来提高并行度,降低时间开销。另外,计算机视觉任务的并行化处理可分为高、中、低3个层次[7]。高层次视觉任务往往采用基于数据的并行方法,如Chen等[8]提出的Eyeriss架构和Hanif等[9]提出的大规模并行神经阵列MPNA(Massively-Parallel Neural Array)架构;中层次的计算机视觉任务,如区域分割、运动分析和三维重建,其并行化方法往往需要有针对性的改进,如Wu等[10]和Rodriguez-Losada等[11]在GPU上实现的集束调整和ICP求解算法。低层次的计算机视觉任务,如平滑化、直方图生成、聚类等,现有系统就可以并行完成这些任务[12]。
对于线云隐私攻击算法的并行优化问题,可以结合上述并行计算模式和层次进行设计。后续将详细讨论如何具体应用这些方法。
3 线云隐私攻击算法原理
本节主要介绍基于密度的线云隐私攻击算法的原理,并按照求线云邻近区域、求极值和结果优化3个步骤进行阐述,之后分析这3个步骤的时间复杂度并找出最耗时的步骤,最后对其进行并行化改进分析。
考虑在空间中的一个点,当将其扩展为一条线时,线上各个点的概率密度呈均匀分布,这有助于隐藏原始点的位置。然而,在考虑点云时,这些点在空间中的分布存在密度差异,即使将它们扩展为线,密度信息仍然保留。通过找到这些线之间的最近点,可以较好地估计原始点的位置,并还原原始点云。
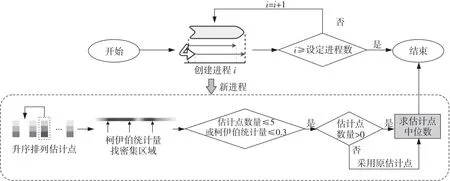
上述过程整体流程如图1所示[3]。该流程主要将点云恢复任务分为3个步骤:(1)根据线云中的任意2线间距离,求出每条线的邻近区域。(2)根据找出的邻近区域和邻近点,通过求极值的方式找出位于最大重叠密度区域的邻近点,并将其作为备选点来恢复点云。(3)在初次粗还原出点云后,先通过求交集的方式排除穿过邻近区域而不包含邻近点的线;再按照步骤(1)和步骤(2)求点云,得到更优的结果;不断循环该步骤,直到达到设定的优化次数。
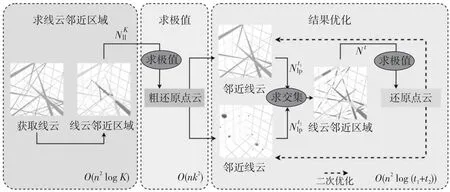
Figure 1 Process and time complexity of density-based line cloud privacy attack algorithm

(1)
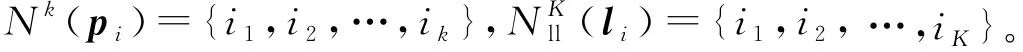
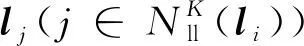
(2)
其中,vi为线li的方向向量。
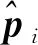
(3)
其中,当βij<β时,Iβij<β=1,否则Iβij<β=0。
柯伊伯统计量KS(Kuiper Static)则定义如式(4)~式(6)所示:
(4)
(5)
(6)
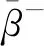
(7)
其中,N(li)为排除穿过线li的邻近区域且不包含邻近点的线的索引集合。将所得的线继续按照步骤(1)和步骤(2)的做法还原点云,并循环至设定次数。
下面分析该算法的时间复杂度。步骤(1)中,假设要处理的线云数据集S中有n条线(对应n个点),在求线云中任意2线最小欧氏距离集合dll时,采用穷举法进行计算的时间复杂度为O(n2);而为了得到线云中所有线各自最近的K条线,采用堆排序的时间复杂度为O(n2logK)。因此,该步骤总的时间复杂度为O(n2logK)。步骤(2)中,求n条线上的k个邻近区域的极值点,时间复杂度为O(nk2)。步骤(3)中,根据还原点云求邻近线和根据线云求邻近点,时间复杂度分别为O(n2logt1)和O(n2logt2);求每条线上t1个邻近点以及对应的t2个邻近线的交集,时间复杂度为O(n(t1+t2))。因此,该步骤总的时间复杂度为O(n2log (t1+t2))。
在考虑并行优化时,这3步中后2步分别需要上一步的结果,因此整体上它们应该串行执行。每个步骤内部不存在先后顺序,所以并行优化应在每个步骤内部进行。步骤(1)和步骤(3)的数据容易拆分且主要涉及矩阵计算,可以采用CPU和GPU处理。而对于步骤(2),其时间复杂度相对较低;且每条线上的待选点在求交集后数量彼此不一定相等,这种不平衡的数据将难以直接交给GPU进行并行计算。另外,该步骤计算包含较多跳转指令,更适合直接交由CPU处理。因此,步骤(2)的并行优化应该考虑采用CPU并行。
4 CPU多核并行实现
本节主要介绍基于CPU的并行化线云隐私攻击算法和对应的数据拆分方法,并讨论该并行化算法的局限性,分别从多进程求邻近区域和多进程求邻近区域极值点2方面进行阐述。
为了减少原算法在实际计算时的时间开销,需要对其进行并行化改进,尤其是对时间复杂度较高的部分。CPU多核并行可以采用多线程方法和多进程方式。在具体实现上,部分编程语言,如Python,受限于全局解释器锁GIL(Global Interpreter Lock),多线程算法无法充分利用计算机多核心CPU的计算资源[13],因此采用多进程算法具有更好的通用性。采用SPMD模式,通过创建多个进程实体,对线云隐私攻击算法进行并行化改进,以实现在诸如求线线间欧氏距离、寻找邻近点、求邻近区域极值点等CPU密集型任务中得到较高的加速比。
4.1 多进程实现流程
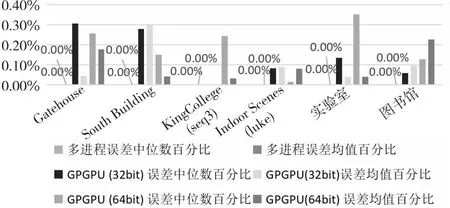
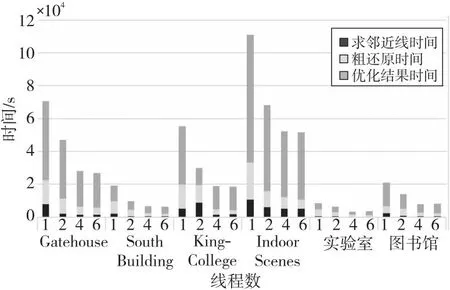
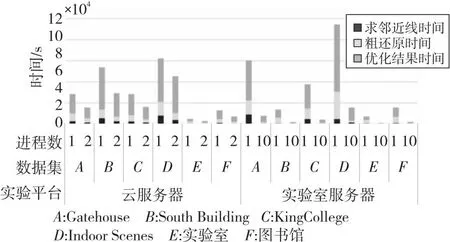
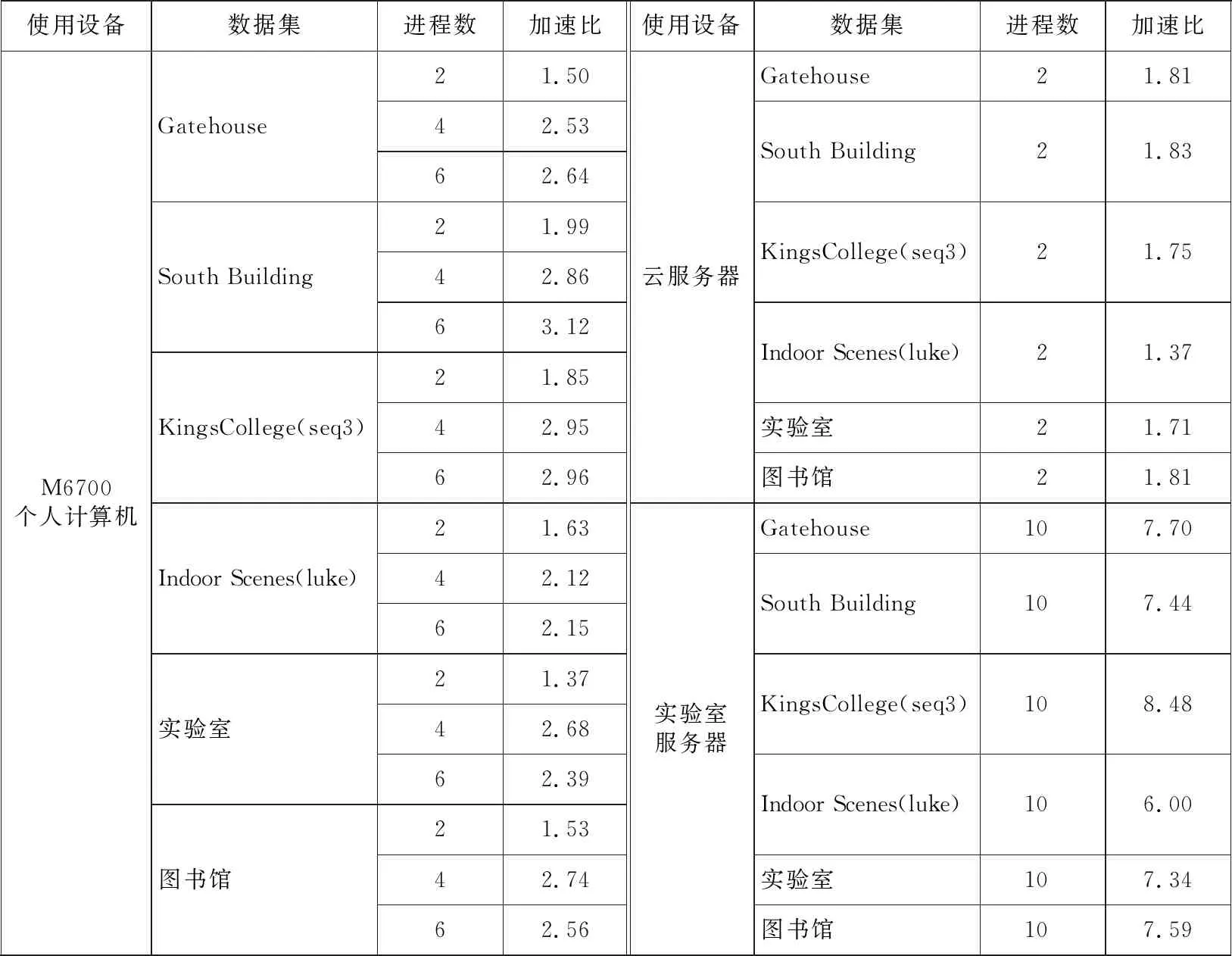
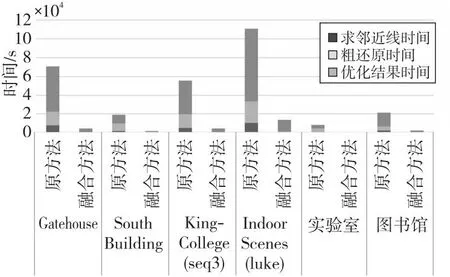
由于多进程间通信存在额外开销,为了减少这种开销,划分每个进程任务后不再调整任务量,直到该进程结束。分别将线云隐私攻击算法的3个步骤进行并行化改进。设其总任务量分别为N1,N2和N3,将其分为t组,分配到对应t个进程中,每个进程的任务量为N1/t,N2/t和N3/t。由于创建新进程存在额外开销,因此即使每个进程任务量相同且分配到相同规格的CPU核心,其结束时间也存在先后差异,造成并行度下降。为了进一步减少这种差异,当多出的任务量n 上述过程如图2所示。第1步,求邻近区域需要计算得出线云中任意2条线间的距离并取最近的k条线,速度最快。第2步,粗还原中对所有待选区域求其极值点,未排除偏差较大的区域,其还原效果较差,时间成本也较高。第3步,迭代求临近区域极值点,由于需要迭代优化结果,速度最慢,其并行程度将直接影响整体的加速比,因此应重点关注该部分。其中,求交集步骤时间复杂度相对较低,实际运行中原算法速度已经足够快,并行化改进效果提升较小,甚至可能导致运行时间延长,因此这个部分依然采用原算法。 Figure 2 Timing diagram of CPU parallelized linecloud privacy attack 下面介绍求邻近区域的多进程改进部分。在该过程中首先需要计算出线云中任意2条线间的距离,之后继续求出其邻近的k条线,这可以通过对每条线和其余线的距离进行排序得到。 Figure 3 Splitting process of CPU multi-process data 该过程可以表示为算法1。 算法1 CPU多进程求邻近区域算法输入:线云Lines,线条数Count,进程数t。输出:邻近点Neighbors。1.function RunProcess_i(lindex,rindex,value1,value2):2. for i=lindex→rindex do3. for j=0→Countdo4. dst[i][j]=GetDistance(value1[i],value2[j]);5. end for6. Neighbors[i]=GetNeighbor(value1[i],dst[i]);7. end for8. return Neighbors;9.end function10.p=CreateProcess(t);11.bulk_size=Count/t+1;12.for i=0→t-1 do13. p[i]=RunProcess_i (bulk_size×i,bulk_size×(i+1)-1,Lines,Lines);14.end for15.p[t-1]=RunProcess_i (bulk_size×(t-1),Count-1,Lines,Lines);16.依次启动进程p并等待结果; 至此,线云中每条线的邻近区域已经求出,下一步将通过求线上概率分布函数极值点的方式求估计点。 在求邻近区域极值点之前,需要先去除穿过邻近区域而非邻近点的线。可以先求得距离估计点最近的k条线和距离目标线最近的k个点,然后取交集。该过程也可以并行化处理。首先,分别以估计点和目标线为基准求其到其他线的距离。具体来说,每个进程的任务中,采用算法1中的RunProcess_i函数,其value1和value2分别为线和估计点,求出估计点的邻近线;然后交换value1和value2的值,得到目标线的邻近点;最后再取其交集,得到筛选后的邻近区域。 然后,根据设定的进程数量依次启动各进程,按照算法1中的方法分配对应任务数量。各进程执行过程中,首先按距离升序排列待筛选估计点;之后根据式(2)和式(3)求邻近区域的概率分布函数及柯伊伯统计量,并循环执行该步骤直到筛选后的估计点数不大于5个或柯伊伯统计量不大于0.3[3];最后将多个估计点距离的中值作为最终估计点,从而得到概率密度极大值点。该过程如图4所示。 Figure 4 Flow chart of getting peak in neighbors using CPU multi-process Figure 5 Parallelized linecloud privacy attack timing diagrm of GPGPU 至此,CPU多进程的并行改进算法已得到所求点云,可以进一步采用文献[1]中的方法还原场景图像。 多进程并行算法在创建新的进程和进程间通信等方面相比多线程算法会产生更多的开销,因此这种算法总体上性能不如多线程算法,但对于现代具有较多核心的计算机来说这种开销是可以接受的。另外,采用CPU多核并行可以实现线性的性能提升。但是,随着数据量的增加,CPU性能增速往往已经不能满足需求,此时应该考虑采用其他计算机架构进行加速计算。GPGPU的出现为解决大规模矩阵计算问题提供了新思路,下面将介绍该并行化算法。 本节的内容结构与上一节的类似,主要介绍GPGPU并行化线云隐私攻击算法、对应的数据拆分方式以及该并行化算法的局限性,重点对并行求邻近区域部分进行阐述。 在原算法中,求线线间欧氏距离和寻找邻近点的任务都需要进行大量的矩阵计算,而传统的基于CPU的程序在执行这些任务时效率不高。为了充分利用现代计算机的计算资源以实现更好的效果,采用GPU进行处理。这是因为,GPU内部配备大量的流处理器,可以高效并行求解,从而提高速度。因此,采用GPGPU的方式并行化改进原算法是非常合适的。然而,对于那些数据不平衡、包含不确定计算结果且计算资源消耗相对较少的任务,如邻近区域求极值点,采用GPU难以达到理想的加速效果,因此仍然采用CPU进行计算。对于适合进行GPU并行改进的部分,根据GPU的计算原理,在设计算法时应增加单次计算的数据量,从而减少循环。为此,将原有的二维数组转为三维数组,在单次计算中同时得到一组结果,这样更适合GPU进行数据处理。利用飞桨框架的GPU计算平台,采用数据流水模式,通过创建CPU和GPU线程,分别执行对应的任务。对于所含线条数为Count的数据集,设GPU线程和CPU线程处理一轮数据的时间分别为s1和s2,共处理R轮。当s1>s2时,总运行时间为R×s1+s2,如图5中上半部分所示;当s1≤s2时,总运行时间为s1+R×s2,如图5中下半部分所示。 Figure 6 Splitting process of GPGPU data 然而,在求邻近区步骤中,GPU在面对具有大量判断和跳转命令的程序时性能表现不佳[14],因此这部分任务依然采用CPU处理。同时,为了进一步提高并行度,采用多线程算法,使CPU处理本轮数据时GPU能继续处理下一轮数据。这样就形成了一种数据流水模式,充分利用了CPU和GPU的并行处理能力,提高了整个过程的计算效率。首先,使用2个临界区互斥信号量SemaphoreGPU和SemaphoreCPU,分别用于控制GPU线程和CPU线程的访问。然后,通过创建2个线程来实现GPU和CPU的并行计算。GPU线程负责计算线与线之间的距离,而CPU线程则负责查找最近的线。在GPU线程中,通过锁住SemaphoreGPU来确保GPU邻界区的互斥访问,然后进行线与线距离的计算,并释放SemaphoreCPU。在CPU线程中,通过锁住SemaphoreCPU来确保CPU邻界区的互斥访问,然后进行最近线的查找,并在完成后释放SemaphoreGPU。这个过程如算法2所示。 算法2 GPGPU求邻近区域算法输入:线云Lines,线条数Count,GPU单次输入数据大小Size。输出:邻近点Neighbors。1.SemaphoreGPU=1;2.SemaphoreCPU=0;3.round=(Count+1)/Size+1;4.function RunGPUThread(value1,value2):5. for i=0→rounddo6. dst_tmp=GetDistance(value1[Size×i:Size×(i+1)],value2);7. P(SemaphoreGPU);8. dst=dst_tmp;9. V(SemaphoreCPU);10. end for11.end function12.function RunCPUThread(value):13. fori=0→round do14. P(SemaphoreCPU);15. Neighbors[Size×i:Size×(i+1)]=GetNeigh-bor(value[Size×i:Size×(i+1)],dst);16. V(SemaphoreGPU);17. end for18.end function19.扩充Lines到Size×round行,填充零值20.StartThread(RunGPUThread(Lines,Lines));21.StartThread(RunCPUThread(Lines));22.等待线程结果并得到结果Neighbors[0:Count] 在实现GPGPU算法时,优化访存模式是提高性能和效率的关键手段之一。通过合理管理数据的读取和写入操作,并充分利用GPU的显存存储结构,可以减少访存延迟并提高数据访问速度。本文算法主要采用数据重用来进行优化。 对于经常需要重复使用的数据,如线云Lines,可以将其传输到GPU后一直存储在显存中,直到所有组计算结束。当使用单精度浮点数且数量为十万时,其所占用的显存空间约为2.29 MB,这是完全可接受的。此外,由于在数据拆分过程中按照顺序分组,数组采用顺序存储,在同一组计算过程中不同流处理器访存地址接近,具有较好的空间局部性,其访存时间也比较接近,具有较好的时间局部性,所以通过利用一级缓存和二级缓存,可以减少对全局存储器的访存流量,降低访存时间。另外,在GPU计算过程中生成的一些中间值数组如矩阵叉乘结果NS,其大小为3×Size×Count,对于数量为十万大小的线云,取Size为2 000时,占用显存2.2 GB,如果每次循环都要重新创建,将花费较多时间。事实上,在前R′-1组循环中它们的大小和维度保持不变,可以重复利用,无需重新开辟显存空间。最后,在CPU单核性能尚未达到瓶颈且显存充足的情况下,应尽量增加Size的大小,以减少GPU对内存的访存次数,使GPU访问显存的时间更长。 虽然采用GPU进行处理相比采用CPU具有许多优势,但也存在一些局限性需要考虑。首先,与CPU处理不同,GPU处理需要将数据从内存转移到显存,并根据GPU硬件的具体支持情况调整数据精度,例如,从双精度降至单精度浮点数。因此,在实际应用中,需要通过实验对数据转换引起的结果差异进行测量和评估,以确保最终结果的准确性。 其次,GPU在计算过程中主要负责计算任务,如求线线距离,而CPU任务较为有限,主要为数据转换和转移。此外,实际实验中不同型号的CPU和GPU之间性能也存在差异,导致两者负载并不均衡,降低了算法的并行度。为了解决这个问题,可以采用CPU多进程和GPGPU融合的计算方式。具体而言,对于多核CPU,当其单核性能较弱时,GPU的数据填充速率较低,导致吞吐率较低。这时,可以增加额外的GPGPU计算进程,利用多个进程向GPU发送任务,以提高GPU的利用率。由于这些GPGPU进程优先级一致,为了使其在相近的时间点结束,其任务量也应保持一致。CPU在运行GPGPU进程后,若仍有空闲时间可用,为了进一步利用这些空余资源,可以根据第3节的方法增加CPU计算进程。为了确定最佳任务分配策略,需要通过实验进行测定。 在接下来的实验中,将对上述算法进行测试,以评估并行算法的实际效果。 本文实验分别在包含室内、室外场景的不同数据集上进行测试。首先对于数据集中的原始图像利用colmap得到点云;然后对比原算法、CPU多核并行优化算法和GPGPU优化算法在处理相同数据集时的精度和性能差异;最后结合CPU多核并行算法和GPGPU优化算法实现异构计算,以得到最佳性能。 为了在更广泛的硬件平台测试本文算法的加速效果,本文实验在3个具有代表性的平台上展开:代表低功耗的个人笔记本电脑M6700(配备i7-3740QM的4核心CPU和Quadro®P4000的GPU)、具有多CPU核心的HPC的实验室服务器(配备Xeon®E5-2680 v4的14核心CPU)和配备更强CPU和GPU的云服务器(配备Xeon®Gold 6148的虚拟化双核心CPU和Tesla®V100的GPU)。采用4个公开数据集(Gatehouse[15]、South Building[16]、KingsCollege[17]和Indoor Screens(luke)[18,19])和2个私有数据集(实验室、图书馆),共包含2个室内场景和4个室外场景,室外场景中包含3个地面拍摄场景和1个航拍场景,具有不同的尺度大小和点云密度分布情况,能够较为全面地测试算法攻击效果。通过对比在不同平台上的计算时间和效率来验证本文并行算法的实际效果。各数据集为图像序列,为了从图像序列获取点云,采用colmap3.5(CUDA®)自动模式进行重建,质量选择为“高”,生成txt格式的点云数据并输入到实验程序中。 精度测试主要验证所提并行优化算法的正确性,以确保其不会改变原算法的结果。在本节实验中,由于GPGPU计算方式中采用32位和64位浮点数时精度不同,且运行速度有较大差异,因此需要分别考虑这2种方式。本节实验环境为M6700个人计算机,设定迭代次数为2,得到的线云还原的点云相对原算法的误差百分比如图7所示。 Figure 7 Bar chart of relative error percentage of different algorithms 由图7可知,CPU多进程并行优化算法和原方法误差百分比都为0,表明基于CPU的多进程并行优化算法不影响算法结果;而GPGPU算法的误差百分比都在0.4%以内,对结果的影响极小,且在实验中,采用32位时相比采用64位的具有更高的运行速度和更低的显存占用。综上,本文实验采用32位浮点数表示进行GPGPU计算,因为其在运行速度和显存占用方面具有更高的性能。 本节实验利用Python中multiprocessing库进行并行加速,在M6700个人计算机、云服务器和实验室服务器上对多种数据类型进行测试。实验结果如图8和图9所示。 Figure 8 Programs running time of M6700 personal computer under multi-process Figure 9 Program running time of cloud server and laboratory server under multi-process 从图8和图9可以看出,在不同平台上,随着进程数的增加,算法执行时间明显缩短,相比单进程的加速比情况如表1所示。从表1可以看出,在M6700个人计算机上从1个进程增加到6个进程时,加速比增速逐渐放缓,受限于物理核心数,在进程数超过4后,继续增加进程数量对于程序性能的提高逐渐变得缓慢,总体来说,性能还是不断提高,计算时间不断减少,加速比最高达到3.12;而对于拥有更多物理核心的实验室服务器,可以进一步增加进程数,在10个进程时达到的最高加速比为8.48,加速效果明显。 Table 1 Program speedup ratio under multi-process 根据具体硬件条件合理设定GPU的数据量。在本文实验中,对于80 000条线组成的线云,当取Size为5 000时,可使显存占用率达到80%以上,效果较好,实验结果如图10所示。从图10可以看出,在不同平台上采用GPU方式计算,算法的执行时间明显缩短,相比原程序的加速比情况如表2所示。 Table 2 Program speedup ratio under GPGPU表2 GPGPU下程序加速比 Figure 10 Program running time of each dataset under GPGPU 经过多组实验可知,以Gatehouse数据为例,经过GPU加速,运行时间大大缩短,相比原程序,其最大加速比为13.70,加速效果显著。 本节实验将CPU多进程并行和GPU并行算法结合起来,共同完成从线云恢复点云的任务,从而充分利用计算资源。具体实现上,将原数据集进行拆分,分别输入到CPU进程和GPU进程,从而获得最优性能。如图11和表3所示是在M6700个人计算机上,在求邻近线、粗还原和优化结果3个任务中CPU和GPU任务量分配比分别为:0∶1,1∶60和1∶4,且CPU进程数设置为4时,达到最佳时间和加速比。 Table 3 Program speedup ratio of fusion algorithm Figure 11 Program speedup ratio of fusion algorithm 可以看到,经过多组实验,经过融合后算法的最大加速比达到了15.11,相比单独采用CPU并行化算法的提高了472.35%,相比单独采用GPGPU算法的提高了10.29%,具有明显的提升效果。 在进行融合算法实验时,针对不同数据集以及不同计算平台,CPU和GPU任务量的分配将对总时间产生较大影响。由于GPGPU方式往往比CPU方式更快,所以应向GPU分配更多任务量,而当不同计算方式之间加速比差距过大时,如在求邻近线任务中CPU并行加速比为5左右,而GPGPU则达到了25左右,此时应只采用GPGPU方式。另外,由于GPGPU计算方式仍然需要CPU参与,因此,在实际中应考虑为其留出足够的CPU计算资源,减少抢占CPU需要的等待时间,从而使总吞吐量达到更高值。 本文实验的重点在于测试并行优化和异构计算优化对线云隐私攻击算法的加速效果。实验结果表明,通过并行优化和异构计算优化,能够在较低的时间成本下获得较好的攻击效果。 通过对线云隐私攻击算法进行并行化处理,可以解决其速度过慢的问题。利用多进程拆解恢复任务,并通过不同的CPU和GPU核心进行计算,对原算法进行改进,并且在多个平台和不同数据集上进行实验。结果表明,该并行算法能够快速地得到估计点并对结果进行优化,大幅度减少了计算时间,与原有算法相比加速效果明显,且对结果影响较小。融合CPU和GPU计算的实验结果进一步降低了总时间开销,充分利用了现代配备多核心处理器和GPU的计算机的计算资源,进一步缩短了等待时间。对于类似包含大量矩阵计算的问题,融合算法的实验结果为其性能优化提供了有益参考。在未来的工作中,可以针对算法的空间复杂度问题进行改进,并通过缩短GPU等待延迟和提高吞吐量来进一步提高并行效率。此外,针对GPU的Top-K算法优化也是一个值得深入研究的问题。该算法直接影响GPU求邻近区域的任务,通过优化该算法,可以使该任务受益,并进一步提高整体性能。
4.2 多进程求邻近区域



4.3 多进程求邻近区域极值点

4.4 局限性
5 GPGPU并行实现
5.1 GPGPU实现流程
5.2 GPGPU求邻近区域



5.3 GPGPU的访存优化
5.4 局限性
6 实验与结果分析
6.1 实验环境及数据集
6.2 并行优化算法的精度测试及分析
6.3 CPU多进程并行实验结果及分析
6.4 GPU加速实验结果及分析


6.5 融合CPU与GPU算法实验结果及分析

6.6 实验总结
7 结束语

